计及静态电压稳定约束的最少发电机优化调度方法

邓晓帆，王 蕾，刘建涛，郑春旭

（1.山东理工大学 电气与电子工程学院，山东 淄博 255000；2.国网淄博供电公司，山东 淄博 255000）

0 引言

作为电力系统电压稳定预防和校正控制的有效措施之一［1］，发电机优化调度在提高静态电压稳定性方面应用广泛［2］。在紧急运行状态下，即电力系统的稳定裕度较小时，运行人员更关注如何能在尽可能短的时间内实施最少数量的控制措施，及时调整系统运行状态，预防系统潜在危险。

对于最少控制数量的求解问题，通常有2 类处理方法。第1 类处理方法是通过限制最大控制设备数量／操作次数的方式，即规定离散变量的最大值，将该条件作为约束计入问题模型，再采用优化的方法进行求解。文献［3］将一天中有载调压变压器档位限制、可调发电机的数量以及可投切电容器的组数作为不等式约束纳入无功优化模型进行求解；文献［4］考虑有功出力调整发电机的最大数量，求解基于直流潮流的发电成本最小的优化问题；文献［5］将发电机有功出力和机端电压作为离散控制变量，求解包含离散变量最大动作次数约束的电压越限校正问题。第2 类处理方法是先将离散变量用连续函数表示，求解后再进行取整处理。文献［6］将可投切电容器组数和变压器分接头档位连续化，得到不考虑设备动作次数的理想化曲线，再通过前推-回推式动态算法阶梯化理想曲线，求解考虑控制设备最大动作次数的整数解；文献［7］将模型中包含最大调整次数限制的无功补偿设备、变压器等离散变量不等式约束松弛为连续变量等式约束，采用内点法求解无功优化问题，再结合分支定界法进行整数逼近，优化结果使网络损耗明显降低。

最少控制数量问题包括确定需要调整的设备及具体调整量大小，这类问题在数学上被描述为混合整数非线性规划（mixed integer nonlinear programming，MINLP）问题。为降低大规模电力系统MINLP 问题的求解难度，目前常见的求解方法主要包括Benders 方法［8］、灵敏度方法［9］等。文献［10］利用交替方向乘子法将交流潮流约束下的机组组合模型解耦为2 个子问题进行交替求解，兼顾了求解速度与精度；文献［11］利用灵敏度函数将交流潮流等式／不等式约束转化为线性约束，将原MINLP 模型转化为混合整数线性规划（mixed integer linear programming，MILP）模型，求解效率大幅提高。此外，为提升这类问题的求解速度，部分学者在求解原问题之前增加一个预筛选阶段，可在一定程度上缩小最优解的搜索空间。针对传统负荷削减问题的求解时间无法满足在线评估时效性需求的问题：文献［12］利用各支路功率对母线节点的灵敏度筛选负荷削减范围，将全局寻优转换为局部寻优，显著缩短了模型求解时间；文献［13］将线路开断对节点电压变化量的影响因子作为筛选指标，生成有效的线路开断候选列表供后续模型求解，满足了在线应用时效性需求。

本文主要研究如何通过调整最少的发电机数量提升电力系统的静态电压稳定性，所建模型为典型的非确定性多项式（non-deterministic polynomial，NP）-hard问题［14］，模型的主要求解难点包括：无功平衡直接影响电力系统的电压稳定性，因此模型无法采用PQ 解耦方法和线性化的直流潮流模型进行求解；模型中不仅存在潮流平衡等大量非线性约束，还存在表征发电机状态的离散变量和表征控制量的连续变量，这导致原问题求解难度大幅增加。为提高模型求解效率，本文提出含快速筛选和模型转化的阶段式求解方法。首先，利用快速筛选减少下一阶段模型求解中的无效控制变量并提供初始解；然后，基于可行性泵（feasibility pump，FP）算法［15］将原问题转化为2个子问题进行交替求解，子问题1为一个MILP 问题，用于快速确定需要调整出力的发电机，子问题2为一个非线性规划（nonlinear programming，NLP）问题，用于计算发电机有功出力的具体调整量；最后，对本文所提模型和求解方法进行算例仿真，与分支定界（branch and bound，B & B）法的对比结果验证了本文所提方法在计算精度和速度上的优势及其在大规模电力系统中在线应用的潜力。

1 计及电压稳定约束的最少控制数量模型

1.1 目标函数

本文以最少的发电机调整数量为目标函数，如式（1）所示。

式中：si为表征节点i处发电机是否参与有功出力调整的离散变量，若该发电机参与出力调整，则si=1，否则si=0；ng为系统中发电机的总数量。

1.2 约束条件

1）连续潮流平衡约束。

任一节点i应满足连续潮流平衡约束，即：

2）功率平衡约束。

发电机出力调整后，任一节点i应满足功率平衡约束，即：

式中：Vi、Vj分别为在潮流运行点处节点i、j的电压幅值；θij为在潮流运行点处节点i与节点j间的电压相角差。

3）发电机有功出力调整约束。

为保证系统功率平衡，同时减轻平衡机负担，系统中参与调整的发电机出力调整量总和应满足：

调整后发电机有功出力应满足发电机运行约束，即：

4）静态电压稳定裕度提升需求约束。

优化调整后系统的负荷裕度应满足运行人员的需求，即：

式中：λpost为优化后系统的负荷裕度；λbase为基态系统的负荷裕度；α为运行人员期望负荷裕度提升的比例，其值可根据当前系统的λbase确定。

5）安全运行约束。

发电机出力调整后，电力系统潮流运行点处的节点电压和支路功率应当满足安全运行约束，如式（7）—（9）所示。

本文负荷模型采用综合模型的静态模型，即ZIP模型，如式（10）所示。

式中：Vi0为节点i的参考电压；Pi0、Qi0分别为节点i处负荷在参考电压Vi0下的有功和无功需求；ap、bp、cp分别为恒阻抗、恒电流、恒功率负荷的有功功率占总有功功率的比例，且ap+bp+cp=1；aq、bq、cq分别为恒阻抗、恒电流、恒功率负荷的无功功率占总无功功率的比例，且aq+bq+cq=1。在实际电力系统中，恒阻抗、恒电流、恒功率负荷的占比大小与实际负荷的性质有关。

2 阶段式求解方法

第1 章的模型旨在当电力系统电压稳定裕度不足时，通过调整最少数量的发电机有功出力提升电力系统的负荷裕度。对于大规模的电力系统而言，系统中发电机数量众多，这会导致维数灾问题。此外，MINLP 问题的经典求解方法 —— B & B法无法满足时效性需求。为了提高可行解的求解速度与质量，本文提出一种阶段式求解方法，该方法包括快速筛选和模型转化2 个阶段。该方法按照候选设备数量逐渐减少、求解模型逐渐精确的思路展开，避免了对MINLP 问题的直接求解，达到了缩短计算时间以及保证求解质量的目的。

2.1 阶段Ⅰ：基于灵敏度的快速筛选

为了能够从众多的发电机中快速识别出对提升电力系统负荷裕度有效的发电机，快速评估发电机出力调整后电力系统负荷裕度的变化量，本文首先利用负荷裕度对发电机有功出力的灵敏度对有效发电机进行分类和筛选。

将连续潮流平衡方程式（2）列写为参数化的紧凑形式，即：

式中：f(x，u，λ)为关于x、u、λ的连续潮流平衡等式约束，x为系统状态变量（即节点电压幅值和相角），u为控制变量（本文中为发电机有功出力PGi）。

在鞍结分岔点（saddle-node bifurcation，SNB），式（11）的一阶泰勒展开式可表示为：

式中：Δx、Δu、Δλ分别为系统状态变量、控制变量、负荷裕度的增量。由于系统雅可比矩阵在SNB处奇异［16］，因此存在1 个对应雅可比矩阵的零特征值的非零左特征向量ω使得ω(∂f/∂x)=0。SNB 处系统负荷裕度λ对控制变量u的灵敏度为：

2.2 阶段Ⅱ：基于FP算法的数学模型转化

在阶段Ⅱ，利用FP 算法从阶段Ⅰ的候选集合中寻找出最少调整数量的发电机，并计算其有功出力具体调整量。

本文所提问题的数学模型可列写为如下紧凑形式：

式中：m为在阶段Ⅰ剔除的发电机数量；F(x，u，λ)为关于x、u、λ的所有等式约束；g(x，u，λ)为关于x、u、λ的不等式约束；分别为节点i处发电机有功出力调整量上、下限；为节点i处发电机有功出力当前值。

阶段Ⅱ的主要思想是将原模型的MINLP 问题分解为MILP 子问题和NLP 子问题进行交替迭代求解，FP算法的框架［17］如附录A图A1所示。

1）MILP子问题。

MILP子问题的数学模型为：

式中：JF、Jg分别为等式约束、不等式约束的雅可比矩阵。式（15）的约束中：第1个、第2个公式由外逼近法［18］在当前点生成；第3 个公式为整数割，用于避免FP 算法多次求解到同一整数解而陷入死循环。

式（15）为存在绝对值的非凸优化问题，因此本文引入辅助变量ηi将式（15）中的目标函数转化为式（16）所示形式。

经过上述转化后MILP问题成为凸优化问题，且与式（15）等价，因此可利用线性规划求解器对其进行求解。

2）NLP子问题。

松弛后的NLP子问题数学模型为：

经过转化后的NLP子问题可利用NLP求解器直接进行求解。

模型中NLP 子问题的解存在2 种情况：①若NLP子问题的目标函数为0，则当前连续变量以及二进制变量的解为MILP子问题的可行解；②若NLP子问题的目标函数不为0，则说明在当前条件下，通过求解NLP 子问题无法找到满足电压稳定裕度约束的可行解。松弛后的二进制变量表示若将节点i处的发电机加入MILP 问题的发电机中，则可以使NLP 子问题的解收敛至1 个可行解，需要再次将该解传递给MILP 子问题并进行下一步的计算。由于NLP 子问题为非凸优化问题，该问题的解可能收敛至1 个局部最优解，此外，由于在阶段Ⅰ移除了无效发电机，搜索空间维度由2ng降低为2ng-m，同时整数割约束可以防止FP 算法陷入死循环。虽然FP算法可以快速寻找到最优解，但是解的质量依赖于初始点的选取，而MILP 子问题可为FP 算法提供接近最优解的初始点。

2.3 模型求解

最少发电机调整数量问题的求解步骤如下。

1）输入当前系统的发电计划、网络参数、负荷预测数据、运行人员期望负荷裕度提升的比例α以及候选发电机与对应的可调整范围，计算基态系统的负荷裕度λbase。

2）根据式（13）对发电机有功出力进行灵敏度计算，将候选发电机分别归入集合U和D并进行排序，将筛选后的集合U和D中的发电机状态作为下一阶段模型求解中离散变量的初始值。置迭代次数k=1，最大迭代次数设为kmax。

3）求解式（15）所示的MILP 子问题，得到第k次迭代的解，并将其传递至NLP 子问题模型中。

4）求解式（17）所示的NLP 子问题，得到第k次迭代的最优解

6）输出优化后系统的负荷裕度λpost以及所需调整的发电机与对应的调整量。

求解流程图如附录A图A2所示。

3 算例分析

本文以IEEE 118 节点系统和IEEE 300 节点系统为例进行仿真验证。测试平台为MATLAB 2018b，采用Yalmip 工具包对模型进行求解，分别调用求解器Gurobi 和IPOPT 对MILP 子问题和NLP 子问题进行求解。

3.1 IEEE 118节点系统发电机优化调度结果分析

该算例系统中共包含54 台发电机，系统总负荷为4 242 MW 和1 438 Mvar。节点33 — 69、76 — 81、97 — 99、116、118 处的39 个负荷在基础水平上增长20 %，其余负荷保持不变，负荷模型采用恒功率模型。设置节点1、4、31处的3台发电机有功注入增长分别为75.705、54.705、86.52 MW，用于平衡负荷增长需求。此时基态系统的负荷裕度为2 218.2 MW，即λbase=10.255 2。

假设运行人员期望负荷裕度提升的比例α=10 %，应用阶段式求解方法对模型进行求解，阶段Ⅰ的候选发电机筛选结果如表1 所示（表中列出了候选集合U中排序前10 台的发电机和候选集合D中排序后5 台的发电机；G40表示节点40 处的发电机，其余类似）。

表1 阶段Ⅰ的候选发电机筛选结果Table 1 Screening results of candidate generators in Stage Ⅰ

将筛选和排序后的发电机送入下一阶段进行详细计算，阶段Ⅱ的0-1 变量和有功出力调整量迭代结果如表2所示。

表2 阶段Ⅱ的0-1变量和有功出力调整量迭代结果Table 2 Iteration results of 0-1 variables and active power output adjustment in Stage Ⅱ

由表2 可知：在第1 次迭代过程中，通过求解MILP 与NLP 子问题得出发电机G40、G42和G26是需要进行调整的发电机；在第2 次迭代过程中，将第1次迭代结束后2 个子问题解中的差异项（发电机G42和G26的有功出力）通过NLP 子问题对MILP 子问题的结果进行修正，此时2 个子问题的目标函数相同，迭代停止。通过采用本文所提求解方法将发电机G40、G42的有功出力分别上调100、73.41 MW 以及将发电机G26的有功出力下调173.41 MW 后，优化后系统的负荷裕度λpost=11.280 7，满足静态电压稳定性提升需求。

为验证所提求解方法的准确性，在不同负荷裕度提升需求下对B & B 方法和本文方法进行对比，结果如表3所示。

表3 不同负荷裕度提升需求下B & B方法与本文方法的求解结果对比Table 3 Comparison of solution results between B & B method and proposed method under different load margin promotion demands

由表3 可知：本文方法的求解结果与B & B 方法的求解结果基本一致，验证了本文方法的正确性；在α分别为5 %、10 %、15 % 时，本文方法的求解时间分别为2.978、5.346、9.882 s，显著短于B & B 方法的求解时间；在α为15 % 时，B & B 方法由于离散变量搜索空间较大而陷入局部最优，最终导致迭代次数超过最大迭代次数，无法收敛。

3.2 IEEE 300节点系统发电机优化调度结果分析

该算例系统共包含69 台发电机、411 条线路和68个负荷，节点257为平衡节点，系统总负荷有功功率为23 525.85 MW。节点207 — 231 处的19 个负荷在基础水平上增长15 %，其余负荷保持不变，负荷模型采用ZIP 模型，分别设置ap=aq=0.3、bp=bq=0.3、cp=cq=0.4。设置节点260 — 263处的4台发电机注入功率增长分别为108、108、118.82、210.74 MW，基态系统的负荷裕度为1 042.6 MW，即λbase=1.748 9。若此时运行人员期望负荷裕度提升的比例α=5 %，应用阶段式求解方法对模型进行快速筛选。阶段Ⅰ的快速筛选结果如附录A 表A1所示，离散变量的搜索空间维度由269降低至215，极大地降低了模型的求解难度。阶段Ⅱ中发电机的状态及1 个可行解如附录A 表A2 所示，经过2 次迭代后MILP 和NLP 这2 个子问题的目标函数相同，输出最终需要调整的发电机及对应调整量，调整后系统的负荷裕度λpost=1.836 3，满足静态电压稳定提升要求。

在相同的负荷裕度提升需求下B & B 方法与本文方法的求解结果对比如表4 所示。由表可知：本文方法比B & B 方法的耗时约减少90 %；B & B方法的发电机调整数量与本文方法的发电机调整数量相等，但发电机有功出力的调整量比本文方法的大，这是由于B & B 方法所得结果中的发电机G98在本文方法的阶段Ⅰ中因灵敏度过低而被移除，从而使得在相同的负荷裕度提升需求下灵敏度较小的发电机调整量更大。仿真结果进一步验证了本文方法的有效性。

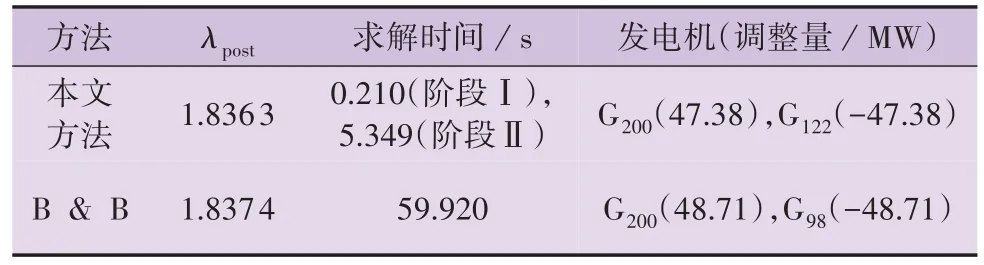
表4 相同的负荷裕度提升需求下B & B方法与本文方法的求解结果对比Table 4 Comparison of solution results between B & B method and proposed method under same load margin promotion demand

4 结论

为了解决电压稳定控制中控制设备数量过多的问题，本文提出了一种以最少发电机调整数量为目标的电压稳定紧急控制数学模型，同时提出了含快速筛选和模型转化的阶段式求解方法，极大地加快了模型的求解速度。算例测试结果验证了本文所提方法的有效性。此外，与B & B 方法计算结果的对比体现了本文所提方法稳定的收敛性和较好的优化效果。

本文研究了通过发电机有功出力调整来提高静态电压稳定性的方法，笔者后续将考虑利用线路切换、变压器分接头调整等多种控制措施的协同组合来进行预防控制的情况。

附录见本刊网络版（http：//www.epae.cn）。