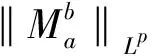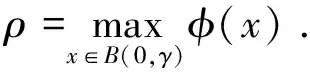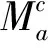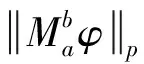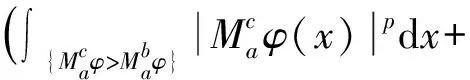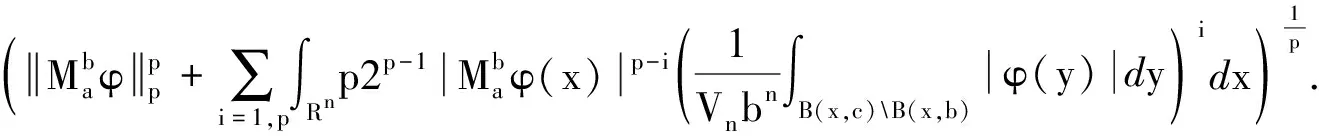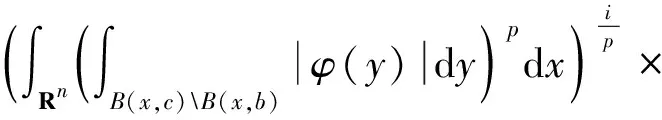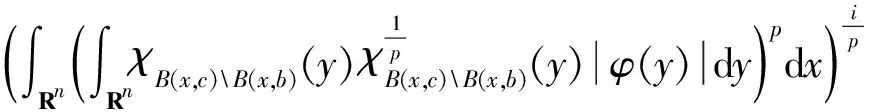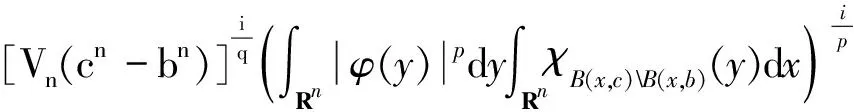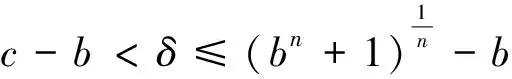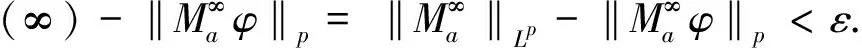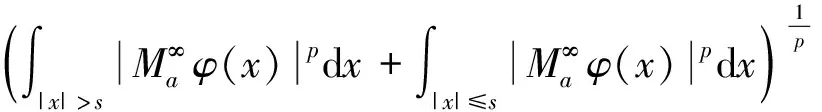Continuity of the Lp-norm of the truncatedHardy-Littlewood maximal operator*
2024-01-19WUJiaWEIMingquanYANDunyan
WU Jia, WEI Mingquan, YAN Dunyan†
(1 School of Mathematical Sciences, University of Chinese Academy of Sciences,Beijing 100049, China 2 School of Mathematics and statistics, Xinyang Normal University, Xinyang 464000, Henan, China) (Received 27 September 2021; Revised 2 November 2021)
Abstract This paper focuses on the continuity of Lp(Rn)→Lp(Rn)-norm of the truncated Hardy-Littlewood maximal operator is extended to infinity.
Keywords truncated maximal operator; continuity; Lp(Rn)→Lp(Rn)-norm
The purpose of this paper is to establish the continuity ofLp(Rn)→Lp(Rn)-norm of the truncated Hardy-Littlewood maximal operator.
1 Introduction
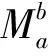
(1)
whereB(x,r) denotes the ball centered atx∈Rnwith the radiusr. Note that by the absolute continuity of the Lebesgue integral, forb<∞, we have
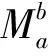
Recall that for a locally integrable functionf, the classical Hardy-Littlewood maximal operatorMis defined by
The classical Hardy-Littlewood maximal operator is a fundamental tool to study harmonic analysis, potential theory, and the theory of partial differential equations[1-2].
Meanwhile, how to compute the continuity of the operator norm of the classical Hardy-Littlewood maximal operator is an important problem.
As is known to all, the truncated operators have many significant properties and are closely related to their corresponding operators. For example, as shown in Ref.[3], theLp-boundedness of the truncated operator is equivalent to that of its corresponding oscillatory operator. Therefore, in order to facilitate and simplify our study of the classical maximal operators, we can first study truncated maximal operators and try to figure out their relationships with the classical maximal operator.
As long as 0 holds for anyx∈Rn. It then follows that (2) (3) Furthermore, applying inequality (2) to the functiongin formula (3), one can show thatgis precisely an increasing function. Moreover, in the casep=1, Wu et al.[6]give the explicit expression ofg(and extend their result to the case of general strong truncated Hardy-Littlewood maximal operator), and hence show the continuity ofgin this setting. Motivated by these works, in this paper, we place our emphasis on exploring the continuity ofgfor the casep>1. Now we formulate our main theorems as follows. Theorem1.1Letp>1be a real number. Then the functiongin formula (3) is a continuous function forθ∈[1,∞]. Remark1.1It is noteworthy that the continuity of casep=1 discussed in Ref.[6] can be viewed as a complement to our theorem to yield that for anyp≥1,gis a continuous function. The rest of the present paper will be organized as follows: In section 2, we will give some lemmas. Before we proceed to prove our main results, several basic lemmas are needed. The first lemma is used to reduce the space we consider, while the second one is a technical lemma which is useful in the proof of Theorem 1.1. Lemma2.1For 0 The proof of Lemma 2.1 is just a repetition of the proof of Lemma 2.5 in Ref. [4], and hence we omit it. Lemma2.2Supposeα,βare two positive real numbers. For 1≤p<∞, we have (α+β)p≤αp+p2p-1αp-1β+p2p-1βp. Proof: Applying the Taylor formula yields that (α+β)p≤αp+p(α+β)p-1β. then the desired result follows from the fact that (α+β)p-1≤2p-1(αp-1+βp-1), and some simple calculations. Now, we are in the position to give the proof of the continuity ofgwith respect toθ. ProofofTheorem1.1 For clarity, we will give the proof in three steps. (i)gis left semi-continuous. (ii)gis right semi-continuous. (iii)gis continuous at the infinity. Step 1.We first prove thatgis left semicontinuous at the pointbsuch thata For any ε>0, we apply lemma 2.1 to yield that there exists someφ∈Cc(Rn) with‖φ‖p=1, such that Then we further take Consequently, we can obtain that (4) which yields (5) Sinceb-c<δ, there holdsb/c<1+δ/c. Observe thatδ (6) Substitute inequality (6) into formula (4), we can deduce that where the second inequality holds due to Lemma 2.2, and we use the fact thatδ≤εp/sin the penultimate inequality. To sum up, Therefore, for anyε>0, there exists aδ=min{1,εp/s,b-a} wheresis defined as above, such that for all 0 ɡ(c)≤g(b)≤g(c)+2ε. As a result,gis left semicontinuous at the pointb>a. Step 2. Furthermore, we proceed to prove that the functiongis right semicontinuous at the pointbsuch thata≤b<∞.Let us start by giving some notations that will be used in the proof of this part. First, we set C=‖M‖Lp, that is,Cis theLp-norm of the classical Hardy-Littlewood maximal operator. Then we define Now, for anyε>0, take Using Lemma 2.1, we can reduce our discussion to functionsφinCc(Rn) with ‖φ‖p=1.Supposec (7) which yields (8) Using Lemma 2.2, it then follows from formula (7) and formula (8) that (9) Now we give the estimate of the quantities (10) in formula (9), wherei=1,p. Applying Holder’s inequality to quantity (10), we can calculate that (11) where the penultimate inequality and the last equality hold because of our choices ofCandφ. However, our current estimate formula (11) is not sufficient to deduce our desired result. Therefore, to get a much more delicate estimate of formula (10), we should give a precise evaluation of quantities in formula (11). Letqbe the conjugate exponent ofp,which is,1/p+1/q=1. By once again using Holder’s inequality, we have =[Vn(cn-bn)]i (12) Combining the estimates of formula (11) and inequality (12) together, it follows that (13) By the arbitrariness ofφ, we can reach the conclusion thatg(c)≤g(b)+ε. ≤ɡ(b)+ε. ɡ(b)≤ɡ(c)≤ɡ(b)+ε. Consequently,gis right semicontinuous at the pointb≥a. Step 3. At last, we provegis continuous at the infinity. Following from Lemma 2.1 again, for anyε>0,there exists someφ∈Cc(Rn) with ‖φ‖p=1, such that Suppose thatφis supported in the ballB(0,γ)withγ>0. (14) Moreover, one can compute that ≤εp, (15) whereωn-1is the surface area of the unit ball inRn, and the last inequality holds because of our priori choice ofs. Substitute formula (15) into formula (14), we can further obtain that LetN=s+γ. Then for anyc>Nand anyx∈{|x|≤s}, we have As a result, for anyc>N, it follows that (16) In terms of formula (16), we can deduce that g(∞) =2ε+g(c). To sum up, for all ε>0, there existsN=s+γwheresand γ are defined as above, such that for anyc>N, there holds ɡ(c)≤ɡ(∞)≤ɡ(c)+2ε. Consequently,gis continuous at the infinity. Now, as far as step 1, step 2, and step 3 are completed, our proof is then finished. We sincerely appreciate Shao Liu for his insightful suggestions on the proof of our main theorem.
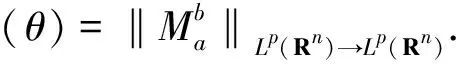
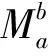
2 Some facts and lemmas
3 Continuity of the Lp-norm of the truncated maximal operator