双曲空气弹簧的理论研究及有限元分析
2024-01-19廖文激
廖文激
(广州大学土木工程学院,广州 511370)
引言
隔离振动技术是大型高端超精密仪器测量及制造的一项基础设施技术,也是衡量一个国家先进设施测试及制造能力的标志性技术之一。随着科学技术的不断发展,大型高端超精密仪器的加工精度和测量水平的逐渐提高,在其加工,安装,测量及运行过程中会受到隔离环境中因地面脉冲导致的微观振动干扰。地面脉冲振动低频为主,以地脉动的形式传播,衰减速度逐渐变慢。微观振动会影响精密仪器的功能,降低工作精度,加大构件的疲劳变形[1],从而缩短精密仪器的使用寿命。因此,环境微观振动对大型高端超精密仪器有着越来越高的要求[2],该要求在超精密加工,超精密测量,光谱技术领域等领域尤为突出。
常见的隔振结构有磁负效应弹簧、碟形弹簧[3]、欧拉压杆结构[4]及空气弹簧等。磁负效应弹簧隔振器具有可调的刚度,且其可调精度非常高,是一种新型的非线性隔振器。但由于该隔振器需要磁场才能工作,因此不适合一些对磁场敏感的场所使用。蝶形弹簧是小型精密设备常用的一个隔振元件,但由于它的工作原理与欧拉弹簧类似,因此,其也面临着与欧拉弹簧一样的耐久性的困境。空气弹簧具有自振频率低、竖向静刚度可调、承载能力通过气压控制承载力等优点,适合用于对洁净和磁场强度有要求的科学实验室。因此,本文结合空气弹簧的结构特点以及工作原理,对空气弹簧的理论进行研究,并运用有限元软件对理论公式进行验证,以证明其合理性。
1 空气弹簧的组成部分
空气弹簧主要由上盖,气囊,下座构成。气囊与上盖,下载接口的连接方式有螺栓固定式,密闭式以及自封式。空气弹簧主要有囊式空气弹簧和膜式空气弹簧这两种结构[5]。囊式空气弹簧可以分为单曲式,双曲式以及多曲式空气弹簧。因为曲囊数量过多会降低空气弹簧的横向稳定性,所以一般不超过四曲。为了减少曲囊间的摩擦,双曲式以上空气弹簧需要安装金属胶环。膜式空气弹簧的连接方式可以分为自由模式和约束模式。不管压缩还是伸张,膜式空气弹簧的有效面积变化比较小,而囊式空气弹簧有效面积变化比较大。膜式空气弹簧的刚度小,有比较低的自振频率,但其耐用度不足,寿命短[6]。然而,囊式空气弹簧刚度比较大,其固有频率比较高,耐用度则相对好得多,但制造工艺复杂,成本高[7]。

图1 囊式及膜式空气弹簧
2 空气弹簧的理论分析
在任何温度和任何压强下都能严格地遵从气体实验规律(查理定律、盖-吕萨克定律及玻意耳马略特定律),这样的气体叫做“理想气体”。 理想气体状态方程是描述理想气体在处于平衡态时,各状态参量间关系的状态方程。理想气体状态方程可以用压力p、温度T 和体积v表示,数学表达式如下:
式中:
n—气体物质的量;
R—比例系数,不同状况下数值有所不同,单位是J/ (mol K)。
对时间求导可得:
由热力学第一定律:
式中:
△U—气体内能增量;
Q—气体状态变化吸收的热量;
W—气体为外界所做的功。
气体内增量也可以表示为:
式中:
CV—定容比热。
假设在空气弹簧工作过程中,气体与外界没有发生热量交换,即气体状态变化吸收的热量为零。整理可得:
由于该过程为绝热过程,所以:
式中:
CP—定压比热容;
k—绝热指数,当气体为空气时取值为1.4。
根据压强公式,有效面积可以表示为:
式中:
F—空气弹簧主气室反力;
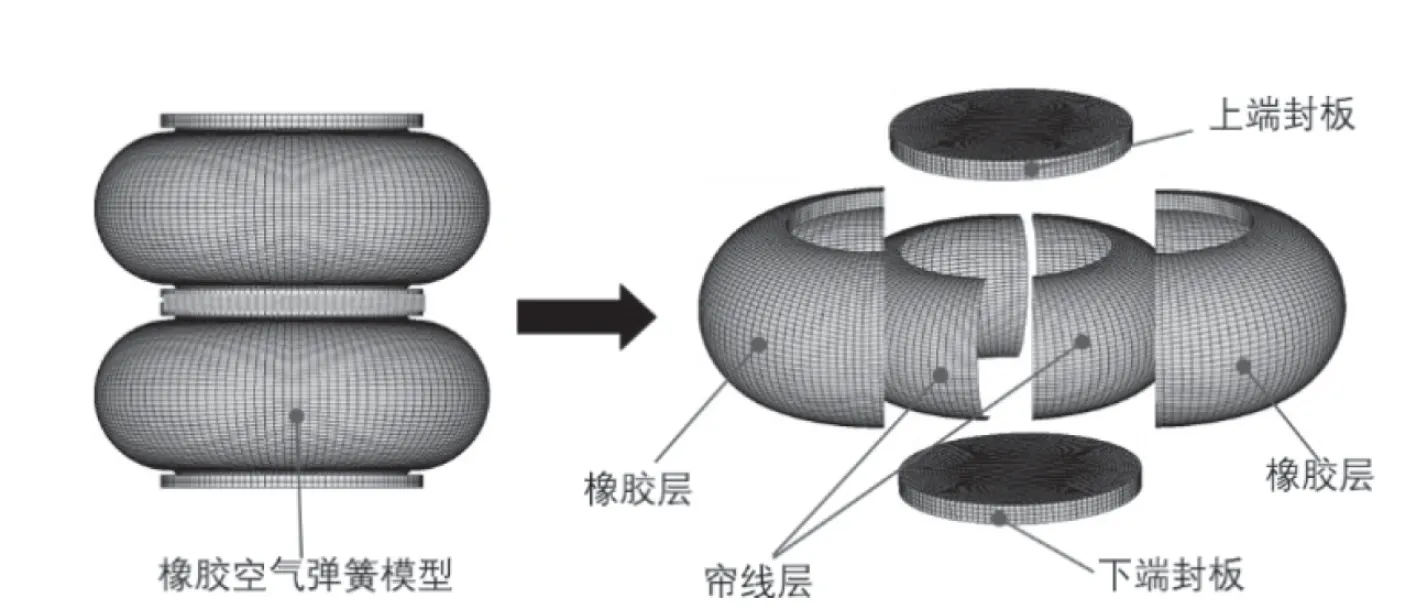
图2 空气弹簧的有限元模型
P—空气弹簧主气室气囊压强;
Pa—标准大气压;
Ae—有效面积;
VA—主气室体积;
z—空气弹簧工作时的竖向位移。
理想气体的定压比热CP与定容比热的差为定值R,当气体物质的量n=1 mol,整理能量方程可得:
当主气室受到压缩后,则主气室体积减少Av·z,同时主气室气体质量减少q。在空气弹簧工作过程中,其竖向变形均在工作高度附近。为了简化计算,假设气体密度不变,其中,ρo 为主气室初始气体密度,P0为主气室初始气压:
3 空气弹簧的有限元分析
3.1 单元选择
应用ABAQUS 有限元软件对双曲式空气弹簧进行模拟分析,有限元模型的构成可以分为上、下端封板,橡胶层,帘线层三部分。其中上、下端板选择六面体单元,橡胶层选择六面体单元,帘线层选择S4R 壳单元。
3.2 材料单元模型
空气弹簧上、下端封板的变形很小,可以视为刚体,所以选择ABAQUS 软件中的Mooney-Rivlin 模型模拟橡胶层[8]。帘线层是空气弹簧的主要承载部件,要求拥有良好的耐用性和耐压性[9],ABAQUS 软件提供加强筋结构的Rebar单元能合理的模拟帘线层复合材料的特性[10]。假设在空气弹簧工作过程中,气体的温度和质量不会发生变化,则气体是理想气体,遵循理想气体状态方程,与理论推导保持一致。在上端封板边界上施加均布载荷表示气体压力,在下端封板施加全约束以固定主气室。使用ABAQUS中充腔气体单元来模拟主气室内的气体[11]。气体通过下端封板进气口进入主气空以模拟空气过程,如图3 所示。
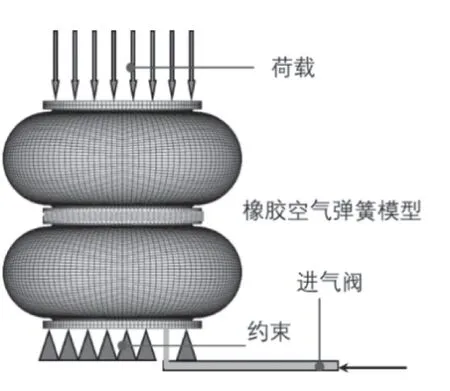
图3 边界条件
3.3 模拟分析
对双曲式空气弹簧充气过程进行有限元模拟,比较双曲式空气弹簧充气高度与直径的试验数据与模拟数据。从表1 中可以看出,两者非常接近,两者之间的误差比较小,验证空气弹簧有限元建模方法合理性。在此基础上,为了研究初始气压对空气弹簧静刚度的影响,在(0.3~0.6)MPa 不同初始气压下对空气弹簧进行试验,并对静刚度进行仿真,从而得到相应的变化曲线。

表1 空气弹簧试验数据以及模拟数据
从图4 可以看出,双曲式空气弹簧的静刚度曲线在整体趋势上与试验曲线保持一致。随着双曲式空气弹簧的初始气压增大,其承载能力大幅度提高,表明初始气压对空气弹簧静刚度影响比较大。在实际应用中,可以适当增大双曲式空气弹簧初始气压来提高其承载能力,从而满足不同工况下承载能力要求。
4 结论
对双曲式空气弹簧进行了建模与分析,可得出以下结论:
1)结合空气弹簧的结构特点,对空气弹簧进行了理论计算的公式推导,得出了空气弹簧的压强关系式。
2)建立双曲式空气弹簧有限元模型,并根据实际工作进行模拟,验证了所建模型的准确性。
3)增加空气弹簧的初始气压,能提高空气弹簧的承载能力,对空气弹簧的研究及运用提供了一定的借鉴作用。
