二维三次映射的混沌动力学
2024-01-18陈凤娟丁文豪
陈凤娟, 丁文豪, 钟 溢
(1.浙江师范大学 数学科学学院,浙江 金华 321004;2.宁波工程学院 理学院,浙江 宁波 315211)
0 引 言
1979年,Holmes[1]研究了如下Duffing方程:
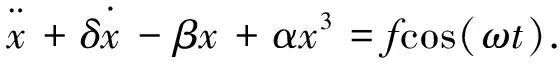
(1)
式(1)中,δ,β,α,f,ω是参数.对固定的δ,β,α,ω>0,当f∈(1.08,2.45)时,方程(1)存在奇异吸引子.为了考察该吸引子的结构,Holmes研究了方程(1)的Poincaré映射,并提出了如下差分方程:

(2)
式(2)中,a,b∈R是参数.当a=2.77,b=0.20时,映射(2)存在如图1(a)所示的吸引子;当a=2.67,b=0.20时,映射(2)存在似Hénon吸引子[2],如图1(b)所示;当a=2.30,b=1.00时,映射出现“8”字形吸引子,如图1(c)所示.上述数值结果的初值均取(x0,y0)=(0.1,0.1),这些吸引子具有正Lebesgue测度的吸引域.而Smale马蹄的吸引域往往是Lebesgue零测集[3], 因此,难以在数值模拟中观测到.那么,映射(2)是否存在Smale马蹄呢?
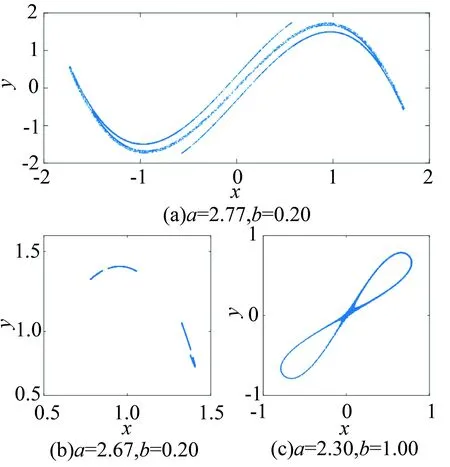
图1 映射(2)的吸引子
1 主要结果

定理1当0<|b|<1,20a3≥50a2+8a2|b|+135R2(1+|b|)2时,映射F在区域D中存在不变集Λ.进一步,系统(F,Λ)拓扑共轭于三符号动力系统(σ,Σ(3)),其中σ是双边移位映射.
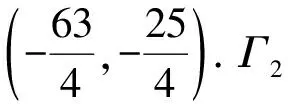
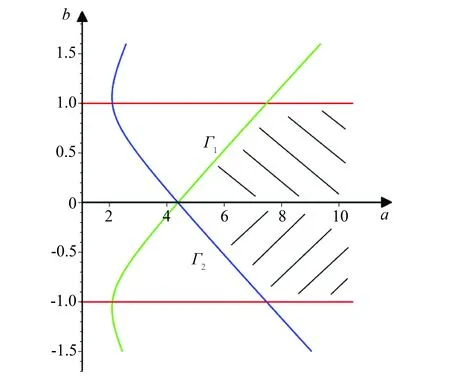
(a)0<|b|<1,20a3≥50a2+8a2|b|+135R2(1+|b|)2
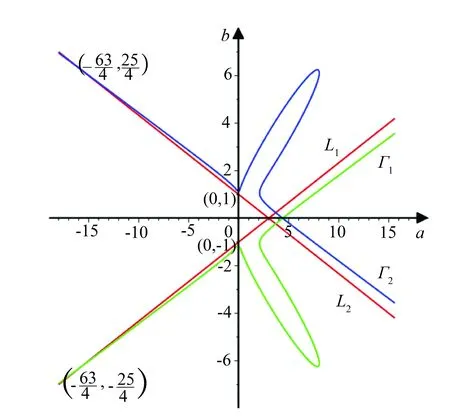
(b)三次曲线Γ1,Γ2和直线L1,L2
下面通过两步完成定理1的证明.首先,在定理1的条件下作出Smale马蹄的横条和竖条,得到映射F的不变集Λ.然后,运用Moser定理[4],证明(F,Λ)拓扑共轭于三符号动力系统.
2 定理1的证明
在证明定理1之前,首先介绍Moser定理和n次复系数多项式的零点性质.
假设U1,U2,…,UN是D中N个互不相交的横条,V1,V2,…,VN是D中N个互不相交的竖条.横条Ui和竖条Vi的直径分别记作d(Ui)和d(Vi)(i=1,2,…,N).
条件(Ⅰ):对于i=1,2,…,N,F(Ui)=Vi.而且F把Ui的横边映射成Vi的横边,Ui的竖边映射成Vi的竖边.
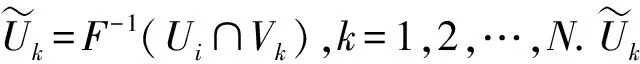
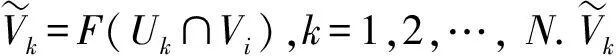

条件(Ⅲ+):dF(Sp)⊂SF(p),并且满足|η0|≤μ|η1|.
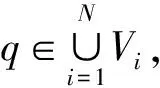
条件(Ⅲ-):dF-1(Tq)⊂TF-1(q),并且满足|ξ1|≤μ|ξ0|.
注1满足条件(Ⅰ)与条件(Ⅲ+)、条件(Ⅲ-)意味着条件(Ⅱ)成立.

文献[5]运用Moser定理,对著名的Hénon映射给出了存在Smale马蹄的参数条件.进一步,文献[6]推广了Moser定理.
下面的引理描述了多项式零点的导数性质.

根据定理1,有如下推论:
推论1在定理1的条件下,对任意的x,c∈[-R,R],实系数三次多项式P3(y)=ay-y3-|b|x+c存在3个互不相同的实零点.
证明对三次方程P3(y)=0,应用卡丹公式得到
对任意x,c∈[-R,R],
根据定理1的条件可知
Δ<0.
应用卡丹定理,P3(y)存在3个互不相同的实零点.推论1证毕.


(3)
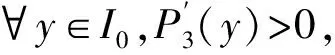

(4)

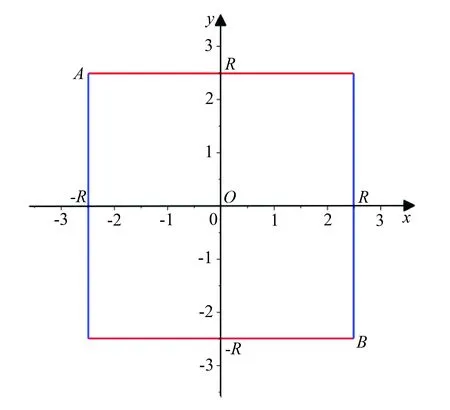
(a)a=5.0,b=0.2时的区域D
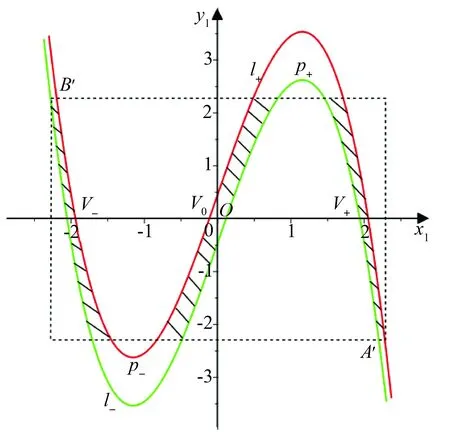
(b)3个竖条V+,V0和V-
下面确定竖条的原像.记F-1是F的逆映射.根据式(2),得
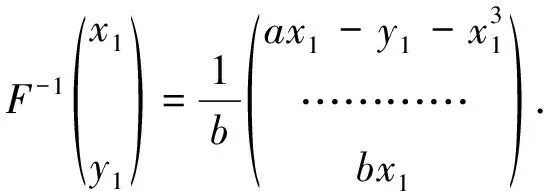
(5)
根据前面的分析,V+,V0和V-的竖边是三次曲线l+,l-上的一部分,因此,它们的原像是D的竖边x=∓R的一部分.V+,V0和V-的横边位于直线段y1=±R上.根据式(5),y1=R和y1=-R的原像分别是三次曲线s-:bx=ay-y3-R和s+:bx=ay-y3+R,如图4所示.s+与s-亦互相平行,且s+位于s-的右边.经过类似计算知道,三次曲线s+与s-的极值点均位于区域D的外面.因此,F-1(D)∩D是D中的3个横条形区域,记作H+,H0和H-.它们由三次曲线s+,s-与直线段x=±R所围.


图4 F-1(D)与D相交所得的3个横条H+,H0和H-
以上分析了0 下面运用Moser定理证明(F,Λ)是混沌动力系统.先考虑0 (6) 任取(ξ0,η0)∈S(x,y),那么 (7) a-3y2>a-3(y*)2>0. 根据定理1的条件知 |a-3y2|>a-3(y*)2. 根据式(5),逆切映射是 (8) (9) (10) 由定理1条件以及0 因此,对任意(x1,y1)∈V0, dF-1(T(x1,y1))⊂TF-1(x1,y1), 以上证明了0 总之,根据Moser定理[4],映射(2)在区域D上存在不变集Λ,而且系统(F,Λ)拓扑共轭于双边符号动力系统(σ,Σ(3)).这表明二维三次映射F在D上存在Smale马蹄意义下的混沌动力学.定理1证毕. 一般地,对Rn上的微分同胚F,周期点的Lyapunov指数有以下结论: 引理2[8]假设p是F的m周期点,Jacobi矩阵J=D(Fm)在p点的特征值和特征向量分别是λj和vj(j=1,2,…,n),那么,在p点vj方向的Lyapunov指数由下式计算: 引理3[8]假设p点的Jacobi行列式det(DF(p))=Δ是常数,那么,当p点的Lyapunov指数均存在时, l1(p)+l2(p)+…+ln(p)=ln(|Δ|). 下面计算映射(2)的不动点和2周期点的最大Lyapunov指数. O+和O-的特征值相等,它们是: 通过计算,映射(2)存在3条2周期轨道,分别是: 3){(-ζ2,-χ2),(-χ2,-ζ2)}. 取a=5.0,b=0.2时,3条2周期轨道的Lyapunov指数谱分别是(精确到小数点后6位): 1)l1=2.608 986…,l2=-4.218 424…; 2)l1=1.811 355…,l2=-3.420 793…; 3)l1=1.811 355…,l2=-3.420 793…. 因此,不动点和2周期点的最大Lyapunov指数均大于0. 本文研究了由式(2)定义的映射的混沌动力学,通过Moser定理证明了该映射在不变集上拓扑共轭于三符号动力系统.如下2个问题有待于进一步研究: 1)映射(2)是否存在闪回排斥子? 2)映射(2)是否存在横截同宿轨道?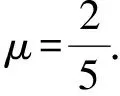

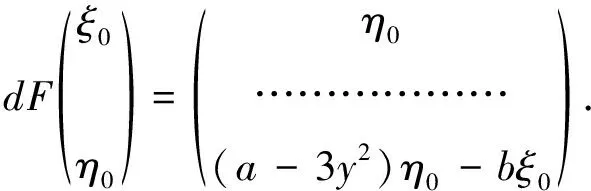
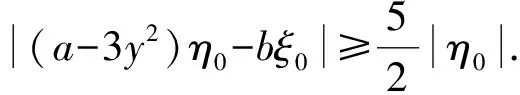

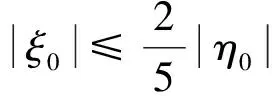
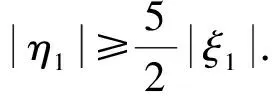
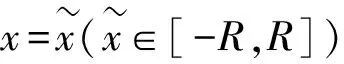

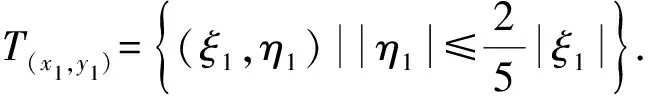
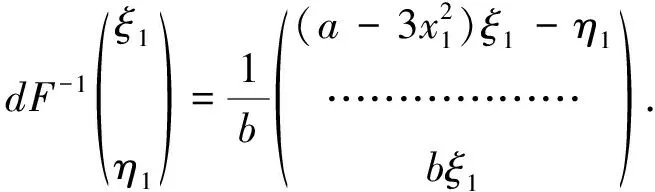
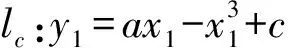
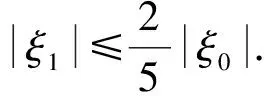
3 周期点的最大Lyapunov指数

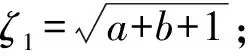
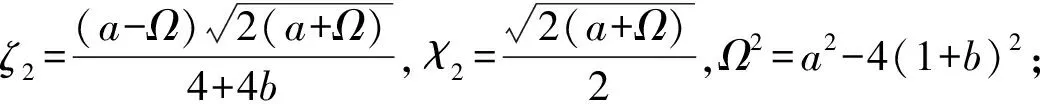
4 结 语
