基于IBES-XGBoost的高速铁路沿线风速预测模型*
2024-01-18孟建军江相君孟高阳李德仓
孟建军,江相君,孟高阳,李德仓
(1.兰州交通大学 机电技术研究所,甘肃 兰州 730070;2.甘肃省物流及运输装备信息化工程技术研究中心,甘肃 兰州 730070;3.甘肃省物流与运输装备行业技术中心,甘肃 兰州 730070;4.兰州交通大学 机电工程学院,甘肃 兰州 730070)
当前我国高速铁路总里程数已突破4万km,高速铁路遍布全国各地。而在影响列车运行的诸多自然灾害中,风灾的作用较为显著[1]。我国幅员辽阔,大部分地区处在季风区,冬春季节受蒙古-西伯利亚高压影响盛行冬季风,夏秋季节主要受东南季风影响,特定的季节主导风向容易形成较强势力,进而形成大风天气。我国许多高速铁路段都处在大风的威胁中。例如,兰新铁路第二双线新疆段近60%线路需要穿越大风区[2]。东部沿海地区遭受台风灾害的影响非常严重[3]。由大风引起的行车事故在世界各国屡见不鲜,在我国的南疆线等强风区,曾多次出现列车脱轨、倾覆事故[4]。因此,建立一套行之有效的风速预测方法对高速铁路沿线的大风预测预警尤为重要。
风速预测相关算法层出不穷,随着人工智能相关理论日趋成熟,许多相关算法逐渐应用到风速预测领域。XU等[5]将长短期记忆神经网络(Long short-term memory neural network,LSTM)和卷积神经网络相结合的方式进行风速预测。TUERXUN等[6]先对风速数据进行分解,而后使用LSTM辅以改进的金枪鱼群优化算法进行风速预测。LI等[7]先使用变分模态分解对风速数据进行分解,并采用粒子群算法(Particle Swarm Optimization,PSO)优化双向长短期记忆神经网络(Bidirectional Long Short Term Memory,Bi-LSTM),进而完成风速预测。SHEN等[8]使用卷积神经网络(Convolutional Neural Network,CNN)和LSTM相结合的方式进行风速预测。BOMMIDI等[9]使用完全集合经验模态分解(Complete Ensemble Empirical Mode Decomposition With Adaptive Noise,CEEMDAN)分解风速数据,再使用Informer进行风速预测。向玲等[10]使用变分模态分解(Variational Mode Decomposition,VMD)对风速数据进行一次分解,再使用CEEMDAN对风速数据进行二次分解,最后使用LSTM进行风速预测。以上方法均为改进深度学习模型,或将深度学习模型与分解算法、智能优化算法等方法相结合。这些方法能在一定程度上解决风速预测问题,但还存在一系列问题。例如,神经网络算法存在可解释性差、计算时间长等问题[11],部分算法未结合其他气象要素进行预测等。此外,王瑞[12]指出,高速铁路大风预警信息应至少提前3 min预测,因此对逐分钟风速数据进行提前三步进行风速预测是高速铁路大风预警业务的最重要的组成部分。
针对以上存在的问题,本文使用XGBoost融合改进的秃鹰搜索算法(Improved Bald Eagle Search Algorithm,IBES)构建提前三步风速预测模型。最后,利用逐分钟风速数据集进行验证,使用多个评价指标对比IBES-XGBoost与其他模型的精度。结果表明,所提模型相比其他众多模型具有较高预测精度。
1 理论基础
1.1 XGBoost算法
XGBoost对梯度提升回归数进行了改进[13],相比于传统的Boosting实现方法,XGBoost在训练速度和预测精度上都有了提升。XGBoost对损失函数进行了二阶泰勒展开,同时引入两个正则化项求解整体最优,并使用线性搜索方法寻找弱学习器。树的集成模型为:
(1)
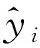
XGBoost的目标函数为:
(2)
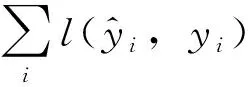
式(2)中Ω(fk)的表达式为:
(3)
式中:γ和λ为权重系数,T为叶子节点的数量,ω为各叶子节点的分数。
在t次迭代时,目标函数为:
(4)
对式(4)进行二阶泰勒展开可得式(5):
(5)

1.2 秃鹰搜索算法
秃鹰搜索算法(Bald Eagle Search Algorithm,BES)是ALSATTAR等[14]提出的群智能优化算法。该算法模仿秃鹰的捕猎行为,在给定空间内进行寻优。该算法分为三个阶段,第一阶段为秃鹰选择最佳搜索空间,第二阶段为秃鹰在选定的空间内进行搜索,第三阶段为秃鹰从最佳位置俯冲向猎物。
在选择搜索空间阶段,秃鹰根据猎物数量选择最佳搜索区域(选择猎物量大的区域),具体数学描述如式(6)。
Pnew,i=Pbest+α×r(Pmean-Pi)。
(6)
式中:Pbest为秃鹰根据先前搜索情况确定的最佳位置,α是区间[1.5,2]内取值的控制位置变化的参数,r为区间(0,1)内产生的随机数,Pmean为先前搜索结束后秃鹰的平均分布位置,Pi为第i个秃鹰的位置。
在选定空间内搜索阶段,秃鹰在选定的空间以螺旋状飞行,寻找最佳俯冲位置,具体数学表达式如式(7)~(11)所示。
Pi,new=Pi+y(i)×(Pi-Pi+1)+x(i)×(Pi-Pmean);
(7)
(8)
xr(i)=r(i)×sin(θ(i)),yr(i)=r(i)×cos(θ(i));
(9)
θ(i)=α×π×rand;
(10)
r(i)=θ(i)+R×rand。
(11)
式中:a∈(5,10)为搜索点和中心点之间的夹角,R∈(0.5,2)用于确定搜索周期数,θ(i)和r(i)分别为螺旋方差的极角与极径,x(i)和y(i)取值在(-1,1)内用于表示极坐标下秃鹰的位置,rand为[0,1]内的随机数。
在俯冲向猎物阶段,秃鹰从搜索空间内最佳位置俯冲向目标猎物,种群内其他个体也向最佳点移动,具体数学表达式如式(12)~(18)所示。
Pi,new=rand×Pbest+x1(i)×(Pi-c1×Pmean)+y1(i)×(Pi-c2×Pbest);
(12)
(13)
(14)
xr(i)=r(i)×sinh(θ(i));
(15)
yr(i)=r(i)×cosh(θ(i));
(16)
θ(i)=a×π×rand;
(17)
r(i)=θ(i)。
(18)
式中:c1,c2∈[1,2],且均用于增加秃鹰俯冲时向最佳点和中心点移动的强度。
2 改进秃鹰搜索算法
BES虽然收敛速度和精度优于大部分智能优化算法,但是仍然存在陷入局部最优和部分问题求解精度不高等问题。本文从增强全局搜索能力和增强局部搜索能力两个角度出发,提出了一种改进的秃鹰搜索算法(IBES)。首先,在种群初始化阶段使用Tent混沌映射替代BES的初始化策略,以此增强种群的多样性,提高全局搜索能力。其次,每间隔一定的迭代次数,若算法收敛情况较差,则在BES的基础上进一步采用BFGS拟牛顿法进行搜索,从而增强局部的搜索能力。
2.1 Tent混沌映射
BES的初代种群,是在搜索空间中通过随机数生成的。通过随机数产生的种群,其多样性可能较差,进而导致寻优结果较差。而混沌映射具有随机性和遍历性的特点,这些特性可以保持种群的多样性,使智能优化算法摆脱局部陷阱,提算法的全局探索能力。目前常用的混沌模型较多,FAN等[15]指出,大量实验表明,Tent混沌映射在目前常用的混沌映射中性能最好。Tent映射能在[0,1]内产生分布较为均匀的数值,应用于智能优化算法后能够产生分布较为均匀的初始种群。
Tent混沌映射的表达式为:
(19)
当u=0.5时,Tent混沌映射的均匀性最好[16]。因此,本文所用的Tent混沌映射公式为:
(20)
2.2 BFGS拟牛顿法
拟牛顿法是牛顿法的一种改进。BFGS拟牛顿法求解Hessian矩阵的近似矩阵,避免每次迭代都要计算Hessian矩阵,从而大大降低了计算的复杂度。BFGS拟牛顿法是一种经典的局部搜索策略[17],部分学者研究表明在智能优化算法中加入BFGS拟牛顿法可以加快收敛速度[18-19]。
若目标函数在定义域上二次连续可微,则对函数f(x)在xk+1处作二阶泰勒展开可得:
(21)
对式(21)进行求导可得:
g(x)≈gk+1+Gk+1(x-xk+1)。
(22)
式中:gk+1为梯度值,Gk+1为Hessian矩阵。
令yk=gk+1-gk,x=xk,sk=xk+1-xk,则有:
yk≈Gk+1sk。
(23)
使用近似Hessian矩阵Bk+1替代Gk+1即可得到拟牛顿条件,拟牛顿条件为:
yk=Bk+1sk。
(24)
式中:近似Hessian矩阵Bk+1向Hessian矩阵做近似逼近的迭代公式为:
(25)
在算法迭代过程中,使用Armijo准则确定每次迭代的步长[20]。若已知当前位置xk和近似Hessian矩阵确定的搜索方向dk,指定β∈(0,1)且σ∈(0,0.5),步长因子αk=βmk,mk为满足式(26)的最小非负整数。
(26)
故可得下一个位置,下一位置为:
xk+1=xk+αkdk。
(27)
3 模型建立
3.1 基于IBES-XGBoost的提前多步风速预测模型
根据上文所述理论基础和业务背景,构建基于IBES-XGBoost的提前多步风速预测模型。由于XGBoost的超参数对预测结果影响较大,故采用改进的秃鹰搜索算法参数对XGBoost的学习率、树的最大深度和回归树数量进行寻优。
建立预测模型流程图(图1),具体步骤如下:

图1 基于IBES-XGBoost的风速提前多步预测模型
1)输入原始数据,根据皮尔逊系数筛选和风速数据正相关的特征。
2)划分数据集,将前90%的数据集作为训练集,后10%的数据作为测试集。
3)对数据集进行归一化处理,并构建XGBoost模型。
4)使用IBES对XGBoost的学习率、树的最大深度和回归树数量进行寻优。使用Tent混沌映射生成初始种群,使用XGBoost模型作为目标函数,采用BES原搜索策略的同时加入BFGS拟牛顿法加强局部搜索能力,找到最优的初始参数组合。
5)用步骤4)的寻优所得的初始参数进行训练,训练得到XGBoost模型后即可进行测试。
6)将数据反归一化,并计算评价指标。
3.2 模型评估指标
将测试集预测结果进行量化评价,用平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方根误差(RMSE)作为精度的评估指标。拟合优度(R2)作为拟合程度的评价指标。具体公式为:
(28)
(29)
(30)
(31)
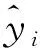
4 实验分析与验证
4.1 IBES性能测试
为了验证所提改进秃鹰搜索算法的有效性,选用三个基准测试函数进行测试(表1)。表1中F1~F2为单峰测试函数,F3为多峰测试函数。单峰测试函数可以测试寻优精度,多峰测试函数可以测试全局寻优能力和收敛速度。

表1 基准测试函数
选择IBES、BES、GWO和PSO四种算法在4个测试函数上进行测试,种群初始数量均设置为30,迭代次数均为500,各个算法均独立运行30次。考虑到迭代次数较多,在进行性能测试时IBES间隔50次迭代判断一次是否使用BFGS拟牛顿法进行寻优。测试结果见表2,表中加粗字体为最佳值。由表2可知,IBES在多个基准测试函数上的性能明显优于其他三个算法,其精度大幅度优于其他算法。并且IBES的标准差也远小于其他算法,这说明IBES的寻优结果都集中在较小的区间内,算法的稳定性更优。各函数三维模型及算法收敛曲线见图2~图4。
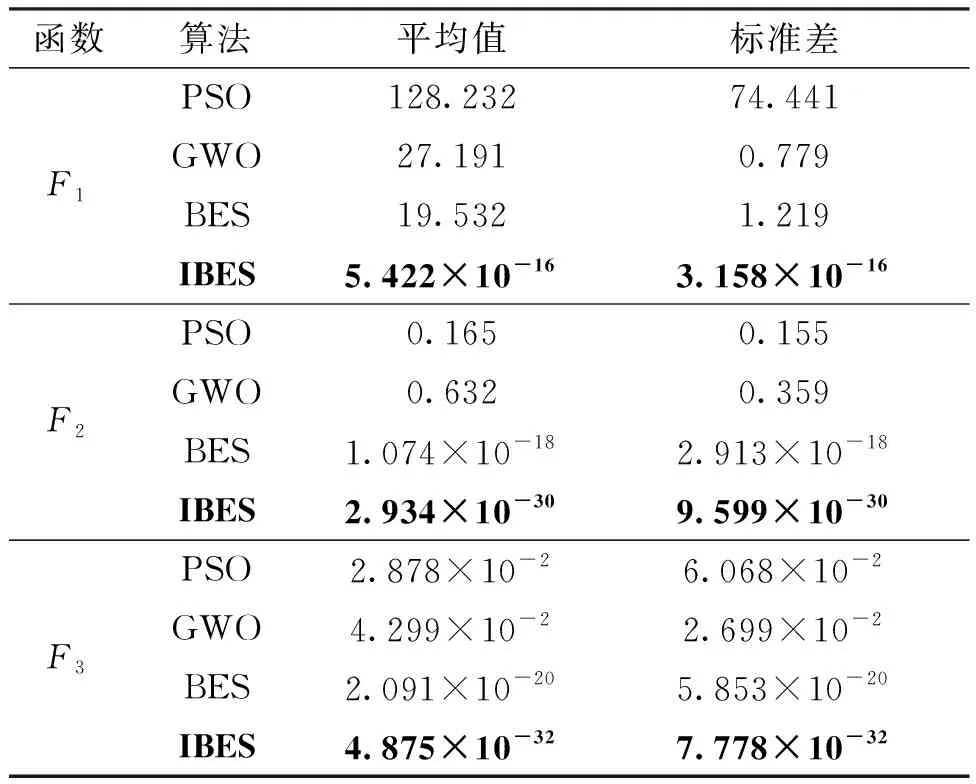
表2 智能优化算法在基准函数上测试结果

图2 函数F1三维模型及收敛曲线
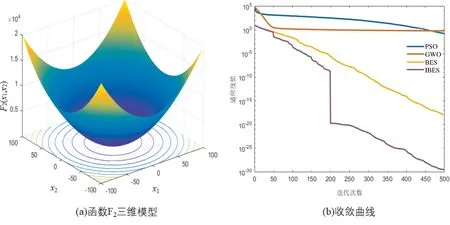
图3 函数F2三维模型及收敛曲线
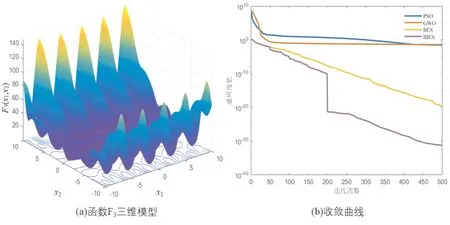
图4 函数F3三维模型及收敛曲线
由图中可以看出,IBES可以快速接近全局最优解,而其他算法则会陷入局部最优。随着迭代次数的增加,IBES借助BFGS拟牛顿法能进一步靠近最优值。
4.2 数据分析与预处理
风速容易受到其他气象因素变化的影响[21],因此考虑使用皮尔逊相关系数对比风速和温度、风寒温度、露点温度等其他气象因素的相关性,从而选取相关性强的气象要素作为模型的特征输入。风寒温度指数衡量在一定气温和风速的情况下人体感受到寒冷的程度,低(高)风寒温度代表低(高)温和强(弱)风[22]。皮尔逊相关系数计算公式为:
(32)
数据集选用美国可再生能源实验某观测点的逐分钟观测数据[23],共计选取22 257条数据。选取前90%数据作为训练集,后10%数据作为测试集。该数据集除风速数据外还包含逐分钟的部分气象信息。
由各气象要素与风速之间的皮尔逊相关系数(表3)可知,在该数据集风速与温度相关性较强,风速与风寒温度和露点温度相关性较弱。因此选用温度作为特征输入模型。

表3 气象因素与风速之间的皮尔逊相关系数
为提高模型的准确性和稳定性,同时避免极端值对模型产生影响,故对输入数据进行归一化,对输出预测值进行反归一化得到最终风速数据。归一化公式为:
(33)
式中:xi为第i个原始数据,xmin为该数据的最小值,xmax为该数据的最大值,xnorm为归一化后的数据。
4.3 预测结果
为验证IBES寻优预测模型时的优越性,将IBES与PSO、GWO及BES进行对比,对数据集进行逐分钟数据的提前3步预测。XGBoost的学习率、树的最大深度和回归树数量寻优范围分别为[0.01,03]、[2,100]和[5,1 000]。为确保实验的公平性,各智能优化算法的初始种群数目均设为20,最大迭代次数均设为15。从(图5)可以看出,IBES具有较快的收敛速度,Tent混沌映射策略能够生成更具有代表性的初始种群,BFGS拟牛顿法能够加速收敛速度,并提升迭代后期的寻优能力,二者令IBES获得最优的适应度值。4种算法寻优所得的最佳XGBoost超参数见表4。

表4 智能优化算法对XGBoost超参数寻优结果
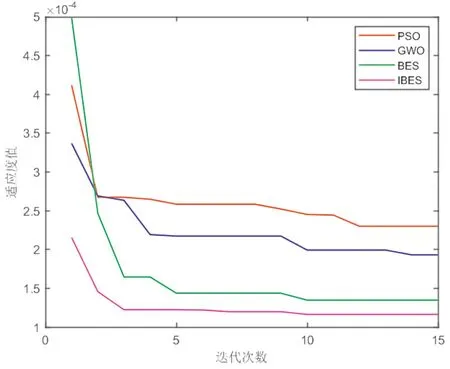
图5 各算法对XGBoost预测模型寻优时的适应度曲线
为全面评估模型性能,将IBES-XGBoost、BES-XGBoost、GWO-XGBoost、PSO-XGBoost、XGBoost和LSTM六种模型在测试集上的提前三步预测结果进行对比分析。单一XGBoost的学习率设置为0.3,树的最大深度设置为6,回归树的数量设置为100。LSTM的最大迭代次数为500,隐藏层神经元个数为200,学习率为0.000 1。各模型的提前三步预测结果(图6)可以看出,IBES-XGBoost的拟合程度最好,其在波动较大的区间内也展现出了较好的预测效果。BES-XGBoost、GWO-XGBoost、PSO-XGBoost和XGBoost在波动较大的采样点附近,预测精度不如IBES-XGBoost。LSTM在波动较大的区间内预测效果较差,拟合程度远不如其他模型。
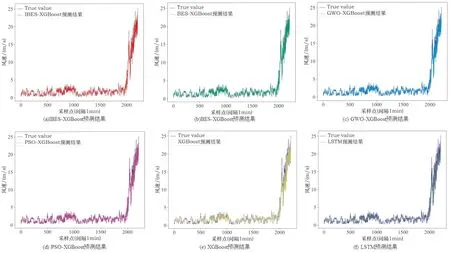
图6 各模型提前3步预测结果对比
从(表5)各模型预测结果的评价指标可以看出,IBES-XGBoost的各项评价指标均为最优。相比于XGBoost,IBES-XGBoost的RMSE、MAE和MAPE分别降低了0.271 m/s、0.085 m/s和2.215%,拟合优度提升了0.012。相比于LSTM,IBES-XGBoost的RMSE、MAE和MAPE分别降低了0.746 m/s、0.419 m/s和21.439%,拟合优度提升了0.055。相比于BES-XGBoost、GWO-XGBoost和PSO-XGBoost,IBES-XGBoost在各项评价指标上均有不同幅度的提升。
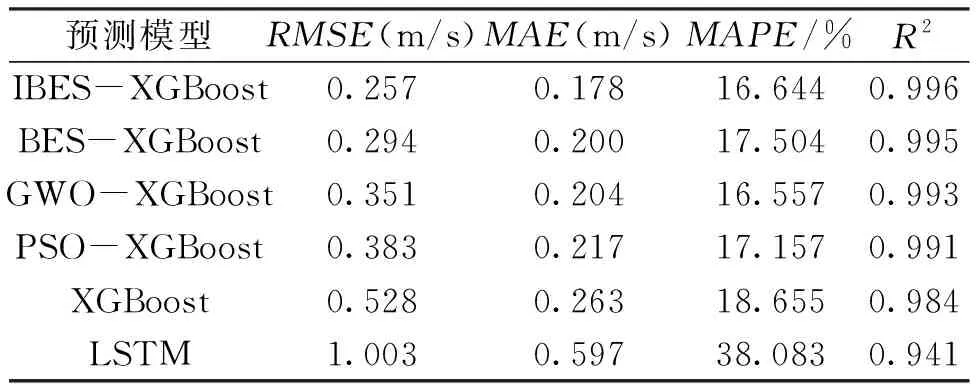
表5 各模型预测结果的评价指标
虽然IBES-XGBoost各项评价指标均为最优,但是我国高速铁路采用分级限速模式,对于不同的风速采取不同的限速措施。因此还需对预测结果分区间进行统计分析,判断预测结果与实际值是否处于同一区间。
根据(表6)我国高速列车在不同风速下的限速标准[24]。标准,对各模型预测结果进行统计,判断预测值和真实值是否处于同一风速区间。由统计结果表7可知,IBES-XGBoost的预测值与真实值处于同一风速区间的准确率最高,其准确率高达99.728%,优于其余预测模型。主要原因在于,IBES-XGBoost预测精度较高,对诸多接近风速区间边界值的数据进行预测时能有较高的效果。因此,IBES-XGBoost根据高速铁路业务需求的逐分钟风速提前三步预测的预测结果,在高速铁路风速限速标准下能得到最高的准确率。

表6 高速列车在不同风速下的限速标准

表7 各模型预测值与真实值处于同一风速区间的准确率
5 结论与讨论
本文从高速铁路风速预测的需求入手,采用IBES-XGBoost对逐分钟风速数据进行提前三步预测。采用Tent混沌映射和BFGS拟牛顿法改进秃鹰搜索算法,能够有效提升秃鹰搜索算法的性能,进而提升对XGBoost超参数的优化能力。在本文的对比实验中,IBES-XGBoost的各项评价指标均优于所对比模型,具有更高的预测精度和拟合能力,验证了所提模型的有效性。根据高速列车在不同风速下的限速标准对各模型预测结果分析可得,IBES-XGBoost具有极高的准确率,因此该方法能为高速铁路沿线风速预测提供参考。
