吉林省森工林区形高表编制

王鹤智,刘奇峰,朱万才*

(1.国家林业和草原局林草调查规划院,北京 100714;2.黑龙江省林业科学研究所,哈尔滨 150080)

林分形高是衡量林分蓄积量的重要指标,即单位面积林分蓄积量和相应的胸高总断面积的比值[1]。在测算林分蓄积量时,只需要测定林分的胸高总断面积,并乘以相应的形高值,就可以得到林分的蓄积量。因此,林分形高在森林资源的调查、监测,特别是森林资源规划设计调查中具有重要作用。为了获取林分形高的数值,通常使用林分形高模型。这种模型是通过林分平均高与林分形高之间的相关关系来建立的,根据调查得到的林分树高可以推算得到相应的林分形高。许多研究者已经对林分形高进行了广泛的研究。刘小平等[2]人在对海南省的桉树、木麻黄等树种建立的模型中,预估精度高达98%以上。余松柏等[3]人拟合了广东省的杉木、马尾松等树种的林分形高模型,证明了林分形高表在测算精度上优于一元材积表; 不同林分起源和树种组成需要采用不同的数学模型来推算林分形高。例如,自然对数函数可以精确解释杉木地上生物量和蓄积量[4],而二次多项式模型适用于杉木、马尾松、华山松、柏木和栎类等树种,幂函数模型[5]适用于阔叶林。使用总体平均模型来估算林分的蓄积量可能会产生较大的误差。因此,可以利用样地的平均胸径和平均树高数据,调整和修订树高与胸径之间的回归模型,以减小估算误差。这样可以提高林分形高的估算精度。总而言之,林分形高是测算林分蓄积量的重要指标,其通过林分平均高与林分形高之间的相关关系模型来获取。不同的起源和树种组成需要采用适合的数学模型。修订回归模型可以减小估算误差并提高估算精度[6],这些研究对于森林资源调查、监测和规划设计具有重要意义。

始林的森林资源,为主要林区的主要树种编制了林分断面积蓄积量标准表,然而,随着时间的推移,我国的森林资源结构发生了显著的变化,现在主要以天然次生林、天然残次林和人工林为主,占全国乔木林面积的79.62%,而未经人为干扰的天然林分仅占4.76%[7]。例如,黑龙江重点国有林区的天然原始林仅2.4万hm2[8],占东北重点国有林区乔木林面积的0.28%,占全国乔木林面积的0.01%。因此,沿用传统林分断面积蓄积量标准表会导致估测精度偏低的问题[3]。为了满足当前森林资源调查工作的要求,快速、有效地计算蓄积量,我们有必要结合现实林分状况重新编制形高表。

研究利用吉林省重点国有林区不同林分类型地面实测样地数据,探索林分形高建模与评价方法,旨在建立适用于不同林分类型的形高模型,为森林资源调查提供更科学、更精确的依据。这样的研究将对我国的森林资源规划和管理产生积极的影响。

1 研究地区概况

研究区域位于吉林省重点国有林区(包含吉林森工与长白山森工)经营区,典型针叶树种有红松(Pinuskoraiensis)、落叶松(Larixgmelinii)、樟子松(Pinussylvestrisvar.Mongolica),阔叶树种有胡桃楸(Juglansmandshurica)、水曲柳(Fraxinusmandshurica)、黄菠罗(phellodendronamurense)、杨树(PopulusLina)、白桦(Betulaplatyphylla)、椴树(Tiliatuan)。

本研究的数据来源主要由3部分组成:2018年在主要林分类型中设置临时样地的调查数据。这些临时样地的设置与调查方法都是按照《森林资源规划设计调查技术规程》(LY/T 26424)的规定执行的、2016年相关林业局开展森林资源规划设计调查布设的总体控制样地调查数据、近两次国家森林资源连续调查固定样地的数据。总计有27884个编表样本数据用于本研究的分析。

2 研究方法

2.1 划分林分类型

根据样地中林分的起源、优势树种和树种组成,对林分进行了类型划分。对于面积过小且样本数量较少,不满足编表要求的类型,将其归并到生长发育规律相近的林分类型中。通过这样的划分和归并,共得出了18种林分类型。具体划分情况见表1

表1 林分类型表

2.2 数据处理

对于模型拟合的数据,可能会存在一些异常样本,它们的存在会影响模型的拟合精度,因此,在进行数据建模之前,必须进行异常样本的剔除处理,以提高建模的准确性和可靠性。异常样本的剔除通常分为两个步骤[9]。首先,针对每个林分类型,使用计算机绘制林分平均树高与形高的散点图,通过肉眼判断明显远离其他样点的数据并删除。这类样本通常是由于记录或计算错误等引起的异常值。然后,使用建模样本拟合某一林分形高表的数学模型,并绘制模型预估值与标准化残差之间的残差图。根据拉依达准则,将超出±3倍标准差以外的样本视为异常样本并予以剔除[10]。

在分析过程中发现异常样本共有854个,占样本总数的3.05%。在剔除这些异常样本(包括采伐、造林地、疏林地和样地数据异常等)后,实际用于编制的样本数据共计27133个。将27133块样地按照之前划分的18个林分类型进行整理,得到了各林分类型主要调查因子的统计量统计表,详细信息请参见表2。

表2 各林分类型主要调查因子统计量统计表

2.3 模型选择

考虑到各树种的林学特性和林分生长过程,我们选择了适用于描述平均树高和林分形高关系的统计数学模型作为林分形高表数学模型。具体的模型形式如下:

fh=th×(a+b/(c+th))

(1)

fh=a×(1-exp(-b×th)

(2)

fh=a+exp(b+c/th)

(3)

fh=(th/a+b×th)^2

(4)

fh=a+b/th

(5)

fh=a×th/(th+b)

(6)

fh=a×(th^b)

(7)

fh=a+b×th

(8)

式中:fh为林分形高;th为林分平均高;a、b、c为估计参数。

2.4 模型评价指标

回归分析的最后一步即对所选模型进行全面验证。很多学者认为仅仅依靠建模样本计算的拟合度或检验指标来评价模型的预测能力是不够准确的,因此建议利用独立的检验样本(即未参与建模的样本)来进行模型适用性检验。有些研究认为将整个样本分成建模样本和检验样本进行建模并不能提供额外的信息来评价回归模型的好坏[11],因此建议使用整个样本进行模型建立[12]。然而,对于评价模型的预测能力,许多研究认为"刀切法"(Jackknifing technique)是最适合的方法[13]。因此,在本研究中采用全部数据进行模型拟合,并使用"刀切法"来评估模型的预测能力[14-16],并使用以下6个指标来评估模型:调整后决定系数(Ra2)、均方根误差(RMSE)、总相对误差(TRE)、平均系统误差(MSE)、平均预测误差(MPE)和平均百分比标准误差(MPSE)

3 结果与分析

3.1 模型拟合

吉林森工林区各林分类型林分形高表数学模型参数估计结果和模型的评价指标值(拟合统计量)见表4-1。通过比较Ra2、RMSE以及参数的有效性,最终确定各林分类型的最优林分形高模型,具体拟合结果见表3(仅列出拟合结果最优的组合)。

图1 各林分类型最优林分形高表数学模型拟合曲线

表3 各林分形高模型拟合及参数估计

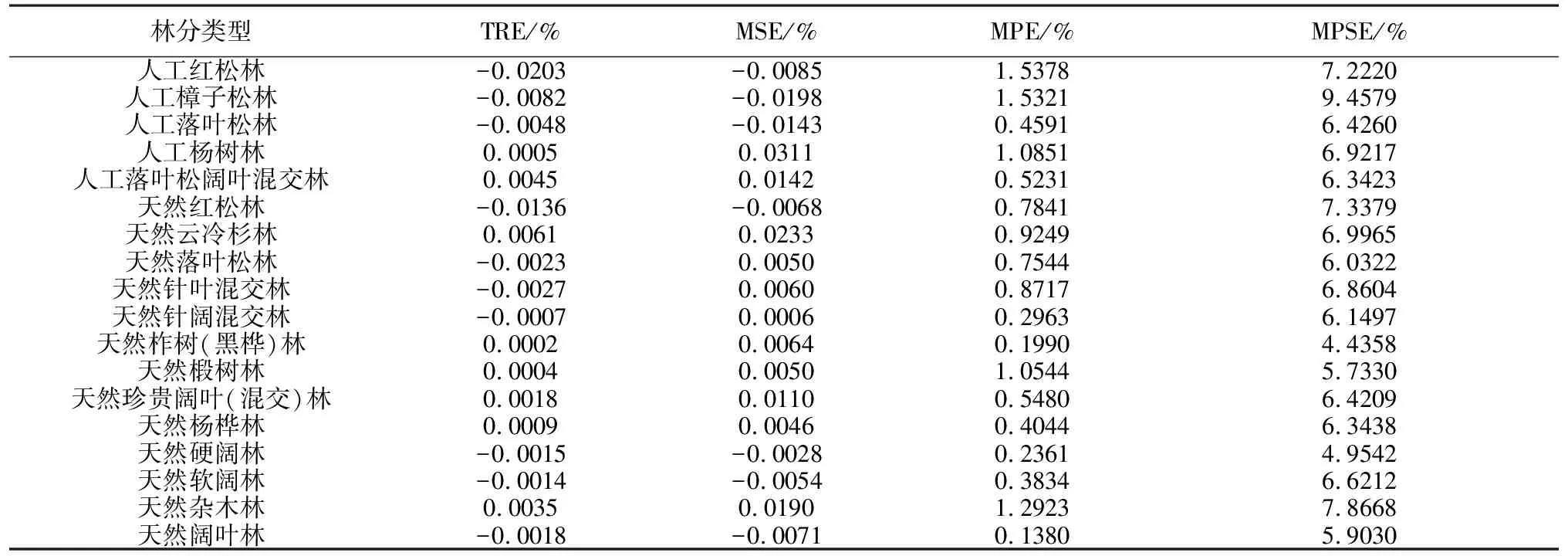
表4 各林分类型最优林分形高模型的检验结果

3.2 模型检验

采用TRE、MSE、MPE和MPSE对最优模型进行评价,评价结果如表6所示。各林分类型的TRE和MSE都在±0.1%以内,这表明模型的总体准确率较高。MPE均小于3%,表明预测结果的个体准确性较高。MPSE均小于12%,表明预测结果与实际观测值之间的差异较小。综上,构建的模型具有较好的预测精度和适用性。

4 讨论与结论

研究基于大量样地实测数据,旨在建立具有代表性的林分形高模型系统,以填补吉林省重点国有林区在这方面的空白。首先,对数据进行预处理,并剔除异常样本。然后,通过比较不同模型的拟合精度,选出了拟合效果最佳的18个不同林分类型的最优林分形高模型。接着,利用“刀切法”评估了这些模型的适用性。该模型系统可以用于编制吉林省重点国有林区林分形高表,表中树高范围可参考表2。在实际应用中,如果林分平均高超过树高最大值,则直接使用模型进行推算。在过去的研究中,由于计算方法和计算工具的限制,为了便于计算,人们常常将样本按径阶分类并以径阶平均值进行模型拟合。此外,为了提高拟合度,还采用了以径阶样本数量为权重进行加权回归,或对因变量进行转换并使用转换后的数值计算拟合度的方法。然而,这些方法都会影响拟合效果的真实性。在本研究中,直接使用全部样本的原始数据进行模型拟合,更符合实际情况。通过“刀切法”验证模型的准确性,证明了采用全部数据拟合模型,并用“刀切法”验证模型的方法是可行的。传统上,形高数学模型的拟合通常使用单一的数学模型。如果指标符合要求,则认为该数学模型适用于该类林分类型。然而,这种方法的局限性是明显的。在研究中尝试了不同的数学模型,包括指数、幂函数和二次多项式等,对不同类型的林分进行拟合。这基本涵盖了所有常见形高模型的种类。在多个数学模型都满足要求的情况下,选择最优模型,从而增加了模型的预测精度和实用性。通常认为回归方程的相关性越高,拟合效果越好。对于数学模型来说,当R2值在0.9以上时,表示模型的因果关系较强。然而,在研究中,由于未考虑立地质量等级对林分形高的影响以及数据的高离散程度,导致R2值偏低。为了更好地反映实际情况,随着研究的进展,我们有必要进一步改进林分形高模型。