柔性套圈对轴承接触特性的影响研究
2024-01-17赵宪龙王燕霜张书玉栗文彬王高峰
赵宪龙 王燕霜* 张书玉 李 晌 栗文彬 王高峰
(1.齐鲁工业大学(山东省科学院),济南 250353;2.山东博特轴承有限公司,聊城 252600;3.八环科技集团股份有限公司,台州 318000;4.烟台天成机械有限公司,烟台 264006;5.洛阳轴研科技有限公司,洛阳 471039)
当轴承外径和轴承内径的比值为1.25 以下时,轴承壁很薄,称为薄壁轴承,如RV 减速器用主轴轴承和风电主轴轴承等。目前,普通轴承接触特性分析均是基于轴承的内、外套圈为刚性套圈的假设,轴承受载后只在滚动体与滚道接触区发生弹性变形。然而,在轴承承受较大径向载荷、套圈外径与内径之比又较小的情况下,轴承内、外套圈的整体弯曲变形的弹性特性凸显,其挠曲变形量已经接近甚至超过赫兹接触变形量。如果依然采用传统的赫兹接触理论计算,结果必与实际值相差较远,因此在计算薄壁轴承载荷分布的过程中应将轴承套圈视为柔性套圈。姚振强等人提出并推导了一种安装在薄壁支座中的向心轴承在受载后各滚动体负荷的力学模型和计算方法[1]。姜祎等人根据谐波传动中薄壁轴承受载工况,提出了薄壁轴承载荷分布计算模型[2-3]。李一耕[4]、张福星[5]和张阳阳[6]等人利用ANSYS 软件,对面-面接触方式中柔-柔接触对推力球轴承接触问题进行求解,指出不考虑套圈变形进行薄壁轴承力学特性计算时误差较大。TEDRIC 在考虑轴承柔性外圈和椭圆内圈情况下,对轴承接触载荷和接触变形进行数值分析[7-8]。但是,对刚性套圈和柔性套圈模型对轴承接触特性具体影响的研究较少。文章以RV 减速器用角接触球轴承和风电主轴圆锥滚子轴承为例,分析柔性套圈和刚性套圈模型对轴承接触特性的影响,为轴承设计提供参考。
1 刚性套圈和柔性套圈模型建立
以RV 减速器用薄壁角接触球轴承和风电机组用圆锥滚子轴承为例,进行刚性套圈和柔性套圈模型下轴承接触特性的对比分析。两种轴承工作时转速较低,因此采用静力学分析方法,忽略保持架、离心力以及陀螺力矩的影响。两轴承内、外圈以及滚动体的材料均为标准轴承钢,具体参数如表1 和表2 所示。
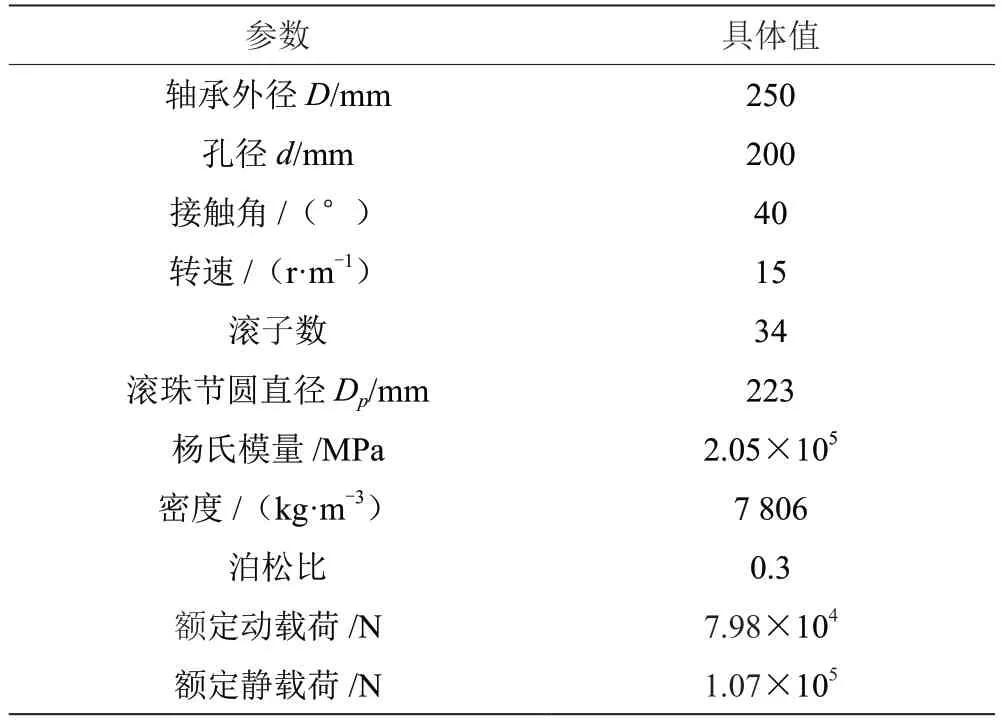
表1 某RV 薄壁角接触主轴轴承特性参数
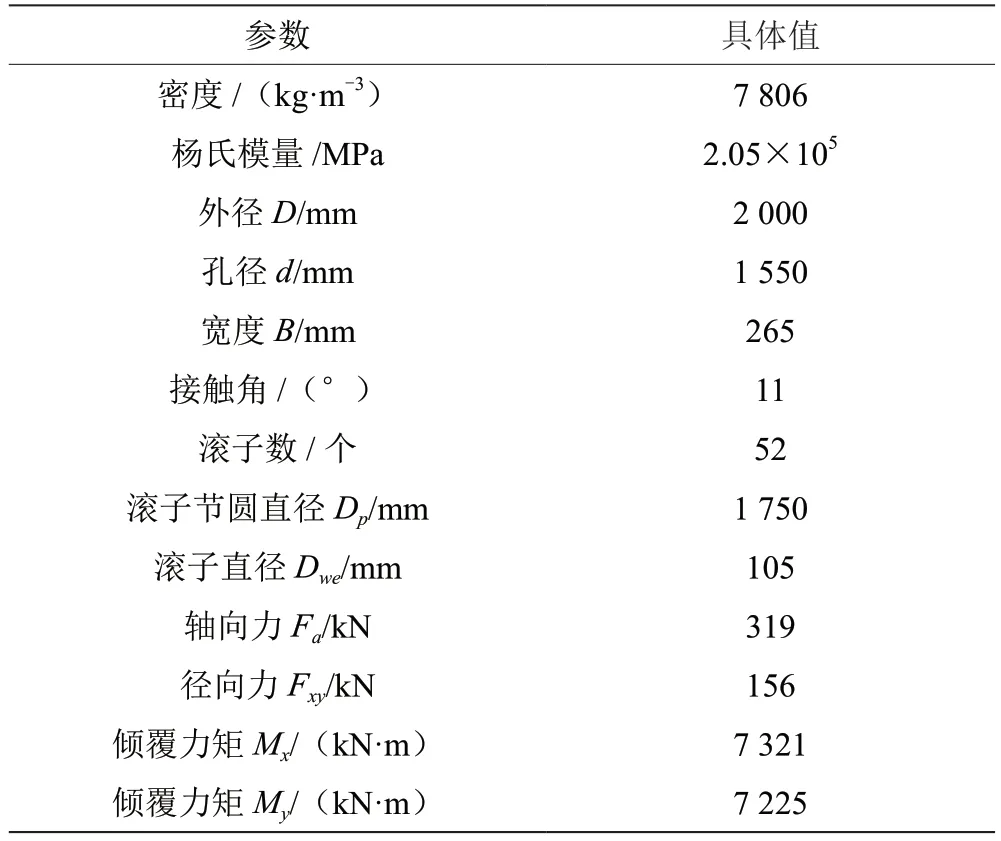
表2 某型号大型风电主轴圆锥滚子轴承参数
基于轴承的各项特性参数,利用Romax 软件建立RV 减速器用薄壁角接触球轴承刚性套圈和柔性套圈等效模型,如图1 和图2 所示。将轴承旋转中心定义为坐标原点,Z轴为轴承轴向方向,两相互垂直的径向方向分别定义为Y轴和X轴,并以X轴正方向为圆周方向的起始位置。
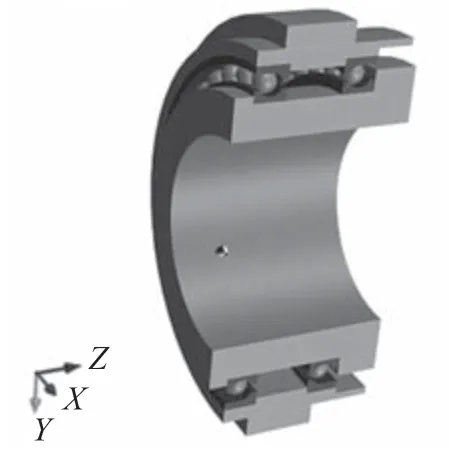
图1 刚性套圈模型

图2 柔性套圈模型
2 接触特性分析
主轴承的各项参数、滚动体数量以及所受的载荷大小,都会对轴承的位移量产生不同程度的影响。不同的位移量尤其是倾覆角度会导致主轴承内圈与外圈的接触状态和接触位置发生改变,进而使主轴承的实际接触角、滚动体载荷分布以及接触变形量发生变化,对滚动体与内、外滚道间的表面接触应力及寿命产生重要影响[9]。
2.1 RV 减速器用薄壁角接触球轴承
RV 减速器用薄壁角接触球轴承在刚性套圈模型和柔性套圈模型假设下,球-滚道接触载荷和最大接触应力如图3 所示。两种模型下,轴承球-内滚道和球-外滚道接触载荷分布几乎重合。通过比较可以发现:柔性套圈模型下的轴承球-滚道接触载荷小于刚性套圈模型下的接触载荷,刚性套圈假设下轴承最大接触载荷为1 955 N,柔性套圈假设下轴承的最大接触载荷为1 791 N,两者最大载荷发生在位置角为90°处。
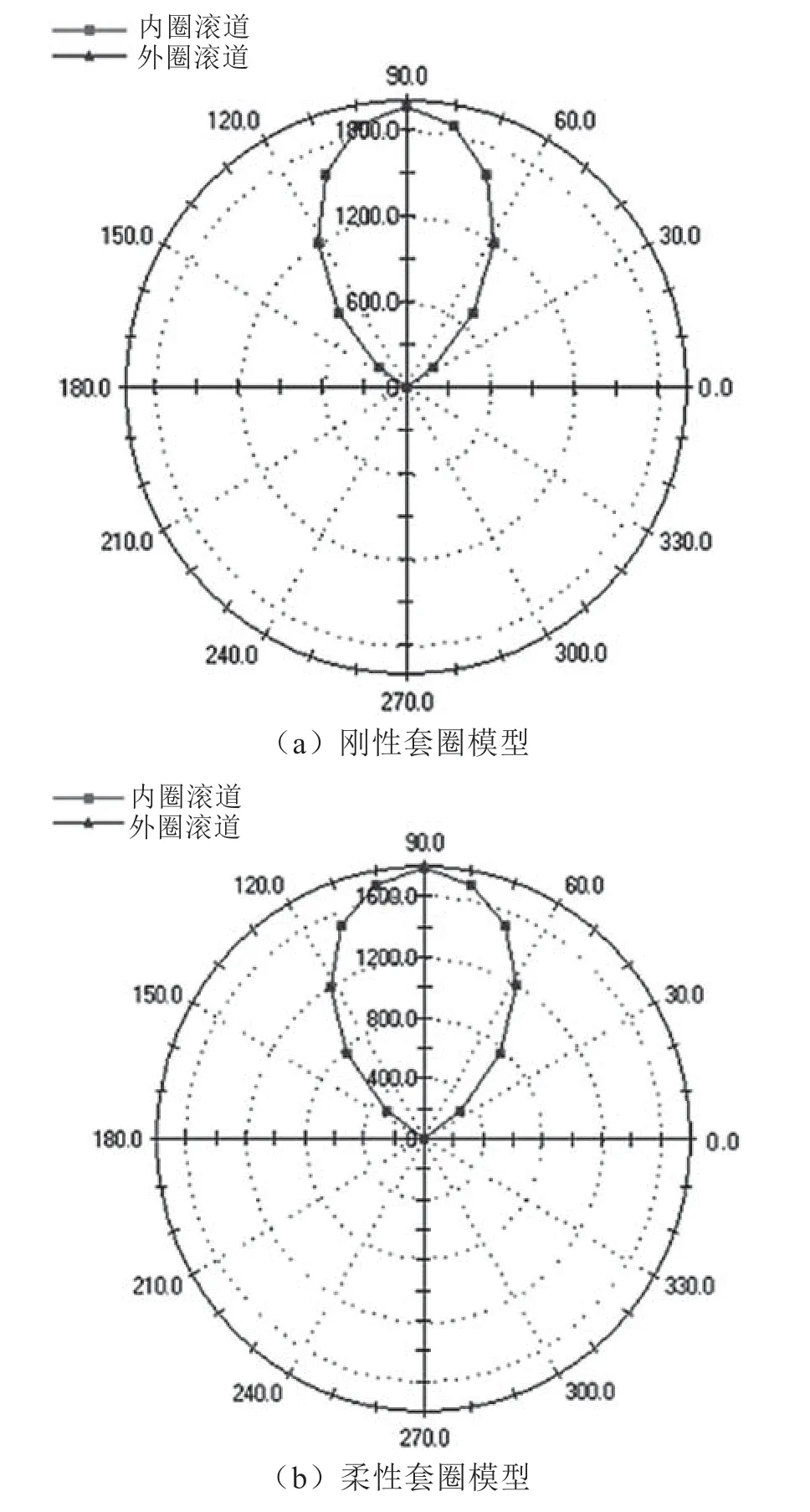
图3 球-滚道接触载荷分布图(单位:N)
两种模型下轴承内外圈滚道最大接触应力的分布,如图4 所示。套圈变形势必导致轴承内部接触特性发生变化。柔性模型下轴承的球-内滚道最大接触应力为1 800 MPa,与刚性模型下的最大接触应力相比低3%;柔性模型下轴承的球-外滚道最大接触应力为1 706 MPa,而刚性模型下相应的最大接触应力为1 758 MPa;二者接触应力分布范围都在30°~150°,且受载滚子数为34 个。

图4 球-滚道最大接触应力分布图(单位:MPa)
两种模型下该薄壁角接触球轴承滚道上的接触斑,如图5 和图6 所示。由于外载荷的作用,钢球与内、外滚道的接触应力和接触椭圆存在显著区别。图5 中每条竖线代表每个滚动体与滚道的接触椭圆,接触椭圆的短轴部分沿滚动体滚动的方向,长轴部分则垂直于滚动体滚动的方向。为简化,将接触椭圆作为直线处理,即忽略椭圆短轴的长度。可以发现:由于轴承中轴向力的影响,钢球的接触斑已从滚道中心线发生偏移。此外,无论是钢球与内滚道的接触斑还是与外滚道的接触斑,柔性套圈模型下的接触椭圆长轴长度大于刚性模型下的接触椭圆长轴长度,进而导致柔性套圈模型下球-滚道接触面积变大,接触应力变小。RV 减速机用薄壁角接触球轴承中,由于轴承套圈壁薄,可看成柔性套圈。柔性套圈变形大,使得载荷分布更加均匀,球-滚道接触面积变大,接触应力变小,导致轴承承载能力增加。

图5 刚性套圈模型下滚动体与滚道接触痕迹

图6 柔性套圈模型下滚动体与滚道接触痕迹
2.2 风电主轴圆锥滚子轴承
刚性套圈与柔性套圈模型下,风电主轴圆锥滚子轴承的最大接触应力雷达图和不同位置角处滚子-内滚道接触应力云图如图7 和图8 所示。从图7 和图8可以看出:按照柔性套圈模型,承载滚子数量多于刚性套圈假设的滚子数量;位置角为60°~210°时,按照柔性套圈模型,最大应力大于刚性套圈假设下的最大应力;其他角度处,刚性套圈模型下最大应力大于柔性套圈模型下的最大应力。究其原因:柔性套圈假设下,较大的套圈错位使得滚子更容易发生倾斜,滚子与套圈的接触位置和接触面积发生变化;位置角为60°~210°时,在倾覆力矩作用下,滚子受挤压减小,滚子与滚道接触面积减小,最大接触应力增加;其他位置角处,滚子受挤压增加,滚子与滚道接触面积增大,最大接触应力减小。可见,风电主轴圆锥滚子轴承中,采用刚性套圈模型设计轴承将会导致最大接触应力被低估,造成轴承承载能力不足。
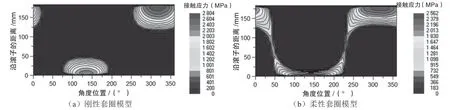
图8 滚子-内滚道接触应力云图
3 结论
分别对RV 减速器用薄壁角接触球轴承和风电主轴圆锥滚子轴承进行刚性套圈模型和柔性套圈模型下的接触特性分析,结合Romax Designer 建立两者的等效模型和接触特性分析,主要结论如下:
(1)RV 减速机用薄壁角接触球轴承中,由于轴承套圈壁薄可看成柔性套圈,而柔性套圈变形更大,使得载荷分布更加均匀,球-滚道接触面积变大,接触应力变小,导致轴承承载能力增加;
(2)对于风电主轴圆锥滚子轴承,在一定的位置角处,柔性套圈模型下最大接触应力大于刚性套圈模型下的最大接触应力,采用刚性套圈模型设计轴承将会导致最大接触应力被低估,造成轴承承载能力不足。
