基于主成分分析的液流电池状态估计策略研究
2024-01-17周剑明吴争光中国联通深圳分公司广东深圳518000
周剑明,戴 鹏,陈 爽,苏 毅,杜 彪,吴争光,杨 翊(中国联通深圳分公司,广东深圳 518000)
1 概述
目前锌溴液流电池(Zinc Bromine Flow Battery,ZBFB)以其高可靠性、长寿命在长时储能领域得到初步应用。锌溴液流电池本身存在电压急剧变化的拐点以及电解液的不规则流动,使得锌溴液流电池荷电状态(State of Charge,SOC)参数模型具有很强的非线性,具体表现为存在大量对SOC 辨识产生影响的扰动参数,特别是放电后期电压拐点导致采样失真,使得开路电压与安时积分等常规方法难以被直接应用[1-4],而SOC 又是影响ZBFB 优化控制的基础参数。因此研究一种可满足ZBFB 放电后期电压拐点处SOC 辨识与校正的方法势在必行[5-6]。
研究表明,数据降维与特征数据提取是提高SOC辨识精度的可行路径之一。而主成分分析(Principal Component analysis,PCA)的主要功能表现在以去除噪声和非特征为表征的数据降维。目前PCA 已在锂电池容量估算、剩余使用寿命预测、多信号特征融合及风电场等值建模等领域得到成功应用。其特点为从特征数据捕捉层面提升数据处理的抗干扰性,从而可有效抑制放电后期电压拐点导致的采样失真与数据丢失对SOC辨识精度的影响。
本文以提高ZBFB 电压拐点处SOC 辨识精度为研究目的,立足于合作企业所设计的ZBFB 样机,在ZBFB 进行100%充放电的条件下,开发一种基于安时积分分析的PCA 优化计算方法,用于提高ZBFB 电压拐点处的SOC 参数的辨识精度。对ZBFB 电压线性变化与非线性变化部分分别采用安时积分与PCA 进行SOC 评估,从算法改进层面有效克服电池放电过程中出现的电压拐点对SOC 计算的影响,提高SOC 计算的精度与效率,从高精度SOC 辨识角度为推进锌溴液流电池在长时储能领域的应用提供参考基础。
2 主成分分析算法基础
主成分分析表现为通过投影进行向量降维,即将N维向量映射为M维向量转换为N维向量在M个基向量投影,如N维向量,M个基向量分别为在基向量的投影为:
通过式(1)完成了降维,降维后的坐标为:
矩阵是由多个列向量组成的,因此矩阵降维思想与向量降维思想一样,只要求得矩阵在各基向量的投影即可。若降维后的样本点尽可能分散,则可用方差表示这种分散程度。
设x(i)表示原始数据,z(i)图片表示投影数据,表示投影数据的平均值,则最大化投影方差可表示为:
基于式(3),得到相应的基向量矩阵W:
其中,tr表示矩阵的迹,即主对角线元素的和;n表示降维后矩阵的维数。基向量矩阵W满足式(5):
PCA 降维是通过样本数据投影到基向量实现的,基向量的个数等于降维的个数,基向量是通过式(5)求解的。
在计算协方差矩阵XXT的特征向量前,需要对样本数据进行中心化,中心化的算法如下:
中心化数据各特征的平均值为0,计算如下:
中心化的过程如下:
每个样本包含n个特征,即:
展开XXT:
只考虑2个特征的协方差矩阵:
一旦得到了协方差矩阵的特征值和特征向量,就可以保留最大的N个特征。PCA的思想是将n维特征映射到k维上(k<n),这k维是全新的正交特征,是重新构造出来的k维特征,而不是简单地从n维特征中去除其余(n-k)维特征。
锌溴液流电池放电后期的电压拐点大概率会导致采样失真或数据丢失,使得安时积分等常规方法进行SOC 计算时会产生较大的误差,从而影响ZBFB 的优化控制。PCA 的优势在于冗杂数据的降维与特征提取,可以通过特征重构确保电压拐点处的电压与电流采样精度,因此可满足ZBFB 电压拐点处SOC 辨识与校正的工程需求,也是本文研究的重点与出发点。
3 ZBFB采样数据分析
在长时储能应用场景下,液流电池的串并组合控制、均流与均压控制均依赖于精确的SOC 计算。受ZBFB 运行时的自放电特性及电解液流速的影响,影响锌溴液流电池SOC 估计的因素较多,表现为电解液的流场和温度场(见图1)、电堆的电磁场等多场耦合微观作用与电池输出电压、电流宏观作用的综合影响。以实验室锌溴液流电池为例,应用经典的安时积分法,测试得到一个完整的SOC周期,如图2所示。

图1 锌溴液流电池电解液的实测温度

图2 应用安时积分法得到的锌溴液流电池实际SOC数据
从图2 可以看出,在锌溴液流电池放电后期,其SOC 出现了明显的波动(红色虚线内),这预示着此时进入电压拐点阶段,这一点也可以由图3 来说明。此时需要从电压、电流采样与数据处理2 个层面进行改进,兼顾电解液流速与温度的影响,据此提高此时SOC的辨识精度。
图4所示为锌溴液流电池输出电压与母线电压的对应关系。从图4 可以看出,精确的SOC 辨识对提高液流电池的输出效果十分重要。与图2 相对比,可以发现,在放电后期SOC 出现非线性变化时,此时无论是锌溴液流电池的输出电压还是其对应的母线电压均出现了显著的波动(绿色虚线框内),这对为负载提供稳定的供电电压是不利的。
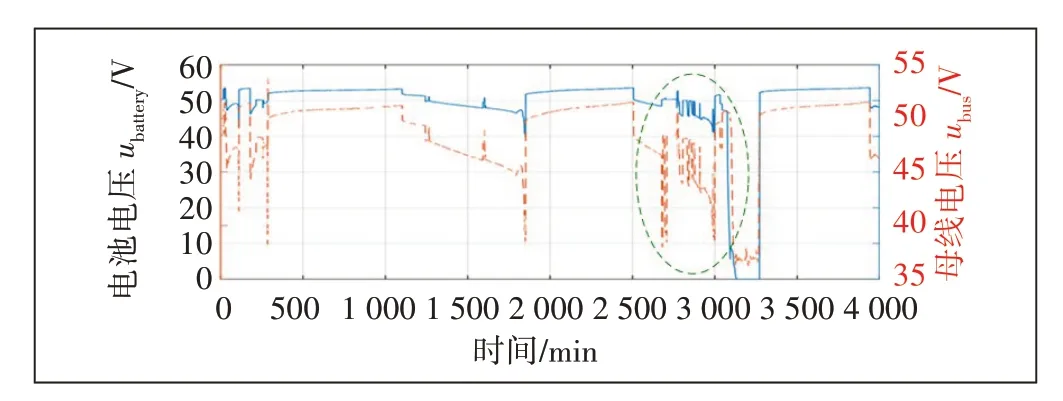
图4 锌溴液流电池输出电压与母线电压的对应关系
从电化学放电原理角度出发,液流电池放电后期的电压拐点是不可避免的,因此亟需从算法及数据处理角度进行校正,具体提供电压拐点处锌溴液流电池的供电效果,为其输出稳定的电压提供参考,PCA 算法的提出正是基于这一研究。综上,设ubattery、ibattery分别为锌溴液流电池的输出电压与电流;v、T、P分别为电池电解液的流速温度与压力,设输入样本元素为:
则SOC计算的PCA算法步骤总结如表1所示。

表1 SOC计算的PCA算法步骤总结
4 锌溴液流电池SOC实验计算分析
本文的实验条件如下。
a)所采用电池为合作企业所研发的10 kWh 锌溴液流电池,输出电压为DC 48 V,在100%充放电状态下满负荷运行,并直接并网。
b)电池的工作效率为82%左右,包括锌溴液流电池自放电电量损失。
c)实验的侧重点在于研究所提PCA 算法对锌溴液流电池放电后期电压拐点处SOC计算精度的影响。
d)图5 所示为锌溴液流电池充放电电压电流测试数据,在电压电流线性变化部分采用经典的安时电流法计算SOC、在放电后期非性变化部分采用PCA 进行特征提取与参数校正。

图5 锌溴液流电池充放电电压电流测试数据
设锌溴液流电池的输出电压、电流分别为ubattery与ibattery,则从图5 的实验数据可以看出:充电期间锌溴液流电池的电压与电流均处于线性变化状态;放电电压与放电电流在电池放电后期出现了显著的波动,即出现了放电拐点;电压与电流拐点造成采样数据的失真及数据丢失,亟待PCA处理。
实测表明,锌溴液流电池采样数据x中包含18 维特征值,但是其中包含很多无显著特征的信息(表现为电压拐点处尖峰数据的丢失)。如图6所示,对所有数据应用表1 中的算法进行PCA 分析,将18 维特征值降维至2维,结果显示,部分维度特征值并不含有重要信息,可以不进行采集、传输、存储。

图6 主成分分析法处理结果
为进一步处理SOC 参数辨识,最大可能突出电压拐点处信息,对数据做相关性分析,所得皮尔逊相关系数热图、斯皮尔曼相关系数热图及肯德尔秩相关系数热图如图7 所示。由上述分析可知,锌溴液流电池采样数据多维特征值中只有部分含有有用的信息,且与SOC 相关的特征值更少,因此可将与SOC 相关的参数划分为以下几类:电压值、电流值、温度值、电解液流速等。
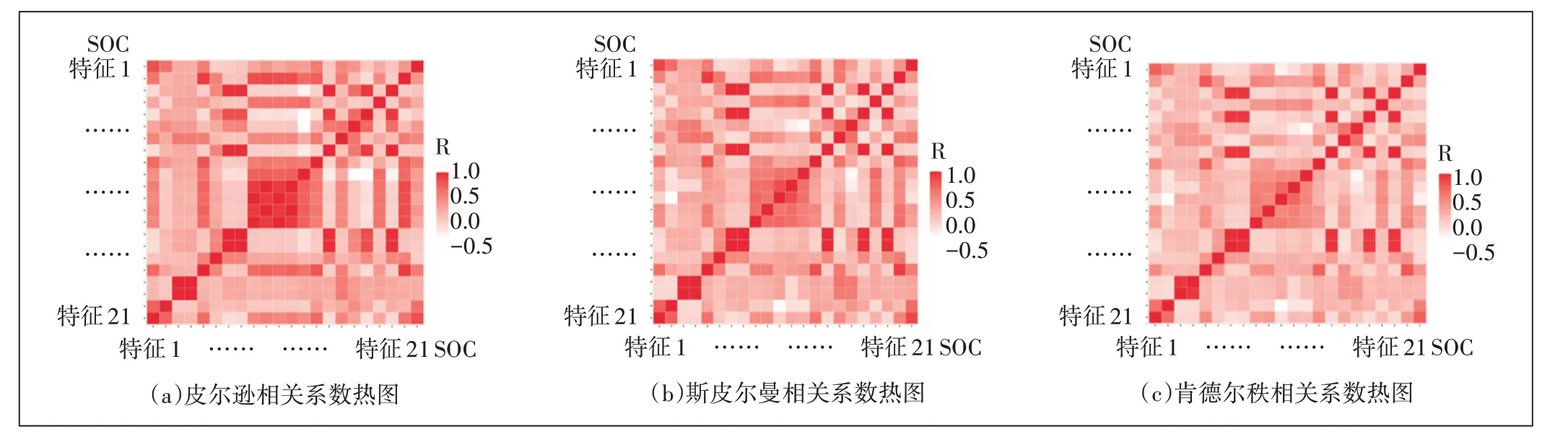
图7 相关系数热图
如图8 所示,可以将一次充放电过程中的电压变化划分为3 个部分:充电区间、放电区间1、放电区间2。充电区间与放电区间2电压变化呈线性,使用安时积分法计算SOC。而放电区间1(电压与SOC 关系如图9所示)电压变化激烈,如果使用安时积分法进行计算,则由于急剧变化的电压值导致采样精度无法得到保证,因此需要采用PCA 算法对锌溴液流电池SOC 进行评估与校正。

图8 锌溴液流电池电压曲线
图10为应用PCA 所得锌溴液流电池SOC数据,其中蓝色实线为整个充放电周期内采用安时积分计算得到的SOC 值、红色虚线采用所提分段PCA 处理得到的SOC 曲线。与图8 相比,虽然在放电拐点存在急剧的电压变化,但经PCA 数据处理所得SOC 曲线(红色虚线)与完全安时积分(蓝色实线)相比相对平滑,有效克服了放电后期电压拐点对SOC评估的影响。

图10 应用PCA所得锌溴液流电池SOC数据
表2所示为应用PCA算法校正前后的SOC误差分析,以校正后的红色虚线为基准,可以发现在(t1-t2)时段,PCA 校正后的SOC 曲线为线性变化,相对于采用安时积分法所得蓝色曲线,SOC 的最大计算误差可达20%,由此可见采用PCA 可有效降低电压拐点对锌溴液流电池SOC 计算的负面影响。综上,在锌溴液流电池电压拐点、及电压电流传感器发生采样失真的情况下,PCA 可以校正输入数据呈现训练过程中未出现的分布而产生的误差,可使SOC 估计误差维持在允许的范围,满足锌溴液流电池高精度SOC辨识需求。

表2 应用PCA算法校正前后的SOC误差分析
5 结论
本文提出了一种适用于锌溴液流电池放电后期电压拐点条件下的基于PCA 算法的电池荷电状态估计策略。能够在降低由于锌溴液流电池自身特性导致的较大SOC 估计误差的同时,在一定程度解决放电后期电压拐点导致的采样失真与数据丢失对SOC 估计的影响问题。可实现锌溴液流电池电压非线性区间的SOC 精准估计、减小实测数据采样噪声造成的较大SOC 估计误差。所提方法可通过高精度SOC 评估促进锌溴液流电池在长时储能场景下的工程应用,为实现大规模液流电池储能系统的均压与均流等优化控制提供参考。
