面积公式的由来与推导

顾卿璇

小学数学中求正方形、长方形、平行四边形、梯形和三角形的面积时都有具体的公式可以运用。例如，三角形的面积公式是“长× 高÷2”，而梯形的面积公式则是“（上底＋下底）× 高÷2”。那么，为什么会有这些求面积的公式呢？换言之，这些面积公式是怎么来的呢？

要弄清楚这些问题，就必须从根本上弄清楚“平方”概念的由来以及不同几何图形之间的联系。

一、面积公式的由来

数学上，面积单位一般是以“平方米”“平方厘米”“平方千米”（平方公里）来表述的。那么，什么是“平方”？或者，“平方”究竟是什么意思？

“平方”这一概念的起源可以追溯到古希腊数学中的平方数概念。古希腊数学家毕达哥拉斯和他的追随者首次研究了平方数的特性，即“一個数与自身相乘的运算”。

汉语中的“平方”的译文则来自英文的square，即“平方”也就是一个正方形面积的大小，因为square 的本义就是“正方形”。正方形的四条边的边长都一样长，假定某个正方形的边长为“x”，则这个正方形的面积就是“x × x”，而“x × x = x2”。如果这个边长的单位是“4 米（metre）”，则这个正方形的面积为 “16 平方米（squaremetres）”，于是写作“16 m2”。

至此，不难发现，所谓“面积”，也就是以某个长度单位（例如：厘米）为基准，在一个平面上可以分割出多少个边长为1 厘米的正方形。如果能够分割出8 个边长为1 厘米的正方形，则这个平面的面积为8平方厘米；如果能够分割出10个边长为1厘米的正方形，则这个平面的面积为10平方厘米。

于是，求正方形面积的公式便产生了——“S = a × a = a2”。这里，“S”在英文里代表“表面积”（Surface area），“a”代表正方形的边长。

二、面积公式的推导

正方形的面积公式是求其他几何图形面积公式的基础。有了这个基础，人们就不难推导出求其他几何图形的面积公式。

这里，必须确定的是：所谓“面积”的“面”就是“平面”的意思，而任何平面图形都可以被概括为“二维图形”，一个维度是“长”，另一个维度是“宽”（有时，又被称作“高”）；所谓“面积”的“积”就是“两个维度的相乘之积”的意思。

面积，面积，原来如此！

以下是一些面积公式的推导。

1.长方形面积公式的推导

既然正方形的面积是由边长与边长的乘积而得来，那么这就很好推导出长方形的面积计算公式了，因为正方形就是一个特殊的长方形。

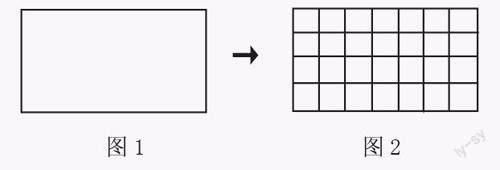
图1是一个边长7厘米、宽4厘米的长方形，那么怎么计算其面积呢？实际上，这并不困难，只要将其划分为边长为1厘米的正方形，然后数一数有多少个边长为1厘米的正方形，即可求出其面积。

于是，我们可以把图1转换成图2。

这样，我们就可以得到28个边长为1厘米的正方形，而1个边长为1厘米的正方形的面积为1平方厘米（1 cm2），那么28个边长为1厘米的正方形的面积自然是28平方厘米（28 cm2）。

用数学的算式来表达是“7 × 4 = 28 cm2”，因为每一行有7 个边长为1 厘米的正方形，每一列有4 个边长为1 厘米的正方形。

于是，长方形的面积计算公式：面积= 长× 宽。

2. 平行四边形面积公式的推导

明白了长方形的面积公式的推导过程，人们就不难得出平行四边形面积公式的推导。

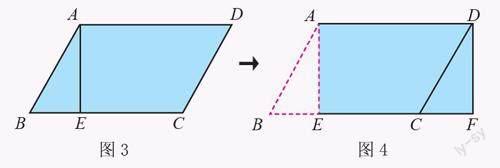
图3 是一个边长3 厘米、高2 厘米的平行四边形，怎么才能求出其面积呢？

由于平行四边形具有对应边平行、对应边长度相等的特性，那么就可以过A 点作垂线交BC 于E，分割出RT △ ABE。然后，运用“平移”（rotation）的原理，将RT △ ABE 平移到DCF 的位置，就可以得到一个长方形，且所得到的这个长方形的上底与下底的边长没有变化，高也没有变化，因此面积大小也不会变化。

既然长方形的面积计算公式是“面积 =长× 宽”，那么平行四边形的面积不就是“底边边长× 高”吗？而通过观察和对比图3 向图4的转换，我们就可以发现 ：平行四边形的“底边边长”就是长方形的“长”，平行四边形的“高”就是长方形的“宽”。

3. 梯形面积公式的推导

图5 是一个上底2 厘米、下底4 厘米、高3 厘米的梯形。如何求其面积呢？实际上，求平行四边形面积的“割补法”对推导梯形面积的公式具有启示作用。

我们只要分别过A点作垂直于BC的垂线于G和过D点作垂直于BC的垂线于H，然后分别取BG的中点F和HC的中点I作垂线EF交于E和垂线JI交于J，再将△JIC逆时针旋转180°，至△DJK的位置，将△EBF顺时针旋转180°，至△ALE的位置，就可以得到一个长方形LFIK。

因为：AD = GH， BF = FG = LA， HI = IC = DK，

所以：LA + AD + DK

= FG + GH + HI

= （AD + BC） ÷ 2

= （2 + 4） ÷ 2

= 6 ÷ 2

= 3

于是，“3厘米”即长方形LFIK的“长”，那么这个长方形的面积就是9平方厘米（3×3 = 9）。而长方形LFIK的“长”由梯形的“（上底+下底）÷2”得来，至此梯形的面积公式就被推导出来了——面积=（上底+下底）×高÷ 2。

4.三角形面积公式的推导

三角形面积公式的推导，似乎比长方形、平行四边形和梯形的面积公式的推导要复杂一些，其实不然。

最简单的办法是，当你把一张正方形的纸沿着其中一条对角线剪开，你就能够得到两个面积一样大的三角形。如前所述，正方形的面积是“边长与边长的乘积”，那么你所得到的三角形的面积不就是正方形面积的一半吗？

同样，当你把一张长方形（见图7）的纸沿着其中一条对角线剪开，你也能够得到两个面积一样大的三角形。而长方形的面积是“AB × AC ”，那么三角形的面积不就是这个长方形的面积除以2 吗？而△ BCD 的“底”（CD）就是原来的长方形的“长”，这个三角形的“高”（BD）就是原来的长方形的“宽”，那么，三角形的面积公式不就是“（长× 宽）÷ 2”吗？

三、结论与启发

通过对面积公式的由来与推导的讨论，我们至少可以得出这样的结论：面积公式的根本是正方形的面积公式，求几何图形面积的关键是确定二维图形的两个维度，或表现为“长和宽”，或表现为“底和高”。同时，我们从中也可以得到启示，即数学知识是一个相互联系的整体，因此在运用数学知识解决问题时要有联系的、系统的观念。