斜拉桥索塔锚固区应力及优化分析

赵丹　冯煜

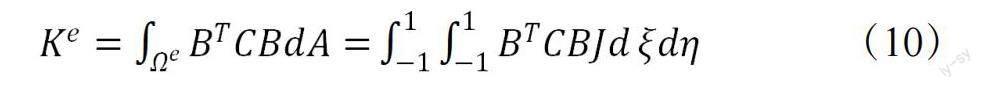
摘要 大跨度斜拉桥高速发展下，索塔承受的索力也越来越大，这就对索塔锚固区构造提出了更高的要求。索塔錨固区是斜拉桥的关键部位，拉索的集中力将通过这一部位安全、均匀地传递到塔柱中。因此，斜拉桥索塔锚固区受力性能一直以来受到桥梁界的关注。以乌江特大桥为实例，利用有限元软件Abaqus建立索塔锚固区局部空间精细有限元模型，分析环向预应力和索力作用下索塔的混凝土应力变化。

关键词 桥梁工程；斜拉桥；索塔；应力状态

中图分类号 U441.5文献标识码 A文章编号 2096-8949（2023）24-0128-04

0 引言

索塔在斜拉桥结构当中起着重要的桥梁负荷承载任务，正常运行主要需要承受桥梁面的索力与荷载及其本身的重量。索塔锚固区也是主梁锚固和索塔锚固的区域，主要承受整座斜拉桥的重量，所以重点研究斜拉桥索塔锚固区应力及优化有现实意义。

1 斜拉桥索塔锚固区的应力结构和分析方法

1.1 结构特点

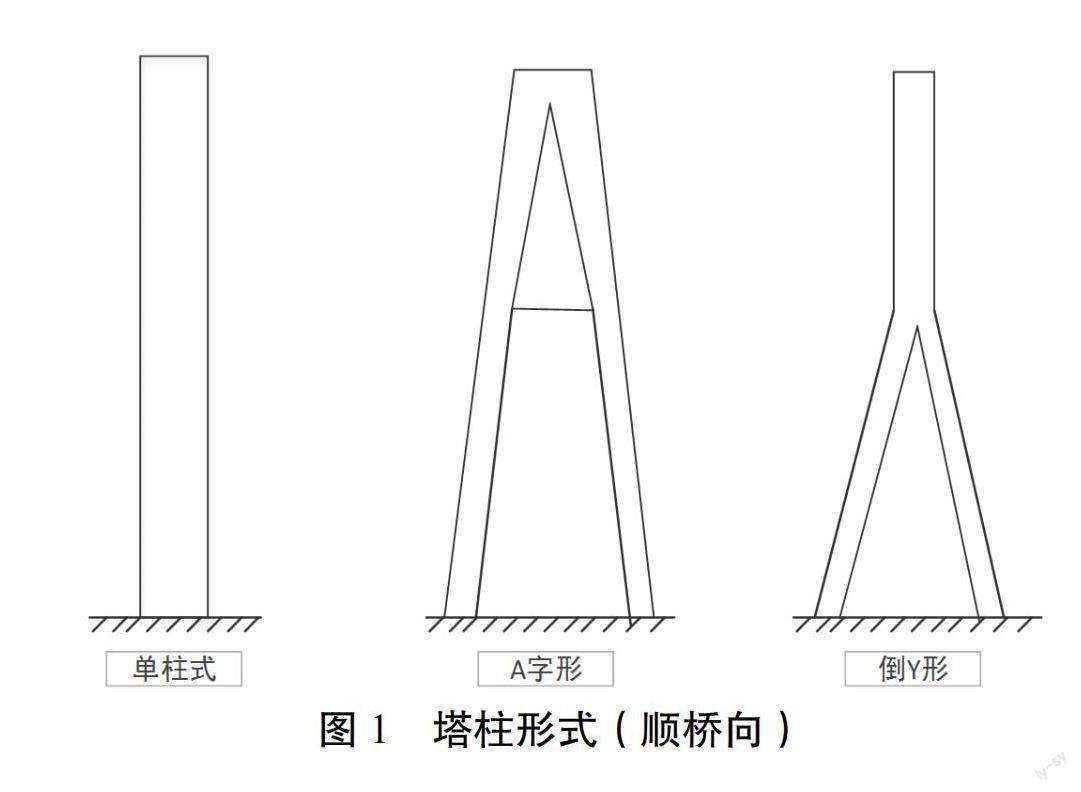
从顺桥来看，一般结构形式有以下形式，具体见图1。

从横向来看，主塔形式主要包括以下几种形式，具体见图2。

1.2 计算方法

1.2.1 理论计算方法

该方法中包含了力学解析法和数学解析法，把该方法应用在斜拉桥索塔锚固区域的应力分析当中，借助各种解析工具，创建相应的力学模型，比如通过极限平衡方法、弹性力学方法以及杠件分析方法计算分析索塔锚固的应力情况[1]。

1.2.2 有限分析方法

如今土木工程和结构工程中研究应用效率最高的方法之一——有限分析方法，此方法结合结构分段进行建模，深入分析每个部分的材料特性和力学特性，借助先进软件有效模拟和计算结构应力。在斜拉桥索塔锚固区域应力分析中，合理使用有限元分析法最终的计算结果非常理想，需要结合桥梁结构特点创建模型，同时用有限元分析软件建构模型。最终在模型数值结果分析中计算出斜拉桥索塔锚固区的应力情况。

2 实际案例分析

2.1 项目概况

该文主要分析了乌江特大桥结构应力分析，该桥梁主体结构主要为135 m+300 m+135 m的双塔斜拉桥，其中P5桥塔和P6桥塔均为H形塔，且组成部分还包括了2道横梁与上、下2个塔柱，横梁与上下塔柱基本使用了C55混凝土，上下塔柱一般为普通钢筋混凝土结构，上下横梁均为预应力混凝土结构，此桥梁索塔锚固区主要形式将布设为U形环向预应力。对于斜拉索一般会使用Ф7 mm镀锌高强度、低松弛平行钢丝HDPE 护套成品索，其抗拉强度不会小于1 770 MPa，与此同时满足斜拉索基本施工要求。针对乌江特大桥预应力分析，将合理应用有限元分析法[2]。

2.2 有限元分析

斜拉桥索塔有限元模型创设分析。

2.2.1 有限元模型结构

结构材料参数具体见表1。

2.2.2 模型单元类型

针对该模型进行有效分析，在分析中会使用Abaqus软件，并通过其中的8节点六面体线性减缩积分单元（C3D8R）集中解析混凝土状况，针对实体单元基本使用同性材料。其中缩减积分单元定义为每个方向都比完全积分单元少一个积分点。采用减缩积分的二维单元积分点可见图3。

线性减缩积分单元主要是沙漏数值问题的存在，因此该单元中心将会积累一个积分点，而积分单元当中的虚线长度变化并不明显，且夹角也是原本模样，体现了该单元中的积分全部预应力数值为零。由于单位变形无应变能力，因此这样的弯曲模式属于一个零能量模式。由此可见，单元在此模式下并不存在刚度，所以单元不能承受变形情况。基于粗划网格模式，这样的零能量模式会在网格中不断拓展，进而形成无意义结果。对沙漏现象的分析如下：

式中，uiI——节点上的位移；xiI——节点坐标；——形函数；=（1，?1，1，?1），ηI=（1，?1，1，?1），小写下标代表方向，大写下标代表的是节点（x1，x2）=（x，y）。

动量方程表示为：

有效使用伽辽金分析方式，借助虚位移原理基于单元积分而得到：

其中：

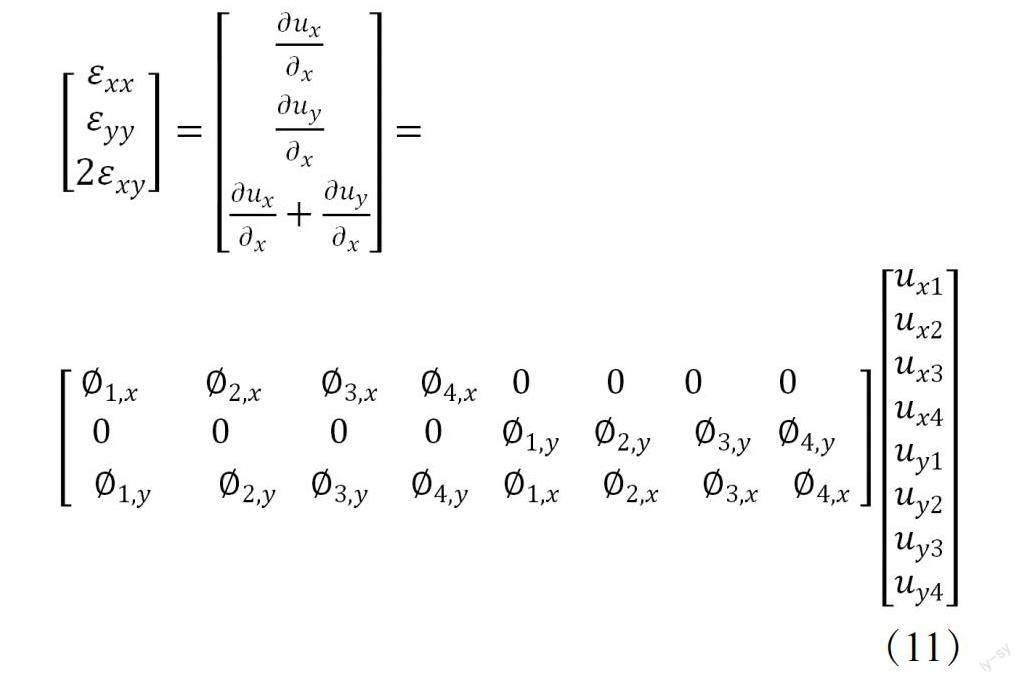
针对（6）式中的积分将使用节点集中质量，简化计算过程。而（8）式积分主要由边界条件决定；对（7）式将使用一点高斯积分。针对弹性材料，该结构表示为C，并将（7）式张量转变为列矢量，其公式表示为：

其中：

这里B矩阵的表达式为：

简记为：

单元刚度矩阵表示如下：

式中，n表示为高斯积分点数，当n=1时，则积分为1点，1点积分的高斯点表述为，其刚度矩阵则表示为：

能够快速计算出1点积分的有限元刚度矩阵表示为：

基于二维平面运动，其刚度矩阵表示为：

式中，nRB——刚度数目，也就是刚度矩阵零子空间维数。二维模式下，一共存在3种刚体运动，如刚体旋转运动、两个方向的平移，也就是刚度矩阵存在2秩的缺陷，这也是产生沙漏情况的本质原因。弯矩作用下减缩积分线形单元的变形见图4[3]。

在该次的斜拉桥应力分析中，利用沙漏刚度分析法，能够有效控制线性减缩积分单元沙漏扩散问题，网格数目越多，则限制效果越好。这样的线性减缩积分单元具有以下特点：其一，能够精准求解位移问题；其二，重点分析精度不受限于网格变形；其三，如果存在弯曲荷载问题，也不会出现自锁情况。因为这些特点与优势，该次分析使用C3D8R实体单元划分混凝土模型与聚合物砂中的有限元网格。

基于Abaqus软件分析，通常会运用Rebar定义以及嵌入单元方法来对混凝土当中的加强筋模型进行创建，在这之中，Rebar本身不存在尺度，和一维应变理论杆单元相同，并不属于单元，而是某一平面内进行成批或者单个的定义。通常情况下，会在多种类型的单元中嵌入金属塑性的Rebar，并使用Rebar方法有效定义混凝土中的加强筋，一般常被认为与混凝土行为是分开的。但是在实际的模型建设中，必须结合捆绑移动和销子效应，这样能够很大程度上提升模型作用，同时应用拉伸强化法，通过Rebar穿过裂纹，完成荷载传递[4]。现阶段的Abaqus分析版本中，CAE模块无法显示Rebar。

2.3 计算结果

2.3.1 仅施加环向预应力

当只对桥梁实施加环向预应力时，C50混凝土标准抗拉强度2.65 MPa，混凝土应力基本在?2.2～3.9 MPa之间。混凝土第3主应力基本在?14～?0.1 MPa之间。应力范围基本在?7～0.2 MPa之间，齿块出现小范围拉应力，约0.7 MPa。横桥向应力范围基本在?14～1 MPa之间。齿块出现小范围拉应力，约0.7 MPa[5]。

2.3.2 索力+环向预应力

当施加索力及环向预应力时，C50混凝土标准抗拉强度2.65 MPa，混凝土应力基本在?3.5～4.5 MPa之间。混凝土第3主应力基本在?23～?0.1 MPa之间。混凝土纵向应力分布范围基本在?10～0.6 MPa之间，齿块未出现拉应力。混凝土横向应力范围基本在?20～0.9 MPa之间，齿块未出现拉应力。

2.4 主要创新点

在该次分析中，无论是有限元分析，还是实际试验设计，都严格按照预期设计图纸当中的斜拉索角度进行施工，优化设计索力，确保桥面受力和预期结果接近。在实验斜拉桥索塔锚固区模型中，高度重视实验阶段的高度，在实际分析中选取同一个桥梁模型中同样的预应力荷载、斜拉索索力进行详细的有限元模型创建，探索塔柱的整体应力状态。索力调整施工方案的具体实施见图5。

3 结论

分析过程中，保证混凝土中的第一主应力都在预期范围内，其应力数字偏大区域也将集中在26号和27号齿块区域；当只对桥梁进行环向预应力施工时，26号和27号齿块区域第一主应力会在2.8 MPa以内，对其实施索力之后，26號和27号齿块区域第一主应力在4.3 MPa以内，混凝土第3主应力均在规范限值内。仅施加环向预应力时，齿块区域出现纵桥向及横桥向拉应力，在0.7 MPa以内，施加索力后，齿块应力状态良好，未出现拉应力。该次分析的桥梁索塔锚固区应力集中范围较小，主要出现在齿块部分，施加环向预应力能够较好地减少斜拉桥主塔的应力集中问题，改善索塔受力情况。

参考文献

[1]熊礼鹏， 陈泉， 刘峰. 独塔斜拉桥索塔锚固区承载力分析[J]. 市政技术， 2022（7）： 160-163+168.

[2]袁锋. 银洲湖特大桥索塔锚固区域受力状况分析[J]. 科学技术创新， 2022（33）： 110-113.

[3]郑万山， 李双龙. 桥梁伸缩缝锚固区应力响应及参数优化研究[J]. 公路交通技术， 2022（6）： 43-50.

[4]李健刚， 杨冰. 斜拉桥异形钢索塔锚固区受力敏感性因素分析[J]. 桥梁建设， 2023（3）： 64-70.

[5]成新， 周慧. 基于有限元模型的斜拉桥索塔锚固区预应力效应分析——以泸州白沙长江大桥为例[J]. 工程技术研究， 2023（6）： 1-5.