基于MSEIR城市轨道交通网络拥挤消散研究

周中懿

摘要 城市轨道发展迅速，从单线到成网为出行者提供便利，随着城市轨道交通网络可达性的上升逐渐成为出行者城市内部出行的主体。社会发展使得大型活动规模越发庞大、频率越发频繁，在大客流冲击下原有设施设备无法承担大客流压力，导致站内区间拥堵愈发严重，拥堵影响范围由单线向网络蔓延。为更好地应对客流压力，分析拥挤传播机理有着重要意义。以某轨道交通网络为例，考虑站点自身属性以及受大客流辐射影响情况，构建MSEIR客流拥挤传播模型。并与传统SIR、SEIR模型结果对比，探索更合适的客流拥挤传播规律，为轨道交通运营方客流管控提供理论依据。

关键词 大客流；拥挤传播；传染病模型；元胞自动机

中图分类号 U293.13文献标识码 A文章编号 2096-8949（2023）24-0038-04

0 引言

轨道交通立体化的发展使得轨道交通网络日益复杂，在客流冲击下客流拥堵范围更广，传播路径更多样，扩大了拥堵客流影响面积，严重威胁运营方与出行者的安全。因此，分析客流拥堵传播机理，研究拥堵客流对城市立体轨道交通网络影响程度的深浅与范围的大小，对城市立体轨道交通的运营及优化具有重大意义。国内外学者对突发客流传播机理进行了相关研究，针对城市轨道交通内部的客流传播机理，目前学者主要通过大数据方法和仿真方法对不同层面的客流传播规律进行研究。虽取得一定成果，但对于城市轨道交通突发大客流传播仍存某些不足，主要体现在对客流以及服务网络的考虑过于简化；对站点状态划分非0即1，未能反映站点的多样化差异；演化规则过于简单，模型准确性不够[1]。为解决以上问题，该文以某城市轨道交通网络为例，基于经典传染病理论，通过对实际不同位置的站点客流承载情况，对站点的状态演化方式进行确定，进而得出MSEIR城市轨道交通网络拥挤消散模型。

1 基于图元胞自动机的仿真环境构建

元胞自动机基本可分为元胞、元胞空间、邻居及演化规则4部分，可用一个四元组表示：CA={Ld，S，N，f}，其中，Ld代表元胞空间，d代表空间维数，S为元胞的有限状态集，N表示一个所有邻居内元胞的组合，包括中心元胞在内，是包含n个不同元胞的空间矢量，n为邻居元胞个数，F表示局部转换函数[2-3]。元胞状态的变化依赖于自身及邻居的状态，且某个元胞下一时刻的状态只取决于邻居的状态以及自身的初始状态。

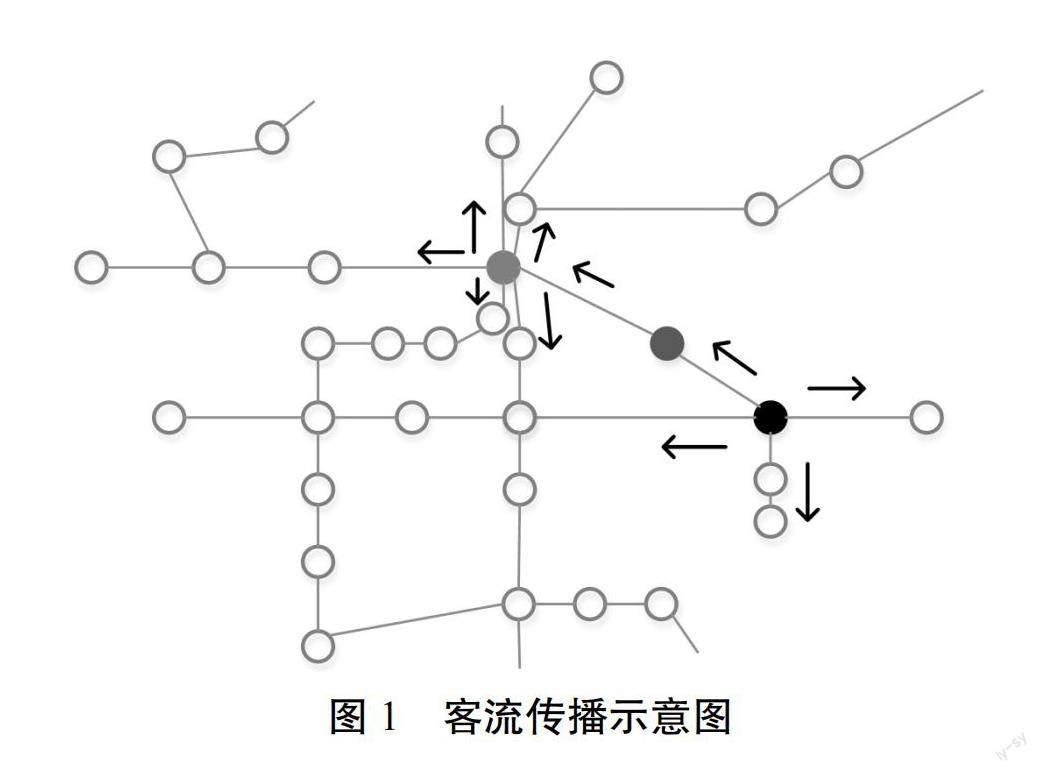
突发客流造成的拥挤传播是以客流源最近的交通站点作为中心，通过运行区间沿着线路结构在中间站继续传播，在换乘站向不同方向进行扩散的过程[4]，如图1所示。

定义lij为不同站点i与j的关系如下关系所示：

式中，lij，i，j——站点编号。当lij=1时，表示站点i与站点j之间存在链接互为邻居，即客流可直接在站点i与站点j之间通过一个区间传播；当lij=0时，表示不为邻居。

站点状态有四种：正常、潜伏、拥挤、恢复。用来表示t时刻元胞i所处状态，状态空间为{0，1，2，3}分别对应这四种状态。考虑不同车站的地理位置以及客流承载能力不同，站点会有不同的狀态演化方式，该文在传统SEIR模型基础上考虑这种因素得到改进的传染病模型，把这个改进的传染病模型称之为MSEIR模型。MSEIR中不同类型的站点以及演化方式如表1、图2所示。

在这种拥挤客流传播模式下，城市轨道交通各个车站在时刻t下的状态集Qt可表示为Qt=（St，Et，It，Rt ），其中，St，Et，It，Rt分别为时刻t下城轨网络内处于正常状态（S）、潜伏状态（E）、拥挤状态（I）以及恢复状态（R）的车站的比例。故在任意时刻t与其下一时刻t+Δt（Δt为仿真中一个时间步的步长），都有：

St+Et+It+Rt=St+Δt+Et+Δt+It+Δt+Rt+Δt=1 （2）

对于下一时刻（t+Δt），网络中各个状态车站的比例可用下述公式表示[5]。

其中，正常状态S车站的比例为：

其中，正常状态E车站的比例为：

其中，正常状态I车站的比例为：

其中，正常状态R车站的比例为：

式中，Sts、Ets、Its、Rts——t时刻演化状态为（S→E→I→R）的四种状态的元胞比例；λs、φ、εs——该类元胞的拥挤传播率、潜伏率、拥挤消散率；Ste、Ete、Rte——t时刻演化状态为（S→E→R）的三种状态的元胞比例；λe、εe——该类元胞的拥挤传播率，拥挤消散率；Sti、Iti、Rti——t时刻演化状态为（S→I→R）的三种状态的元胞比例，λi、εi——该类元胞的拥挤传播率，拥挤消散率；Str、Rtr——t时刻演化状态为（S→R）的两种状态的元胞比例，εr——该类元胞的拥挤消散率；

2 仿真及其结果分析

2.1 NetLogo仿真软件简介

NetLogo是一种用于建模和仿真复杂系统的程序设计语言和环境，其丰富的内置函数和命令，使用户能够轻松地控制模型的行为和演化。用户可以通过可视化的界面对模型进行设计和调参，并可以通过编写NetLogo代码来自定义模型的行为。NetLogo支持外部数据软件集成，可以实现对不同的现象及其过程重现演示，由于NetLogo研究复杂的系统行为和模式的强大功能，被广泛用于如城市交通、社会网络和生态系统等领域。

使用NetLogo建模一般包括以下步骤，如图3所示。

2.2 仿真结果分析

以某城市轨道交通网络为该文研究的拓扑结构模型，模型的仿真步骤为：

Step0：仿真系统原始状态。输入交通网络站点线路拓扑数据。对网络内的所有站点进行演化方式设定设置，初始化状态为0。

Step1：初始化拥挤节点以及时间步。

Step2：设置潜伏站点与恢复站点的数为0。

Step3：根据前文规则对节点初始化个体状态演化方式。

Step4：判断站点邻接，进行站点状态更新。

Step5：分别统计时间步t下，城市轨道交通网络中集内状态车站的数量。

Step6：当城市立体交通网络内状态为1和2的数量为0时，仿真结束，输出仿真结果。

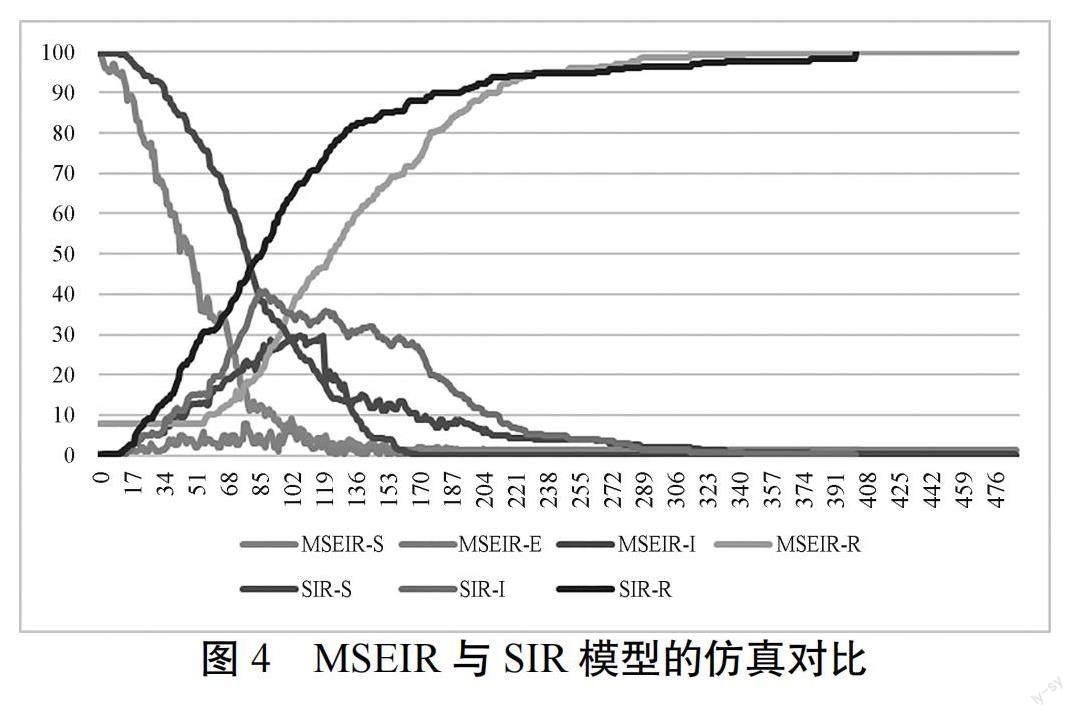
城市轨道交通网络仿真结果如图4所示。

图4可以看出，从拥堵传播周期上来看，SIR周期时间要短于MSEIR周期时间，这是由于站点状态的增加，站点演化总周期也会相应增加。从正常站点上来看，MSEIR模型输出结果正常站点变化要快于SIR模型结果，这是由于MSEIR模型正常站点的演化方式要多于传统SIR模型。从拥挤站点上来看34时间步之前二者结果相似，这是由于突发大客流发生源周边较近站点客流承载能力远不能承载突发大客流的客流量，所以MSEIR模型中，这类站点会与SIR的演化方式一致。从拥挤站点峰值上来看，MSEIR的峰值要低于SEIR的峰值，这是由于部分站点客流缓解能力较强，并且距离突发大客流源不近，受到突发大客流的辐射较小，这类站点在演化过程中会受客流影响变为潜伏状态，但由于其客流消散能力较强，所以会直接从潜伏状态转变为恢复状态。从恢复站点来看MSEIR输出结果，在拥堵传播前期是高于SIR模型的，这是由于部分边缘站点不会发生拥堵情况；中期的输出结果低于SIR模型，这是由于对于MSEIR站点而言，由正常状态转变为恢复状态需要更多的过程。后期输出结果要高于SIR模型，这是由于前期远端站点已经演化为恢复状态，所以在后期免疫站点变化幅度不大的状态下MSEIR模型的恢复状态站点输出会高于SIR模型。

如图5所示，从拥堵传播周期上来看，MSEIR模型的周期时间为487时间步，SEIR模型的周期时间为484，时间步差别不大。从正常站点上来看，MSEIR模型输出结果正常站点变化要快于SEIR模型结果，这是由于MSEIR模型正常站点的演化方式要多于传统SEIR模型。从潜伏站点上来看，传播前期二者结果相似，中后期由于站点状态演化方式不同，SEIR的潜伏站点输出数据要高于MSEIR输出结果。从拥挤站点上来看，由于突发大客流发生源周边较近站点远不能承载突发大客流的客流量，所以MSEIR仿真结果在前期要高于传统SEIR模型；在后期且离突发大客流源较远的站点受到客流影响较小时，部分站点会从潜伏状态直接演化为恢复状态，所以MSEIR的峰值要低于SEIR的峰值。从恢复站点来看MSEIR输出结果高于SEIR模型输出结果，原因与MSEIR和SIR的恢复站点原因一致。可以看出，在城市轨道交通突发大客流拥挤消散上来看，MSEIR相比于SEIR和SIR模型能够更好地与实际符合。

为了进一步研究城市轨道交通客流拥堵传播模型中各参数对传播范围的影响，对其进行仿真分析，结果如下。

拥挤传播率取值0.12、0.22、0.32、0.42、0.52，不同拥挤传播率对拥挤传播范围的影响如图6所示。

从图6可以看出，随着拥挤传播率由0.12提升到0.52，从整体趋势上来看拥挤站点输出结果均为先上升达到峰值再下降，拥挤传播率越大拥挤站点总体增加速率越大。从峰值上来看，拥挤传播率越大城市轨道交通网络拥挤站点数目越多，传播范围更广。

拥挤消散率取值0.2、0.3、0.4、0.5、0.6，不同拥挤消散率对拥挤传播范围的影响如图7所示。

从图7可以看出，随着拥挤消散率由0.2提升到0.6，从整体趋势上来看，拥挤站点输出结果均为先上升达到峰值再下降，拥挤消散率越大达到拥挤站点峰值的时间越短。从峰值上来看，拥挤消散率越大拥挤站点数目越少，传播范围更小。

初始拥挤站点设置为2、4、6、8，不同初始拥挤站点对拥挤传播范围的影响如图8所示。

从图8可以看出，初始拥挤站点对拥堵站点数量极值点的影响较小，拥堵传播范围均为35%～40%。而随着初始拥挤站点数目增加，拥挤站点输出极值点的时间越少。达到极值点之后拥挤站点演化为恢复站点的趋势和速率几乎一样。

3 结论

為了对轨道交通拥挤传播进行研究，该文研究了经典城市轨道交通传染病模型。正确认识产生城市立体交通突发事件无干预措施下的动态拥挤传播过程，是制定应急干预措施、妥善控制城市立体交通网络拥挤客流的基础，这对运营方更好制定管理措施以应对突发大客流的影响具有借鉴意义。该文基于经典传染病模型，考虑站点异质性与受客流辐射强弱，提出了MSEIR传播仿真模型，并对拥挤传播率、拥挤消散率、初始拥挤站点个数进一步分析。分析表明，初始拥挤站点数目对拥挤传播整体而言影响不大；拥挤传播率影响城市轨道交通网络拥挤站点达到峰值的速率；采取适当措施，增加拥挤消散率才能有效缓解城市轨道交通网络的拥堵问题。下一步将结合具体AFC数据量化拥挤传播参数分析不同时间段的拥挤传播情况。

参考文献

[1]徐欣怡. 列车运营故障条件下客流拥挤传播特性及疏导策略研究[D]. 江苏：南京理工大学， 2021.

[2]段晓东， 王存睿， 刘向东. 元胞自动机理论研究及其仿真应用[M]. 北京：科学出版社， 2012.

[3]李学伟， 吴今培， 李雪岩. 实用元胞自动机导论[M]. 北京：北京交通大学出版社， 2013.

[4]蒋阳升， 刘纹滔， 姚志洪. 基于元胞自动机的轨道交通突发客流拥堵消散演化机理研究[J]. 交通运输系统工程与信息， 2020（5）： 121-127.

[5]王兴川. 基于出行行为分析的突发事件下城轨客流拥挤传播研究[D]. 北京：北京交通大学， 2020.