基于多层感知器和SAR参数的海浪有效波高反演方法*

高亚飞, 王运华,3**, 张彦敏, 姜文正

(1. 中国海洋大学信息科学与工程学部, 山东 青岛 266100; 2.自然资源部第一海洋研究所, 山东 青岛 266061;3. 青岛海洋科学与技术试点国家实验室 区域海洋动力学与数值模拟功能实验室, 山东 青岛 266237)

海浪是海洋表面最常见的现象,可以分为风浪和涌浪。海浪对海洋工程、海洋运输、海岸港口建设、海洋渔业以及沿岸居民的生活等都有重要影响,准确地获取海浪信息是海洋遥感领域的一个重要研究课题。目前,随着星载SAR技术的发展,大量的海面SAR图像数据为反演海浪信息奠定了数据基础。

通过SAR图像反演海浪信息的方法可以分为两类:基于物理的方法和经验模型。第一类是利用SAR图像反演海浪方向谱,进而获取海浪信息。对于单极化SAR数据,1991年Hasslamnn等[1]推导了SAR图像谱和海浪谱之间的非线性映射关系并提出了MPI方法。该方法基于初猜谱和SAR图像谱构建代价函数并最小化代价函数获取最优海浪谱。后来研究人员改进了MPI方法中的非线性映射关系并提高了运算效率[2-3]。2005年Schulz等[4]在MPI方法的基础上应用交叉谱提出了PASRA方法,这些方法都需要先输入初猜谱。然而初猜谱难以获取而且准确度较低,导致反演的海浪谱误差较大。2000年Lehner等[5]和Wan等[6]利用交叉谱反演海浪谱,这种方法较大程度上减小了散斑噪声,并且提供了海浪传播方向,而且Wan进一步研究了海浪能量密度分布。同时,多极化SAR数据海浪反演方法也有很大的进步,基于全极化SAR数据反演海浪斜率谱的方法被提出来[7-9],而且Shao的研究弥补了X波段数据反演海浪参数方法较少的不足[10]。2010年,Zhang等[11]在海浪斜率谱极化调制算法的基础上提出反演方位向和距离向斜率谱的方法。该方法消除了流体力学调制的影响,但是对小入射角数据效果较差。2020年YanminZhang等[12]利用多极化数据推导出一种新的海浪谱与SAR图像谱之间的非线性映射关系,并用经验化的倾斜调制函数替代传统的倾斜调制函数。虽然海浪谱能够获得较为完备的海浪信息,但是SAR图像谱与海浪谱之间的非线性映射关系复杂,难以通过SAR图像反演得到准确的海浪谱,尤其是风浪谱。

第二类是基于拟合的方法建立SAR图像参数与海浪信息之间的经验关系模型。2007年Schulz等[13]在CWAVE方法的基础上提出了CWAVE-ERS经验化算法,针对不同的卫星数据,研究人员分别提出了CWAVE_S1A算法[14],CWAVE_ENV算法[15]和XWAVE算法[16]。这些方法利用谱分解的方式从SAR图像谱中提取出20个与海浪信息相关的参数,然后将这些参数结合后向散射系数和图像强度归一化方差拟合出海浪有效波高。CWAVE方法在上面不同的SAR数据上的均方根误差不同,分别为0.5、0.5、0.39和0.25 m。研究人员逐渐发现截止波长与海浪有效波高之间的强相关性,并利用截止波长和其他参数反演海浪有效波高和平均波周期[17-21],模型反演海浪有效波高的均方根误差约为0.7 m。2021年Pramudya等[22]利用双极化SAR数据获取更加准确的截止波长并建立经验关系模型反演海浪有效波高,将均方根误差降低至0.59 m。2015年Romeiser等[23]针对极端海况下SAR图像中海浪特征模糊的问题,建立了后向散射系数与海浪有效波高之间的经验关系。2017年Lin等人利用新的地球物理模式函数反演海表面风速,然后利用反演得到的风速和PFSM函数获取海浪有效波高和平均波周期[24],该方法反演波高的均方根误差约为0.54 m。这些经验关系模型使用到的参数较少,而且公式模型的非线性拟合能力不足,导致海浪有效波高的反演精度较低。

近年来,随着海洋SAR数据量增加和机器学习技术的发展,越来越多的神经网络模型被应用于SAR图像信息挖掘[25-28]。在海浪有效波高反演方面,2018年Gao等[29]利用支持向量机模型和ASAR数据反演海浪有效波高,反演结果的均方根误差约为0.42 m。一些研究人员利用经典感知器模型和Sentinel-1数据反演海浪有效波高[30-31],模型反演结果的均方根误差约为0.53 m。卷积神经网络也逐渐被用于反演海浪有效波高[32-33],2022年Wang[34]等利用全极化SAR数据和卷积神经网络模型反演海浪有效波高,并分析了不同极化方式对海浪有效波高反演结果的影响。卷积神经网络模型将反演结果的均方根误差降至0.3 m,大大提高了海浪有效波高的反演精度,但是模型参数和模型训练时间也急剧增加。在过去的研究中,已有的感知器模型存在以下几个问题:隐层层数单一、对海浪信息挖掘能力不足;以往模型仅仅反演了整体海浪有效波高信息,并没有建立输出风浪效波高和涌浪有效波高的多输出模型;不同海况下的数据分布不均衡,尤其是高海况下数据量较少,这导致模型存在明显偏差,反演精度较低。

针对以上存在的问题,论文在分析SAR海面回波多个参数与海浪有效波高相关性的基础上,应用哨兵1A卫星数据中后向散射系数、图像强度归一化方差、截止波长、主波波长、主波波向、图像偏度和峰度参数,建立了基于多层感知器的海浪有效波高反演模型,该模型同时输出整体海浪有效波高、风浪有效波高和涌浪有效波高。同时,文中采用校正函数降低由于极端海况数据较少导致的模型偏差,增强了模型的适用性。最后将模型反演结果与匹配的ECMWF和Jason3卫星有效波高数据进行对比,检验了本文方法的有效性。

1 数据源介绍

文中共使用三种数据:哨兵1A卫星二级SAR数据、欧洲中期天气预报中心第五代再分析数据(ERA5)以及Jason3卫星高度计数据。

哨兵1A卫星是一颗搭载C波段合成孔径雷达传感器的极轨遥感卫星,该卫星发射于2014年4月,同年10月开始进行数据采集。哨兵1A卫星传感器包括四种成像方式,其中,波模式是观测海洋的默认模式,可以提供HH和VV极化的SAR图像数据,VV极化是波模式下默认的极化方式。SAR传感器沿卫星飞行轨道每隔100 km进行一次数据采集,以近似23 °(WV1)和36°(WV2)的入射角进行交替观测。卫星的重访周期为12 d。SAR图像的空间分辨率为4 m×4 m,图像大小为20 km×20 km。本文使用的SAR数据为二级波模式VV极化数据,其中包含:后向散射系数、图像强度归一化方差、截止波长、交叉谱、图像偏度和峰度等参数。

由于SAR图像容易受到其他海洋现象的影响,因此需要对SAR数据进行预筛选。在筛选过程中坚持两个原则:其一,为了避免海冰影响,筛选出的SAR图像位于南北纬60°之间;其二,根据SAR图像强度归一化方差对两个入射角的SAR图像进行筛选,图像强度归一化方差(NV)表征了SAR图像强度的均质性,通过设置阈值可以避免其他海洋现象的影响。NV的计算方式如公式(1)所示。

(1)

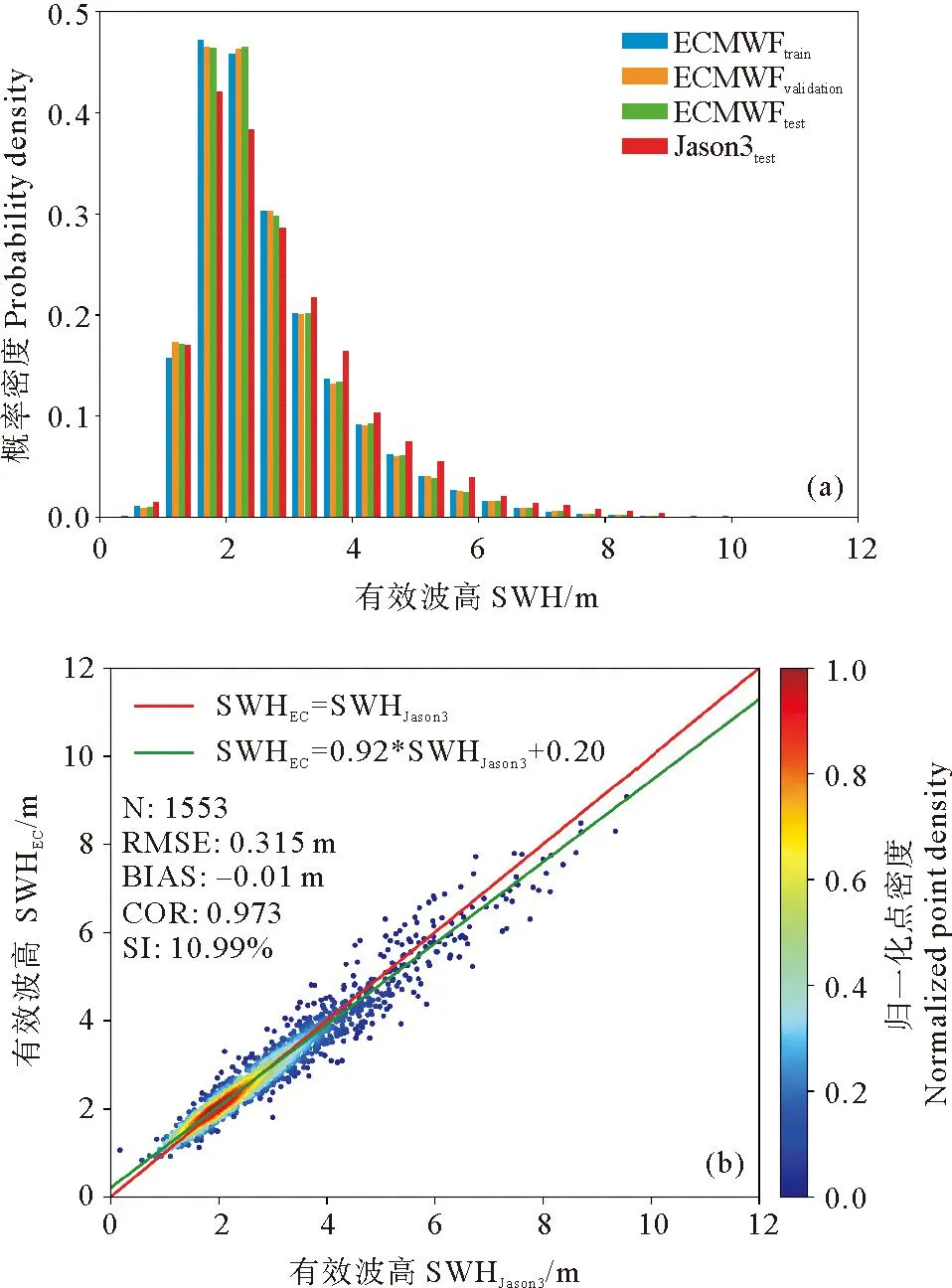
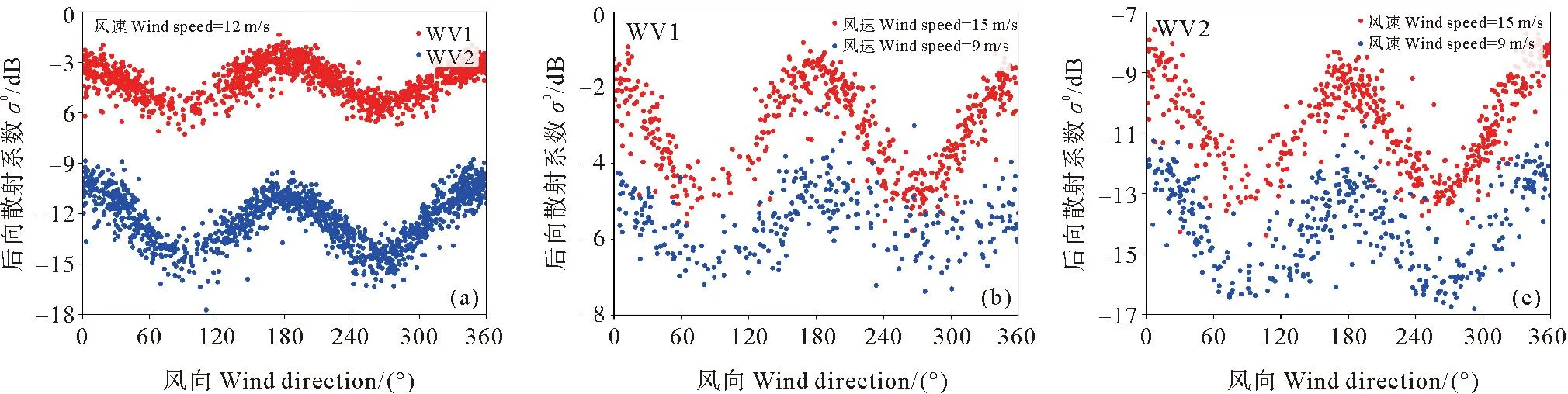
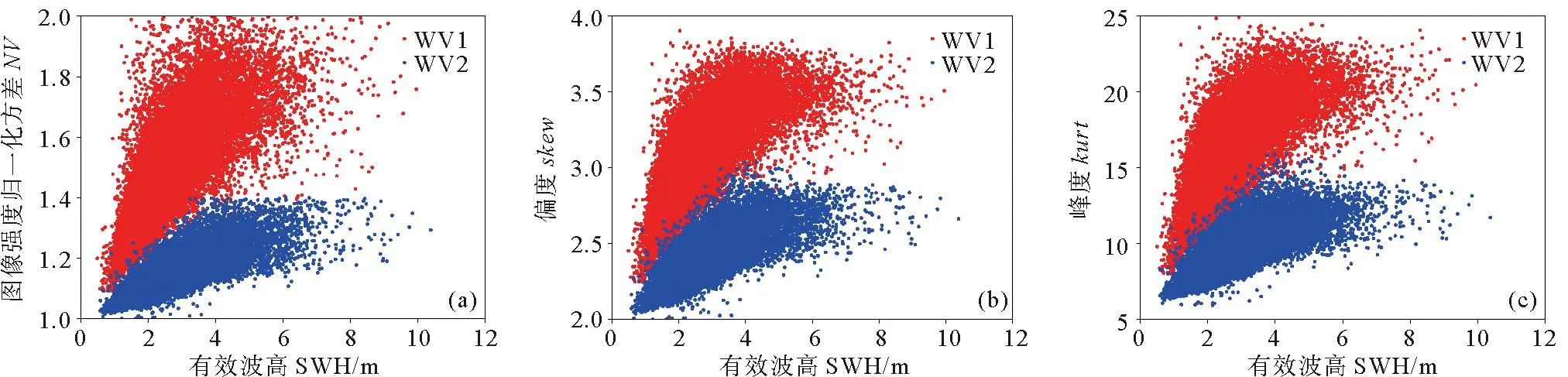
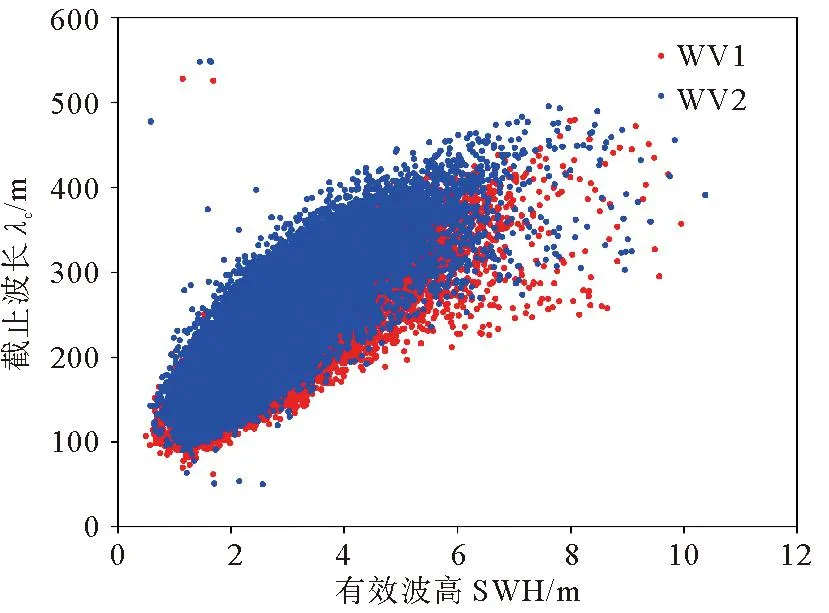
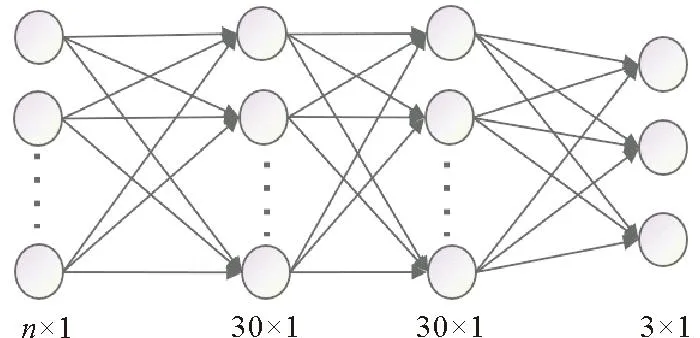
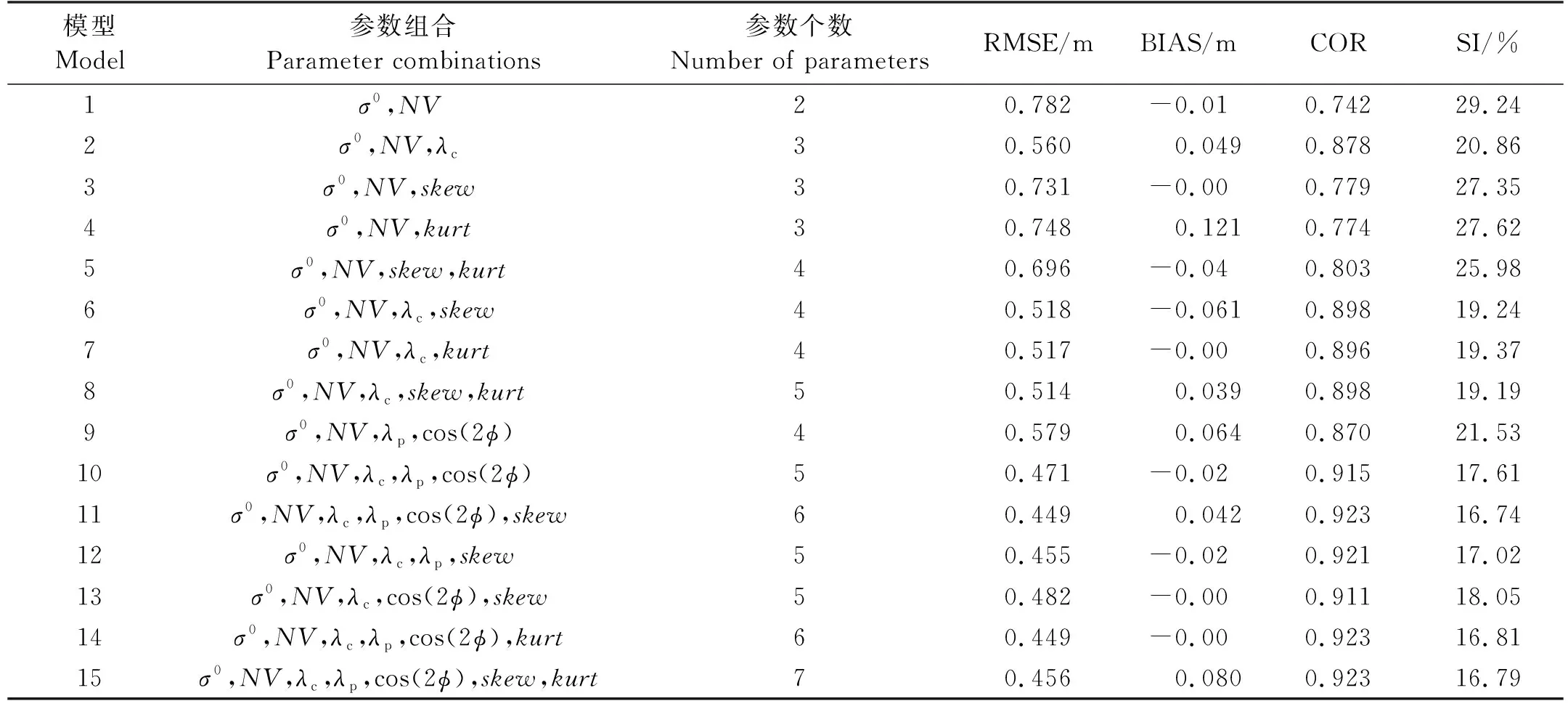
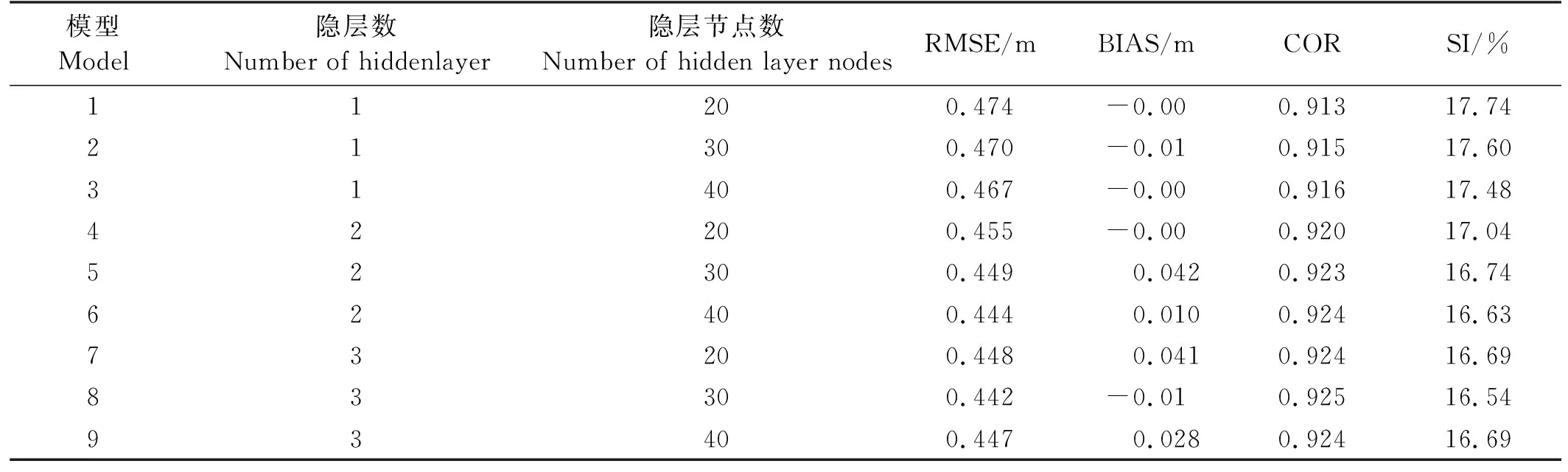
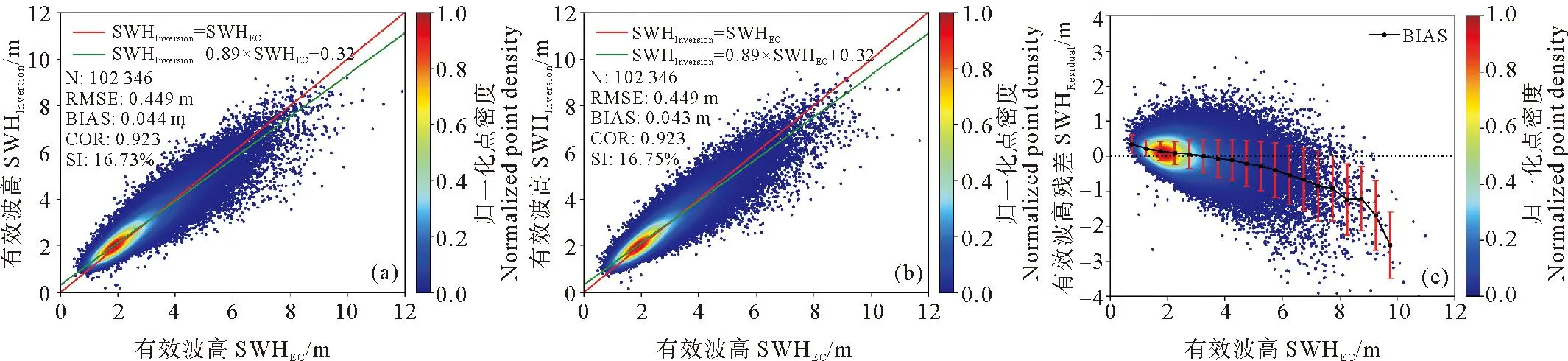
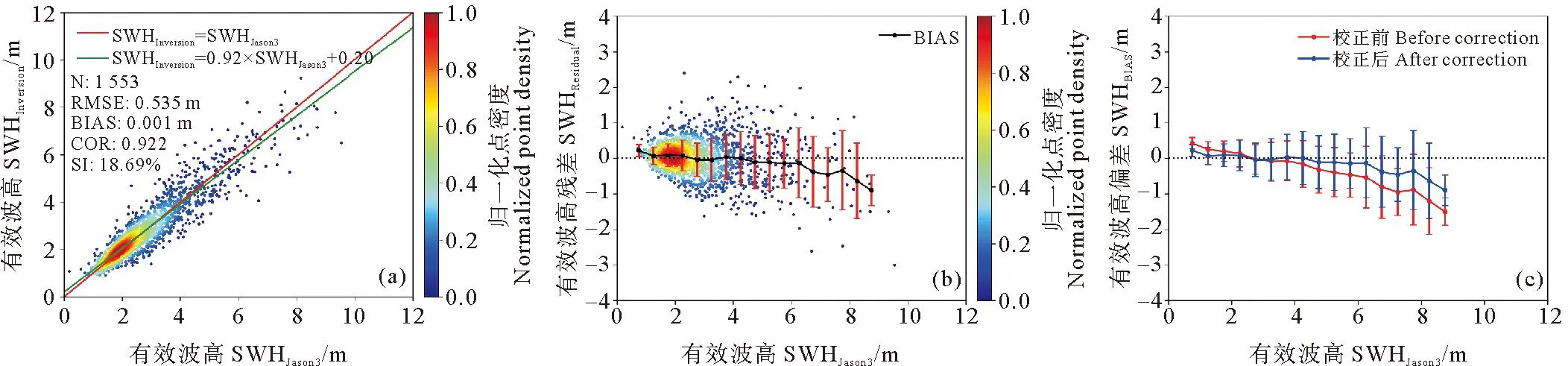
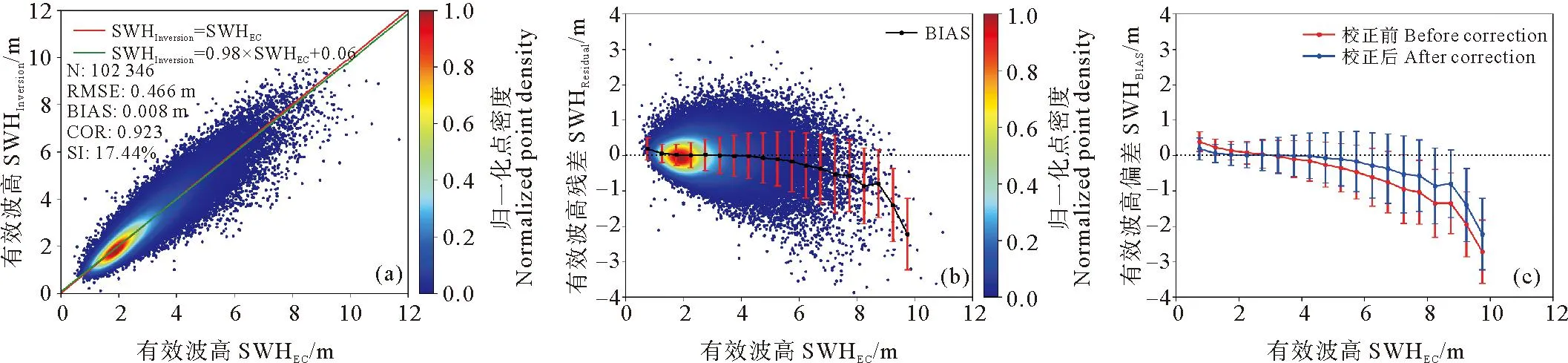
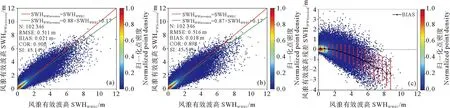
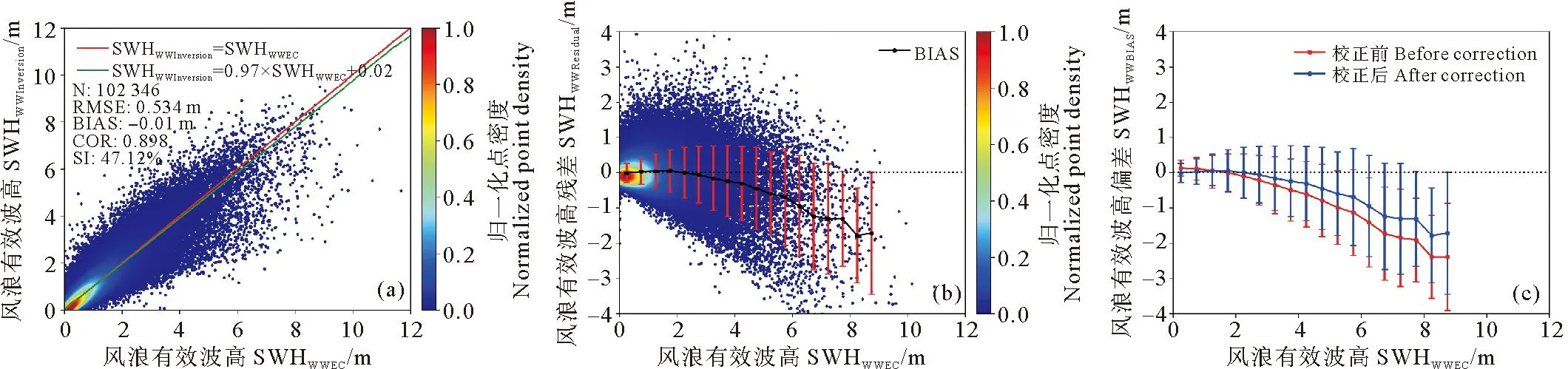
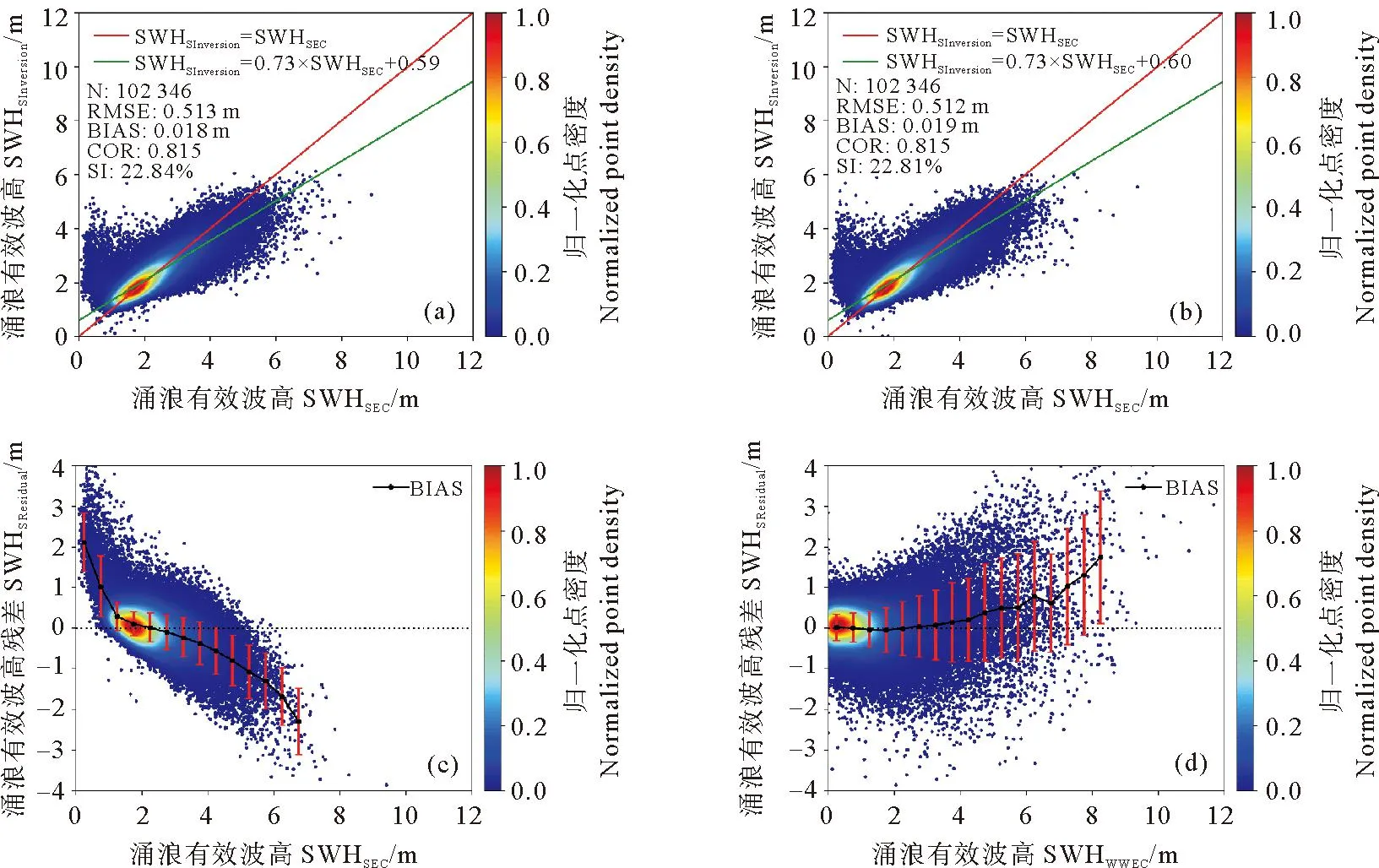
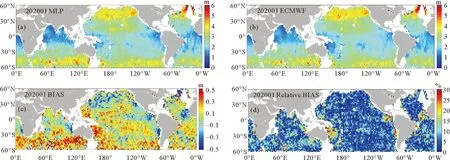
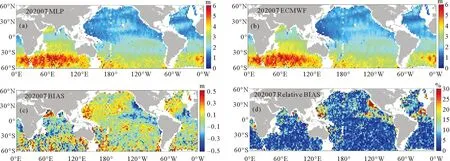
式中:I表示SAR图像上每个像素点的强度;〈I〉表示SAR图像的强度平均值。随着雷达入射角度的增大,SAR图像的信噪比降低,设置不同的阈值可以保证两个入射角度的SAR图像质量基本一致。对于WV1数据,取1

ECMWF数据是将预报数据与全球观测得到的气象数据相结合,形成的一个完整的气象数据集。可以提供全球的海表风场信息和海浪信息。文中用到的海浪信息包括整体海浪有效波高、风浪有效波高和涌浪有效波高。时间分辨率为1 h,空间分辨率为0.5°×0.5°。

Jason3卫星发射于2016年,是Jason2卫星的后续卫星。Jason3卫星保证了海面高度测量数据的连续性,可以为一些预报应用提供数据产品支持。Jason3卫星高度计的Ku波段海浪有效波高数据Jason2卫星高度计测量的海浪有效波高数据具有良好的一致性[35-36],因此在数据匹配时选用Ku波段海浪有效波高数据。

2 海浪有效波高反演方法

2.1 数据匹配

根据SAR图像的观测时间和经纬度信息匹配相应的海浪有效波高信息。SAR图像中心点经纬度与ECMWF数据的经纬度相距小于0.25°,时间间隔小于30 min。这样可以确保海浪信息与SAR数据具有较好的时空一致性。

SAR图像匹配Jason3卫星数据用于验证模型。首先用Jason3数据中提供的地表类型标志、海冰标志和降雨标志筛选数据,在数据匹配时,SAR图像中心点与Jason3数据地理位置相距小于100 km,距离计算公式如公式(2)所示,其中,D为地球上两个经纬度点之间的距离,R为地球半径,约为6 371 km,(lonS,latS)为SAR图像中心点的经纬度,(lonJ,latJ)为Jason3卫星高度计数据点的经纬度。时间间隔小于30 min。

(2)

图1(a)显示海浪有效波高主要分布在1～4 m之间,其余海况的数据量偏少,而且ECMWF三个数据集和Jason3海浪有效波高的统计分布特征具有很好的一致性。图1(b)中给出了ECMWF海浪有效波高与Jason3海浪有效波高数据之间的散点图,二者具有良好的一致性。二者之间的相关系数为0.973,均方根误差为0.315 m,离散指数为10.99%,这说明ECMWF数据是可靠的,可以用于训练MLP模型。

图1 海浪有效波高概率密度分布(a)及ECMWF和Jason3有效波高数据(b)

2.2 参数选取

2.2.1 后向散射系数(σ0) SAR复数据经过辐射定标后可以得到σ0,当风速小于20m/s时,σ0与雷达入射角、风速和风向有强相关性(见图2)。σ0常被用来反演海表面风场和风浪信息。目前基于σ0的海表面风场反演技术已经日臻成熟,并进行业务化应用。对于C波段VV极化SAR数据,反演风速的地球物理模式函数成为CMOD模型,常用的模型包括CMOD4、CMOD-IFR2、CMOD5、CMOD5.N、CSARMOD和CMODH。σ0的大小与风浪有效波高之间也存在直接关系,因此在本文中将σ0视为反演海浪有效波高重要的训练参数之一。由图2可见,σ0的大小与入射角和风向也具有强相关性。然而在SAR图像中难以提取风向,而且WV1和WV2数据的入射角度近似为两个常数值,因此,风向和入射角度并未选取为输入参数。

图2 σ0与雷达入射角的关系(a),WV1数据σ0与风速、风向的关系(b)及WV2数据σ0与风速、风向的关系(c)

2.2.2 图像强度归一化方差(NV)、偏度(skew)和峰度(kurt)NV表征了SAR图像的均质性,反映了SAR图像中海浪对回波强度的调制影响,通常而言,在线性波理论下,海浪的有效波高越大,SAR图像所受到的流体力学调制、倾斜调制以及速度聚束调制影响越显著,导致NV值越大,因此,如图3(a)所示NV值与海浪有效波高之间存在显著相关性。随着海浪有效波高的增大,SAR图像中的速度聚束调制会引起强烈的非线性效应,此时NV值与海浪有效波高之间的相关性不明显。由于倾斜调制效应以及回波的信噪比特征与入射角度有关,因此如图3(a)所示,入射角度不同时海面SAR图像的NV值存在明显差异。skew和kurt用于表示SAR图像的三阶和四阶统计量,反映了SAR图像纹理的非线性特征。图3(b)和(c)中skew和kurt与海浪有效波高的散点图,其表现出的特征与NV类似。公式(3)和(4)给出了skew和kurt计算公式,s是σ0的标准差。本文中NV、skew和kurt也被选择为输入参数。如图3所示,这三个参数均对高海况敏感度降低,这也导致多层感知器模型在高海况下误差增大。

(3)

图3 NV与海浪有效波高的关系(a), skew与海浪有效波高的关系(b)及kurt与海浪有效波高的关系(c)

(4)

(5)

图4 海浪有效波高与截止波长的关系

(6)

2.3 模型描述

经典感知器模型一般包括一个输入层,一个隐层和一个输出层,每层的节点个数可以根据需要进行调整。该模型的优点是结构简单,模型参数少,收敛速度快。本文使用多层感知器模型反演海浪有效波高信息,将2.2小节中与海浪有效波高相关的参数作为模型的输入,模型的输入节点个数根据输入参数的组合进行调整。隐层的层数和节点个数反映了模型提取信息的能力。隐层参数过少,不能充分提取海浪信息;参数过多,容易导致过拟合。经过多次试验,当模型中设置两个隐层,每个隐层设置30个节点时,模型的反演结果最优。最优的模型结构如图5所示,模型的输出是海浪有效波高信息。

图5 MLP模型

在模型的训练过程中,本文设置模型的初始学习率为0.01,并对学习率进行动态调整。每次训练完毕后学习率衰减为原来的95%,随着训练次数的增加,学习率降低,模型参数调整幅度变得缓慢,更有利于模型收敛。训练数据集中数据量较大,可以分批次进行训练,每个批次数据量设置为128。在训练次数相同的情况下,分批次训练可以使模型参数调整次数更多,节约模型训练时间。由于模型的输出是海浪有效波高信息,我们选择ReLu函数作为激活函数,ReLu函数的表达式如公式(7)所示。相比于其他的激活函数,ReLu函数运算效率更高,而且没有饱和区,不会导致梯度消失问题。为了衡量模型输出结果的准确性,我们选择均方误差函数作为损失函数,如公式(8)所示。

(7)

(8)

最后使用测试集验证模型的可用性。选用均方根误差(RMSE)、平均偏差(BIAS)、相关系数(COR)和离散指数(SI)四个参数分析海浪有效波高的反演精度,各参数的具体表达式如下:

(9)

(10)

(11)

(12)

式中:y*是反演结果;y是真值结果。

3 反演结果分析

本文在这一节中分析了单输出感知器模型和多输出感知器模型对海浪有效波高信息的反演情况。单输出感知器模型仅仅输出整体海浪有效波高,多输出感知器模型输出整体海浪有效波高、风浪有效波高和涌浪有效波高。最后分析了校正函数对由于数据分布不均衡和SAR参数饱和导致的模型系统偏差的校正效果。

3.1 单输出模型

在单输出感知器模型的训练过程中,以σ0和NV为基础输入,然后逐渐增加输入参数,提高整体海浪有效波高的反演精度,并筛选出最有效和最精简的输入参数组合。表1给出了不同输入参数组合时的整体海浪有效波高反演结果。

表1 单输出模型整体海浪有效波高反演结果

表2 不同入射角度整体海浪有效波高反演结果

表1中均方根误差、平均偏差、相关系数和离散指数四个参数的大小反映出不同输入参数组合所对应的海浪有效波高反演精度,在研究过程中,通过逐个增加输入参数,从而对比分析每个输入参数对反演精度的影响。

(1)对比输入组合1和2可以发现,加入λc后,均方根误差下降0.222 m,散射指数下降8.38%,相关系数提高0.136,有效波高的反演精度有明显提高。在其他参数组合中加入截止波长后,也可以看到反演精度的提高。截止波长对于反演整体海浪有效波高有明显地积极作用,这与其他研究人员的结论是一致的。

(2)对比输入组合1、3、4和5可以发现,参数组合中加入skew或kurt也能提高整体海浪有效波高反演精度。同时加入两个参数,精度提高更加明显。对比组合10、11、14和15可以发现,随着模型中输入参数的增多,skew或kurt对于提高反演精度作用一致,同时加入这两个参数,反演精度降低。本文在最终的输入参数中只保留skew,可以减少特征参数冗余,加快模型的收敛速度。

(3)对比输入参数组合1和9可以发现,输入参数中加入λp和φ后,有效波高的反演精度明显提高。均方根误差下降0.203 m,散射指数下降7.71%,相关系数提高0.129。对比输入组合11、12和13可以发现λp作用更加明显。

(4)通过15个输入参数组合对比,组合11在测试数据集中表现最优,其均方根误差为0.449 m,相关系数为0.923,散射指数为16.74%。

对于输入参数组合11,入射角度约为23°的WV1数据和入射角度约为36°的WV2数据的海浪有效波高反演结果如表格2所示。可以发现,入射角度对海浪有效波高反演精度影响不大,均方根误差约为0.45 m,相关系数约为0.92,离散指数约为16.7%。

上面分析了不同输入参数组合和雷达入射角度对整体海浪有效波高反演精度的影响。接下来通过改变模型的隐层层数和节点个数来分析的模型结构对反演结果的影响。表3给出了隐形层数和节点数不同时的海浪有效波高反演结果。增加模型的隐层数和隐层节点数一定程度上可以提高反演精度。但是,过多的隐层和隐层节点对提高反演精度的作用不再明显,而且不利于模型收敛,模型训练时间也会增加。在本文中,我们最终选择表3中的模型5作为最优反演模型,即模型中包含两个隐层,每个隐层包含30个节点。

表3 模型结构对整体海浪有效波高反演结果的影响

为了更加直观地分析模型反演结果,图6(a)和(b)中给出了模型反演结果与ECMWF有效波高数据之间的散点图。从图6(a)和(b)可以发现验证集和测试集的反演结果相近。两个数据集的均方根误差均为0.449 m,相关系数为0.923,散射指数约为16.7%。图6(c)显示绝大部分数据点残差小于1 m,反演结果较好。当海浪有效波高较大时,模型输出结果偏小,这主要是由于两个原因导致的,其一,训练数据集中数据分布不均匀,高海况SAR数据较少;其二,高海况时输入参数会出现饱和特征。为了一定程度上解决高海况时整体海浪有效波高的模型反演结果偏小这一问题,本文根据验证数据集的最小二乘法拟合结果构建校正函数,从而对模型反演结果进行二次校正。公式(13)则给出了校正函数表达式。

((a)验证集反演结果;(b)测试集反演结果,绿色实线是最小二乘法拟合结果;(c)测试集残差(SWHInversion-SWHEC),将有效波高按照0.5 m的间隔划分区间,并对区间内的残差求均值和标准差可得误差拟合曲线和误差棒。(a) The inversion results of validation data set;(b) The inversion results of test data set, The green line is the result of the least squares fit; (c) The residuals of test set(SWHInversion-SWHEC), The SWH is divided into intervals at 0.5m interval and finding the mean and standard deviation of the residuals within the interval yields an error fitting curve and error bars.)

SWH=(SWHinversion-0.32)/0.89。

(13)

图7给出了二次校正后的反演结果。从图7(b)和(c)可以发现,高海况时校正函数对模型反演结果有一定修正,从而扩大了MLP模型的适用范围。为了进一步验证MLP模型和校正函数的有效性,图8中基于Jason3高度计海浪有效波高数据对该方法进行了检验。如图8所示,该方法反演结果与Jason3高度计海浪有效波高数据之间的均方根误差为0.535 m,相关系数为0.922,散射指数为18.69%。由图8(c)中的偏差曲线对比可见校正函数的有效性。

((a)有效波高反演结果; (b)有效波高残差(SWHInversion-SWHEC);(c)校正前后的有效波高偏差曲线。(a) The inversion results of SWH; (b) The residuals of SWH(SWHInversion-SWHEC); (c) The bias line of SWH before and after correction.)

((a)有效波高反演结果;(b)有效波高残差(SWHInversion-SWHJason3);(c)校正前后的偏差曲线。(a) The inversion results of SWH; (b) The residuals of SWH(SWHInversion-SWHJason3); (c) The bias line of SWH before and after correction.)

3.2 多输出模型

海浪包括风浪和涌浪,整体海浪有效波高也可以用风浪有效波高与涌浪有效波高进行表示。公式(14)中SWH为海浪有效波高,SWHWW为风浪有效波高,SWHS为涌浪有效波高。

(14)

单输出模型仅仅反演整体海浪有效波高,无法区分风浪和涌浪有效波高。为了进一步探究多层感知器模型在反演海浪有效波高时的误差来源,在最优模型结构的基础上,使模型的输出层由原来的一个节点增加为三个节点,即模型能够同时输出整体海浪有效波高、风浪有效波高和涌浪有效波高。

图9是多输出模型反演的整体海浪效波高结果。由图9可见,多输出模型和单输出模型对整体海浪有效波高的反演结果相似。公式(15)则给出了针对该结果的校正函数,对比公式(13)和公式(15),两个公式差异很小。图10是基于公式(15)二次校正后的整体海浪有效波高结果。图11是二次校正后的多输出模型反演结果与Jason3高度计海浪有效波高数据的比较。由图9、图10和图11中的结果可见,多输出模型可以有效反演整体海浪有效波高 。

图9 验证集有效波高反演结果(a),测试集有效波高反演结果(b)及测试集有效波高残差(SWHInversion-SWHEC)(c)

((a)有效波高反演结果; (b)有效波高残差(SWHInversion-SWHEC);(c)校正前后的有效波高偏差曲线。(a) The inversion results of SWH; (b) The residuals of SWH(SWHInversion-SWHEC); (c) The bias line of SWH before and after correction.)

((a)有效波高反演结果;(b)有效波高残差(SWHInversion-SWHJason3); (c)校正前后的偏差曲线。(a) The inversion results of SWH; (b) The residuals of SWH(SWHInversion-SWHJason3); (c) The bias line of SWH before and after correction.)

SWH=(SWHInversion-0.34)/0.88。

(15)

多输出模型能够同时输出风浪和涌浪的有效波高。图12是风浪有效波高的反演结果,测试集的均方根误差为0.516 m,相关系数为0.898,散射指数为45.54%。图12(c)表明风浪较大时MLP模型输出的风浪有效波高偏小,这也是整体海浪有效波高反演误差的来源之一。同样,我们针对风浪有效波高反演结果构建校正函数(16),通过图(13)中经过校正函数二次校正的数据可见,风浪较大时,校正后的反演结果有所改善,图13(c)的偏差曲线的变化也说明了这一点。

((a)验证集反演结果; (b)测试集反演结果; (c)测试集残差(SWHWWInversion-SWHWWEC)。(a) The inversion results of validation data set; (b) The inversion results of test data set; (c) The residuals of testset(SWHWWInversion-SWHWWEC).)

SWHWW=(SWHWWInversion-0.17)/0.88。

(16)

多输出模型的涌浪有效波高反演结果如图14所示,测试集涌浪有效波高的均方根误差为0.512 m,相关系数为0.815 m,散射指数为22.81%。图14(c)中的残差表明涌浪有效波高较小时,模型反演结果远大于ECMWF涌浪有效波高,导致该现象的主要原因可能是:涌浪有效波高较低时,涌浪对输入参数的调制作用消失,此时,输入参数仅能反映风浪特征,而不能够体现涌浪特征,从而导致当涌浪有效波高较小时,模型反演误差较大。涌浪有效波高较大时,与前面的反演结果类似,模型反演结果小于ECMWF提供涌浪有效波高。图14(d)显示了涌浪有效波高反演残差与风浪有效波高的关系,风浪有效波高越大,涌浪有效波高反演残差越大。由图14可见:多输出MLP模型的涌浪有效波高反演误差主要集中于涌浪有效波高较低和涌浪有效波高较高处,构建校正函数对改善模型反演结果并不明显,因此在本文中并未针对涌浪的模型反演结果构建校正函数,这也是后面的研究中需要改进的地方。

((a)风浪有效波高反演结果; (b)风浪有效波高残差(SWHWWInversion-SWHWWEC);(c)校正前后的风浪有效波高偏差曲线。(a) The inversion results of SWHWW; (b) The residuals of SWHWW (SWHWWInversion-SWHWWEC); (c) The bias line of SWHWW before and after correction.)

((a)验证集反演结果; (b)测试集反演结果; (c)测试集残差(SWHSInversion-SWHSEC); (d)测试集残差与风浪有效波高的关系。(a)The inversion results of validation data set; (b)The inversion results of test data set; (c)The residuals of test set(SWHSInversion-SWHSEC); (d)The relation between the residuals of SWHS and the SWHWW.)

为了分析文中的海浪有效波高反演方法在全球海域适用性,选取2020年1月和7月SAR数据对全球海域进行整体海浪有效波高反演并绘制月平均图,在图15和图16中将文中方法的反演结果与ECMWF数据进行比较。并利用公式(17)和(18)计算偏差和相对偏差。由图15和16可见:在大部分海域整体海浪有效波高反演结果良好。高海况时偏差较大,一般小于0.5 m;低海况时,相对偏差较大,一般小于30%。

(17)

((a)校正后的模型反演结果;(b)ECMWF数据;(c)月平均偏差;(d)月平均相对偏差。(a)The inversion results of model after correction; (b)ECMWF data; (c)Monthly average bias; (d)Monthly average relative bias.)

((a)校正后的模型反演结果;(b)ECMWF数据;(c)月平均偏差;(d)月平均相对偏差。(a)The inversion results of model after correction; (b)ECMWF data; (c)Monthly average bias; (d)Monthly average relative bias.)

(18)

4 结论

本文提出将MLP模型和校正函数相结合的方法反演整体海浪有效波高、风浪有效波高和涌浪有效波高。首先利用模型反演海浪有效波高信息,然后根据验证数据集的反演结果构建校正函数,并在测试数据集上验证校正函数的有效性。最后用高度计数据证明了该方法的有效性。通过本文研究得到的主要结论如下:

(1)后向散射系数、图像强度归一化方差、截止波长、主波波长、主波波向和图像偏度参数与海浪有效波高具有强相关性,将这些参数作为MLP模型的输入反演海浪有效波高信息效果良好。

(2)通过分析MLP模型中隐层层数和隐层结点数对反演结果的影响,我们认为MLP模型中包含两个隐层,每个隐层有30个节点时效果最优。

(3)论文中建立了单输出MLP模型反演整体海浪有效波高和多输出MLP模型反演整体海浪有效波高、风浪有效波高和涌浪有效波高。对于整体海浪有效波高而言,单输出模型和多输出模型的反演结果是一致的。由于训练数据集中高海况数据较少和高海况下SAR参数的饱和现象,导致在高海况时模型反演结果偏低。

(4)将多输出模型反演的风浪有效波高和涌浪有效波高与ECMWF预报数据相比,风浪有效波高较高时,模型反演的风浪有效波高也出现偏低现象;当涌浪有效波高较低或较高时,模型反演的涌浪有效波高均出现较大误差。

(5) 文中根据验证数据集的模型反演结果与ECMWF预报数据之间的偏差,构建了针对整体海浪有效波高和风浪有效波高的校正函数,利用校正函数对模型反演结果进行二次校正,可以减小高海况下模型的反演误差。对于涌浪有效波高的模型反演结果而言,无法构建有效的校正函数以减小误差,这也是在后续研究中需要进一步改进的地方。