采用多元非线性回归模型的无头铆钉安装干涉量预测
2024-01-16李晓锋常正平高雅芝霍永兴宋建生王仲奇
李晓锋,常正平,高雅芝,霍永兴,宋建生,王仲奇
(1. 西北工业大学机电学院,710072,西安; 2. 中航西安飞机工业集团股份有限公司,710089,西安)
无头铆钉是目前飞机壁板自动钻铆装配中采用的主要铆钉类型,具有质量小、结构简单等特点,可形成较均匀分布的干涉量,成倍地提高了连接结构的疲劳寿命,同时具有良好的密封效果,故广泛应用于Y-20、C919、ARJ21等飞机装配中[1-2]。干涉量是评价无头铆钉安装质量的关键指标[3],干涉量太大会导致构件残余应力变大,甚至引发裂纹等损伤,干涉量太小又难以保证其在提高疲劳寿命及密封性方面上的优势,因此开展干涉量分析和预测对提高接头质量及保障可靠性服役至关重要。
在自动钻铆过程中,影响干涉量水平的参数主要有铆接力、铆接过程时间、钉孔配合公差等工艺参数和弹性模量、屈服强度等材料性能参数[4-6]。De Rijck等[3]采用理论分析方法,建立了铆接力与镦头尺寸间的映射关系,并在多种材料下的进行试验验证。Cheraghi等[7]采用有限元仿真分析并结合统计分析方法,研究了铆接力、铆钉尺寸以及钉与孔配合尺寸对铆接质量的影响,发现采用规定的沉头窝深度会导致被连接件间产生间隙,若降低沉头窝深度,在保证铆接质量的情况下可允许更大的钉与孔配合尺寸公差及铆接力范围。刘连喜等[8]模拟分析了无头铆钉铆接变形形式,同时结合正交试验法研究了多种自动钻铆工艺参数对铆接干涉量的影响,发现压铆力是影响铆接干涉量的主要因素。李超等[9]采用BP神经网络对铆接干涉量均匀性及壁板变形程度进行预测,结合多目标粒子群算法对压铆力、夹紧力和压铆过程参数进行优化,并进行了试验验证。李艳等[10]研究了铆钉材料对铆接变形的影响,结果发现采用强度比连接件小的铆钉材料可以减小裂纹等损伤出现的概率。Aman等[11]分析了铆接顺序、铆钉间距及被连接件间隙对铆接质量的影响,确定了最佳工艺参数组合,采用单一变量控制法进行试验设计,得出残余应力和三者之间的函数关系。陈贵坤等[12]分析了板厚、板材硬度和铆钉硬度与自冲铆工艺参数的影响效果,结合等高线图研究了两因素交互作用对冲击载荷等工艺参数的显著性效果。常正平等[13]研究了铆接力、铆钉伸出量、铆接时间、停留时间及夹紧力对铆接变形的影响,表明铆接力是影响铆接变形的最关键的因素。综上,目前开展的研究主要集中在工艺参数对铆接质量的影响,而对被连接件材料性能参数对干涉量的影响研究较少。
为进一步明晰材料性能对干涉量的影响规律且为新材料扩展应用提供可靠性预测,本文采用有限元与正交试验相结合的方法,研究被连接件材料性能参数及其交互作用对无头铆钉安装干涉量的影响,并建立干涉量的多元非线性回归预测模型,为实际铆接试验提供指导。
1 有限元建模
1.1 模型描述
(1)几何模型建立。由于铆接过程的几何模型结构简单且具有对称性,直接在ABAQUS软件中建立模型,结构示意如图1所示,并在分析过程中采用1/4模型以减少运算时间[14]。铆钉选用直径d=4.78 mm、长度h=16 mm的无头铆钉;钉孔直径为D=4.88 mm;上、下被连接件采用厚度t1=t2=3 mm、L/2=15 mm的铝合金板材;铆模选用平铆模。
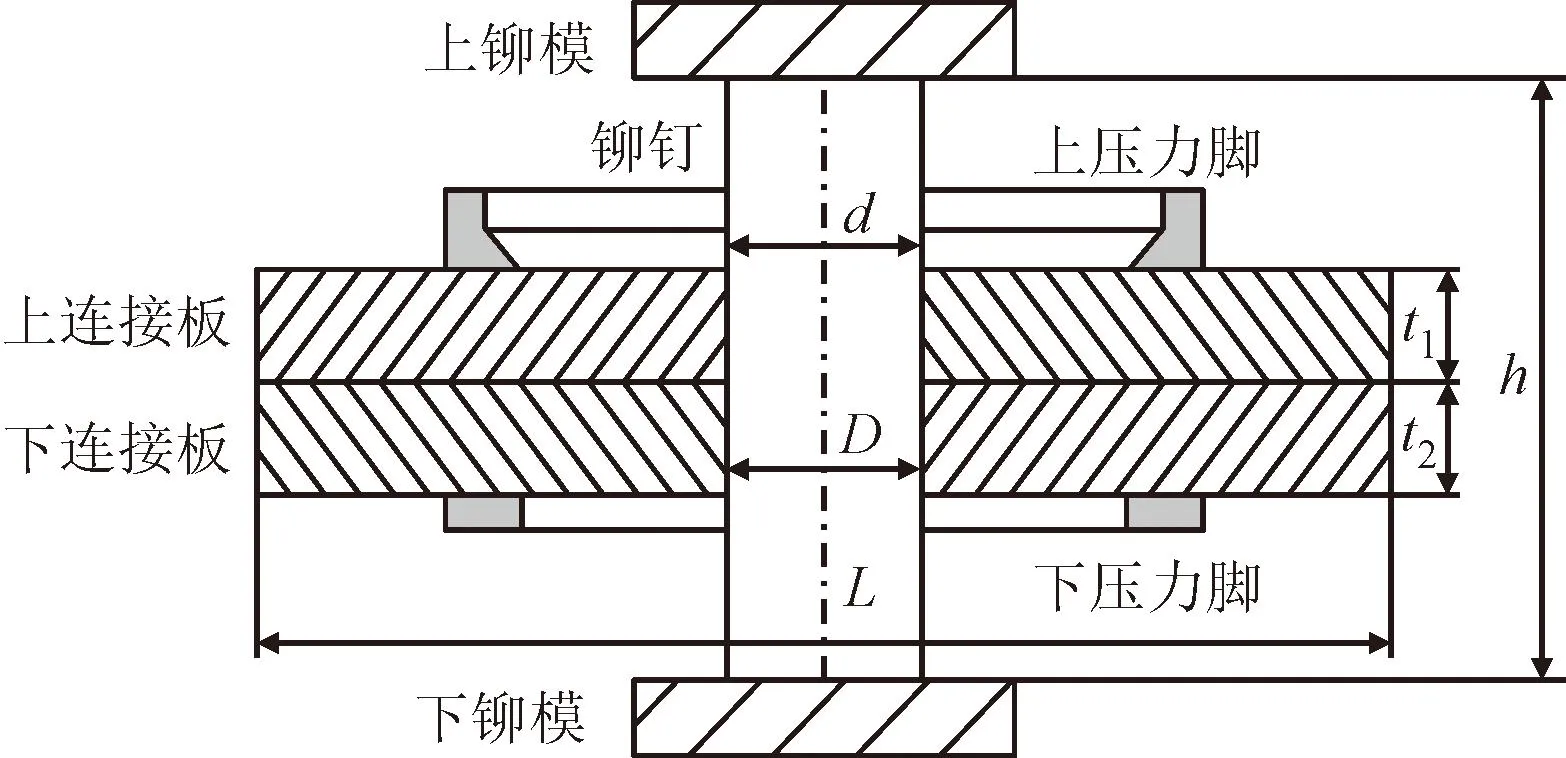
图1 铆接模型示意图Fig.1 Schematic diagram of riveting model
(2)材料属性设定。目前,常用的航空结构件多为2024-T351、7055-T76511等型号铝合金材料[15-17],模型本构关系采用Johnson-Cook模型(应力σ=A+Bεn),暂不考虑应变速率以及温度的影响[18],不同系列铝合金材料密度以及泊松比基本一致。因此,后续主要研究被连接件材料性能参数中弹性模量E、屈服强度A、强化系数B以及应变强度指数n对铆接干涉量的影响,具体材料设定在正交试验部分进行详细描述。铆钉选用2117-T4铝合金材料,铆钉及常用航空结构件材料性能参数见表1。本文中铆钉材料保持一致,故无需进行材料性能参数变换,直接使用试验得出的应力-应变曲线的离散化数据,塑性阶段材料应力-应变曲线见图2。上、下铆模刚度相较于铆接及被连接件大很多,为简化计算,设定为刚体。

表1 常用航空结构件及铆钉材料性能参数
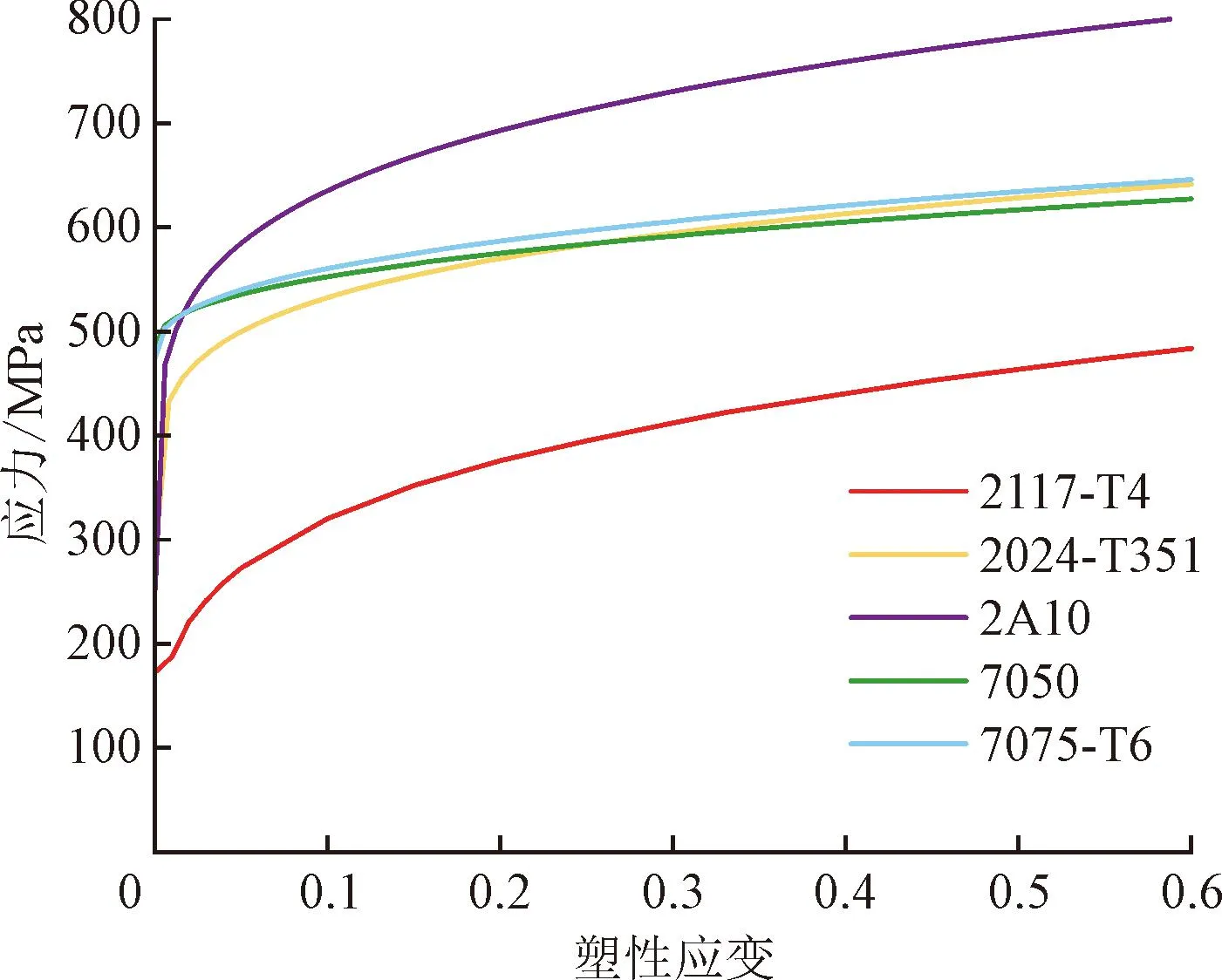
图2 各材料的应力-应变曲线Fig.2 Stress-strain curves of materials
(3)网格划分。网格采用C3D8R六面体单元,实行减缩积分,但会导致单元刚度矩阵求解不完全,易出现刚度为零的情况,丧失抵抗变形的能力并使得模型计算发散。为解决上述问题,设置默认的沙漏控制,添加相应的沙漏阻尼,即设定线性体积黏性参数为0.06,二次体积黏性参数为1.2。为提高运算效率的同时保证运算精度,仅在孔周变形较大处进行网格加密[19],如图3所示。

图3 网格划分及边界条件设置Fig.3 Mesh division and setting of boundary conditions
(4)接触及摩擦处理。根据各部件表面主从关系设置接触,切向行为采用“罚”接触,摩擦系数为0.2[20-21],法向行为采用“硬”接触方式。
(5)载荷及边界条件确定。限制被连接件右端面沿X向移动以及后端面沿Z向移动;固定上压力脚,限制下压力脚除沿Y向移动以外的自由度,并在下压力脚的下表面施加压强载荷;限制铆模除沿Y向移动以外的自由度,铆接力施加在与铆模相关联的参考点见图3。
1.2 有限元模型验证
为验证铆接过程有限元模型的模拟效果,选用被连接件材料为2024-T351和7055-T76511分别进行无头铆钉自动钻铆试验和仿真分析,每种材料设置3次重复试验,其中一组试验及对应仿真分析结果如图4所示,图中数据代表在相应干涉量测量位置铆钉直径的试验数据和仿真数据。在实际自动钻铆过程中,试件采用的铆接力为38.4 kN,压紧力为19.64 MPa,锪窝端的镦头在铆接完成后会被铣平以保证飞机外形的平整性,因此铆接试验中镦头同样被铣平。根据《航空制造工程手册》[22]干涉量测量要求以及主机厂实际操作规范,干涉量测量部位如图5所示,分别用G1、G2、G3和G4表示。采用光学显微镜及相应配套测量软件Imageview按照待测位置测量铆接试验干涉量,并与仿真模拟值进行对比分析,分析结果如表2所示。其中,在测量前要先进行尺寸标定以确保测量精度,并将小数点后万分位作为估读位,结果对比中实验数据为3次重复试验的均值。
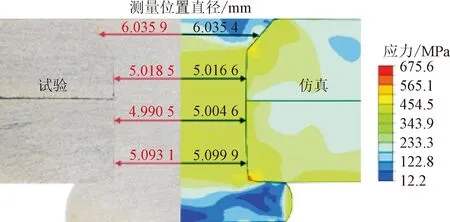
(a)2024-T351
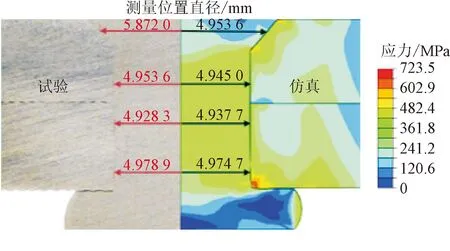
(b)7075-T76511

图5 干涉量测量位置示意图Fig.5 Diagram of interferometric measurement position
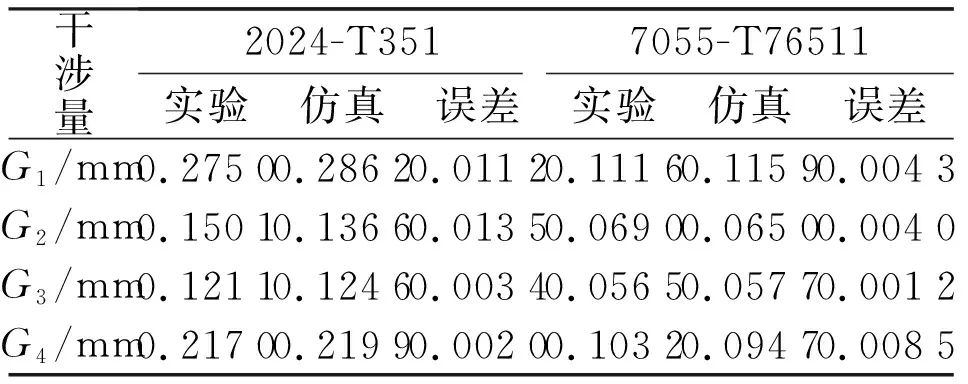
表2 仿真与试验结果对比
从表2中可以得出,无头铆钉铆接过程仿真结果与试验数据在G1、G2、G3、G4的误差均在10%以内,且最大误差为0.014 mm,在工程应用接受范围内,因此建立的有限元模型可用于铆接过程模拟,可作为后续研究被连接件材料性能对干涉量影响的基础模型。
2 正交试验设计
采用有限元正交模拟方法,研究材料性能参数中弹性模量E、屈服强度A、强化系数B、应变强度指数n对4个测量位置干涉量的影响。通过本文选用的Johnson-Cook本构可以看出,E、A、B、n之间存在耦合作用,因此除了考虑4个因素的独立影响外,还需考虑两因素间的交互作用,用E×A、E×B、E×n、A×n、A×B以及B×n形式表示。
由于受到标准正交表及其相应交互作用表的限制,同时又为了确保所选水平数能够真实反映各因素对铆接干涉量的影响,本文采用五水平-无交互作用及两水平-有交互作用两种正交试验设计方案,探究各因素及其交互作用对干涉量的影响程度。
2.1 无交互作用的正交试验
2.1.1 试验方案设计
根据相关文献以及材料实际应用场景,确定铝合金材料性能参数范围,选取E、A、B和n四因素五水平数据值,选用L25(56) 标准正交表进行正交试验,试验方案如表3所示。
2.1.2 无交互作用正交试验结果分析
按照设计的正交试验方案进行有限元分析,仿真结果见表3所示。可以看出,靠近镦头的位置(G1和G4)干涉量相较于其他的两处位置(G2和G3)更大。这是由于在无头铆钉铆接过程中,上、下端伸出的钉杆部分先被镦粗,造成膨胀处与钉孔发生接触,严重阻碍了铆钉材料向中间流动,因此在镦头附近会更易得到较大的干涉量。
采用Minitab软件对以上数据结果进行极差分析,确定各材料参数对G1、G2、G3和G4影响程度的相对大小。五水平-无交互作用正交试验的极差R分析结果如表4所示。由表4中可以看出,针对G1、G2、G3和G4待测干涉量,屈服强度A的极差值均为最大值,弹性模量E的极差值均为最小值,表明屈服强度对无头铆钉安装干涉量的影响最大,弹性模量的影响最小。各因素间按影响从大到小的主次顺序为屈服强度、应变强度指数、强化系数、弹性模量。

表3 五水平-无交互作用正交试验方案及仿真结果

表4 无交互作用正交试验极差分析
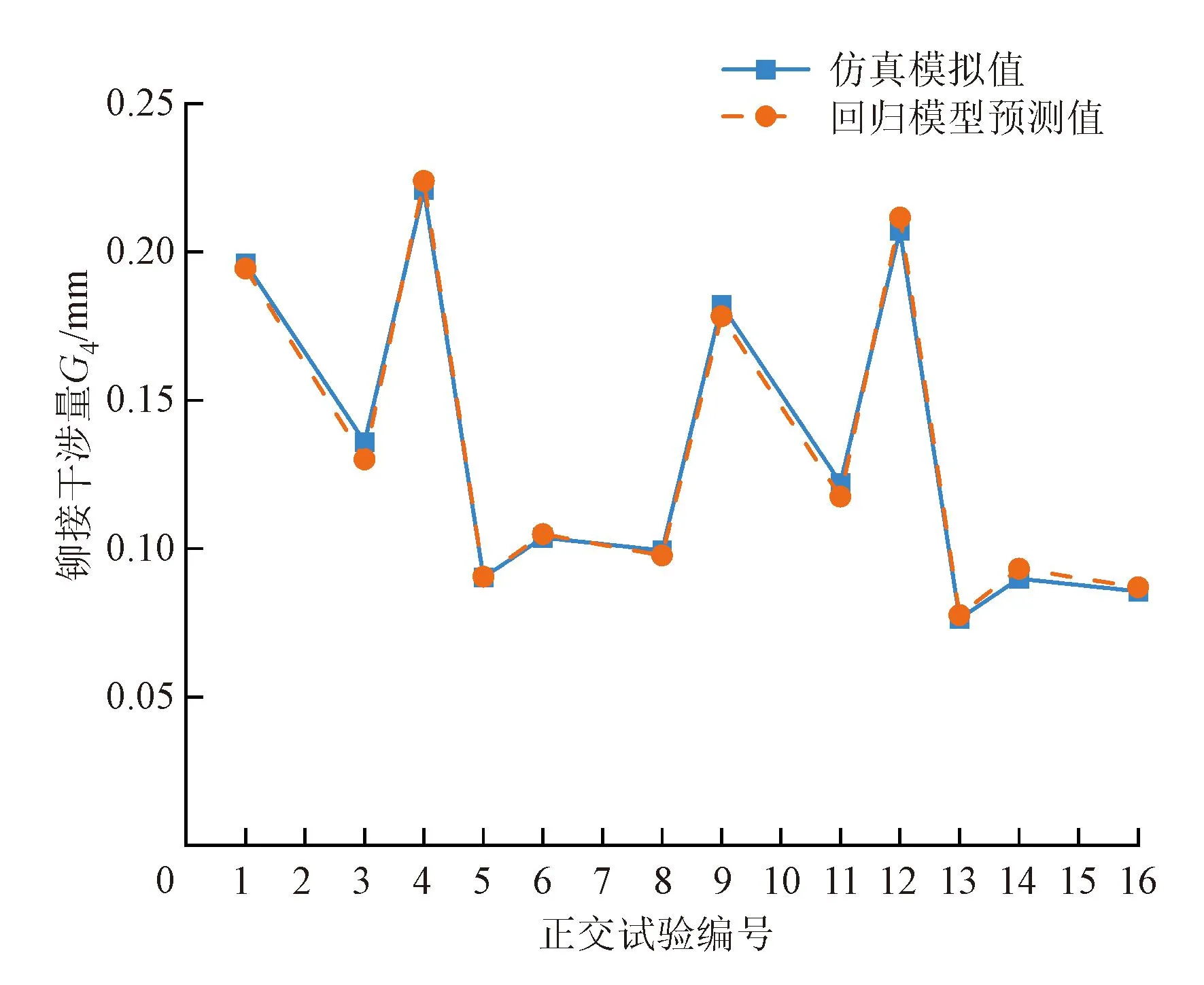
根据无交互作用正交试验极差分析结果,各因素对所有待测位置干涉量的影响效果主次顺序是一致的。为了更加清晰、直观地表达各因素对整体干涉量的影响效果,将平均干涉量作为各因素对干涉量影响效果图的纵坐标,其中平均干涉量表示为某一水平条件下G1、G2、G3和G4的均值。图6中各因素与整体干涉量影响效果曲线的斜率表示该因素对无头铆钉安装干涉量的影响程度,斜率越大,影响越大。从图6可以明显看出,屈服强度A对铆接干涉量的影响最大,应变强度指数n次之,弹性模量E和强化系数B的影响程度相近。其中,应变强度指数n跟铆接干涉量呈正相关,而屈服强度A跟铆接干涉量呈负相关。原因在于,铆接过程中,无头铆钉受力膨胀对钉孔形成挤压,而干涉量的形成主要依靠材料的塑性变形。当铆钉受到一定铆接力时,被连接件屈服强度决定其产生屈服变形的难易程度,屈服强度越大,产生屈服变形越难,导致干涉量变小。根据Johnson-Cook本构和指数函数相关性质,当0 图6 各因素对干涉量的影响效果Fig.6 The effect of factors on the riveting interference 2.2.1 试验方案设计 在2.1节的基础上,综合考虑因素间的交互作用对铆接干涉量的影响,试验方案遵循存在交互作用的正交表选用原则进行设计,即正交表总自由度大于等于各独立因素自由度和交互作用项自由度之和,公式如下 fZ≥fC+fD+fE+…+fC×D+… (1) fZ=N-1 (2) fC=fD=fE=M-1 (3) fC×D=fC×fD (4) 式中:fZ为正交表总自由度;fC、fD、fE为各因素自由度,fC×D表示因素C和因素D的交互作用自由度。N为正交试验方案总试验数;M为各因素水平数。 由于受到标准正交表及相应交互作用表的限制,无法得到四因素五水平(含交互作用项)的标准正交表,因此本小节4个因素均选用两水平,同时为消除各因素水平取值对后续分析结果的干扰,选用2.1节中各因素水平的最大值和最小值作为试验的水平数据。 参照式 (1)~(4),本次考虑交互作用的正交试验E、A、B、n4个因素的自由度均为1,交互作用项E×A、E×B、E×n、A×B、A×n、B×n的自由度均为1。因此,选择L16(215) 正交表进行正交试验设计,同时根据交互作用表[23]确定各相互作用列在正交表中的位置,最终确定的正交试验方案如表5所示。其中,交互作用项并不作为仿真试验输入变量,只用于进行后续数据分析。 表5 二水平-有交互作用的正交试验方案及仿真结果 2.2.2 交互正交试验方差分析 为了提高分析效率,避免重复计算,在五水平-无交互作用正交实验中采用了简单方便的极差分析方法来获取各因素影响效果。对考虑交互作用的正交试验仿真结果选用方差分析方法实现更加精确地定量分析,不仅可以验证极差分析结果的有效性,而且能进一步提高本文两次正交实验分析结果的可靠性,为后续建立干涉量预测模型奠定理论基础。考虑交互作用的正交实验方差分析结果如表6所示。可以看出,针对所有的待测位置,屈服强度A与应变强度指数n的交互作用A×n对铆接干涉量的影响最大,A×B次之,其余4个交互作用因子对干涉量基本没有影响。其中,交互作用A×n对G1的影响略小于单因素B,而对于G2、G3和G4的影响均大于单因素B,同时屈服强度A与强化系数B的交互作用A×B对G1、G2、G3和G4的影响大于单因素E,表明在无头铆接安装过程中各材料参数间的交互作用不能被忽略。 由显著性分析可知,A、B、n、A×n、A×B对铆接干涉量的影响都表现为高度显著性,E对G1的影响表现为显著,对G2、G3和G4表现为高度显著,而其余4个交互作用因子E×n、E×A、B×n和E×B的影响作用均不显著,在后续预测模型建立中将不考虑其对干涉量的影响。因此,综合上述分析可以得到主要的干涉量影响因素从大到小的顺序为A、n、A×n、B、A×B、E,单因素间的主次顺序与无交互作用的极差分析结果一致。 表6 考虑交互作用的正交试验方差分析结果(P=0.05) 多元非线性回归预测模型是通过样本数据进行非线性函数拟合,再采用拟合函数来达到预测响应值的目的,常用的函数形式有幂函数、指数函数、对数函数等。由于幂函数具有较强的泛化能力[12,24-25],本研究选用其作为预测模型的函数形式,基本形式如下 (5) 根据正交试验分析结果可知,A与B对干涉量的影响较大呈负相关,n呈正相关,故A与B处于最小值,n处于最大值时。此时该组合处于极限位置状态,会导致干涉量急剧增大,与其余大多数参数组合结果相差较大,反之亦然。在实际的工程应用当中,不存在铝合金材料处于极限参数状态,因此在建立数据集时将极限状态组合剔除,以防止产生的异常数据对预测模型产生干扰。表3中的25组正交试验数据并不存在极限参数组合,将其作为样本数据,利用MATLAB中的nlinfit函数建立非线性回归模型。根据第2.2.2节显著性分析结果,将显著性较低项进行剔除,即E×n、E×A、B×n和E×B4个交互作用项,得到G1、G2、G3、G4铆接干涉量多元非线性回归预测模型如下 1.340 7×10-6x2x3-0.001 9x2x4 (6) 3.721 3×10-7x2x3-6.563×10-4x2x4 (7) 6.161 9×10-4x2x4 (8) 0.001 8x2x4 (9) 式中:x1、x2、x3、x4分别代表E、A、B和n的数据值。 通过建立的4个多元非线性预测模型,可以求出在确定工艺条件下G1、G2、G3和G4无头铆钉安装干涉量的预测值。由于预测模型是基于五水平-无交互作用正交试验数据建立的,因此本节选用另一组二水平-有交互作用的正交试验数据进行验证分析,其中试验2、7、10和15中的材料参数组合处于极限位置状态,将其剔除。 利用有限元分析得到的正交试验数据与通过回归模型求出的预测数据进行对比,结果见图7。由图7可以看出,回归模型预测值与仿真模拟值趋势变化一致,且预测误差都不超过10%,表明建立的多元非线性回归模型可以有效预测G1、G2、G3和G4无头铆钉安装干涉量水平。本文预测模型可以通过输入连接件材料参数得到相应的干涉量预测值,若在铆接过程中铆钉材料或工艺条件发生变化,只需在有限元建模过程中对铆钉材料属性及载荷设定进行相应地改变,并重复正交实验以及预测模型构建过程即可得到相应的无头铆钉安装干涉量预测模型。这表明本文预测方法具有较高普适性。 (b)G2 (c)G3 (d)G4 本文采用有限元正交模拟方法研究了被连接件材料性能参数对干涉量的影响规律,建立了无头铆钉安装干涉量多元非线性回归预测模型,研究的主要结论如下。 (1)在确定铆接工艺条件下,屈服强度对干涉量的影响最大且呈负相关,应变强度指数影响次之且呈正相关,而弹性模量和强化系数相较于屈服强度来说影响较弱。 (2)在两因素交互影响中,屈服强度跟应变强度指数和强化系数的交互作用影响具有高度显著性,甚至高于个别单一因素的影响作用。因此,在进行铆接干涉量的影响研究时,不应忽略各因素间的交互作用。 (3)基于显著性分析研究结果建立了G1、G2、G3和G4干涉量回归预测模型,验证结果表明,模拟值与预测值之间趋势变化一致,误差范围小于10%,表明回归预测模型对干涉量预测具有有效性,为实际铆接试验提供了理论指导。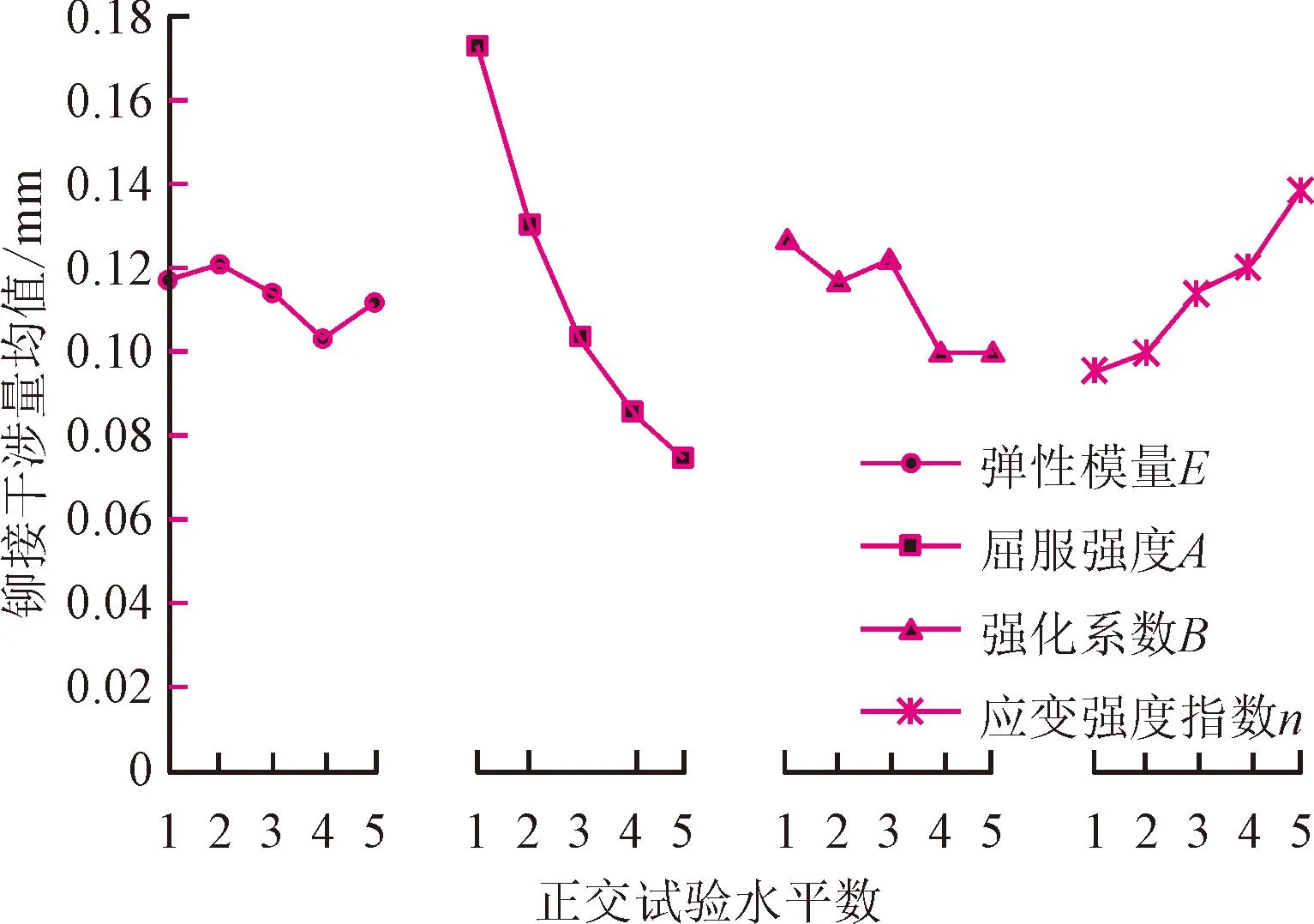
2.2 考虑因素间交互作用的正交试验


3 无头铆钉安装干涉量预测建模
3.1 多元非线性回归预测模型构建
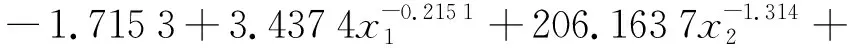
3.2 多元非线性回归预测模型验证


4 结 论
