俯冲板块脱水相变对板块俯冲过程的影响

王瑞泽, 王建超, 金宗玮, 刘骏标, 王雪纯, 靳国栋, 邢会林, 2*

俯冲板块脱水相变对板块俯冲过程的影响

王瑞泽1, 王建超1, 金宗玮1, 刘骏标1, 王雪纯1, 靳国栋1, 邢会林1, 2*

(1. 深海圈层与地球系统教育部前沿科学中心, 海底科学与探测技术教育部重点实验室, 中国海洋大学 海洋地球科学学院, 山东 青岛 266100; 2. 崂山实验室, 山东 青岛 266237)

板块俯冲是地球上最重要的动力学过程之一, 关于俯冲带相变对地幔楔和上覆板块影响前人已开展大量研究, 但关于相变反应对俯冲板块的动力学影响研究较少。本研究在拉格朗日积分点有限元代码的基础上, 实现了俯冲板块的相变, 建立了二维自由俯冲模型, 研究了俯冲过程中俯冲板块上矿物脱水相变对俯冲速度、俯冲板块形态、板块上的应力变化的影响。同时我们研究了薄弱带的黏度变化对俯冲起始与俯冲过程的影响。数值模拟实验结果显示: ①俯冲板块脱水相变现象的发生降低了板块俯冲的速度, 改变了俯冲板块的形态, 在俯冲板块的相变界面处发生应力累积; ②相较于矿物相变导致的黏度增大, 俯冲起始角度仍是影响俯冲板块俯冲速度的主要因素; ③薄弱带黏度越高越不利于俯冲板块与上覆板块的解耦, 抑制了俯冲过程的进行。该研究为探究板块回卷的控制因素以及俯冲板块应力状态变化的影响因素提供了新的视角。

俯冲板块; 俯冲过程; 矿物相变; 有限元数值模拟

0 引 言

俯冲带是地幔对流单元的下降分支, 是地球内部占主导地位的物理和化学系统, 也是地球上最大的“回收系统”(Stern, 2002)。俯冲板块将远洋陆源沉积物、蚀变的和新鲜的玄武质洋壳物质以及地幔岩石圈等“原材料”运送到俯冲带, 使海洋岩石圈、沉积物和海水与周围的地幔物质发生熔融, 重新平衡(Tatsumi, 2005)。

随着俯冲深度的增加, 俯冲带中温度和压力不断增大。俯冲带热力学模拟是研究俯冲带热结构最好的方法, 通过计算发现板块在俯冲过程中被高温的地幔加热(Peacock and Wang, 1999; Gerya et al., 2002; Gorman et al., 2006; Syracuse et al., 2010)。同时, 研究证明, 在高温高压条件下, 俯冲板块中矿物主要发生两类相变反应: 一类为俯冲板块上深度较浅的玄武岩‒榴辉岩系列相变(Schmidt and Poli, 1998; Fryer et al., 1999; Forneris and Holloway, 2003; Forneris and Holloway, 2004); 另一类则是发生在俯冲地幔以及俯冲板块上覆地幔楔中的橄榄岩‒蛇纹岩‒橄榄岩系列相变。蛇纹石化是一个重要的地球动力学过程, 它极大地改变了地幔和洋壳的物理和力学性质。蛇纹岩是由超基性岩和基性岩在俯冲带浅部、低温(100 ℃)‒中温(700 ℃)条件下水合而成(Bose and Ganguly, 1995;Ulmer and Trommsdorff, 1995; Kawamoto and Holloway, 1997; Grove et al., 2006; Till et al., 2012; Green et al., 2014)。随着俯冲深度的增加, 在高温高压条件下, 蛇纹岩失稳发生脱水相变反应, 形成橄榄石与其他矿物组合(Ulmer and Trommsdorff, 1995; Wunder and Schreyer, 1997; Evans, 2004; Perrillat et al., 2005; Schwartz et al., 2013; Guillot et al., 2015)。

由于俯冲带岩石样品获取难度较大, 而实验又难以解决俯冲过程中复杂的地质问题。随着计算机技术的进步, 数值模拟可以有效地解决地质问题中存在的时空尺度局限性问题, 因此许多学者通过数值模拟手段对俯冲带的相变反应及其影响进行了研究。Gerya et al. (2002)结合前人岩石学成果, 基于有限差分方法, 针对俯冲通道的发展和地幔楔水化作用这一问题进行了模拟研究; Arcay et al. (2005)通过有限元数值模拟的方法, 研究俯冲板片脱水对地幔楔的影响; Wada et al. (2008)通过有限元数值模拟, 研究上覆板块与俯冲板块之间薄弱带以及板块脱水对地幔楔的影响; Gerya and Meilick (2011)通过有限差分程序, 研究俯冲带熔体和流体对流变性质的影响, 以及其对俯冲动力学的影响; Faccenda et al. (2012)基于有限差分方法, 研究板块相变脱水对中‒深地震活动、板块弱化和深部水循环的影响; Liao et al. (2017)利用同样的方法, 研究水化作用引起的上地幔弱化对克拉通岩石圈动力学的影响。

尽管前人对俯冲板块的相变过程以及相变脱水对地幔物质的影响进行了大量研究, 但主要侧重于相变反应对地幔楔以及上覆板块的影响, 而很少考虑俯冲过程中矿物脱水相变对俯冲板块动力学行为的影响(Schellart et al., 2010; Sandiford et al., 2019)。为了充分研究板块俯冲至平衡深度时发生蛇纹岩岩石圈地幔相变对俯冲速度、俯冲板片形态的影响, 以及对俯冲板块应力应变状态的影响, 本次研究基于有限元数值模拟方法, 通过构建俯冲板块自由俯冲模型, 对俯冲板块中各种材料参数进行设置, 对板块俯冲过程进行模拟, 并结合前人研究成果, 进一步讨论矿物相变对板块俯冲的影响。

1 控制方程

1.1 有限元部分

通过求解稳态不可压缩蠕动流的斯托克斯方程进行数值模拟。

其中质量守恒方程为:

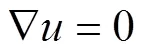
动量守恒方程为:

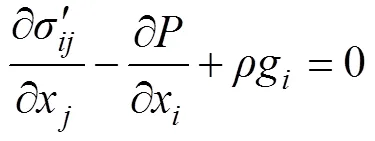
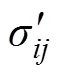
对于不可压缩流, 可通过公式(3)计算偏应力张量:

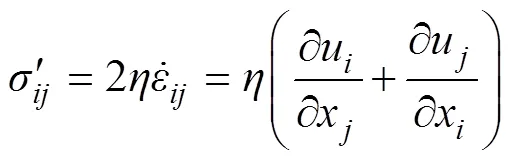
本次研究采用拉格朗日积分点有限元法进行有限元数值模拟计算。拉格朗日积分点有限元法主要优点在于: ①能在不显著改变精度的情况下继续进行极大变形; ②能够跟踪材料历史和界面, 其精度高; ③在整个运行过程中保留规则网格, 可以使用快速数值求解器。求解域由欧拉网格和嵌入的拉格朗日追踪点或粒子表示, 未知变量在网格节点上计算, 拉格朗日粒子在变形过程中携带历史变量。该方法非常适合于模拟地质环境中经常遇到的连续介质固体的类流体行为, 能够对包括地幔对流、板块俯冲和大陆碰撞在内的构造过程进行二维/三维热‒变形‒化学反应建模(Moresi et al., 2003, 2007)。

1.2 相变部分

叶蛇纹石是俯冲带高温高压蛇纹石的变种, 是深度大于100 km俯冲带中最主要的含水矿物, 俯冲带中主要脱水相变过程(图1)(Guillot et al., 2015)为

图1 根据实验数据和天然蛇纹石岩石学观测得出的蛇纹石稳定场(Perrillat et al., 2005; Guillot et al., 2015)

Fig.1 Serpentine stability fields based on experimental data and natural serpentine lithological observations

据Carminati et al. (1999)和Schwartz et al. (2001)的研究, 俯冲带蛇纹岩脱水相变会导致岩石流变强度变大。本次研究基于有限元理论、固定的计算网格和拉格朗日积分点法的程序Underworld, 通过判断板块上的追踪粒子是否发生相变进而改变材料黏度, 在程序中实现了俯冲板片上蛇纹岩脱水相变这一过程(图2)。

图2 相变部分算法计算流程图

Fig.2 The algorithm flow chart of phase transition

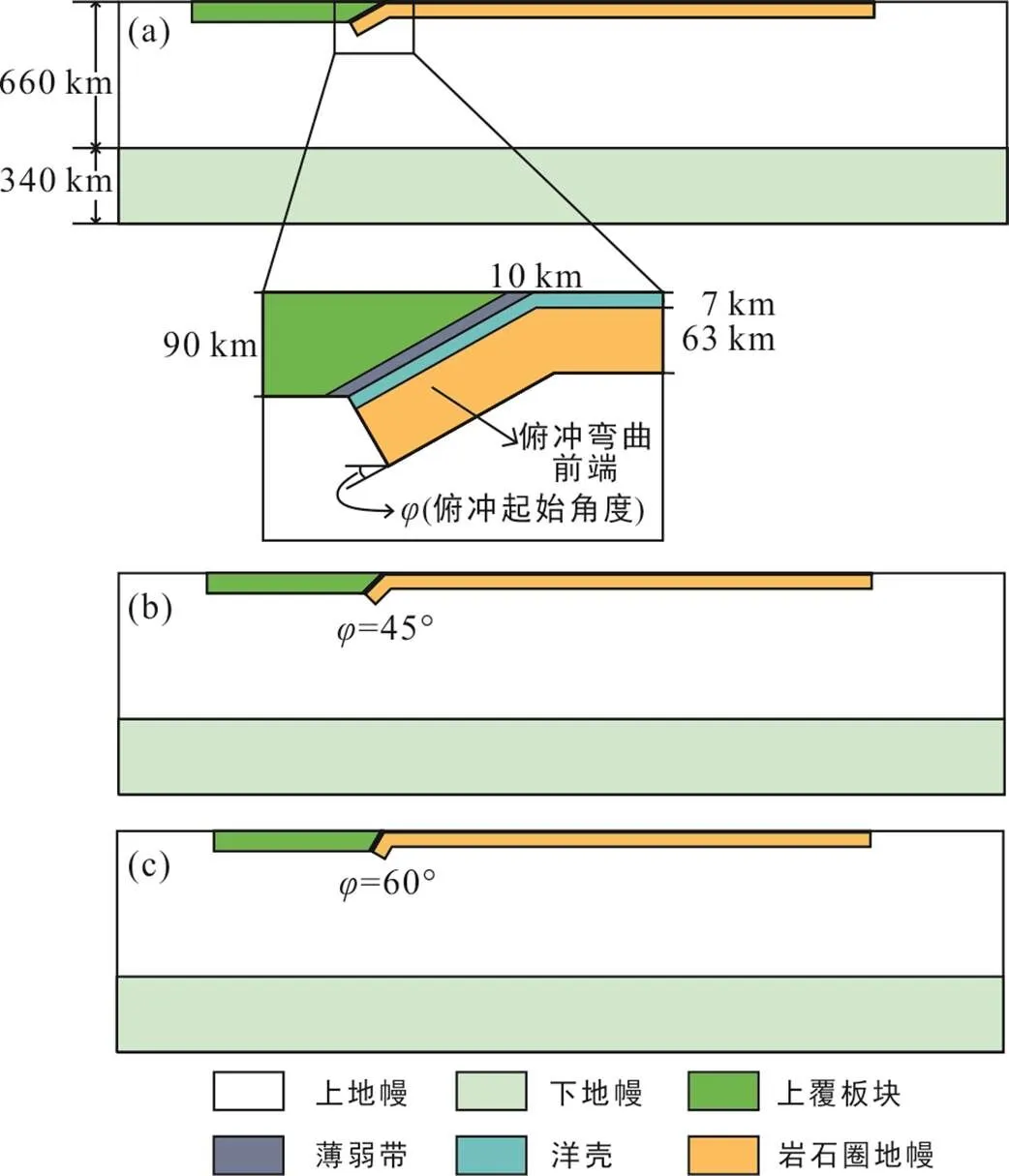
图3 不同俯冲起始角度模型几何示意图

2 模型设置

2.1 模型的几何和流变学

在海洋板块弯曲前端与大陆板块之间设置宽度约10 km的薄弱带, 初始模型中黏度设置为上地幔黏度的十分之一, 上覆板块厚度设置为90 km, 与俯冲板块俯冲起始深度相同。本次模拟实验只考虑主要的相变过程(即蛇纹岩中叶蛇纹石失稳脱水相变, 形成橄榄石为主以及少量蛇纹石的岩石组分)对俯冲板块的流变学性质的影响, 模型中各种材料参数如表1所示。

表1 模型使用材料参数表

2.2 边界条件

本研究假设成熟洋板块和上地幔之间的重力不稳定性导致了俯冲板块的下沉, 俯冲是由板块前端的弯曲尖端触发。在模型的边界施加自由滑动速度边界。因此, 只有负浮力(板块拉张)才能驱使海洋板块俯冲, 诱发地幔流动, 没有速度或应力施加到俯冲板块或上覆板块上。

2.3 模型设计

本模拟设置了俯冲起始角度为30°的对照组模型1～2, 不同俯冲起始角度的实验组模型3～6(表2)。对照组为在重力作用下板块发生俯冲, 俯冲过程中俯冲板块、上地幔等不同材料的黏度保持不变; 实验组为在重力作用下板块发生俯冲, 在俯冲至固定深度时, 俯冲板块会发生相应的相变, 从而导致黏度变化。本次研究主要探究板块俯冲过程中相变对俯冲板块内应力场的变化、俯冲板块的动力学行为的影响。同时根据模拟结果, 增设两组模型以探讨不同的薄弱带黏度对俯冲板块俯冲的影响(模型7、8), 以及两组模型以探讨不同薄弱带宽度对俯冲板块俯冲过程的影响(模型9、10)。

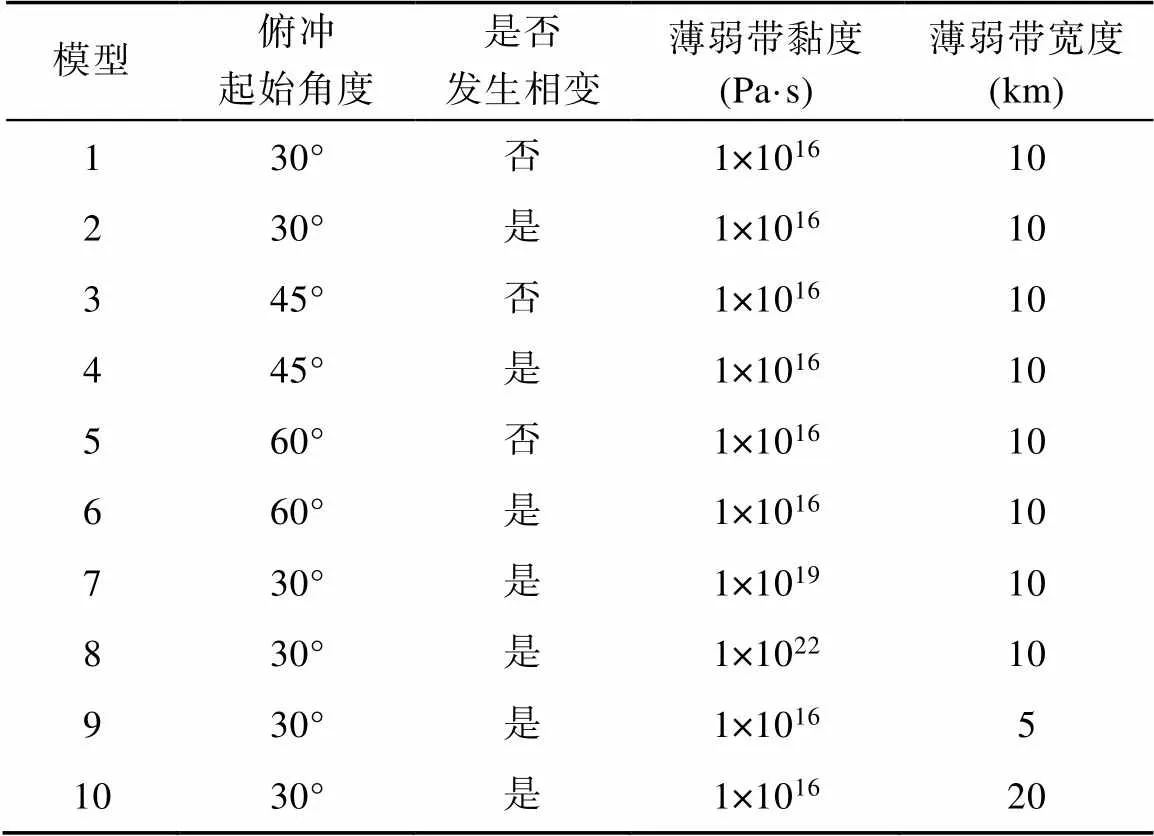
表2 模型参数设置表

3 结果分析

3.1 俯冲过程分析(模型1、2)

板块俯冲运动是由板块自身重力和克服板块底部黏滞阻力的能力决定的, 其中下降板的负浮力是板块运动的主要动力。板块的自由俯冲模型结果显示俯冲具有两个阶段。

阶段一: 由于地幔和大洋板块之间的重力不稳定, 大洋板块从预先设置的俯冲弯曲前端扰动处开始俯冲(图4a、e)。随着板块俯冲, 上覆板块持续向海沟方向后退。上地幔在俯冲作用下发生扰动, 以平行于俯冲板块下方海沟的方向运动(图4b、d、f、g)。俯冲板块后撤引起的水平向地幔角流既驱动上覆板块向海沟侧运动, 同时也拖拽俯冲板块持续向下俯冲(Zhang et al., 2017)。阶段二: 在俯冲进行一段时间后, 自由俯冲模型中的俯冲板块在重力作用下以接近90°向地幔深处俯冲(图4d、h)。

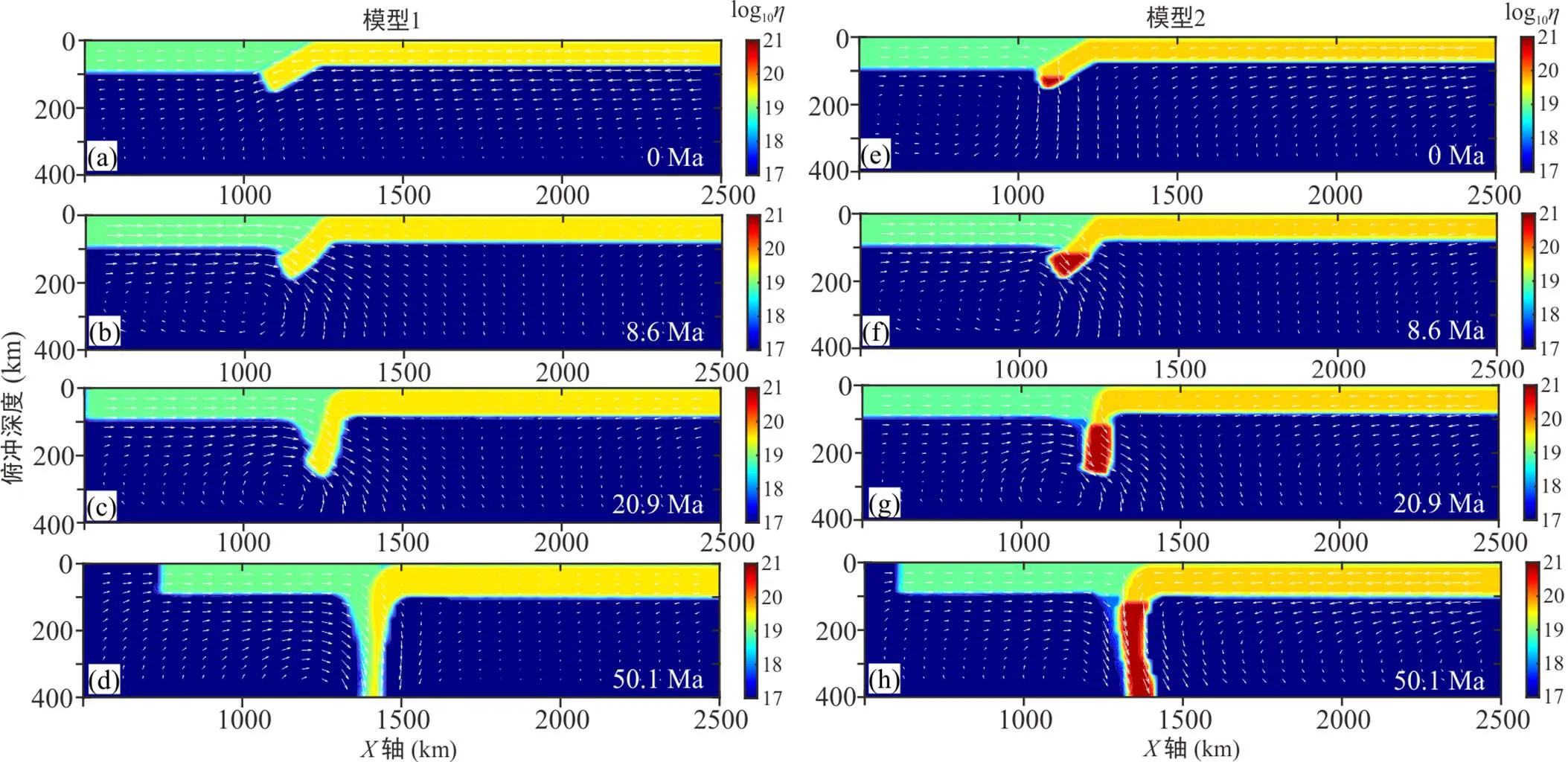
(a)～(d) 为板块未发生相变俯冲至50 Ma结果图; (e)～(h) 为板块发生相变俯冲至50 Ma结果图。白色箭头标记为均方根速度(Vrms)。

当俯冲起始角度为30°时, 岩石圈地幔未发生相变时, 整个俯冲板块黏度均匀, 因此整个板块俯冲趋势保持一致。俯冲弯曲前端在自身重力的作用下, 俯冲角度由起始时的30°逐渐变为90°垂直向下俯冲。若在模型中添加俯冲过程中蛇纹石化岩石圈地幔的相变反应后, 俯冲过程则变得有所不同。由于大洋岩石圈在俯冲过程中发生了相变, 导致黏度变大, 进而使得俯冲更难以进行, 因此俯冲角度从30°至90°所需时间明显少于未发生相变的模型。

3.2 蛇纹石化岩石圈地幔相变对俯冲速度的影响

为了研究不同俯冲起始角度对俯冲速度的影响, 以及蛇纹石化岩石圈地幔发生相变对俯冲速度带来的影响, 本次研究设置了模型3～6。首先, 设定俯冲起始角度为30°, 俯冲至同一时刻发生相变与未发生相变的模型(模型1、2), 并进行了均方根速度成图(图5)。结果显示, 板块俯冲至相同时刻下, 未发生相变的模型中俯冲板块处的均方根速度明显大于发生相变模型。由于板块俯冲是在板块的负浮力以及板块与地幔之间的黏滞阻力共同作用下完成的, 而发生相变俯冲板块底部需要克服的黏滞阻力变大, 导致俯冲板块俯冲速度变小。

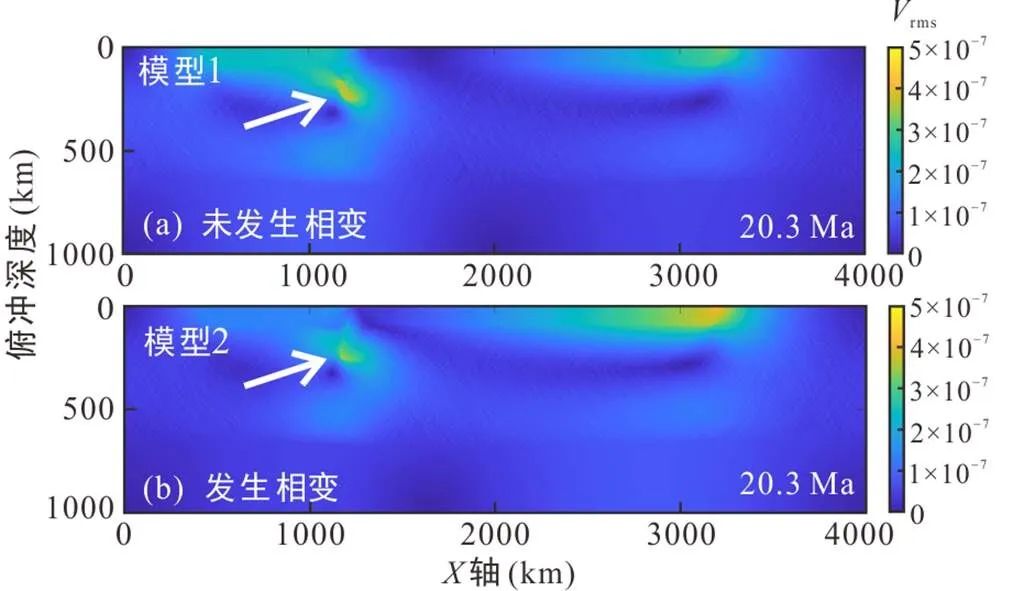
图5 俯冲起始角度为30°模型俯冲至20.3 Ma时均方根速度图

模拟中通过追踪不同俯冲起始角度以及是否发生相变影响下, 各组模型俯冲板块最底部粒子所在深度, 得到模型1～6俯冲深度与时间的关系。通过对未发生相变、俯冲起始角度不同的模型1、3、5进行分析(图6), 结果显示,在相同俯冲时间内, 俯冲起始角度为30°的模型俯冲速度最快, 随着俯冲起始角度的增加, 俯冲速度相应变慢。在相同的俯冲时间内, 俯冲起始角度越小, 俯冲板块俯冲所能达到的深度越深。

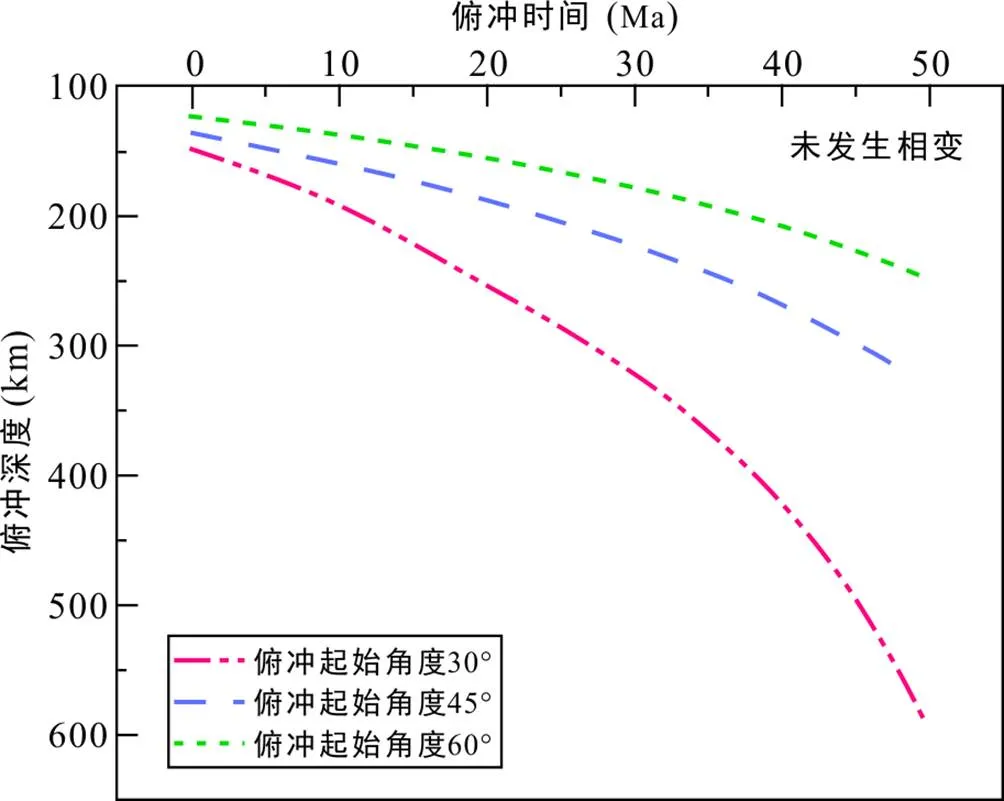
图6 不同俯冲起始角度未发生相变模型俯冲速度图

发生相变、俯冲起始角度不同的模型2、4、6俯冲深度随俯冲时间变化的结果(图7)显示, 板块相变在一定程度上影响了板块俯冲的速度, 导致板块俯冲速度变慢。但是随着俯冲起始角度的增大, 板块相变对俯冲速度的影响逐渐减小, 因此, 俯冲起始角度是控制俯冲板块俯冲速度的主要因素。

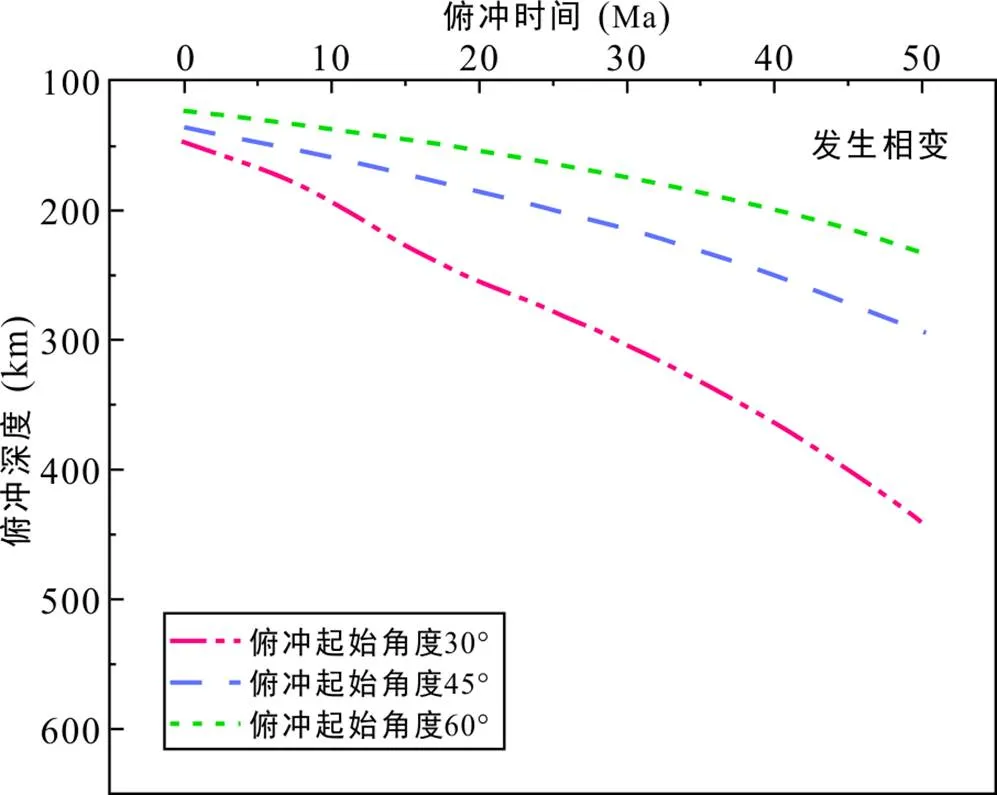
图7 不同俯冲起始角度发生相变模型俯冲速度图

3.3 俯冲过程应力变化分析

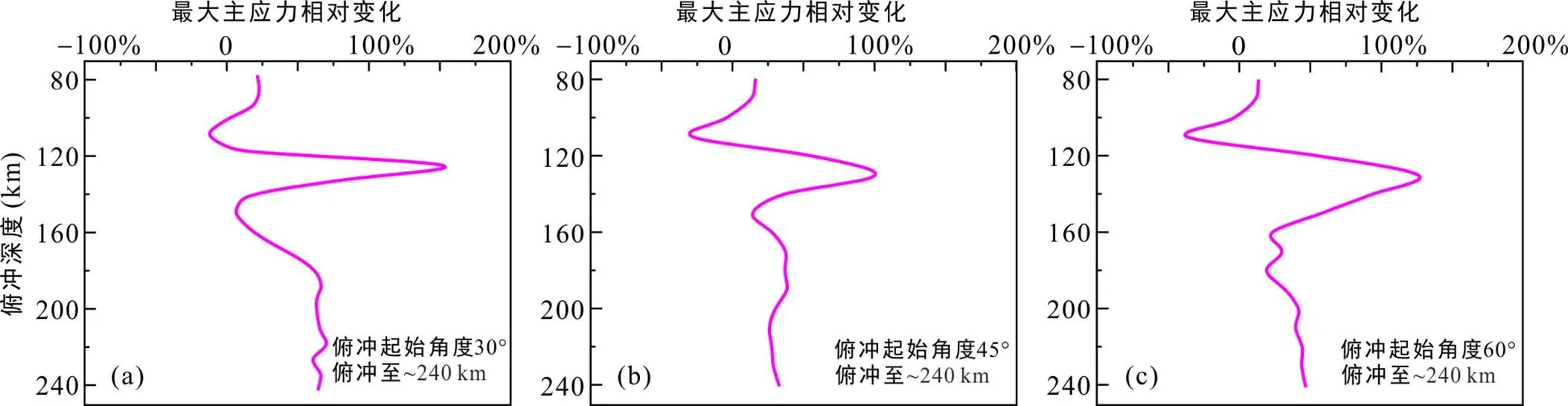
图8 不同俯冲起始角度发生相变与未发生相变模型板块上最大主应力的相对变化

3.4 薄弱带作用结果

为了研究薄弱带的黏度和宽度在俯冲过程中的作用, 本次研究设置了模型7～10。当模型中薄弱带固定宽度为10 km, 薄弱带黏度为低于俯冲板块与上覆板块的黏度1×1016Pa·s时, 俯冲板块弯曲前端可以较快速的与上覆板块发生解耦, 在自身重力的作用下, 耗时约23 Ma进入俯冲角度近乎90°的垂直俯冲阶段, 并在俯冲后期发生板块回卷现象(图4h)。而增设两组更大黏度的模型7和模型8则表明, 随着薄弱带流变强度增大, 俯冲角度从起始的30°变化至90°所需的时间变长。其中薄弱带黏度为1×1019Pa·s的模型7(图9a、b); 即薄弱带不存在, 俯冲洋壳与流变强度相同的上覆地壳直接接触时, 耗时约28 Ma变为俯冲角度接近90°的垂直向下俯冲; 而薄弱带黏度为1×1022Pa·s的模型8(图9c、d), 则在俯冲角度俯冲至约45°时, 俯冲趋势就被上部高黏度的薄弱带所抑制, 黏度比俯冲板块和上覆板块高的薄弱带不利于俯冲板块与上覆板块之间的解耦, 抑制了俯冲过程的进行。

图9 不同薄弱带黏度设置下板块俯冲模型黏度场与速度场

为探究不同的薄弱带宽度对俯冲过程的影响, 本次研究增设了薄弱带宽度为5 km的模型9和薄弱带宽度为20 km的模型10。结果显示, 在薄弱带黏度固定为1×1016Pa·s时, 薄弱带宽度增大时, 板块俯冲速度明显增大(图10)。通过对比不同薄弱带宽度模型中俯冲起始角度由30°变为垂直俯冲阶段所用的时间, 显示薄弱带宽度为20 km时, 所需的时间约为15 Ma; 薄弱带宽度为10 km时, 所需时间约为23 Ma; 薄弱带宽度为5 km时, 所需时间约为27 Ma。因此, 薄弱带黏度固定且为较低黏度时, 薄弱带宽度越大, 俯冲板块与上覆板块之间解耦越快。

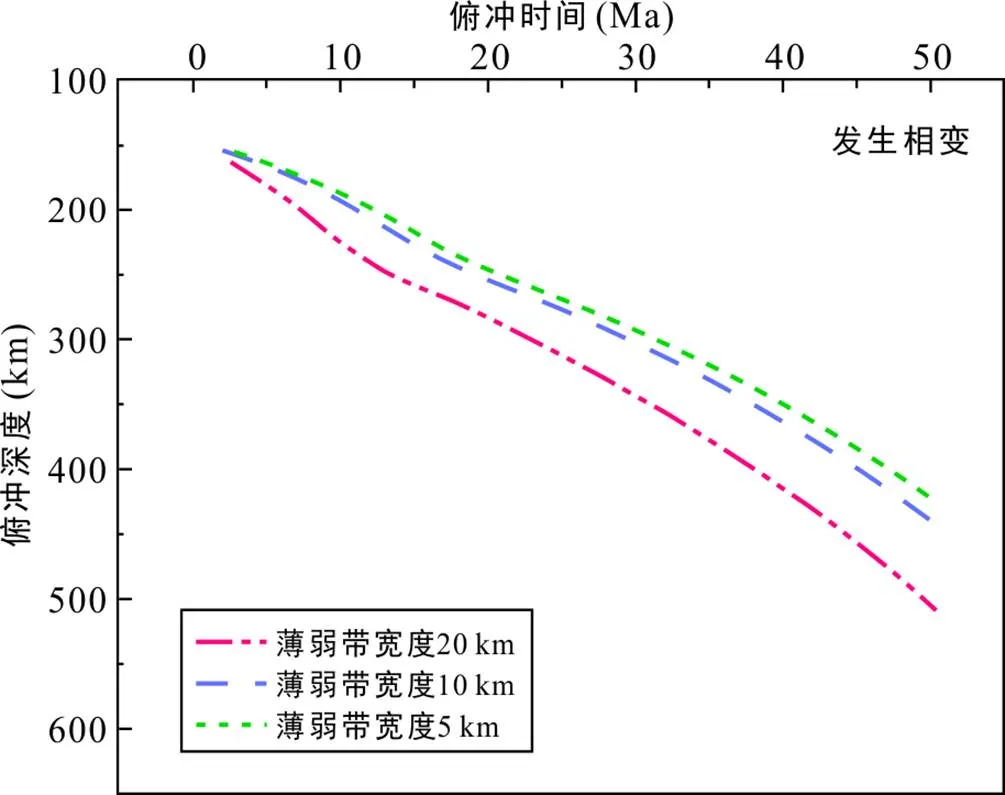
图10 不同薄弱带宽度下发生相变模型俯冲速度图

4 讨 论

本次研究在拉格朗日积分点有限元方法的基础上, 添加了与俯冲板块蛇纹岩脱水相变相关的代码, 研究了矿物相变对俯冲过程产生的一系列影响。但是由于本次研究的模型中只考虑材料黏度变化对俯冲板块的影响, 因此只考虑了俯冲板块中蛇纹岩脱水相变导致的黏度差异对俯冲过程的影响, 而认为俯冲板块中大洋中脊玄武岩系列的相变反应对俯冲板块的影响较小。

4.1 板块俯冲形态

在前人研究的基础上(Zhang et al., 2017), 选择的基础模型为自由俯冲模型, 没有额外恒定的边界条件, 所以板块不能保持倾角恒定的持续俯冲, 表现出俯冲角度从30°逐渐向90°增加。而在模型2中, 由于俯冲板块120 km以下板块发生相变, 俯冲角度变化更大, 出现类似于Perchuk et al. (2020)模拟结果中的板块回卷现象(图4h)。前人研究认为榴辉岩化导致的重力异常是引起板块回卷的主要原因之一(孙圣思和嵇少丞, 2011; 皇甫鹏鹏等, 2016; Dai et al., 2020)。而在本次模拟中由于设定密度固定不变, 只有板块俯冲至一定深度时黏度发生变化, 俯冲板块才会发生了类似板块回卷现象, 所以俯冲板块相变导致板块黏度变大可能也是导致板块回卷现象的原因之一。

4.2 板块应力变化

模拟结果显示, 板块俯冲至不同深度时, 在板块发生相变的界面处出现应力集中导致应力陡变。应力集中出现的原因是在俯冲过程中, 俯冲板块相变导致黏滞力增大, 因此板块自相变界面以下部分俯冲速度降低, 发生了短暂的停滞。Kita et al. (2006)发现日本东北部下方70～100 km深度处双地震带上平面存在带状地震活动集中区, 并将其解释为与Hacker et al. (2003)模拟的相边界附近的脱水反应有关; Tsuji et al. (2008)利用双差层析成像技术, 估算出日本东部太平洋板块下一个厚度约为10 km的含水低速带在70～90 km处逐渐发生脱水消失。本次模拟结果也证实了相变界面处发生了应力集中。因此, 俯冲板块黏度变化导致的应力集中可能是导致双地震带上形成带状地震活动集中区的原因之一。

4.3 薄弱带的影响

俯冲带的数值模拟实验中, 俯冲洋壳和上覆板块之间的薄弱带黏度的大小会影响板块速度(Androvičová et al., 2013; Holt et al., 2015), 较高黏度的薄弱带会抑制板块回卷现象的发生(Arredondo and Billen, 2017)。因此, 俯冲洋壳和上覆板块的解耦对俯冲板块深部变形具有很强的敏感性。如图4h、9b、9d所示, 较低的薄弱带黏度导致板块回卷较容易发生, 而较强的薄弱带黏度导致板块回卷现象难以发生。同时, 薄弱带的宽度也会对俯冲板块与上覆板块的解耦产生影响, 在薄弱带黏度较低时, 越宽的薄弱带越有利于俯冲板块与上覆板块的解耦。

5 结 论

本次研究通过在拉格朗日积分点有限元代码中添加俯冲板块矿物相变部分, 建立俯冲板块自由俯冲相变模型, 模拟了相变对俯冲板块的动力学行为与应力状态的影响, 以及不同的俯冲角度与薄弱带对俯冲过程的影响, 得到以下几点认识:

(1) 矿物相变导致了俯冲板块上发生相变的部分黏度变大, 进而使板块俯冲需要克服的板块底部黏滞阻力变大, 从而降低了板块俯冲的速度, 改变了俯冲板块的俯冲形态, 同时在俯冲板块的相变界面处发生应力累积。

(2) 虽然俯冲板块上相变降低了其俯冲速度, 但俯冲起始角度才是影响俯冲板块俯冲速度的主要因素。

(3) 当薄弱带宽度一定时, 黏度较低的薄弱带有利于上覆板块与俯冲板块之间的解耦, 薄弱带黏度越高越不利于俯冲板块与上覆板块的解耦, 在一定程度上抑制俯冲过程的进行; 当薄弱带黏度(较低黏度)一定时, 薄弱带的宽度越大越有利于俯冲板块与上覆板块的解耦, 反之则会对俯冲过程起到抑制作用。

致谢:中国科学院广州地球化学研究所郭锋研究员及另一名匿名审稿人对本文提出了建设性修改意见, 在此致以特别感谢。

皇甫鹏鹏, 王岳军, 范蔚茗, 李忠海, 王喻鸣, 周永智. 2016. 大洋平板俯冲的数值模拟再现: 洋‒陆汇聚速率影响. 大地构造与成矿学, 40(3): 429–445.

李三忠, 王光增, 索艳慧, 李玺瑶, 戴黎明, 刘一鸣, 周洁, 郭玲莉, 刘永江, 张国伟. 2019. 板块驱动力: 问题本源与本质. 大地构造与成矿学, 43(4): 605–643.

孙圣思, 嵇少丞. 2011. 大洋板块俯冲带地震波各向异性及剪切波分裂的成因机制. 大地构造与成矿学, 35(4): 628–647.

Androvičová A, Čížková H, van den Berg A. 2013. The effects of rheological decoupling on slab deformation in the Earth’s upper mantle., 57(3): 460–481.

Arcay D, Tric E, Doin M. 2005. Numerical simulations of subduction zones: Effect of slab dehydration on the mantle wedge dynamics., 149(1–2): 133–153.

Arredondo K M, Billen M I. 2017. Coupled effects of phase transitions and rheology in 2-D dynamical models of subduction.:, 122(7): 5813–5830.

Bose K, Ganguly J. 1995. Experimental and theoretical studies of the stabilities of talc, antigorite and phase A at high pressures with applications to subduction processes., 136(3–4): 109–121.

Carminati E, Giunchi C, Argnani A, Sabadini R, Fernandez M. 1999. Plio-Quaternary vertical motion of the Northern Apennines: Insights from dynamic modeling., 18(4): 703–718.

Cloos M. 1993. Lithospheric buoyancy and collisional orogenesis: Subduction of oceanic plateaus, continental margins, island arcs, spreading ridges, and seamounts., 105(6): 715–737.

Dai L M, Wang L L, Lou D, Li Z H, Dong H, Ma F F, Li F K, Li S Z, Yu S Y. 2020. Slab rollback versus delamination: Contrasting fates of flat-slab subduction and implicationsfor South China evolution in the Mesozoic.:, 125(4), e2019JB019164.

Duretz T, Gerya T V, May D A. 2011. Numerical modelling of spontaneous slab breakoff and subsequent topographic response., 502(1): 244–256.

Evans B W. 2004. The serpentinite multisystem revisited: Chrysotile is metastable., 46(6): 479–506.

Faccenda M, Gerya T V, Mancktelow N S, Moresi L. 2012. Fluid flow during slab unbending and dehydration: Implications for intermediate-depth seismicity, slab weakening and deep water recycling.,,, 13(1), Q01010.

Forneris J F, Holloway J R. 2003. Phase equilibria in subductingbasaltic crust: Implications for H2O release from the slab., 214(1–2): 187–201.

Forneris J F, Holloway J R. 2004. Evolution of mineral compositions during eclogitization of subducting basaltic crust., 89(10): 1516–1524.

Fryer P, Wheat C G, Mottl M J. 1999. Mariana blueschist mud volcanism: Implications for conditions within the subduction zone., 27(2): 103–106.

Gerya T V, Meilick F I. 2011. Geodynamic regimes of subduction under an active margin: Effects of rheologicalweakening by fluids and melts., 29(1): 7–31.

Gerya T V, Stöckhert B, Perchuk A L. 2002. Exhumation of high-pressure metamorphic rocks in a subduction channel: A numerical simulation., 21(6), 1056.

Gerya T V, Yuen D A. 2003. Rayleigh-Taylor instabilities from hydration and melting propel ‘cold plumes’ at subduction zones., 212(1): 47–62.

Gorman P J, Kerrick D M, Connolly J. 2006. Modeling open system metamorphic decarbonation of subducting slabs.,,, 7(4), Q04007.

Green D H, Hibberson W O, Rosenthal A, Kovács I, Yaxley G M, Falloon T J, Brink F. 2014. Experimental study of the influence of water on melting and phase assemblagesin the upper mantle., 55(10): 2067– 2096.

Grove T L, Chatterjee N, Parman S W, Médard E. 2006. The influence of H2O on mantle wedge melting., 249(1–2): 74–89.

Guillot S, Schwartz S, Reynard B, Agard P, Prigent C. 2015. Tectonic significance of serpentinites., 646: 1–19.

Hacker B R, Peacock S M, Abers G A, Holloway S D. 2003. Subduction factory 2. Are intermediate-depth earthquakes in subducting slabs linked to metamorphic dehydration reactions?:, 108(B1), ESE11.

Holt A F, Becker T W, Buffett B A. 2015. Trench migration and overriding plate stress in dynamic subduction models., 201(1): 172–192.

Kawamoto T, Holloway J R. 1997. Melting temperature and partial melt chemistry of H2O-saturated mantle peridotite to 11 gigapascals., 276(5310): 240–243.

Kita S, Okada T, Nakajima J, Matsuzawa T, Hasegawa A. 2006. Existence of a seismic belt in the upper plane of the double seismic zone extending in the along-arc direction at depths of 70–100 km beneath NE Japan., 33(24), L24310.1- L24310.5.

Korenaga T, Korenaga J. 2016. Evolution of young oceanic lithosphere and the meaning of seafloor subsidence rate.:, 121(9): 6315–6332.

Liao J, Wang Q, Gerya T, Ballmer M D. 2017. Modeling craton destruction by hydration-induced weakening of the upper mantle.:, 122(9): 7449–7466.

Moresi L, Dufour F, Mühlhaus H. 2003. A Lagrangian integrationpoint finite element method for large deformation modeling of viscoelastic geomaterials., 184(2): 476–497.

Moresi L, Quenette S, Lemiale V, Meriaux C, Appelbe B, Mühlhaus H B. 2007. Computational approaches to studying non-linear dynamics of the crust and mantle., 163(1–4): 69–82.

Peacock S M, Wang K, 1999. Seismic consequences of warm versus cool subduction metamorphism: Examples from southwest and northeast Japan., 286(5441): 937–939.

Perchuk A L, Gerya T V, Zakharov V S, Griffin W L. 2020. Building cratonic keels in Precambrian plate tectonics., 586(7829): 395–401.

Perrillat J P, Daniel I, Koga K T, Reynard B, Cardon H, Crichton W A. 2005. Kinetics of antigorite dehydration: A real-time X-ray diffraction study., 236(3–4): 899–913.

Sandiford D, Moresi L, Sandiford M, Yang T. 2019. Geometric controls on flat slab seismicity., 527: 115787.

Schellart W P, Stegman D R, Farrington R J, Freeman J, Moresi L. 2010. Cenozoic tectonics of western North America controlled by evolving width of Farallon slab., 329(5989): 316–319.

Schmidt M W, Poli S. 1998. Experimentally based water budgets for dehydrating slabs and consequences for arc magma generation., 163(1–4): 361–379.

Schwartz S, Allemand P, Guillot S. 2001. Numerical model of the effect of serpentinites on the exhumation of eclogitic rocks: Insights from the Monviso ophiolitic massif (Western Alps)., 342(1–2): 193–206.

Schwartz S, Guillot S, Reynard B, Lafay R, Debret B, Nicollet C, Lanari P, Auzende A L. 2013. Pressure- temperature estimates of the lizardite/antigorite transition in high pressure serpentinites., 178: 197–210.

Stern R J. 2002. Subduction zones., 40(4): 3–1.

Syracuse E M, van Keken P E, Abers G A. 2010. The global range of subduction zone thermal models., 183(1–2): 73–90.

Tatsumi Y. 2005. The subduction factory: How it operates in the evolving Earth., 15(7): 4.

Till C B, Grove T L, Withers A C. 2012. The beginnings of hydrous mantle wedge melting., 163(4): 669–688.

Tsuji Y, Nakajima J, Hasegawa A. 2008. Tomographic evidence for hydrated oceanic crust of the Pacific slab beneath northeastern Japan: Implications for water transportation in subduction zones., 35(14), L14308.

Ulmer P, Trommsdorff V. 1995. Serpentine stability to mantle depths and subduction-related magmatism., 268(5212): 858–861.

Wada I, Wang K, He J, Hyndman R D. 2008. Weakening of the subduction interface and its effects on surface heat flow, slab dehydration, and mantle wedge serpentinization.:, 113(B4), B04402.

Wunder B, Schreyer W. 1997. Antigorite: High-pressure stability in the system MgO-SiO2-H2O (MSH)., 41(1–3): 213–227.

Zhang Q W, Guo F, Zhao L, Wu Y M. 2017. Geodynamics of divergent double subduction: 3-D numerical modeling of a Cenozoic example in the Molucca Sea region, Indonesia.:, 122(5): 3977–3998.

Influence of Dehydration Phase Transition of Subducting Plate on the Process of Plate Subduction

WANG Ruize1, WANG Jianchao1, JIN Zongwei1, LIU Junbiao1, WANG Xuechun1, JIN Guodong1, XING Huilin1, 2*

(1. Frontiers Science Center for Deep Ocean Multispheres and Earth System, MOE Key Lab of Submarine Geosciences and Prospecting Techniques, College of Marine Geosciences, Ocean University of China, Qingdao 266100, Shandong, China; 2. Laoshan Laboratory, Qingdao 266237, Shandong, China)

Plate subduction is one of the most important dynamic processes on the earth. The influences of phase change in subduction zones on the mantle wedge and overriding plates have been studied extensively, but researches on the influences of phase change on the dynamics of subducting plates are rare. Based on the Lagrangian integration point finite element code, we implemented the phase change of the plate into the code and performed 2D free subduction modelling to simulate the process of subduction. We investigated the influence of dehydration-related phase change on the subduction speed, shape of the subducting plate, and change of the stress field of the plate during the subducting process. Meanwhile we studied the influence of the viscosity change of the weak zone on the initiation and process of subduction. Based on these experiments we concluded that: (1) The phase change caused by mineral dehydration of the subducting plate reduces the speed of plate subducting and changes the shape of the subducting plate, and leads to stress accumulation at the phase change interface of the subducting plate. (2) Compared with the increase in viscosity caused by mineral phase transitions, initial subducting angle is still the main factor affecting the subduction velocity of subducting plates. (3) The higher the viscosity of the weak zone, the more difficult the decoupling of the subducting plate and the overlying plate, and thus inhibiting the progress of the subduction process. The results of simulation provide a new perspective for us to explore the controlling factors of rollback and the influencing factors of changes in the stress state of the subducting plate.

subducting plate; subducting process; phase change; finite element simulation

2021-12-05;

2022-03-28

国家自然科学基金重大计划重点支持项目(92058211)、国家自然科学基金面上项目(52074251)、中央高校基本科研业务经费(842012003)和高等学校学科创新引智计划项目(B20048)联合资助。

王瑞泽(1997–), 男, 硕士研究生, 海洋地质专业。E-mail: ruize1997@163.com

邢会林(1965–), 男, 教授, 博士生导师, 主要从事超级计算地球科学理论、软件研发及其应用等研究。E-mail: h.xing@ouc.edu.cn

P541

A

1001-1552(2023)06-1232-010

10.16539/j.ddgzyckx.2023.06.003