不同运动参数对圆筒型FPSO 垂荡性能和附加质量的影响
2024-01-15余勇军王文杰刘利琴
余勇军,王文杰,李 焱,刘利琴
(1.天津大学水利仿真与安全国家重点实验室,天津 300072;2.大连船舶重工集团有限公司,辽宁 大连 116083)
南海海域油气资源极其丰富,是我国规模最大的海洋油气储存区,据不完全统计,已探明的石油资源有6.4 亿吨,天然气储量为1 亿立方米。FPSO是海洋石油勘探和采集的重要海洋装备之一,具有投资成本低、适应性强等优势[1]。较早时期,FPSO大多为旧船改造而成,其细长型结构承受更大的总纵弯曲载荷,可能发生更大的总纵变形。船型结构甲板承载能力较弱,不利于采油作业,且较大的横摇响应使得正常作业变得很困难。相比之下,圆筒型FPSO 由于其对称的结构,具有各向同性、无风向标效应[2]且纵摇性能较好,近几年间获得了较多关注。
与传统船型FPSO 相比,圆筒型FPSO 垂荡阻尼小、垂荡运动响应大且难以控制[3],是其走向工程应用亟待解决的一大难题。为此,许多学者尝试设计和改进圆筒型FPSO 的垂荡抑制结构来改善其阻尼性能。童波等[4]对比分析了多种不同类型阻尼结构的阻尼性能,结果表明倒U 型阻尼性能最佳。JI X J 等[5]提出了一种带有锥角的减动结构,研究了不同锥角和孔径对于圆筒型FPSO 垂荡性能的影响,发现孔径在一定程度上能提高阻尼性能。李晨等[6]对比分析了上扬边锋型和锯齿型的减动结构,结果表明锯齿型减动结构的阻尼效果更优。郝未南等[7]研究了多种垂荡抑制机构对圆筒型FPSO 阻尼和运动性能的影响,结果同样证实了锯齿能显著影响阻尼性能和流场。陈维等[8]设计了具有通海形式的延伸筒体与减动结构的新型圆筒型FPSO,来解决垂荡性能差的问题。白杰等[9]提出了一种带间隙和外板边锋垂荡抑制结构的圆筒型FPSO,并通过模型实验研究了垂荡抑制结构对运动性能的影响,结果表明两者均起到了增加阻尼的作用,而带外板边锋垂荡抑制结构的阻尼增加效果最显著。
本文基于CFD 的方法对带减动结构的圆筒型FPSO 进行数值模拟,建立三维数值水池模型,进行网格无关性和时间步长稳定性验证,通过用户自定义函数(User Defined Function,UDF)模拟FPSO发生强迫垂荡运动的方式计算得到垂荡阻尼和附加质量,进而探究不同运动周期和幅值下的圆筒型FPSO 的垂荡阻尼和附加质量变化规律。
1 理论方法
本文基于CFD 方法,采用Fluent 软件进行数值模拟,本节简要介绍了流体基本控制方程、流体体积法、湍流模型和阻尼、附加质量的计算方法等内容。
1.1 基本控制方程
流体的连续方程和动量方程共同组成了流体运动的基本控制方程(Navier-Stokes 方程),即N-S方程。考虑非定常、不可压缩流体,方程可写为如下分量形式。
式中,u、v、w分别为x、y、z方向上的速度分量;ρ为流体的密度;p为流体微元所受的压力;v为流体运动黏滞系数。
对于大多数流动问题而言,体积力一般为重力,则有gx=gy=0 和gz=-g。其中,g 为重力加速度。
1.2 流体体积法
海洋结构物数值模拟通常涉及两相流问题,Fluent 中解决两相流问题的典型方法是流体体积(Volume of Fraction,VOF)法,即通过计算单个网格单元内流体体积与网格体积的比值,从而确定自由液面的位置和形状,该方法简单易行、收敛精度高且稳定性好。
若某流动问题涉及n相流体,单个网格单元中第i相流体体积分数为qi,则有0≤qi≤1,且流体总的体积分数须满足式(5)。
对于两相流而言,若想确定自由液面的位置,只需追踪qi=0.5 的所有网格单元即可。
1.3 湍流模型
湍流的数值模拟方法中,大涡模拟(Large Eddy Simulation,LES)将大于网格尺寸的湍流涡运动通过控制方程直接得到,再建立近似模型模拟小尺度涡对大尺度涡运动的影响,该方法计算资源消耗大但精度高。Reynolds 平均法(Reynolds-Averaged Navier-Stokes,RANS)对瞬态N-S 方程进行时间平均处理,并且补充反映其特性的湍流输运方程,其消耗的资源和时间均少于LES,也是目前采用最多的方法。此外还有RANS/LES 混合方法,兼具了RANS 计算量小和LES 精度高的特点。本文采用RANS 中的SSTk-ω模型,其由Menter 提出,考虑了逆压梯度边界层的主要剪切应力输运,可用于逆压力梯度流动,广泛用于黏性模拟,适合一般流动和内部流动等问题。
其输运方程为如下。
式中,Γk和Γω均为代系数;μt为湍流粘度,且有。Gk和Gω来自湍流项,表示为。Yk和Yω是湍流耗散项。
1.4 用户自定义函数(UDF)
UDF 是用户利用C 语言编写的函数,可以被Fluent 动态加载。用户可以通过UDF 来定义边界条件,设置材料性质,定义输运方程中的源项,定义初值等。其作为一个辅助工具在Fluent 数值模拟中应用十分广泛。本文使用UDF 实现结构的强迫垂荡运动,调用DEFINE_CG_MOTION 宏,定义结构垂荡方向的速度,赋予初值,从而模拟结构强迫垂荡运动。
1.5 垂荡阻尼和附加质量计算
若给定浮体强迫垂荡运动的形式为简谐运动ξ3=Asinωt,则浮体所受水动力可表示如下。
式中,A为垂荡幅值;ω为运动频率;F0为受力幅值;φ为相位差。将运动和受力方程整理得到式(9)[4]。
浮体仅发生垂荡运动,垂荡方向满足力平衡方程。
联并式(9)和式(10),有
式中,c为浮体的阻尼系数;m为附加质量;φ为相位差。
本文通过CFD 计算可得到垂荡方向的水动力时历曲线,进而得到受力幅值F0和相位差φ,代入式(11)计算得到垂荡阻尼系数c和附加质量m。该方法也适用于通过强迫运动形式计算结构的摇荡阻尼,原理类似。
1.6 无量纲附加质量和无量纲阻尼系数
无量纲附加质量和无量纲阻尼系数是反映结构水动力性能的重要参数。为了探究两者在不同运动参数下的变化规律,根据文献[10]中的方法可计算得到上述参数,如式(12)和式(13)所示。
式中,Cd为无量纲阻尼系数;Ca为无量纲附加质量系数;S为投影面积;为结构排水体积。
2 圆筒型FPSO 数值建模及验证
2.1 FPSO 主尺度参数
圆筒型FPSO 的模型如图1 所示,主筒体的下部为延伸筒体,围绕延伸筒体周围设置有减动结构,能增加结构垂荡运动时的附加质量和阻尼,从而削减结构运动响应。圆筒型FPSO 的几何主尺度参数如表1 所示。

表1 圆筒型FPSO 几何参数
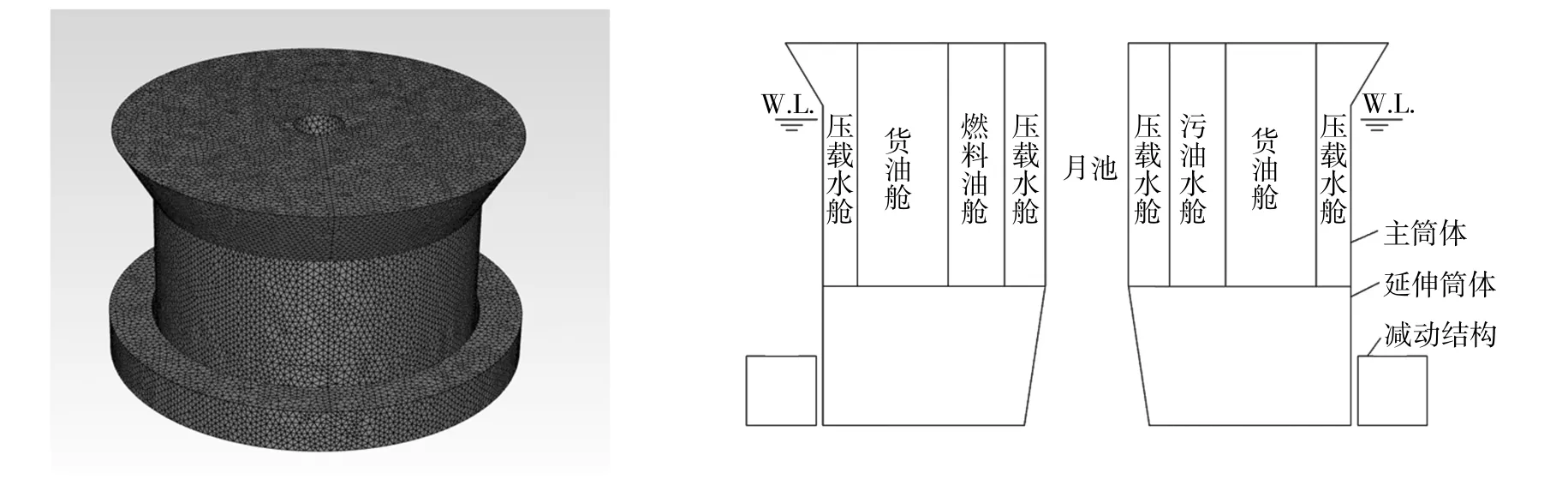
图1 圆筒型FPSO 模型
2.2 网格无关性验证
本文采用Fluent 软件进行CFD 仿真计算,建立的计算域大小为500 m ×800 m ×380 m,在结构周围划分加密网格,且通过UDF 使得结构发生给定周期和幅值的强迫垂荡运动,实时输出垂荡方向的力Fz。边界条件是左侧为压力入口,右侧压力出口,四周为对称边界条件,FPSO 设置为无滑移壁面条件,如图2 所示。
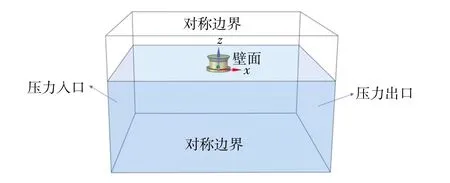
图2 边界条件示意图
为了验证网格尺寸对于计算结果的影响,通过控制网格疏密程度生成了三种网格方案,选取结构垂荡运动周期为5 s,幅值为1 m 的工况,对比的计算结果如图3 所示。
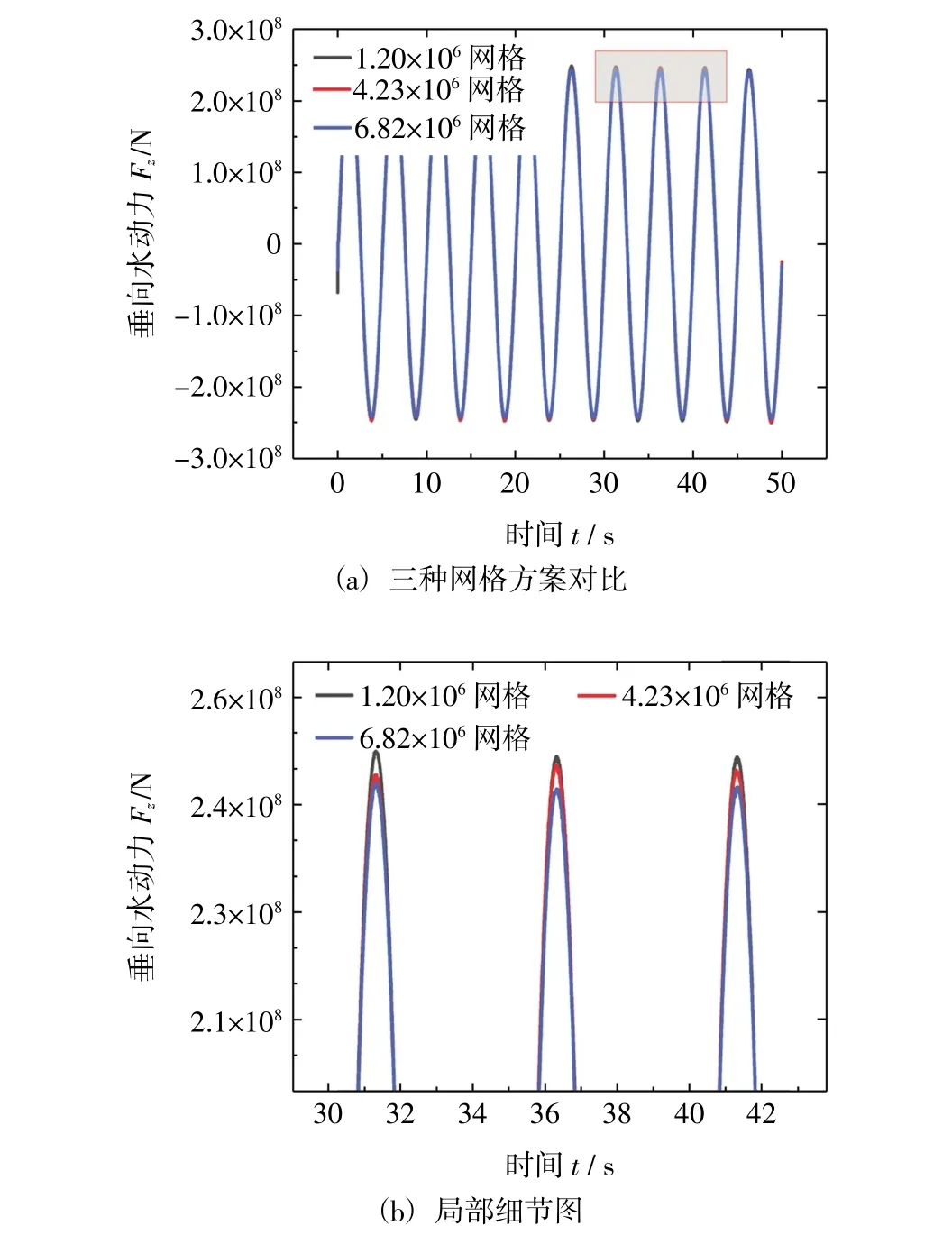
图3 网格无关性验证
通过式(12)和式(13)算得无量纲阻尼和附加质量系数结果如表2 所示,随着网格数量增加,参数结果差异维持在5%以内,可认为网格已趋于收敛,后续计算选用423 万网格。

表2 三种网格方案下无量纲阻尼和附加质量对比结果
2.3 时间步长稳定性验证
为了探究不同时间步长的选取对于无量纲附加质量和阻尼系数的影响,选取时间步长为0.01 s,0.015 s 和0.02 s 三种工况,进行时间步长稳定性验证。强迫垂荡运动周期为20 s,幅值为2.4 m,CFD输出的垂向水动力结果如图4 所示。
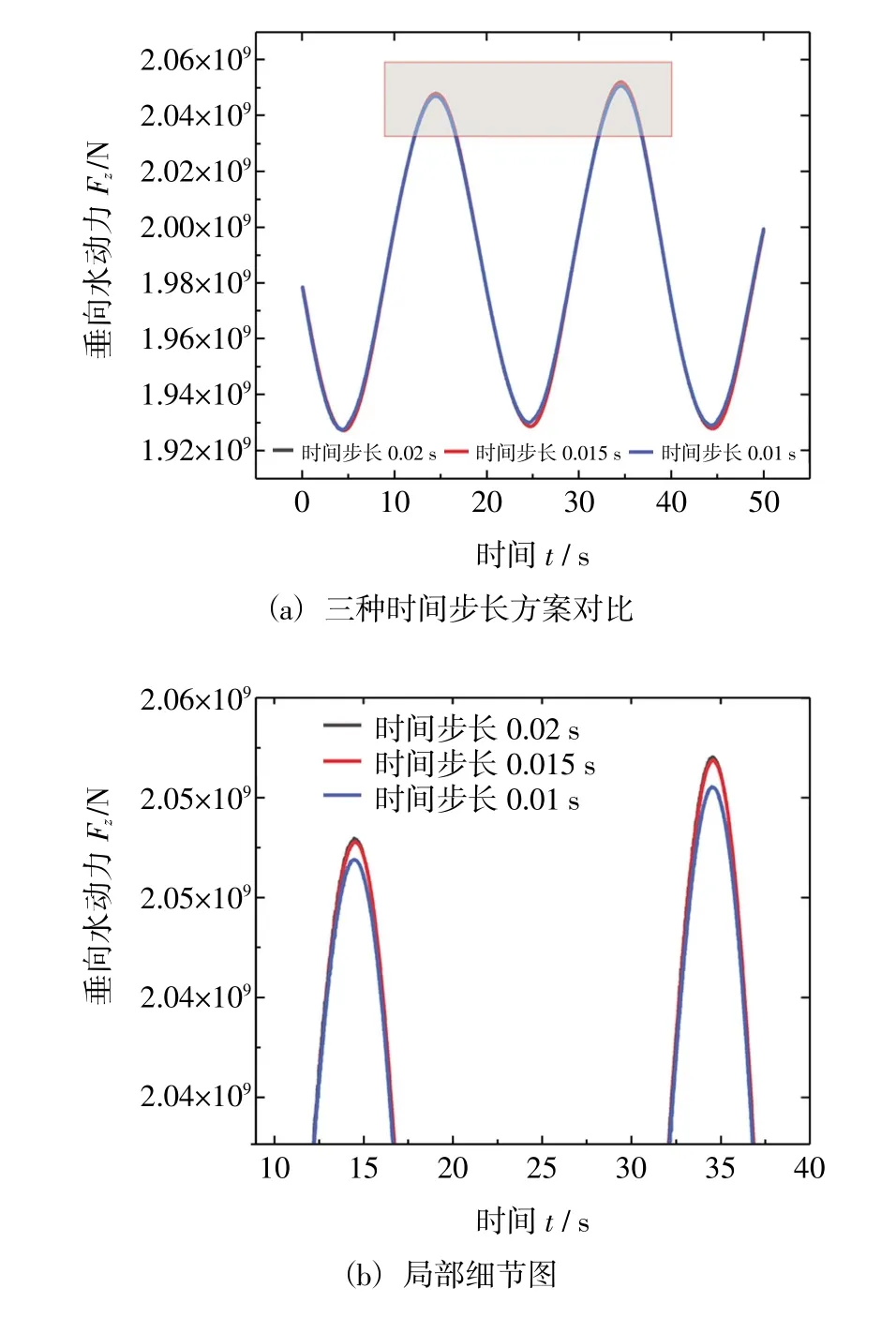
图4 时间步长稳定性验证
无量纲阻尼和附加质量系数的结果列举在表3中。可见,随着时间步长缩短,计算结果的差异保持在5%以内,且有减小的趋势,后续计算选用0.02 s 的时间步长。
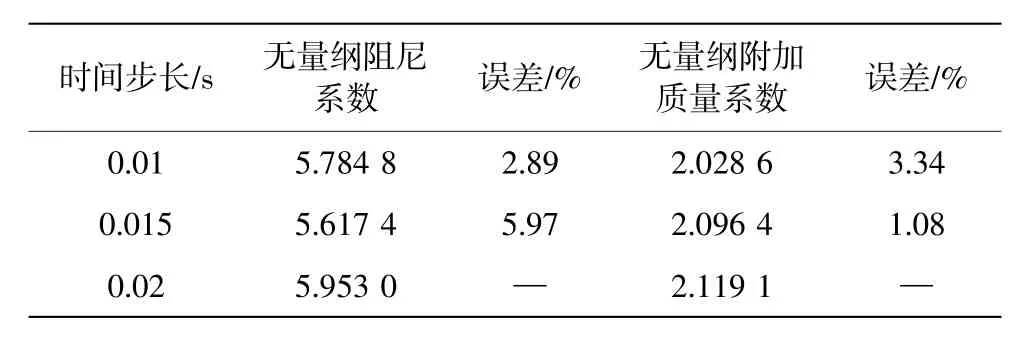
表3 三种时间步长方案下无量纲阻尼和附加质量对比结果
3 计算结果及分析
基于建立的三维数值水池模型,通过软件Fluent 的用户自定义函数UDF 模拟圆筒型FPSO 强迫垂荡运动,运动的周期和幅值通过UDF 编译设定,输出垂荡方向水动力的时历曲线,拟合后根据式(11)计算得到垂荡阻尼系数和附加质量。为了探究圆筒型FPSO 在不同的垂荡周期和幅值下的阻尼系数和附加质量变化规律,本文选取了工程中典型的垂荡运动周期和幅值范围,通过Fluent 数值模拟分别计算得到结果如表4 和表5 所示。
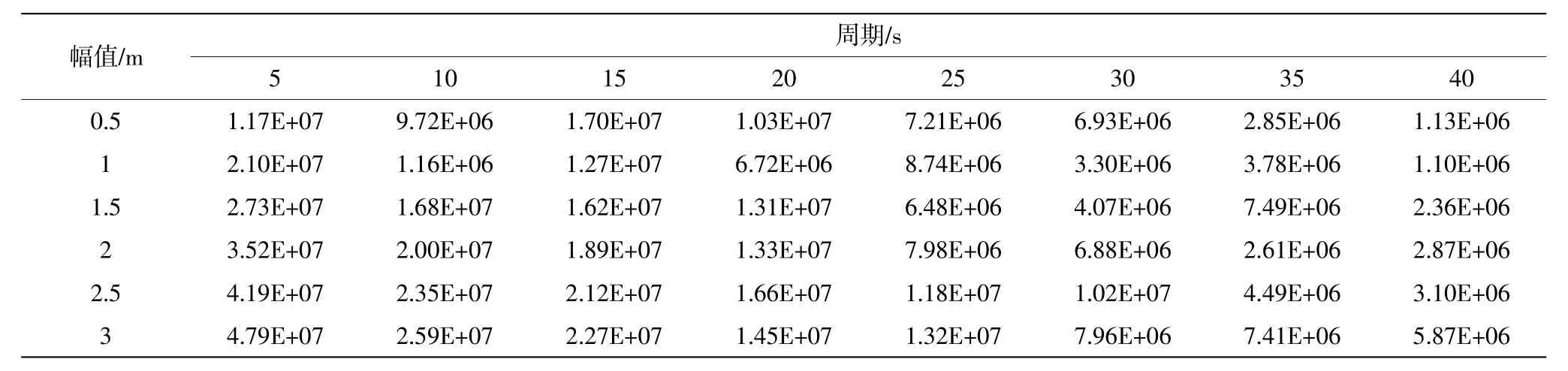
表4 不同垂荡周期和幅值下的垂荡阻尼系数 单位:N·s·m-1

表5 不同垂荡周期和幅值下的附加质量 单位:kg
图5 直观地展示了垂荡阻尼系数和附加质量与垂荡运动周期和幅值的关系。可以发现,随着垂荡运动周期的增大,垂荡阻尼系数以较快的速度减小,而垂荡附加质量在缓速减小后急剧上升。且垂荡运动周期越大,垂荡阻尼系数受垂荡运动幅值的影响越小。当垂荡运动周期接近垂荡固有周期时,垂荡附加质量出现极小值。
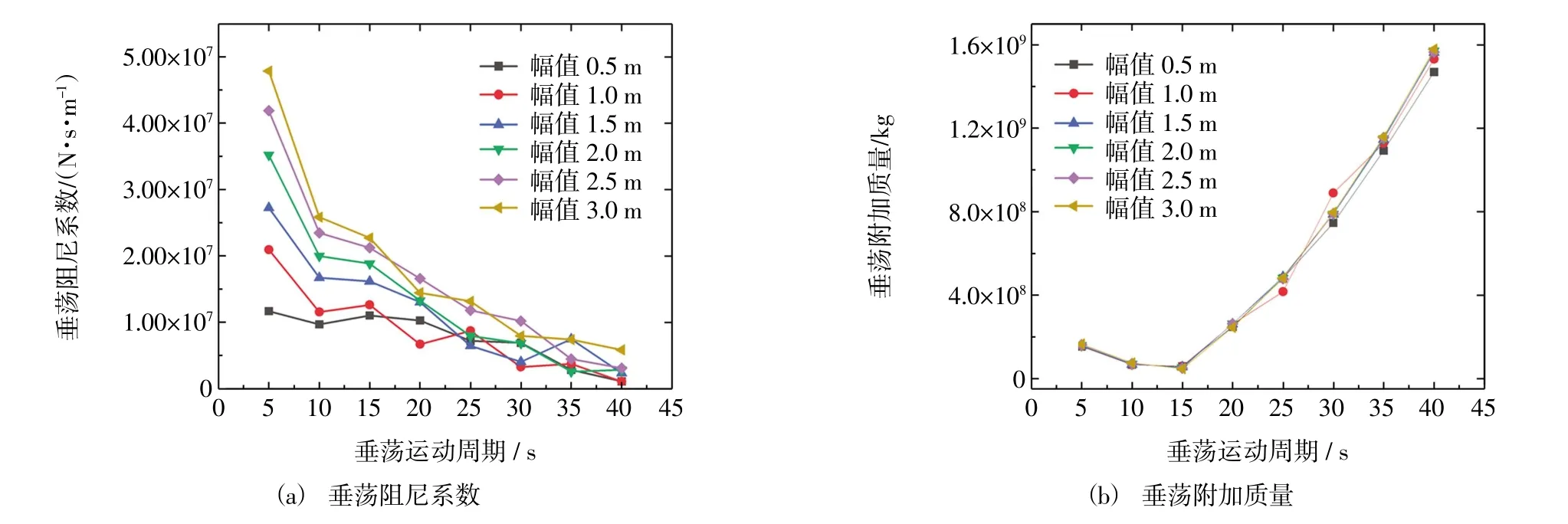
图5 不同周期和幅值下的垂荡附加质量和阻尼系数
实际海况中,波浪周期接近结构垂荡固有周期时,会激起较大的垂荡运动响应。为了探究垂荡附加质量和阻尼系数随垂荡运动幅值的变化关系,取垂荡运动周期为15 s 时垂荡附加质量和阻尼系数结果进行对比,如图6 所示。垂荡运动周期接近垂荡固有周期时,垂荡阻尼系数与垂荡运动幅值线性正相关,而垂荡附加质量呈负相关关系。
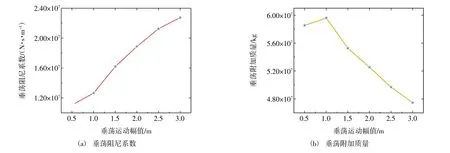
图6 不同运动幅值下的垂荡附加质量和阻尼系数(运动周期为15 s)
在表4 和表5 结果的基础上,为了进一步分析圆筒型FPSO 水动力特征,由式(12)和式(13)计算得到圆筒型FPSO 在不同垂荡运动周期和幅值下的无量纲阻尼系数和无量纲附加质量系数,结果如表6 和表7 所示。
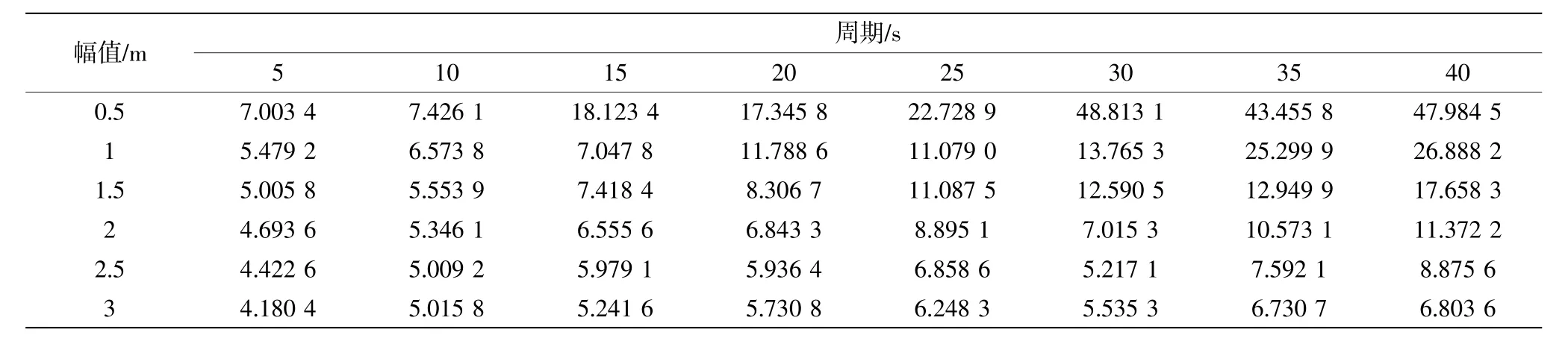
表6 不同垂荡周期和幅值下的无量纲阻尼
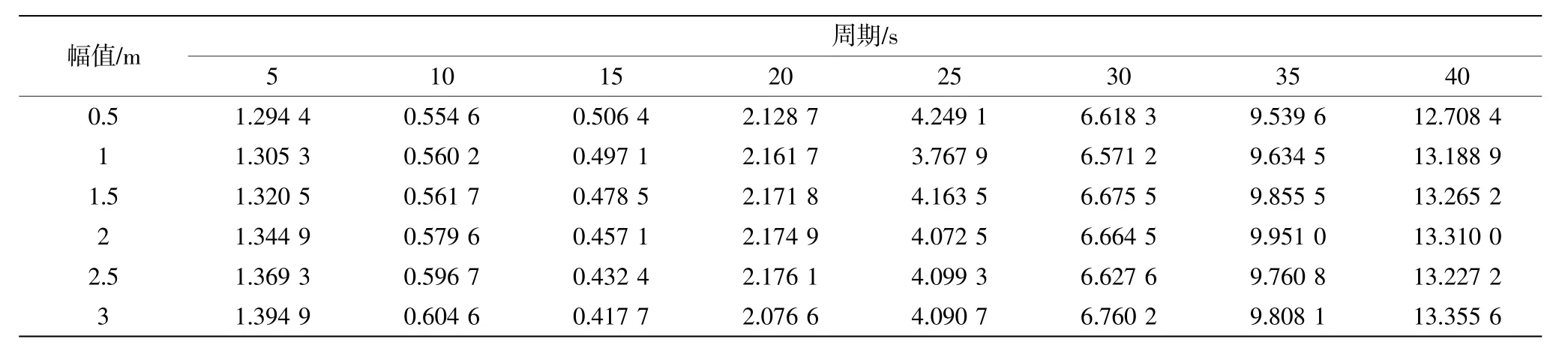
表7 不同垂荡周期和幅值下的无量纲附加质量
图7 中展示了无量纲阻尼和附加质量系数随垂荡运动周期和幅值的变化规律。结果可知,随着垂荡运动周期的增大,无量纲阻尼系数整体呈现出增长的趋势,这与垂荡阻尼的趋势是恰恰相反的。垂荡运动周期较大时,无量纲阻尼系数对垂荡运动幅值较敏感。而无量纲附加质量系数的变化规律与图5(b)中所展示的规律并无大异,且几乎不受垂荡幅值的影响。

图7 不同运动周期和幅值下的无量纲附加质量和阻尼系数
如图8 所示,当垂荡运动周期接近结构垂荡固有周期时,无量纲附加质量和阻尼系数均与垂荡运动幅值负相关。其中,垂荡运动幅值较小时(小于1.0 m),无量纲阻尼系数骤降;垂荡运动幅值达增大到一定值时(大于1.0 m 且小于3.0 m),无量纲阻尼系数缓速减小。
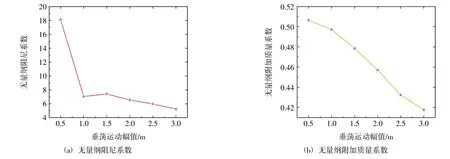
图8 不同运动幅值下的无量纲附加质量和阻尼系数(周期为15 s)
4 结 论
本文利用CFD 对带减动结构的圆筒型FPSO 进行了数值模拟,通过模拟结构强迫垂荡运动,输出垂向体积力,计算得到不同运动参数下的垂荡阻尼系数和附加质量,得出以下研究结论。
(1)对于圆筒型FPSO,垂荡阻尼系数与垂荡运动周期负相关,与垂荡运动幅值呈线性正相关,且垂荡运动周期较小时,垂荡阻尼系数受垂荡运动幅值的影响较明显。
(2)垂荡附加质量随着垂荡运动周期增大呈现明显上升趋势,但其对垂荡运动幅值不敏感。垂荡运动周期接近垂荡固有周期时,垂荡附加质量出现极小值。
(3) 随着圆筒型FPSO 的垂荡运动周期增大,无量纲阻尼系数受垂荡运动幅值的影响愈明显。具体表现为:无量纲阻尼系数随着垂荡运动幅值增大而逐渐减小。
本文研究结果可为圆筒型FPSO 在工程中的应用提供一定参考。然而,本文是采用CFD 的方法计算圆筒型FPSO 的垂荡阻尼,计算的垂荡运动周期区间较稀疏,运动幅值范围并不能涵盖工程典型海况。此外,垂荡抑制结构通海能较大程度上改善圆筒型FPSO 的垂荡性能[11],利用CFD 的方法探究运动抑制结构通海对于垂荡性能的改善效果也是一个值得尝试的思路。
