基于Dijkstra 算法下本溪市旅游路线与最大旅游收入的研究
2024-01-13李芳芳甘向前赵鑫宇
张 宇,李芳芳,甘向前,赵鑫宇, 姜 雄
(1.辽宁科技学院基础部,辽宁 本溪 117004;2.辽宁科技学院电气与自动化工程学院,辽宁 本溪 117004)
旅游线路是旅游者的重要攻略, 区域旅游收入与旅游者设计线路有着必然的联系。 如何在旅游规划中,使旅游者和旅游产业获得双赢,是旅游经济的重要课题。文章通过对辽宁本溪地区旅游业的分析,结合相关数据和旅游线路, 探索本溪地区旅游产业的发展,为旅游产业的发展提供参考[1-3]。
1 本溪旅游线路的研究
1.1 背景研究
随着科技的发展、社会的进步,人们对生活质量的要求显著提高。伴随着物质需求的提高,精神生活的追求也随之提高[4]。 因此,越来越多的人选择了旅游,促使旅游业成了我国的一个支柱产业。如何提高旅游效率, 如何保证游客在最短的时间内体验到最优质的旅游体验, 这些都是本溪市旅游业的当务之急[5],也是文章关注的重点。 因此,在满足旅游需求约束条件下, 如何让游客花最少的钱游览尽可能多的景点,是本文的研究重点。
1.2 本溪市旅游景点信息
本溪市旅游景点的相关信息(景点名称、景区等级、营业时间、门票价格等)如图1 所示。 其中,每个景点的等级、营业时间和门票价格均已标注。 此外,与图1 对应的各个景点之间的距离如表1 所示。
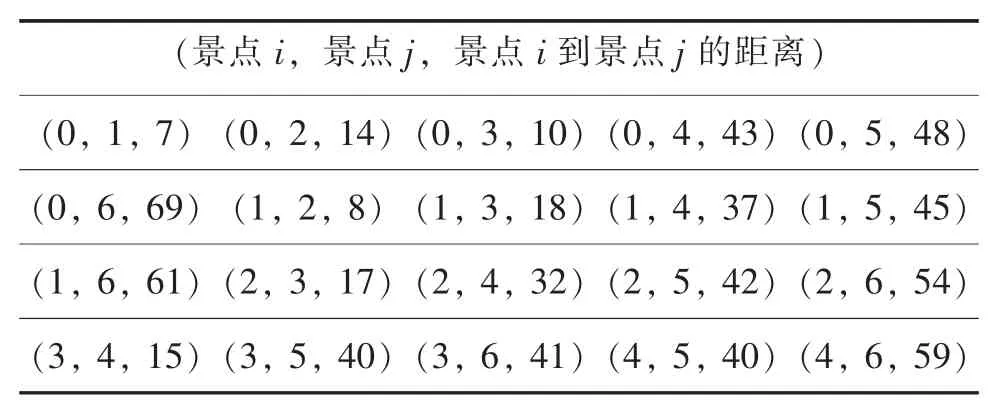
表1 景点i 与景点j 之间距离/km
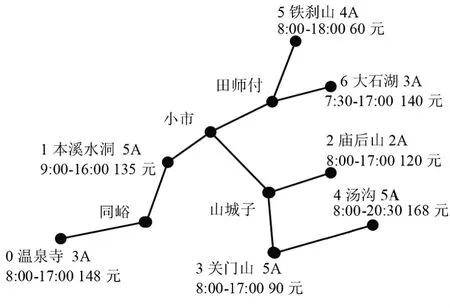
图1 本溪市旅游景点示意图
1.3 模型假设条件
假设1,旅客在去往旅游景点的旅途中,车速恒定,且忽略突发事件干扰。
假设2,两地距离接近于两地的直线距离。
假设3,各景区严格遵守营业时间。
1.4 输入说明
在程序的第1 行,输入4 个正整数(N、M、S 和D),具体如下:
a. N (2≤N≤500)是旅游景点的个数,并且旅游景点的编号从0 到(N-1),总共N 个整数;
b. M 是公路的条数;
c. S 是第一个景点编号;
d. D 是最后一个景点编号。
随后的M 行中,每行给出一条公路的信息(景点1、景点2、公路长度、景点2 门票价格)。 其中,信息之间用空格隔开,数字均为整数且不超过500。 输入的过程中,确保解的存在。根据本溪市旅游景点地图,确定旅游景点的具体位置和相关距离,把每个景点编成序号(0,1,2,……),利用两个景点的直线距离代表公路距离,将最早营业的景点设为第一个,最晚结束的景点设为最后一个, 利用C 语言软件编程进行实验,得到最优解。
1.5 模型介绍
本文选择Dijkstra 算法。
(1)算法特点:
Dijkstra 算法就是利用广度优先搜索解决赋权有向图或者无向图的单源最短路径问题, 最终得到一个最短路径树。 该算法常用于路由算法或者作为其他图算法的一个子模块。
(2)算法思路:
Dijkstra 算法采用一种贪心策略,声明一个数组dis 来保存原点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合T,初始时,原点s 的路径权重被赋为0 (dis[s]=0)。 若对于顶点s 存在能直接到达的边(s, m),则把dis[m]设为w (s,m),同时把所有其他(s 不能直接到达的)顶点的路径长度设为无穷大。 初始时,集合T 只有顶点s。
然后,从dis 数组选择最小值,则该值就是原点s 到该值对应的顶点的最短路径,并且把该点加入T中,此时完成一个顶点。
接着, 判断新加入的顶点是否可以到达其他顶点, 并分析出通过该顶点到达其他顶点的路径长度是否比原点直接到达的路程短。如果找到最短路径,则用最短路径替换顶点在dis 中的值。
重复上述步骤, 直到T 中包含了图1 中所有顶点。
1.6 仿真结果
第一天从最早营业的大石湖旅游景区出发,到最晚结束营业的汤沟景区,途径关门山景区,该行程距离最短为56 km,花费180 元。
第二天从汤沟景区到庙后山景区, 途径水洞景区,该行程为45 km,花费270 元。
第三天从庙后山景区到铁刹山景区, 途径温泉寺景区,该行程为90 km,花费208 元。
2 关于本溪旅游风景区的最大收入研究
2.1 现代旅游业的形势
当今中国,全国经济开始迅速增长,我国社会的主要矛盾已转化为人民日益增长的美好生活需要和不平衡不充分的发展之间的矛盾。其中,人民对旅游的需求越来越高,随之而来的是旅游业的蓬勃发展。但受疫情影响,旅游业受到一定冲击。 因此,在危机之下,研究转型发展成了必然趋势。
2.2 本溪旅游业现状
作为旅游城市, 本溪市因位于辽东丘陵与长白山脉之间的特殊地带,形成了独特的风景区,例如,本溪水洞(5A 级)、五女山景区(4A 级),以及关门山森林公园等。
受到新冠疫情冲击,经济发展放缓,旅游业同样受到冲击。相关研究表明,本溪市旅游业跟往年同期相比,游客人数比例下降了30.23%,旅游收入也下降了32.51%。 此外,相关产业结构并没有随着疫情突然来临而及时调整, 造成了目前旅游业发展的停滞不前。
2.3 具体分析旅游业实际情况
本溪森林公园在本溪旅游业中占比92%。 因此, 文章以本溪森林公园为主要的数学模型进行模拟,在2018-2020 年期间,本溪国家森林公园的具体收入支出占比见表2。
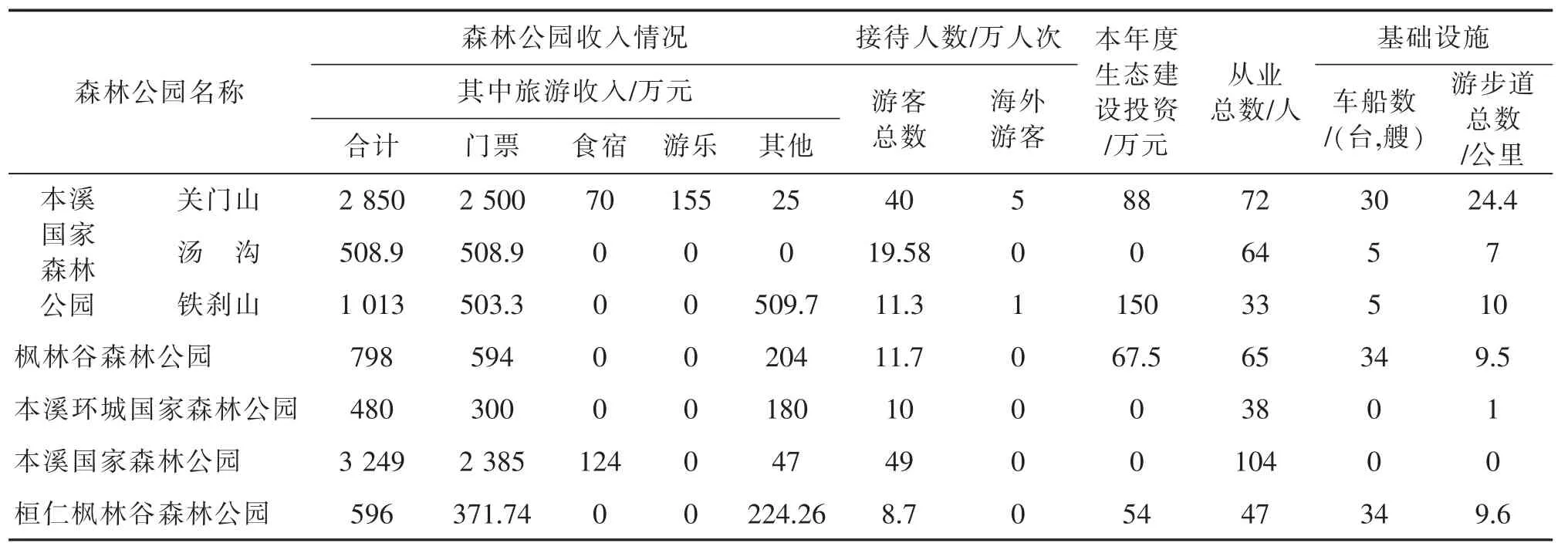
表2 本溪森林景点的相关信息
因此,若要研究旅游景点的收入,需要研究景点的旅游人数。 而和旅游人数相关的变量则包括建设投资、职工总数、车辆总数和游客步道公里总数。
此外,还需判断这些变量是否与旅游人数相关。本文使用SPSS 进行偏相关分析,结果如表3-表6所示:
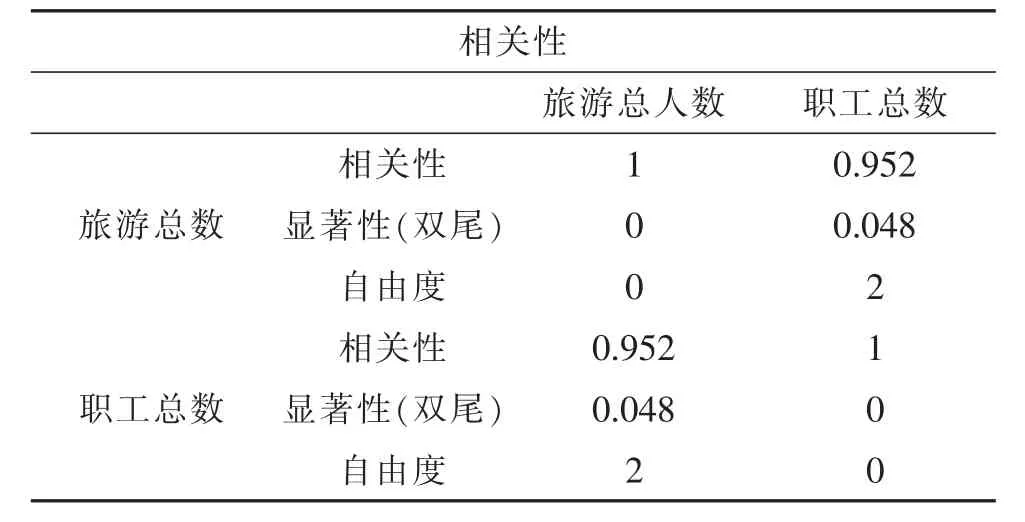
表3 相关性1(控制:生态建设投入& 车船总数& 旅游步道总公里数)
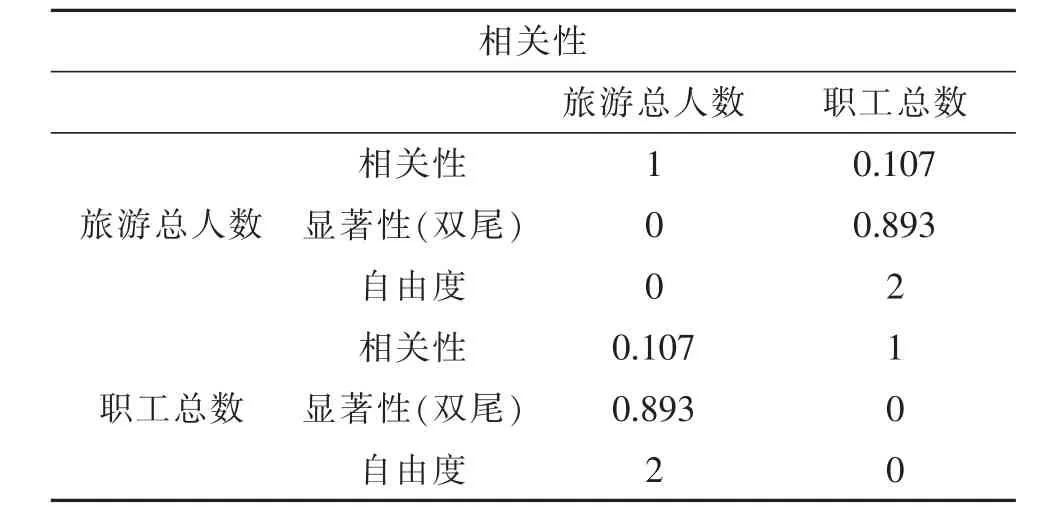
表4 相关性2(控制:车船总数& 旅游步道总公里数& 职工总数)
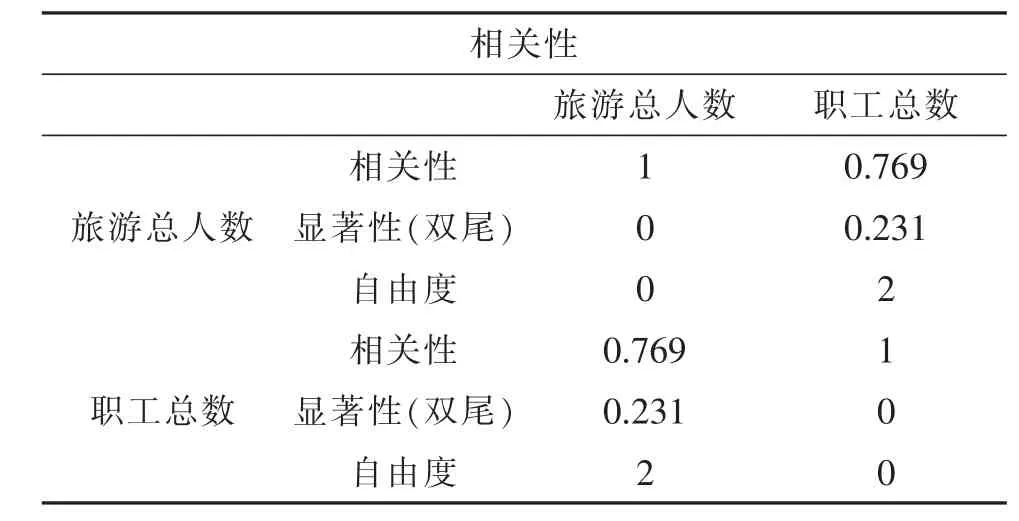
表5 相关性3(控制:车船总数& 职工总数& 生态建设投入)
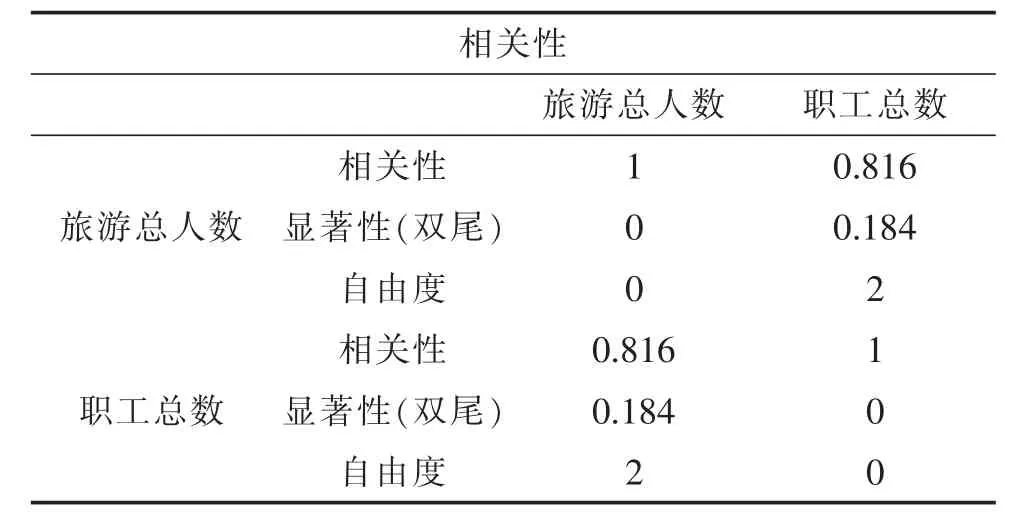
表6 相关性4(控制:职工总数& 生态建设投入& 旅游步道总公里数)
对表2 数据进行分析。表2 表明,门票收入是旅游景点的主要收入来源,如公式(1)
当显著性低于0.05 时,表示旅游人数和该变量相关,也表明“旅游人数—变量”函数关系具备研究价值。
相关研究表明, 旅游人数与职工总数之间存在关系。因此,文章以旅游人数为因变量y,职工总数为自变量x,使用MATLAB 对数据做拟合曲线的处理,结果如图2 所示。
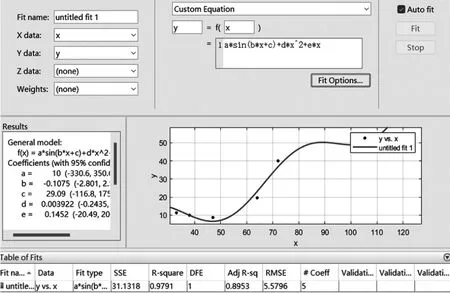
图2 MATLAB 拟合结果
该函数为:
由于
SSE: 31.13
R-square: 0.9791
Adjusted R-square: 0.8953
RMSE: 5.58 删除
图2 表明,公式(2)高度符合真实数据。 但理论数据仅考虑了理想状态。 实际情况中,职工总数并不是一个固定值,而是随着旅游人数变化而改变。并且,旅游人数并不会随着职工人数增加而增多。
研究表明, 景区的旅游收入并不会因为景区方职工总数、车船量、生态建设投资、客步道公里总数的变化而变化。 景区想要增加旅游收入,必须进行体制改革,寻求改变,不能单一地依靠门票收入。
3 本溪旅游业面临的问题以及未来方向
疫情的影响下,传统旅游业出现了诸多的问题,例如,相关产业不完整,周边经济发展不平衡,产业部署不均衡,没有带动区域经济的整体发展等,具体内容如下。
3.1 旅游业面临的问题
传统旅游业的主要收入为门票收入。 但面对游客骤减的情况, 门票收入则显现出脆弱的抗风险能力。 因此,只有主动求变,才能摆脱对单一门票经济的过度依赖,扩展景区特有景观的影响力,从而衍生出不同于传统旅游业的经济产业链。此外,旅游业的发展也能带动周边经济的共同发展。 作为吸引游客的黏合剂, 旅游业与本地诸多其他产业形成有效联动,不仅可以增强行业的抗风险能力,还可以促进其他产业的发展。 此外,旅游业与其他产业相结合,会共同创造价值。挖掘周边特有的经济潜力,特别是开发当地特有的民俗文化。结合实际情况,建设富有文化底蕴的旅游胜地,形成独具特色的风景名胜。
3.2 本溪旅游业未来方向
为了应对疫情等相关突发事件的冲击, 可使用科学技术的手段提升旅游业精细化管理程度, 使得“无预约,不旅游”成为社会常态。
同时,通过有效使用大数据等信息,实现对景区游客的精准控制、分流,并有效提高相关管理部门的管理服务效能,促进对传统旅游业的转型发展。
此外,借助数字化的精细管理,景区可以更加高效地了解游客,并提出富有建设性的建议,提升游客体验,增加游客的满意度,从而留住游客。
再有, 发展更加便捷的交通, 增加人性化的服务, 提高知名度。 逐步实现当地的旅游业与现实情况深度结合,形成一个完善的有机经济整体。
最后, 本溪地区风景区旅游资源丰富, 种类多样, 特色鲜明。 如何实现本溪旅游文化的飞速发展是一个长久的课题,通过本研究,为本溪地区的旅游经济发展提供一种思路,希望在未来,本溪的旅游业更加辉煌。
4 结语
针对本溪地区旅游产业的发展, 以及对旅游线路、旅游模式、旅游营销等各种方式的研究,对本溪地区的经济统筹发展具有重要意义。 文章基于旅游景点的真实数据,运用优化模型Dijkstra 算法,构建最优化的旅游空间线路, 并且对不同的空间线路进行对比分析,得出最适合本溪地区发展的旅游模式。并且在这种情况下,运用MATLAB 预测出本溪地区的旅游收入的最大资源。 这种研究方法填补了旅游经济的一项空白,不仅仅对本溪地区,甚至对全国旅游经济链的运行和发展方式都有着重要的意义。
