基于Euler-Euler 方法的VD 炉脱气过程数值模拟
2024-01-13张慧书
余 珊,张慧书,孙 野,陈 韧
(1.辽宁科技学院冶金与材料工程学院,辽宁 本溪 117004;2.辽宁省低品位非伴生铁矿优化应用重点实验室,辽宁 本溪 117004)
0 引言
众所周知,现代炼钢生产中,为去除钢水中的气体杂质,通常采用搅拌和真空操作:一方面,通过气体搅拌引导钢液循环流动, 从而强化熔池内质量和能量传递,有效缩短处理周期,同时熔池内因底部吹气体形成的气液混合区(或称羽流区)还能极大增加气液接触面积, 为相关冶金反应提供良好的动力学条件; 另一方面, 则是利用真空环境降低目标气体(氢气/氮气)在气相中的分压,从而破坏其在钢中的溶解平衡,最终达到将其脱除之目的[1-3]。一般地,冶金中的真空(脱气)装置有两类,一类涉及真空循环,如RH 精炼, 具体是利用气体做功产生钢水和钢包与真空室之间的循环流动, 从而在真空室中实现各种复杂的物理化学反应;另一类为真空底吹,如VD精炼, 具体是通过多孔塞向置于真空室内的钢包底部喷吹惰性(一般为氩气)气体促进钢水循环并达到脱气效果。 这两种真空装置均有广泛的应用, 而其中,VD 精炼炉设备简单,吹氩搅拌效果好,渣、钢反应活跃,投资和生产运行成本相对低廉,将其与LF炉联合,便能以较低成本生产中高碳以及对H、S、N等有害元素含量要求苛刻的钢种。 文章基于Euler-Euler 方法,建立了可用于描述真空条件下反应器内气液流动和传质行为的通用计算流体力学(CFD)模型。 为展示其应用效果,还将该CFD 模型用于某钢厂在产(100 t)VD 精炼炉,所得预测结果与现场实测数据吻合度高, 表明模型可用于进行VD 精炼过程的相关应用基础研究。
1 模型介绍
1.1 主要假设及简化
本文CFD 模型主要用于研究真空条件下反应器内的气液流动和传质行为, 其主要假设及简化如下:
(1)模型仅考虑气相和液相,不考虑钢渣对钢水流动的影响;
(2)考虑一般VD 操作导致的钢水温降较低,模型忽略温度的影响;
(3)脱气反应只发生在羽流区以及钢液面裸露区域(即渣眼),其中,渣眼的大小由工厂实测数据给定。
1.2 控制方程
为节省篇幅, 以下仅给出模型所涉及控制方程的具体表达式,其中更多细节的相关参数/系数可参见文献[4]和[5]。
模型的连续性方程为:
其中,α、ρ 和u 分别为体积分数、 密度和速度矢量;下标q 代表气相(g)或液相(l)。
任一相的动量守恒方程为
其中,P、μeff以及g 分别为压力、 有效黏度以及重力加速度;下标q 代表任一相,则p 就代表另一相。分别为升力和曳力。
为合理描述气体底吹系统中的湍流现象, 文章模型求解如下的修正k-ε 湍流方程[3-9]。
式中, 下标mix 表示混合相;μt和Gk分别为湍流黏度和湍动能生成项;Sk和Sε分别为k 方程和ε 方程的源相,二者的表达式分别为。
为获得气液相界面浓度分布, 本模型计算如下方程[10-13]。
其中,SRC、SWE和STI分别为由随机碰撞引起的气泡聚合项, 夹带引起的气泡聚合项以及湍流导致的气泡破碎项。
为获得钢水中各组分的浓度分布, 模型求解如下组分输运方程。
其中,下标i 可为[X]或X2(即溶解态或气态的氢或氮组分);Yi,q和Ji,q分别为组分的质量分数和扩散通量;Si,q为源相并满足S[X],1=-SX2,g,即单位时间单位体积中液相中反应掉的反应物[X]的质量恒等于气相中生成的产物气体X2。
1.3 边界条件及其他
对于液相而言, 模型计算域中的自由上界面为无滑移边界,但对气相而言,其为可穿透边界,也就是所谓的“脱气边界”。为实现该边界,本文模型通过向与自由上界面相邻的计算单元的气相守恒方程中加入以下源相。
其中,wg、Afs和Vcv分别为垂直于自由上界面的气相分速度、 计算单元包含的自由上界面面积以及相邻计算单元的体积。
本模型中,各壁面对液相为无滑移边界,对气相则为滑移边界, 对所有近壁面处湍流变量应用标准壁面函数处理。 熔池中气泡的静压Pb为
其中,Pv和h 分别为真空压力和所在计算单元(几何中心)距自由上界面的距离。
2 某厂实际VD 炉
为展示上述CFD 模型的应用效果,文章将其用于研究某钢厂在产(100 t)VD 精炼炉内的钢水流动和脱氢脱氮(统称脱气)行为。 所述VD 精炼炉的尺寸以及吹氩和真空操作制度分别见图1 和图2。
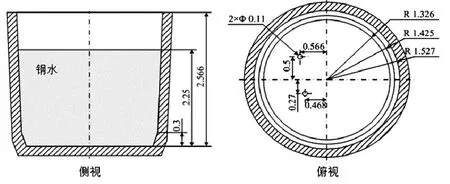
图1 某厂(100 t)VD 精炼炉主要几何尺寸(单位:m)
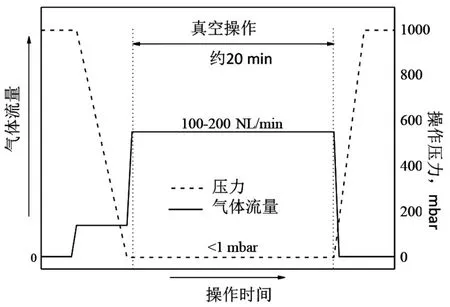
图2 某厂VD 精炼炉吹氩和真空操作制度
由图1 可知,该VD 炉内壁略有倾角,最小内径为2.652 m,最大内径为3.054 m,熔池(钢水)深度为2.566 m(对应质量约100 t)。 氩气通过两个多孔塞吹入溶池, 多孔塞位置安排见图1 中的右图。 通过两个多孔塞的气体流量相等, 且总流量随处理时间变化如图2 所示。 可以看到,氩气流量在初期为阶梯式递增, 主要目的是防止抽真空降压过程中气体体积膨胀过快造成的急剧熔化泡沫渣。 当压力达到最低值的同时,气体流量增大到目标值(约为0.1 Nm3/min~0.2 Nm3/min)。 操作压力一般低于1 mbar,并持续20 min。
该厂VD 精炼炉主要用于钢水的脱氢和脱氮,目标产品为管线钢。随着冶金技术发展,其他杂质元素如氧、 硫、 氢等的含量均已能够脱除到很低的程度,例如,目前的操作制度已经可以较容易地将钢水中氢的浓度控制在1 ppm 以下。 但是,氮的原子半径比氢大,在钢中的扩散系数比氢小两个数量级,使得脱氮并不像脱氢那样容易。另外,氮不像氧那么活性高,能与强脱氧剂铝形成夹杂并通过上浮去除。实际上, 钢水中的氮与大多数合金元素形成的氮化物在高温下会分解,故无法通过上浮去除[14]。 因此,该厂对钢水中气体杂质含量的要求一般为氢含量不高于1 ppm,氮含量不高于30 ppm。表1 为该厂VD 精炼前的典型钢水成分,可以看到,钢水在二次精炼前的碳含量在0.10%到0.35%之间, 而其中氧含量则更是低于6 ppm, 这说明精炼过程中几乎不发生脱碳反应。
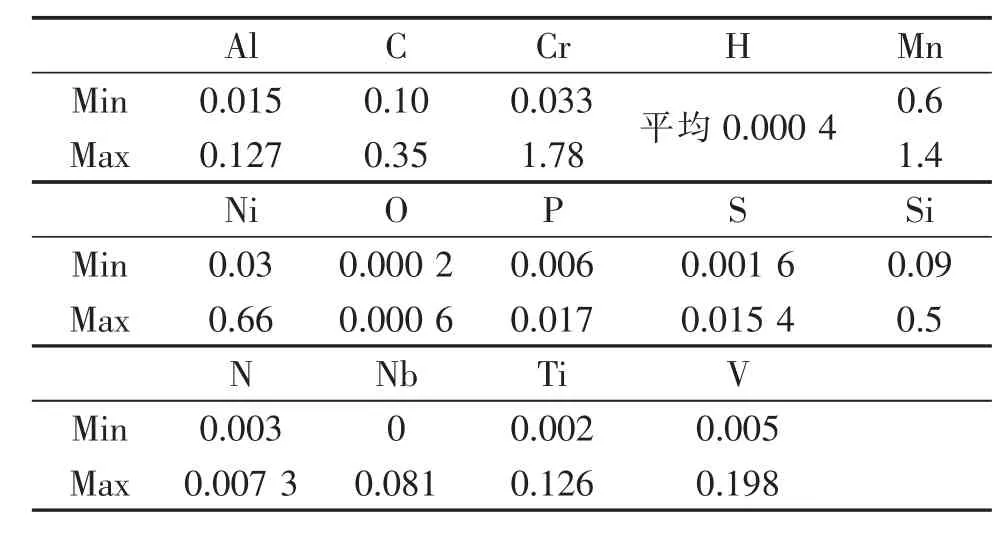
表1 某厂VD 精炼前的典型钢水成分/wt%
3 模型应用效果
图3 为总氩气流量0.13 Nm3/min(130 NL/min),流场达到稳定时, 上述双孔底吹VD 精炼炉内的流场及羽流区轮廓, 图中所标出的两个平面分别为两个底吹多孔塞处的中心面。由左图可以看出,羽流区以外区域略靠近自由上界面(熔池表面)处存在一个大环流, 羽流区附近的钢水受黏性力和横向湍流脉动的驱动也做向上运动。当到达溶池表面,由于重力的作用,液相逐渐转做水平流动,当靠近包壁处则转为向下流动。 右图中的羽流区轮廓图是由5%的气体体积分数等值线刻画,可以看出,自下向上,羽流区先向包壁靠近行至熔池高度约一半后开始向包壁相反方向发展,此现象与上述环流相关。
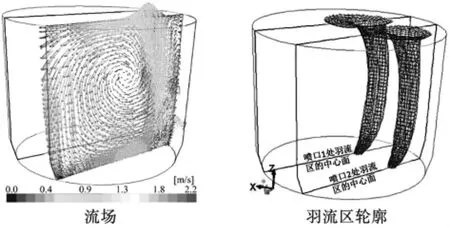
图3 双孔底吹VD 精炼炉内的流场及羽流区轮廓
图4 为总氩气流量130 NL/min,真空处理10 min时,上述双孔钢包内的钢水中[H]和[N]浓度分布。由图可知,[H]与[N]的浓度分布相似,由于羽流区气泡内和钢液面渣眼处产物气体(氮气和氢气)分压相对较低,所以在相应位置会形成低[H]和低[N]区。
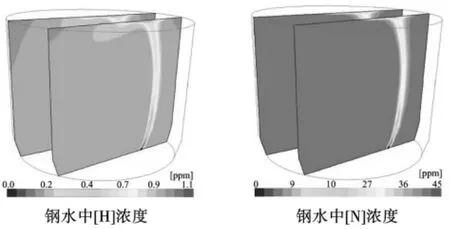
图4 双孔底吹VD 精炼炉内的钢水中[H]和[N]浓度分布
图5 为不同底吹氩气流量条件下钢水中[H]浓度随真空操作时间的变化。 由图可知,吹气初期,钢水中[H]浓度随真空操作时间迅速降低,随后逐渐趋缓。此外,相同真空操作时间下,增大底吹流量,钢水中[H]浓度降低。 由图5 中数据可知,当气体流量从80 NL/min 增大到130 NL/min,同样20 min 的真空操作下,氢的脱除率提高18%。 但是,若进一步增大吹气量至180 NL/min,脱氢率仅提高3%。 相应条件下钢水中[N]浓度随真空操作时间的变化与图5 类似,故不再赘述。 因此,过度增大底吹气体流量对钢水脱气效率无显著提升效果, 反而可能会导致熔渣大量泡沫而威胁生产安全。
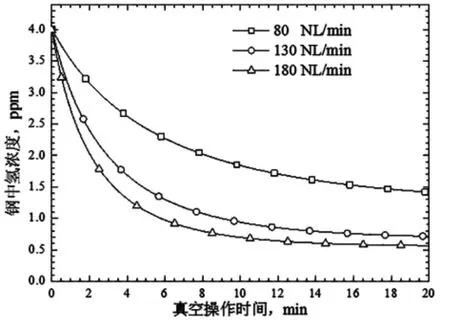
图5 不同底吹氩气流量条件下钢水中[H]浓度随真空操作时间的变化
图6 比较了不同操作条件和钢水条件下上述双孔底吹VD 精炼炉9 炉次钢水中[N]终点浓度的预测值和测量值。 由图可知,钢水中[N]终点浓度的预测值与测量值的最大误差值为3 ppm,吻合度高。因此可以说,本模型具有较高精度,可用于进行VD 精炼过程的相关应用基础研究。
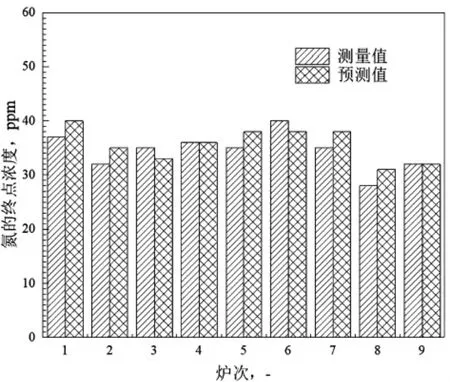
图6 双孔底吹VD 精炼炉9 炉次钢水中氮终点浓度的预测值和测量值
4 结论
(1)基于Euler-Euler 方法,建立了可用于描述真空条件下反应器内气液流动和传质行为的通用计算流体力学(CFD)模型。 将所建立的CFD 模型用于某钢厂在产VD 精炼炉, 具体研究了不同底吹氩气流量条件下熔池中的流场分布和羽流区形貌, 以及钢水中[H]和[N]浓度随真空操作时间的变化规律。
(2)吹气初期,钢水中[H]浓度随真空操作时间迅速降低, 随后逐渐趋缓。 相同真空操作时间下,增大底吹流量,钢水中[H]([N])浓度降低,但过度增大底吹气体流量对钢水脱气效率无显著提升效果。
(3)比较总计9 炉次钢水中[N]终点浓度的预测值和测量值, 发现本模型的最大误差为3 ppm。 因此,本模型具有较高精度,可用于进行VD 精炼过程的相关应用基础研究。
