变截面消声管道耦合Helmholtz腔结构的声学性能

吴卫国, 毕佳楠, 魏 崴

(江苏大学 土木工程与力学学院, 江苏 镇江 212013)

低频声波由于波长较长,难衰减,对其进行有效控制是噪声控制领域中的难点和热点之一.近年来,声学超材料的发展为解决低频噪声问题提供了新的思路.通过对几何结构和形状尺寸的独特设计,具有亚波长特性的声学超材料可以实现负等效质量密度和负等效弹性模量[1-4],从而实现了“小尺寸控制大波长”.

为了增加声学超材料结构的声学控制带宽,文献[5]提出了一种在Helmholtz谐振器上增加小质量和小尺寸的可调节谐振板技术.文献[6]设计了一种基于Helmholtz谐振腔的嵌入式低频宽带隔声装置.文献[7]设计了一种薄膜与Helmholtz谐振腔相结合的声学超材料模型,扩大了其控制带宽,且隔声效果良好.文献[8]设计了一种引入非均匀射孔和多腔深度的微穿孔板吸收器,通过调节各个子腔的深度来控制吸收带宽.文献[9]提出了一种由对称双Helmholtz谐振腔和具有主动控制作用器件组成的新型弹性声学超材料,通过改变电压来实现对噪声的半主动控制.文献[10]设计了一种包含气动驱动系统的Helmholtz腔声学超材料,通过控制气动驱动系统来改变每个单元的空腔深度,从而调整吸声系数峰值对应频率的范围.文献[11]提出电磁调控的铁粉薄膜耦合模型,实现非接触主动调控隔声带隙的操作模式.综上,基于声学超材料的噪声主动控制的研究已取得了众多成果[12-14],目前,现有的声学超材料结构尺寸复杂,制备要求高,因此有必要对具有良好控制效果的、结构简单的非接触式声学超材料进行研究.

为此,本课题组拟设计一种变截面消声管道耦合Helmholtz腔的声学超材料,通过改变消声管道小孔截面形状,对该材料在低频范围内的声学性能进行数值模拟和试验研究,探讨在不改变结构整体几何尺寸的前提下,对声学超材料结构固有频率的可控调谐和低频噪声实现有效控制.

1 声学超材料结构模型设计

1.1 声学超材料结构模型

本课题组设计的变截面声学超材料模型是以Helmholtz谐振腔为基础,由圆柱形的空腔结构和变截面管道消声穿孔板组成.变截面声学超材料结构模型示意图如图1所示,其中二、三、四阶变截面指的是小孔分别由2、3、4个不同内径的小孔截面组成.将变截面Helmholtz谐振腔与普通Helmholtz谐振腔进行对比,研究小孔变截面与非变截面对吸声系数的影响.

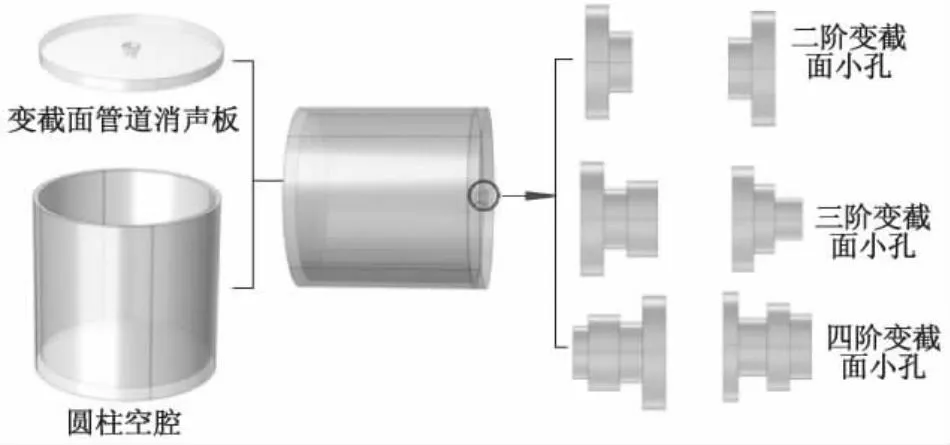
图1 变截面声学超材料结构示意图

1.2 Helmholtz谐振腔吸声理论

结构模型可以简化成Helmholtz谐振腔.由局域共振理论可知,Helmholtz谐振腔的声强透射系数τ计算式[1]为

(1)

式中：ρ0为空气密度;c0为声波在空气中的传播速度;S为空腔截面积;Ra为声阻,声阻很小,计算时可以忽略不计,即Ra=0;Xa为声抗,声抗计算式如下所示：

Xa=ωMa-1/(ωCa),

(2)

式中：Ma为声质量,Ma=dρ0/Sa,其中Sa为小孔截面积,d为小孔深度;ω为角频率,ω=2πf,其中f为频率;Ca为声顺,Ca=Va/(ρ0c02),其中Va为Helmholtz腔的体积.

联合式(1)和(2),得到简化计算式为

(3)

由式(3)可以看出,共振频率与小孔半径、深度以及圆柱空腔的体积有关.

1.3 管道消声理论

文中研究的变截面小孔可简化为小型的扩张式消声管道,示意图如图2所示,S1和S2分别为消声管道中小孔和大管道的横截面积,D为消声管道的长度.

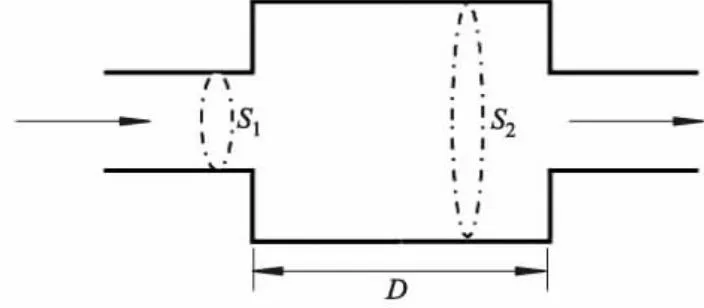
图2 扩张式消声管道示意图

根据管道消声理论,声波通过扩张式管道时,二阶扩张式消声器的声强透射系数为

(4)

从Helmholtz局域共振理论和管道消声理论可以看出,将Helmholtz腔中的小孔设计成多阶变截面小孔管道,既满足了Helmholtz腔局域共振理论的优势,即对中低频声波选择性强,又通过扩张式管道消声理论解决了其吸声系数峰值对应频率范围较为狭小的缺陷,从而实现了声学超材料结构在低频范围内声学性能的可控调谐功能.

2 数值分析

2.1 声学超材料结构的吸声性能

根据所建立的声学超材料结构模型,运用COMSOL软件对设计的变截面声学超材料单元模型的声学特性进行数值分析.图3为变截面Helmholtz谐振腔声学超材料结构的剖面图,其中外部声波从结构左侧进入内部,依次经过内径为r1、r2和r3等多阶变截面小孔.文中的变截面小孔是由多个不同半径的小孔叠加组成,每一个小孔的半径根据实际需求进行改变.

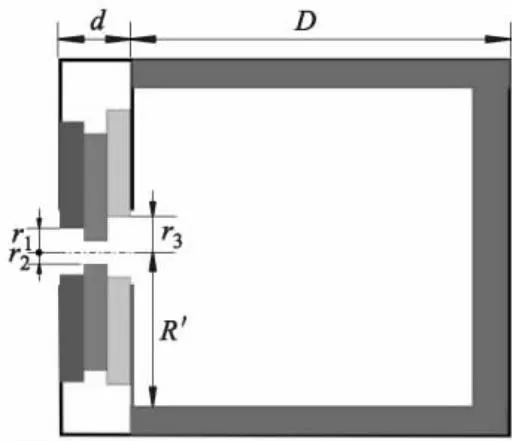
图3 变截面声学超材料结构的剖面图

设计的变截面声学超材料结构单元尺寸如下：小孔深度d=3.0 mm;小孔半径以二阶变截面为例进行数值分析,r1=1.5 mm,r2=1.5 mm,r3=1.1,1.3,1.5 mm;腔体深度D=40.0 mm;腔体半径R′=15.0 mm.整个结构单元由金属铝制成,其密度为2 700 kg/m3,泊松比为0.33,杨氏模量为71.0 GPa.图4为二阶变截面小孔r3=1.1,1.3,1.5 mm时结构的吸声系数-频率曲线.

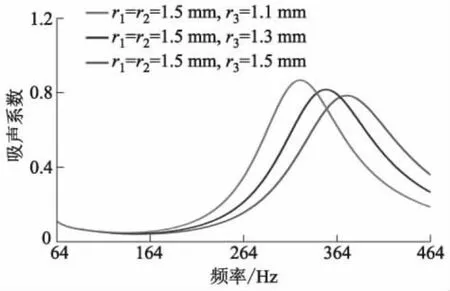
图4 二阶变截面小孔r3=1.1,1.3,1.5 mm时结构的吸声系数-频率曲线

对比具有变截面小孔(r3=1.1,1.3 mm)的Helmholtz腔结构与具有普通小孔(r3=1.5 mm)的Helmholtz腔结构,两者空腔的深度与小孔深度保持一致.由图4可知,随着小孔截面的变化,声学结构的吸声系数峰值也发生变化.具有变截面小孔的Helmholtz腔结构达到吸声系数峰值时的频率低于普通小孔的Helmholtz腔结构,并且吸声系数峰值较高.可见,通过改变截面小孔的结构尺寸,可以在低频范围内调控声学超材料结构的吸声系数峰值.

2.2 二阶变截面小孔

选用的Helmholtz腔二阶变截面小孔深度d=2.0 mm,其中一组二阶变截面小孔r1=r2=1.5 mm,小孔半径r3=1.1,1.3,1.5 mm;另一组小孔r1=r2=1.0 mm,r3=0.6,0.8,1.0 mm.腔体深度D=40.0 mm,腔体半径R′=15.0 mm.

为了计算具有二阶变截面小孔的Helmholtz腔结构在不同变截面小孔半径下的吸声系数,绘制了小孔深度d=2.0 mm时具有二阶变截面小孔的声学结构吸声系数-频率曲线,如图5所示.由图5a可知：通过改变二阶变截面小孔截面半径,可以改变吸声系数峰值所对应的频率;二阶变截面小孔变截面半径r3减小,对应的Helmholtz腔结构的吸声系数峰值对应的频率向低频移动.相较r3=1.0 mm腔结构吸声系数峰值为0.635,r3=0.6,0.8 mm腔结构吸声系数峰值有明显提高,分别为0.997和0.949,3条曲线变化趋势相同.

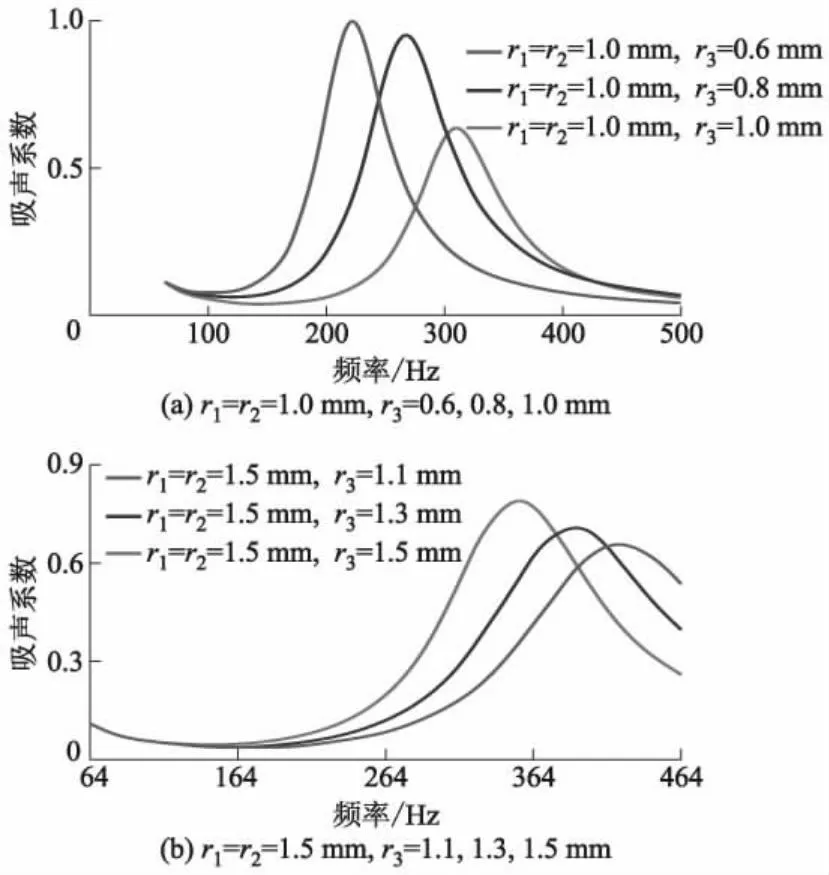
图5 不同小孔变截面半径下二阶变截面Helmholtz腔结构的吸声系数-频率曲线

由图5b可知,二阶变截面小孔半径为r1=r2=1.5 mm,r3=1.1,1.3,1.5 mm时,吸声曲线变化趋势与图5a相同,吸声系数峰值对应的频率随着二阶变截面小孔半径r3的增大向高频移动.

2.3 三阶变截面小孔

保持Helmholtz腔体深度和腔体半径不变,改变变截面小孔深度和小孔半径,由二阶变截面小孔改为三阶变截面小孔,单阶小孔深度为1.0 mm,小孔总深度d=3.0 mm,r1=1.5 mm,r2=1.1,1.3 mm,r3=1.1,1.3,1.5 mm.不同变截面小孔半径下,小孔深度d=3.0 mm时三阶变截面小孔半径(r2和r3)的声学结构吸声系数-频率曲线见图6.

由图6可知：三阶变截面小孔r1=1.5 mm,r2=1.1 mm时,r3=1.1,1.3,1.5 mm的吸声系数峰值分别为0.907、0.887、0.856,对应的频率分别为307、329、348 Hz;r1=1.5 mm,r2=1.3 mm时,r3=1.1,1.3,1.5 mm的吸声系数峰值分别为0.885、0.845、0.825,对应的频率分别为318、340、354 Hz.可见,相较r3=1.5 mm,r3=1.1 mm的三阶变截面小孔吸声系数峰值对应频率较低;相较二阶变截面小孔,三阶变截面小孔的吸声系数峰值有所衰减,吸声系数峰值对应的频率向低频移动.

由图5和图6可知,变截面小孔的深度和小孔变截面半径对吸声系数峰值所对应频率的大小有显著影响,频率随着变截面小孔深度的增加而减小,随着变截面小孔半径的增加而增加,吸声系数峰值与变截面小孔阶数有关,阶数增加,吸声系数峰值减小.

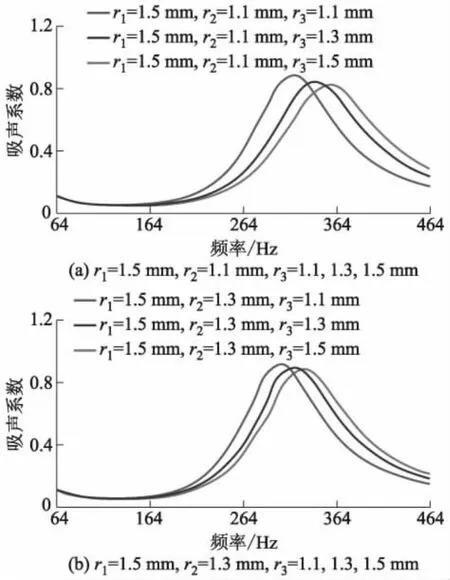
图6 不同小孔变截面半径下三阶变截面Helmholtz腔结构的吸声系数-频率曲线

综上,考虑到声学超材料结构在更低频范围内的吸声效果与结构的轻便性,选择小孔截面阶数较多、变截面小孔半径较小的Helmholtz腔结构.如若考虑声学超材料结构吸声效果的优先性,应选择小孔截面阶数较少的变截面小孔构成的Helmholtz腔结构.

3 声学性能试验

为了验证理论分析与数值模拟结果,文中运用阻抗管声学测量系统,对设计的声学超材料结构的声学特性进行试验,采用的测量方法为传递函数法.声学性能试验选用的阻抗管声学测量系统示意图如图7所示.

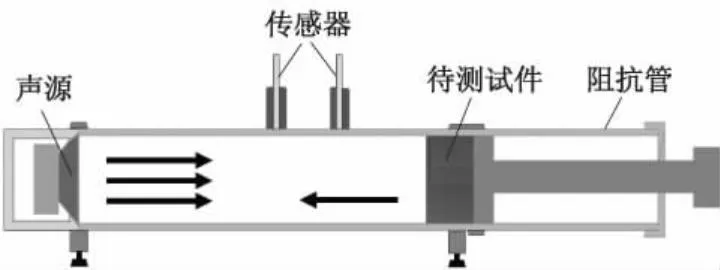
图7 阻抗管声学测量系统示意图

根据阻抗管声学测量系统的阻抗管尺寸,分别制备了五元胞二阶和三阶变截面消声管道耦合Helmholtz腔声学超材料结构,并选用轻质的金属铝材.每个元胞的腔深度为40.0 mm,腔内半径为15.0 mm,选取的多阶变截面小孔总深度为3.0 mm,单阶小孔深度为1.0 mm.各阶小孔分尺寸如下：三阶变截面小孔r1=1.5 mm,r2=1.3 mm,r3=1.1,1.3,1.5 mm;二阶变截面小孔r1=1.5 mm,r2=1.5 mm,r3=1.1,1.3,1.5 mm.五元胞二阶声学超材料结构实物模型的照片如图8所示.

图8 五元胞二阶声学超材料结构实物模型照片

为了保证试验精度,将制备好的试件用声学胶带缠绕后涂抹凡士林,不仅防止漏声,同时还可增加试件的润滑度,便于放置于阻抗管中.多次试验得到二、三阶变截面消声管道耦合Helmholtz腔结构的吸声系数-频率试验曲线分别如图9和图10所示.

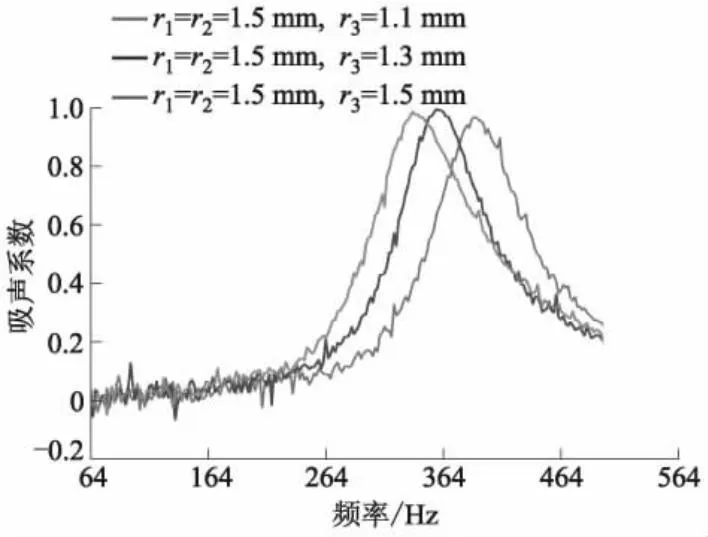
图9 二阶变截面小孔r1=r2=1.5 mm,r3=1.1,1.3,1.5 mm时吸声系数-频率试验曲线

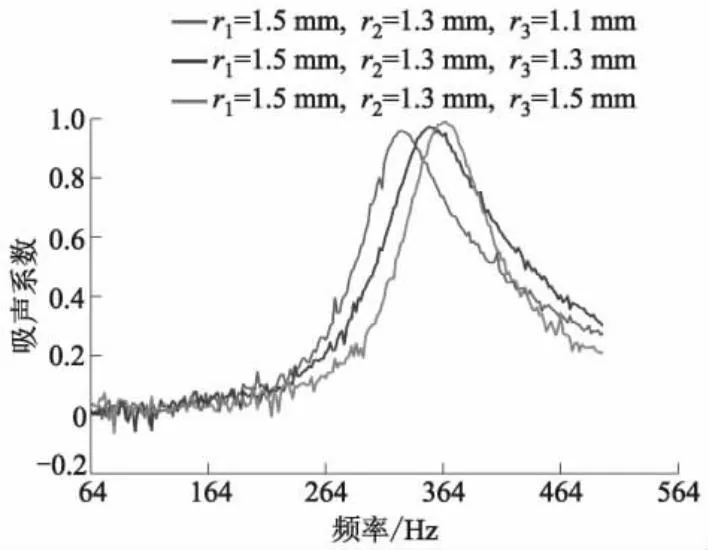
图10 三阶变截面小孔r1=1.5 mm,r2=1.3 mm,r3=1.1,1.3,1.5 mm时吸声系数-频率试验曲线

图9中,r3=1.1,1.3,1.5 mm时吸声系数峰值分别为0.988、0.996、0.967,对应频率分别为338、358、390 Hz.由图10可知,r3=1.1,1.3,1.5 mm时吸声系数峰值分别为0.961、0.944、0.989,所对应频率分别为328、352、366 Hz.可见,随着r3减小,吸声系数峰值变化并不大,所对应的频率向低频移动.因此,由图9、10可知,r3由1.1 mm增加到1.5 mm,其吸声系数峰值所对应频率分别增加了52 Hz和38 Hz,截面半径大小变化相同时,二阶变截面小孔的结构吸声系数峰值所对应频率改变优于三阶变截面小孔的结构,但是三阶变截面小孔在更低频范围内可以展现良好的吸声性能.试验结果证明：在声激励作用下,声波经过类似于消声管道的变截面小孔,由于声阻作用,在传播过程中声能量被消耗,声波衰减,因而该多阶变截面小孔耦合Helmholtz腔结构的吸声效果优于普通Helmholtz腔.而且该声学超材料结构吸声系数峰向更低频区域移动,低频范围为200～600 Hz,拓宽了吸声系数峰值对应的低频范围,获得了良好的试验效果.

4 结 论

1) 设计制备了一种变截面声学超材料结构,通过理论计算以及运用COMSOL有限元软件,对结构的声学性能进行了系统分析.该变截面声学超材料在低频范围(200～600 Hz)内具有良好的吸声效果,且通过改变变截面小孔尺寸,可实现对吸声系数峰值对应频率的可控调谐.

2) 试验验证了变截面声学超材料结构的吸声性能,其吸声系数峰值所对应频率的最大调谐量为52 Hz,有效拓宽了声学超材料吸声系数峰对应的低频范围.

3) 在该变截面声学超材料结构厚度不变的情况下,吸声系数峰可在一定低频范围内移动,实现了吸声系数峰对应频率范围的非接触式可控调谐,拓宽了结构的吸声系数峰对应的频率范围,对低频噪声的宽带控制研究提供了新的思路.