基于遗传算法的汽车主动悬架变论域模糊PID控制

薛文平, 张春玲

(江苏大学 电气信息工程学院, 江苏 镇江 212013)

汽车悬架是车轮与车身之间的连接装置,对汽车的行驶安全性和舒适性至关重要.根据控制形式不同,悬架通常分为被动悬架、半主动悬架和主动悬架3类[1].相比于被动悬架和半主动悬架,主动悬架能够适应不同车辆运行状况,兼顾汽车的操纵稳定性与乘坐舒适性[2],是悬架产业发展的重要趋势.

作为主动悬架的重要组成部分,控制器的设计问题一直是悬架研究的重点.目前已有多种先进控制方法被应用于主动悬架领域,如：自适应控制[3-4]、H∞控制[5-6]、滑模控制[7]、模糊控制[8]、有限时间控制[2]等.其中模糊控制具有不依赖于系统模型、建构设计较为简单和鲁棒性强等特点,在主动悬架控制领域得到了广泛应用.文献[9]研究了悬架系统自适应模糊最优反馈控制问题,设计了模糊观测器来估计不可测状态.文献[10]同时考虑主动悬架系统的参数变化、外部扰动和摩擦力效应等非线性因素,提出了一种基于粒子群优化的无模型模糊控制控制器.文献[11]将传统比例-积分-微分(proportional-integral-differential,PID)控制、模糊逻辑以及智能优化技术相结合,设计了主动悬架系统最优模糊PID控制器.

上述基于模糊逻辑的主动悬架控制方法在改善车辆乘坐舒适性和行驶安全性方面取得了不错的效果.但是,模糊变量的论域固定,且论域的确定大都依赖于专家经验,这在一定程度上影响了悬架系统的控制性能.针对传统模糊控制中变量论域固定不变这一缺点,文献[12]提出了变论域的思想,在模糊规则不变的前提下,通过调节伸缩因子来实现论域变化.当误差较大时,膨胀论域,加快控制系统响应速度;当误差较小时,收缩论域,其效果等同于增加模糊规则,使模糊控制器在结构复杂度不变的前提下,提高灵敏度.文献[13]利用模糊神经网络结构来调整伸缩因子的变化,实现了半主动汽车悬架系统的变论域模糊控制.目前,关于伸缩因子并没有统一的表达形式,而描述函数以其简单、直观、易于实现的特点,成功应用于变论域模糊控制的论域调节中[14-15].值得注意的是,伸缩因子描述函数中所涉及的参数通常使用试凑法得到.然而,这些参数的选择会影响变论域模糊控制的效果.

基于上述分析,同时考虑模糊PID控制兼备PID与模糊控制的各自优点[11],笔者提出一种基于遗传算法(genetic algorithm, GA)的汽车主动悬架系统变论域模糊PID控制方法.该方法中的伸缩因子采用描述函数表达形式.在此基础上,采用GA来优化描述函数中的参数以改善控制效果.最后,通过仿真与比较验证所提控制方法的有效性和鲁棒性.

1 1/4车主动悬架系统模型

采用的1/4车主动悬架系统结构如图1所示,其中：ms为簧载质量;mu为非簧载质量;cs为悬架阻尼系数;ks为悬架的弹性系数;kt为轮胎弹性系数;zs(t)为簧载质量垂向位移;zu(t)为非簧载质量垂向位移;zr(t)为路面垂向位移;f(t)为悬架的主动控制力.

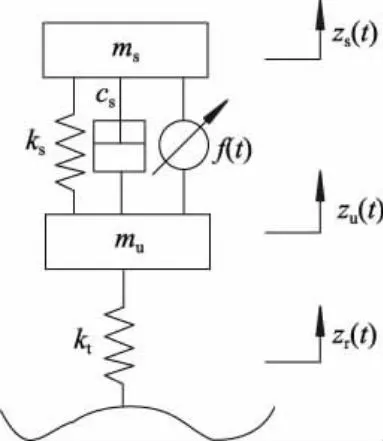
图1 1/4车主动悬架模型

根据牛顿第二定律,1/4车主动悬架系统的动力学模型可表示为

(1)

为得到系统的状态空间模型,状态向量定义为

x(t)=[x1(t)x2(t)x3(t)x4(t)]T,

(2)

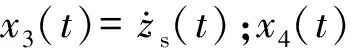
输出向量为

(3)

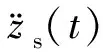
通过推导,可将式(1)表示为如下状态空间模型：

(4)

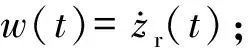
2 变论域模糊PID控制原理

变论域模糊PID控制系统结构如图2所示,其中：α、β分别为调节输入、输出论域的伸缩因子.

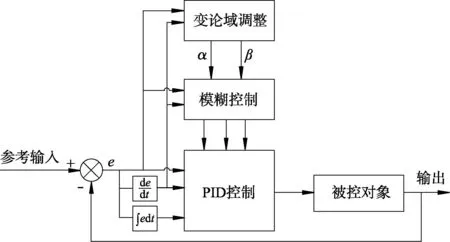
图2 变论域模糊PID控制结构

设模糊控制输入e及其导数ec对应的论域分别为[-E,E]、[-Ec,Ec],输出y对应的论域为[-Y,Y].以论域[-E,E]为例,其伸缩变化情况如图3所示,其中：NB、NM、NS、Z、PS、PM、PB分别表示模糊语言值的负大、负中、负小、0、正小、正中和正大.对于论域的伸缩因子,按照文献[14-15]采用描述函数的方式确定其具体形式.输入论域[-E,E]、[-Ec,Ec]及输出论域[-Y,Y]对应的伸缩因子α1、α2、β分别采用如下描述函数：

(5)

(6)

(7)

式中：τ为大于0的指数项系数;ε是无限接近于0的正数;E为输入e的范围边界值;Ec为输入ec的范围边界值;K为常数;n为输入个数;Qi为模糊控制输入的权重系数;θ为积分变量;β0为输出论域伸缩因子初值,一般取值为1.

图3 论域变化示意图

在伸缩因子的作用下,模糊控制输入输出的论域变为[-α1E,α1E]、[-α2Ec,α2Ec]和[-βY,βY].

3 基于GA的变论域模糊PID控制

通过仿真发现：式(5)-(7)中参数τ和Qi的取值会影响变论域模糊控制的效果.目前,这些参数取值通常采用试凑法获得.为进一步改善主动悬架系统的控制性能,利用高效、全局的GA来寻找变论域模糊PID控制器中最佳的描述函数参数.

3.1 优化向量及优化目标

对于给出的1/4车主动悬架系统,变论域模糊PID控制器中(图2),模糊控制的2个输入分别选为车身垂向速度期望值和实际值之间的误差ev以及车身垂向加速度期望值与实际值之间的误差ecv;模糊控制的输出为PID控制中3个参数的增量.选取描述函数中参数τ和Qi组成的向量h=[τQi]为GA优化的优化向量.

车身垂向加速度是评价车辆在运行过程中是否平稳的关键指标.因此,选取车身垂向加速度均方根aRMS作为GA优化的目标函数.此外,考虑时域硬约束[5],即满足轮胎接地性与悬架行程限制,可将基于GA的论域模糊PID控制转化为如下优化问题：

(8)

式中：zmax为悬架行程的上限值;kt(zu(t)-zr(t))<(ms+mu)g为轮胎动载荷不超过静载荷,即轮胎相对动载荷不超过1(保证轮胎不间断接触地面).

3.2 控制器设计

基于GA的变论域模糊PID(简称GA-变论域模糊PID)控制器设计流程如图4所示.对于优化问题式(8)中的约束条件,采用罚函数方法将其转化成无约束优化问题.图4中的停止条件设置为达到最大迭代次数或给定相对误差,带变论域模糊PID控制的主动悬架系统仿真框图如图5所示,其中F为轮胎动载荷.

图4 GA-变论域模糊PID控制器设计流程

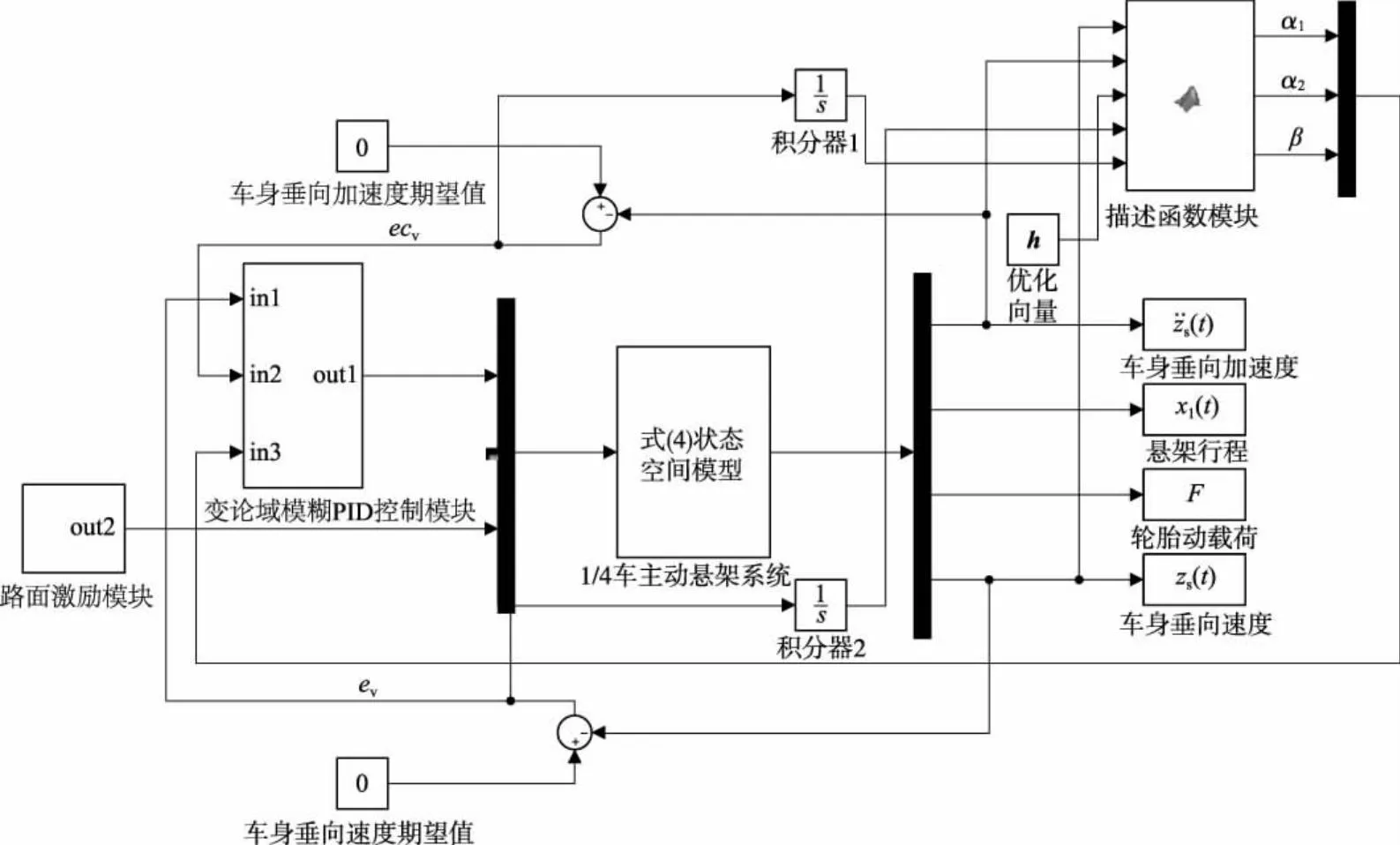
图5 带变论域模糊PID控制的主动悬架系统仿真框图

图5中的1/4车主动悬架系统采用式(4)给出的状态空间模型;路面激励模块采用C级随机路面激励;描述函数模块为根据式(5)-(7)编写的MATLAB函数模块,模块的输入h为GA的优化向量,模块的输出为变论域模糊PID控制所需的伸缩因子α1、α2和β,ev和ecv的伸缩因子分别为α1、α2,PID控制中3个参数增量对应的伸缩因子均为β;变论域模糊PID控制模块内嵌一个实现变论域模糊控制的MATLAB函数模块.

4 仿真与结果分析

4.1 仿真设置

仿真过程中,GA的主要参数如下：种群数为20 个,最大迭代次数为20 次,交叉概率为0.8,变异概率为0.2.模糊隶属度函数选取如图3所示的三角形隶属度函数.随机路面模型主要参数如下：参考空间频率n0=0.1 m-1;路面不平度系数Gq(n0)=0.000 256 m3;车辆行驶的速度v=12.5 m/s.1/4车主动悬架模型涉及的主要参数如下：ms=320 kg,mu=40 kg,ks=18 kN/m,cs=1 kN·s/m,kt=200 kN/m,zmax=0.08 m.模糊控制输出ΔKP、ΔKI和ΔKD所对应的模糊分割数均为7个,相应的模糊规则如表1-3所示.

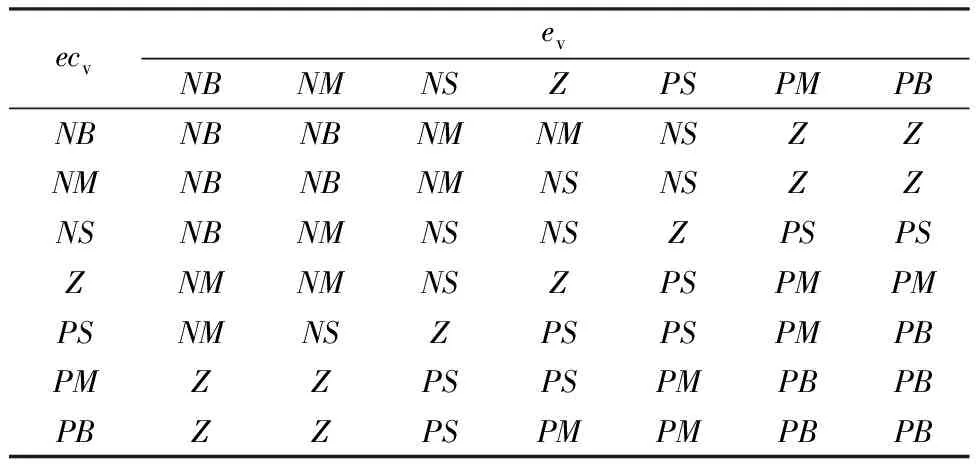
表1 ΔKP的模糊规则

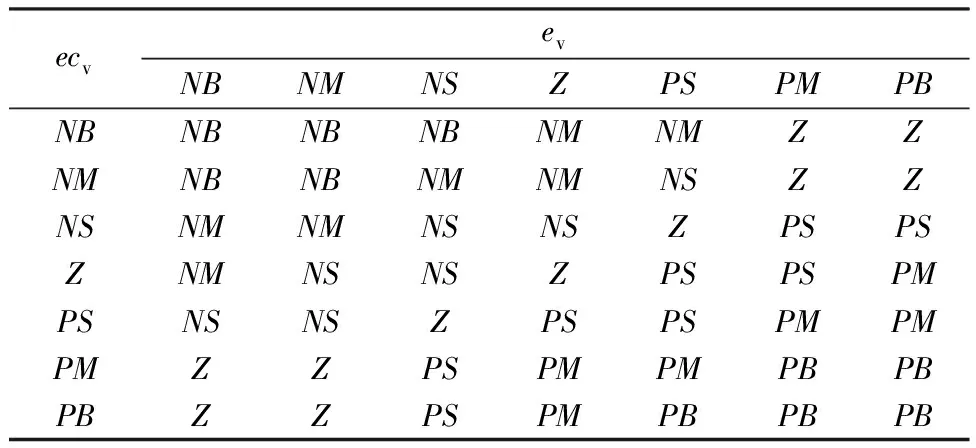
表2 ΔKI的模糊规则

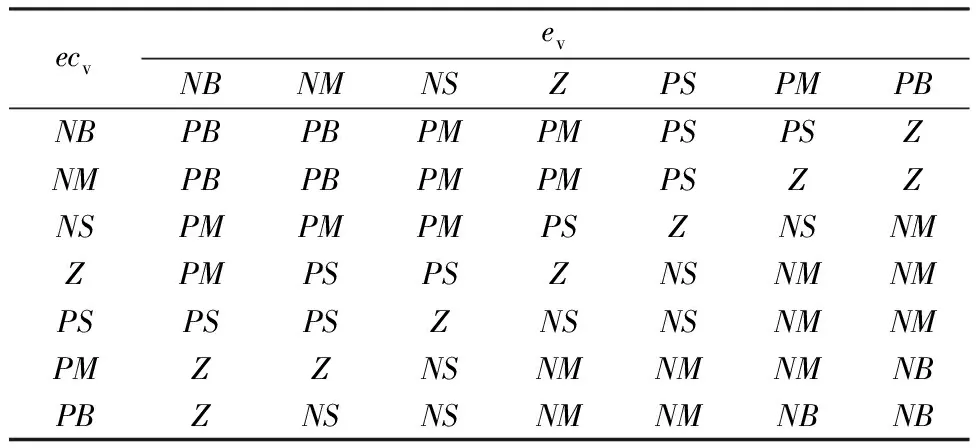
表3 ΔKD的模糊规则

4.2 不同控制方法比较

多次运行GA,优化变论域描述函数参数τ、Q1和Q2.选取5次优化运行对应的变论域模糊PID控制结果如表4所示,其中amax为车身垂向加速度峰值.

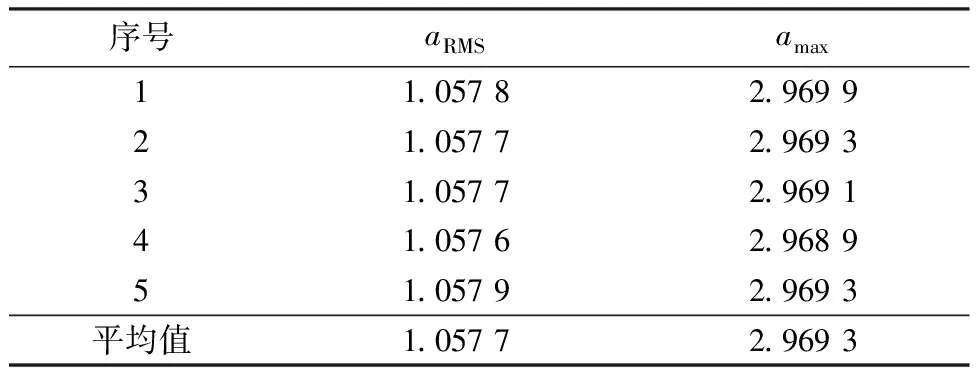
表4 基于GA优化的变论域模糊PID控制结果 m/s2

为了验证所提出GA-变论域模糊PID控制方法的优越性,将其与未进行优化的变论域模糊PID控制、模糊PID控制、PID控制以及被动控制的振动控制效果进行对比.对于PID控制,为了对比的一致性,选择车身垂向速度期望值和实际值之间误差的比例、积分与微分项作为控制器输入.KP、KI、KD参数根据试凑法选择如下：KP=250,KI=1,KD=50.对于模糊PID控制,其模糊控制的输出为PID控制中3个参数的增量,3个参数的初始值和上述PID控制保持一致.对于GA-变论域模糊PID控制,式(5)-(7)中的参数选择如下：ε=0,K=10,β0=1,变量τ、Q1、Q2的优化区间均设为[0, 1].对于未优化的变论域模糊PID控制,τ、Q1、Q2选为优化区间的中间值：τ=0.5,Q1=0.5,Q2=0.5.

当ms=320 kg,v=12.5 m/s时,不同控制方法下,aRMS、amax如表5所示,其中：η1、η2分别为相比于被动控制aRMS、amax的降幅;GA-变论域模糊PID控制对应表4中第1组优化结果,优化后,τ=0.003 4,Q1=0.033 6,Q2=0.926 4.

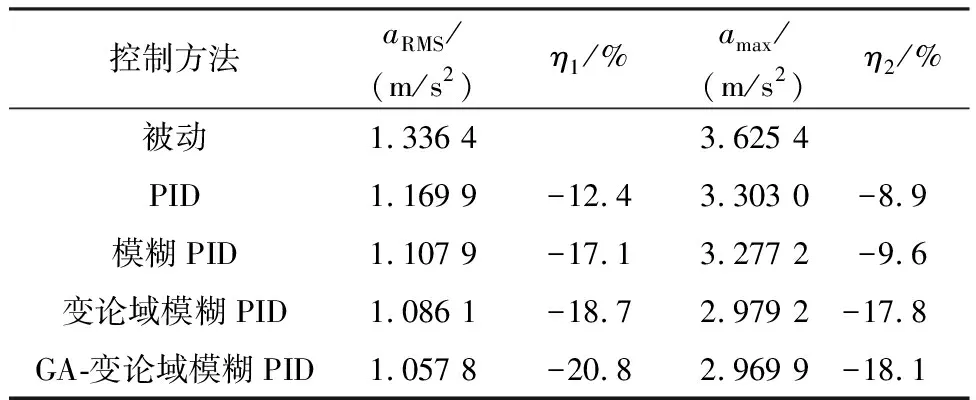
表5 不同控制方法结果对比

从表5可以看出：GA-变论域模糊PID控制对应的aRMS和amax比其他几种控制器都要小.

不同控制对应的车身垂向加速度响应对比曲线如图6-9所示.不同控制器对应的悬架系统车身垂向加速度功率谱密度(power spectral density, PSD)响应对比曲线如图10所示.GA-变论域模糊PID控制器所对应的悬架行程响应曲线和轮胎相对动载荷响应曲线分别如图11、12所示.

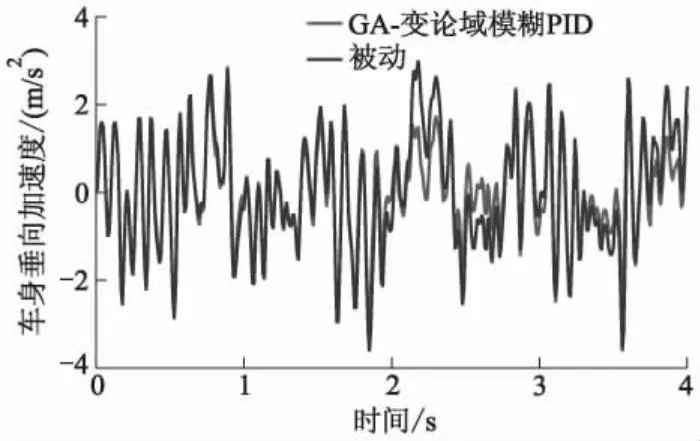
图6 GA-变论域模糊PID控制与被动控制的车身垂向加速度响应对比曲线

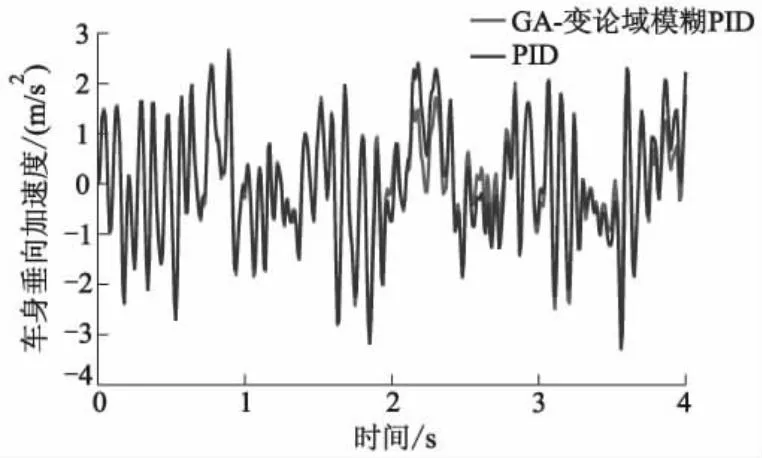
图7 GA-变论域模糊PID控制与PID控制的车身垂向加速度响应对比曲线

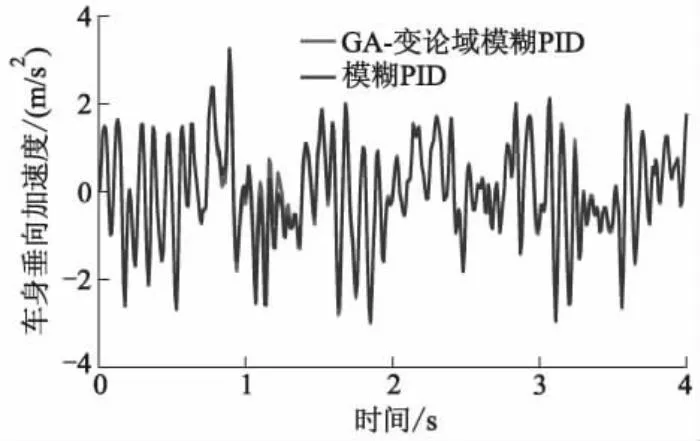
图8 GA-变论域模糊PID控制与模糊PID控制的车身垂向加速度响应对比曲线

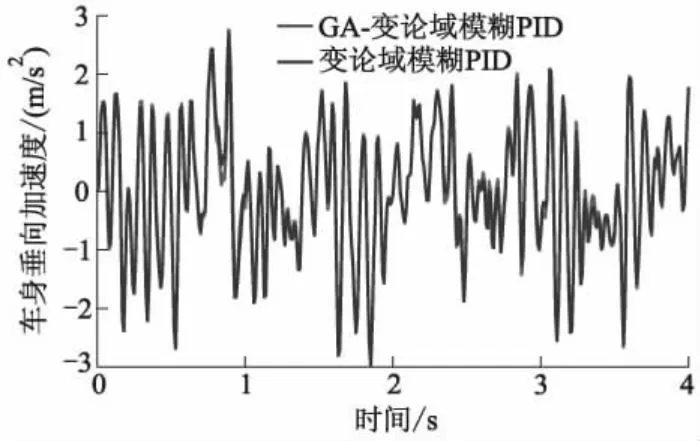
图9 GA-变论域模糊PID控制与变论域模糊PID控制的车身垂向加速度响应对比曲线

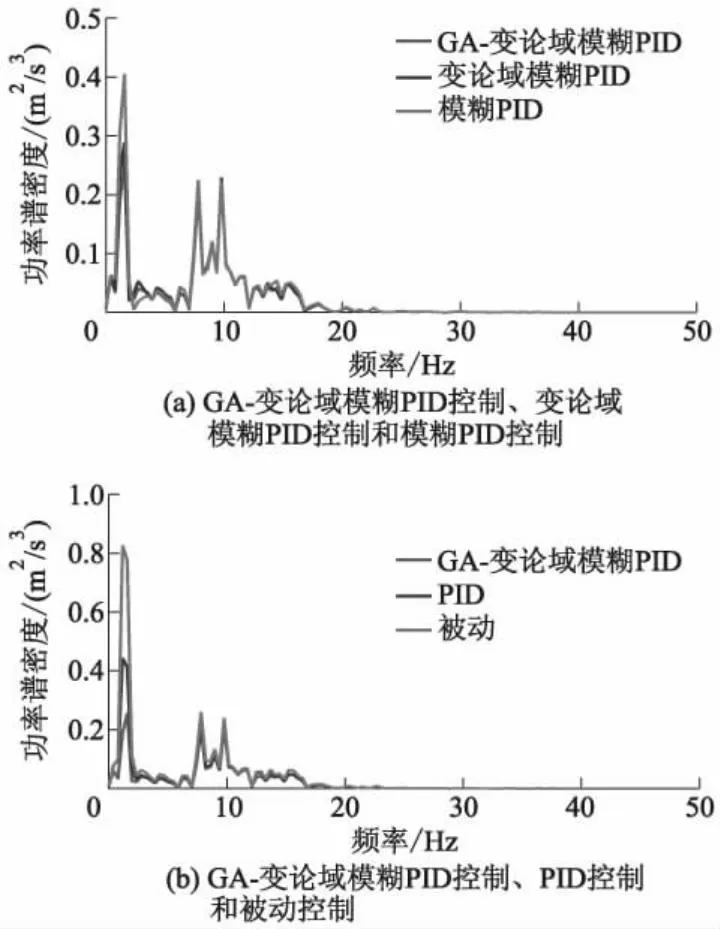
图10 车身垂向加速度功率谱密度响应对比曲线

图11 悬架行程响应曲线

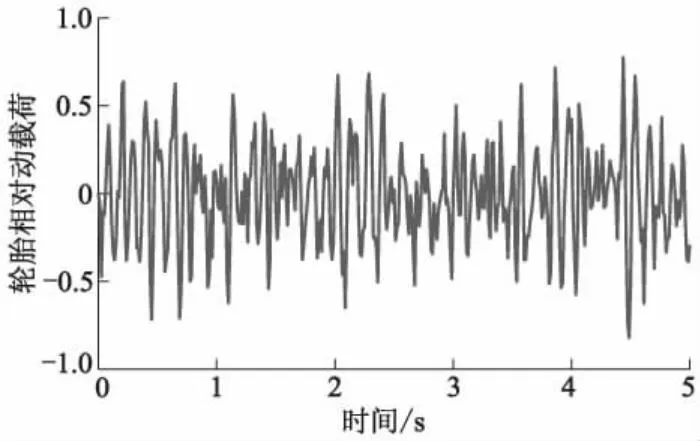
图12 轮胎相对动载荷响应曲线

从图6-10可以看出：相较于其他控制方法,GA-变论域模糊PID控制可以明显降低车身垂向加速度,改善乘坐舒适性.从图11、12可以看出：GA-变论域模糊PID控制在降低车身垂向加速度的同时,还能保证闭环悬架系统满足悬架行程和轮胎相对动载荷2个时域硬约束.

4.3 鲁棒性分析

车辆在行驶过程中,经常会遇到装载货物、上下乘客等情况.这些情况会导致悬架系统簧载质量发生变化.此外,为了适应不同路况,车辆行驶速度也会发生变化.为了验证所提控制方法在簧载质量和车辆行驶速度不确定情形下的鲁棒性,分别对簧载质量ms变化±10%、车速v变化±20%这4种情况进行仿真试验,4种情况如下：①ms=352 kg,v=12.5 m/s;②ms=288 kg,v=12.5 m/s;③ms=320 kg,v=15.0 m/s;④ms=320 kg,v=10.0 m/s.这4种情况下,不同控制方法的aRMS和amax对比如表6-9所示.

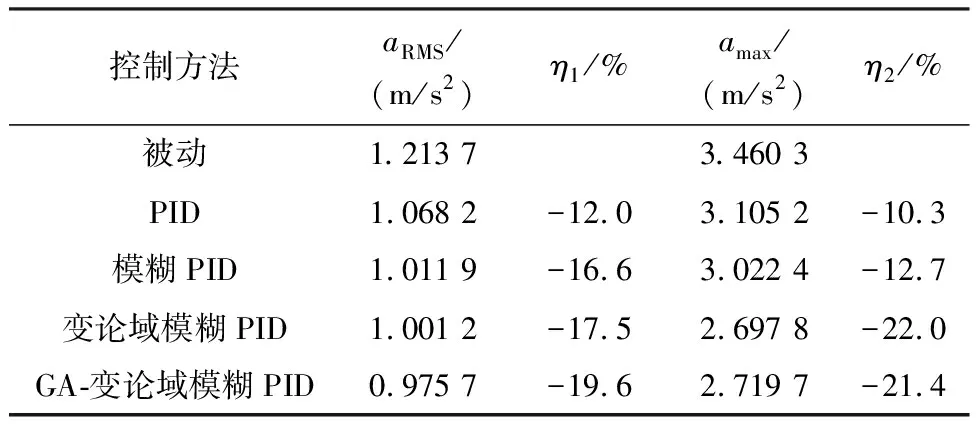
表6 ms=352 kg,v=12.5 m/s时不同控制的aRMS和amax对比

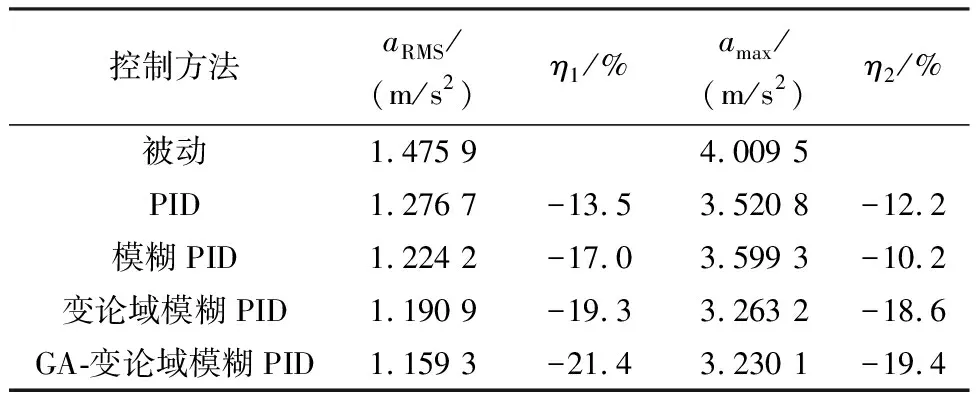
表7 ms=288 kg,v=12.5 m/s时不同控制的aRMS和amax对比

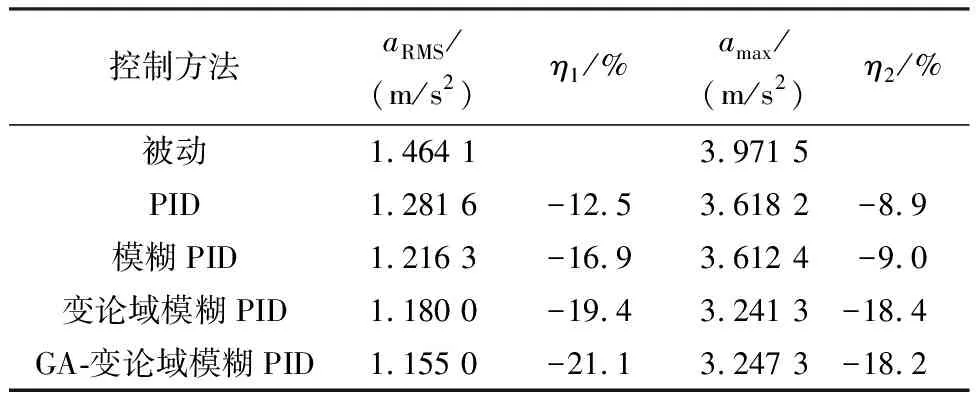
表8 ms=320 kg,v=15.0 m/s时不同控制的aRMS和amax对比

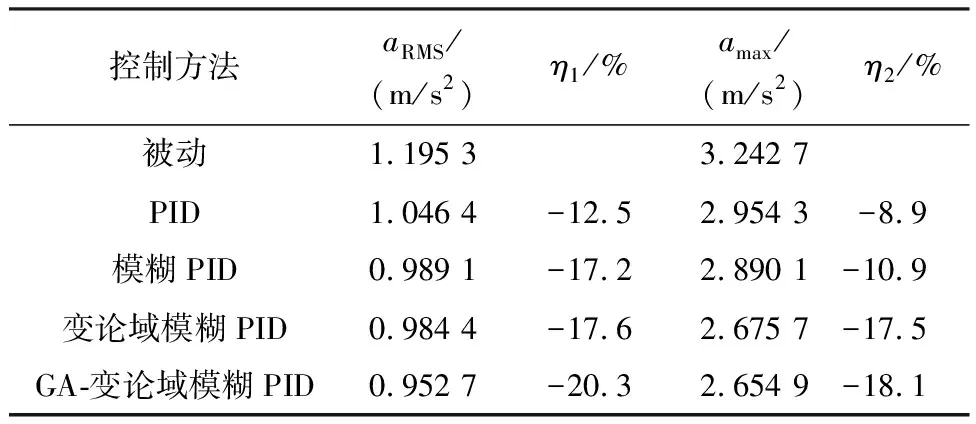
表9 ms=320 kg,v=10.0 m/s时不同控制的aRMS和amax对比

簧载质量、车辆行驶速度变化的情况下,不同控制方式下aRMS的对比如图13所示.从表6-9、图13可以看出：在簧载质量和车辆行驶速度改变的情况下,对比其他几种控制方法,GA-变论域模糊PID控制依然可以有效降低车身垂向加速度,提高乘坐舒适性,保证行驶安全性.仿真结果表明所提控制方法对簧载质量和车辆行驶速度不确定性具有较强的鲁棒性.

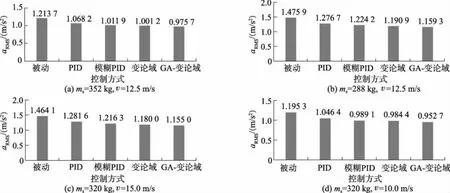
图13 不同控制方式下aRMS的对比

5 结 论

将变论域思想与模糊PID控制结合,提出一种基于GA的主动悬架系统变论域模糊PID控制方法.为了改善控制器减振效果,采用GA来优化伸缩因子描述函数中的参数.仿真结果表明：所提控制方法能有效提高车辆乘坐舒适性,并保证闭环系统满足悬架行程和轮胎相对动载荷硬约束.此外,该方法对簧载质量和车辆行驶速度不确定性具备较强的鲁棒性.在未来的研究中,将会把该控制方法推广至1/2车和整车主动悬架系统.