回收模式相异下消费者偏好对制造商合作策略的影响
2024-01-13刘名武
蒋 琼,王 勇,刘名武
(重庆交通大学 经济与管理学院 重庆 400074)
0 引言
如何合理化和规范化处理废旧回收产品,提高产品的回收利用率是当前社会普遍关注的焦点问题。近年来国家也出台了相关政策意见以鼓励实施规范化和智能化回收,如2021年12月21日,生态环境部等部门印发《“十四五”时期“无废城市”建设工作方案》,提出加快构建废旧物质循环利用体系,推进垃圾分类收运与再生资源回收“两网融合”[1]。随着互联网技术的不断成熟,在不同层面上为环保设备进行智能化和信息化管理提供了更多便利,部分城市(区域)的回收工作开启了“互联网+智能”垃圾回收分类的新模式[2]。在理论分析中,也有部分国内外学者对智能回收新模式展开了相关研究,如WANG等[3]、ZHOU等[4]、蒋琼等[5]。本文涉及的智能回收主要指从事回收业务的经营者通过在社区、街道、住宅楼下等位置布局智能回收设施以实现消费者废旧物品的自主回收,从而达到废旧物品的循环再利用,因此将从事此类回收方式的经营者统称为智能回收商。在智能回收的日常运营中,需要消费者根据个人的回收模式选择偏好,将部分废旧物品(如饮料瓶、废纸、金属等)自主投递到智能回收箱以获得一定的产品回收报酬,然后智能回收商再将回收箱收置的废旧产品进行打包运输至回收中心进行分拣、转运、转售处理,以实现回收产品的循环再生利用。制造商作为回收再制造的主体,面对传统的回收模式与新兴的智能回收模式,该如何进行回收模式合作以及合作后对供应链成员的绩效会产生怎样的影响都需要进一步的探讨和分析。基于此,本文在传统回收与智能回收背景下,考虑两种回收方式的差异以及消费者对智能回收的偏好,分析制造商不同合作策略下供应链各成员的最优决策,并进一步探讨消费者的回收偏好对最优决策的影响,这对研究竞争回收下制造商的合作问题具有一定的理论价值和现实意义。
关于竞争回收渠道的研究,学者主要集中讨论了由制造商、零售商、第三方或再制造商两两组合的竞争回收渠道。GIRI等[6]分析了制造商通过网络渠道与第三方同时参与产品回收时的回收定价决策和制造商最优联盟策略选择;WANG等[7]探讨了再制造商分别与制造商和零售商同时回收下制造商的定价策略和回收渠道配置问题;GIRI等[8]讨论了制造商自建网络回收渠道和传统回收者共同回收下的回收决策问题;MATSUI[9]考虑回收经销商通过自建网络回收渠道和第三方回收商组成的双回收渠道逆向供应链,分析了何时决策旧产品回收价格对回收经销商、第三方回收商和消费者的影响;WEI等[10]探究了由零售商、第三方和再制造商两两组合竞争回收情形下再制造商最优定价和最大化利润决策的影响;HE等[11]提出了由制造商和第三方回收商组成的闭环供应链模型,分析竞争与垄断回收情形下渠道的便捷性对消费者回收的影响;路应金等[12]构建了由零售商和第三方组成的双回收渠道决策模型,以分析第三方规模经济效应强弱对供应链渠道结构决策的影响;陈建华等[13]分析了由零售商、第三方和再制造商不同回收组合下供应链各成员的最优价格、回收率和最优利润决策问题。同时,也有部分学者对其他回收形式进行分析,如刘慧慧等[14]考虑正规回收渠道与非正规回收渠道的市场竞争,分析政府补贴和市场合作对正规回收渠道扶持作用的影响;刘珊等[15]构建了两个第三方回收者共同竞争情形下的博弈决策模型以分析企业社会责任对供应链成员的定价策略和利润决策的影响。
关于闭环供应链中合作策略的研究,TIAN等[16]分析了不同竞争环境下制造商的单独或联合回收合作策略对社会福利的影响;WEI等[17]分析了在两个竞争回收者共同回收下制造商的整合策略对供应链成员利润的影响;WU等[18]考虑回收中心通过自建网络回收渠道和第三方回收商进行回收合作,并采取收益分享契约以分配合作后的利润;FENG等[19]考虑由两个制造商和多个回收商组成的多层次竞争回收再制造供应链博弈模型,探讨了制造商和回收商的最优定价决策与供应链成员绩效水平之间的关系;WANG等[20]考虑制造商的企业社会责任和公平关切下构建了以零售商作为渠道领导者的两级闭环供应链博弈模型,以探讨信息不对称和公平问题对闭环供应链绩效的影响;聂佳佳等[21]考虑在零售商回收模式下制造商参照其回收投入和回收努力程度设计了相关的回收激励合同;郑本荣等[22]研究了由制造商与第三方同时参与回收情形下回收渠道竞争对制造商最优联盟策略选择的影响;石纯来等[23]探讨了在单个回收商负责回收旧情形下奖惩机制对制造商合作策略的影响;黄宗盛等[24]在仅由零售商负责回收下构建了制造商成本分担和任务分担两种回收合作博弈模型以探讨回收合作模式选择问题;肖敏等[25]考虑回收商开展回收情形下,分析产能约束条件下回收率奖惩机制对制造商合作策略的影响;肖旦等[26]考虑由制造商、零售商和两个相互竞争的回收商组成的闭环供应链中构建了制造商与供应链成员的竞合博弈以分析不同情形下的最优竞合策略。
关于消费者回收行为的研究,LI等[27]考虑正规和非正规两种回收渠道各自特征,建立了Stackelberg博弈模型,分析消费者对正规回收渠道偏好对双回收渠道的影响;FENG等[28]考虑消费者对线上回收渠道存在偏好,分析了回收经销商通过自建网络回收渠道和回收者回收的最优决策问题;WANG等[29]探讨了消费者偏好第三方回收渠道对制造商、零售商和第三方组合回收下最优价格和利润决策的影响;许民利等[30]在考虑消费者环保意识的基础上,构建了基于不同消费者群体行为的双回收渠道模型以分析竞争情形与合作情形下供应链决策问题。另考虑消费者其他回收行为的探究,CHEN等[31]将消费者的个性特征与后悔心里引入到不同策略中,分析消费者在非正式和正式回收渠道之间的行为决策影响;HE等[32]考虑在制造商和零售商共同回收下消费者对制造商提供的网络回收渠道感到不便,分析制造商和零售商的最优回收投资和回收率决策问题;许民利等[33]从消费者对传统回收渠道和网络回收渠道的认可态度出发,探究了制造商、传统回收商和网络回收商的产品回收策略问题。
上述研究成果中关于竞争回收渠道的研究主要涉及制造商与零售商、制造商与第三方以及零售商和第三方竞争的回收情形,但考虑第三方回收下存在两个竞争回收商的研究较少。虽然部分文献考虑了制造商回收合作,但主要探讨制造商在单一回收渠道下的合作问题。只有少部分文献分析了制造商在双回收渠道下的合作策略问题。同时,消费者作为回收活动的主要参与者,对其回收行为的分析也显得尤为重要。基于此,本文对回收模式相异下消费者偏好对制造商合作策略的影响进行研究,以试图解决如下问题:①考虑传统回收与智能回收的差异性,在回收决策上将呈现怎样的特征?②竞争回收下,制造商该选择何种合作策略?不同合作策略对制造商、零售商和回收商会产生怎样的影响?③消费者对智能回收的选择偏好会对制造商的合作策略产生怎样的影响?本文根据传统回收与智能回收存在的差异,考虑消费者对智能回收的偏好,构建了制造商与传统回收商和智能回收商无合作、制造商仅与传统回收商合作、制造商仅与智能回收商合作以及制造商与传统回收商和智能回收商共同合作的决策模型,分析了不同合作情形下消费者的回收偏好对制造商和供应链其他成员的影响,以期为制造商和回收商的最优决策与合作策略的选择提供决策参考。
1 模型描述与假设
1.1 问题描述
本文以可再生资源回收(如废纸、废铁、塑料等旧产品)为例,分析传统回收和智能回收模式下的制造商合作策略。传统回收模式主要包括依靠个人拾荒者捡拾、小商贩走街串巷零散收购以及个体打包站回收等回收模式,本文将从事此类回收模式的经营者统称为传统回收商。而智能回收主要是指回收经营者依靠布局在社区、街道、居民楼等区域的智能回收设备实现消费者废旧物品的自主回收,在智能回收过程中,消费者需将废旧物品自主投递到智能回收箱以获得一定的产品回收报酬。由于传统回收商和智能回收商均需将回收的旧产品转售给制造商进行回收再制造,制造商可选择与回收商之间进行合作,共同决策旧产品的回收定价,以减少各自决策带来的双重边际化效应。
在闭环供应链中,制造商利用原材料或回收的废旧产品进行产品生产,并将新产品批发给零售商,零售商将其销售给消费者。消费者使用过产品后将废旧产品转卖给传统回收商或智能回收商以获取一定收益。传统回收商和智能回收商分别将回收的旧产品转售给制造商以获得利润。制造商与零售商、传统回收商和智能回收商进行Stackelberg博弈,在博弈决策中,制造商为供应链领导者,而零售商、传统回收商和智能回收商为追随者。其中,制造商先决策批发定价和转移定价,零售商决策产品零售价,传统回收商和智能回收商分别决策旧产品的回收定价,如图1所示。图1a为制造商与传统回收商和智能回收商无合作情形,图1b为制造商仅与传统回收商合作情形,图1c为制造商仅与智能回收商合作情形,图1d为制造商与传统回收商和智能回收商共同合作情形。

1.2 模型假设
为便于模型分析,参照已有研究文献[12-13,22,28],对竞争回收下制造商的合作策略研究变量定义如表1所示。

表1 相关参数定义
不失一般性,本文作出如下假设:
假设1a为产品市场潜在需求,pr为产品零售价,Dr为产品市场实际需求。其中:Dr=a-βpr,且需满足a>βpr。
假设2假设回收产品均为可再制造的,且回收产品的再制造成本相同,即不考虑回收产品质量的不确定性或差异性,且再制造产品与使用原材料生产的产品无差异。
假设3制造商使用原材料生产产品的成本为cm,使用旧产品的再制造成本为cr,制造商再制造节约成本为Δ=cm-cr。为了保证制造商参与旧产品再制造活动中,需满足条件Δ>0,即产品再制造的单位成本小于生产新产品的单位成本。
假设4考虑传统回收和智能回收在回收成本上存在差异,参考文献[34],假设智能回收的回收成本高于传统回收的回收成本,即cs>ct。
假设5假设旧产品总的市场规模为1。消费者对智能回收的选择偏好为θ,且θ∈(0,1)。θ越小,表明消费者对智能回收的选择偏好越小;θ越大,表明消费者对智能回收选择偏好越大。
假设6由于两种回收模式不同,环保意识高的消费者更愿意选择智能回收,降低对回收产品的预期价值。消费者认为旧产品回收环保处理需要额外的成本,且更愿意付出更多回收成本。本文假定消费者选择传统回收需要付出一定的成本,参考文献[27,32,35-36],假设消费者选择智能回收需额外付出一定的回收成本es。
1.3 回收函数


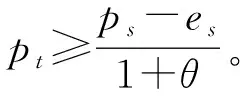
根据上文分析,有:
(1)
(2)
2 模型建立与求解
2.1 制造商与回收商无合作
在制造商与传统回收商和智能回收商无合作情形下,制造商、零售商、传统回收商和智能回收商为独立的决策者,各自决策旨在寻求自身利益最大化。其中,制造商先确定产品的批发价格和旧产品的转移价格(w,bt,bs),零售商再决策零售价格pr;最后,传统回收商和智能回收商分别决策回收定价(pt,ps)。其中,制造商、零售商、传统回收商和智能回收商的利润函数分别为:
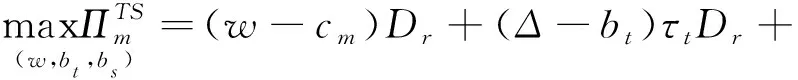
(3)
(4)
(5)
(6)
运用逆向归纳法求解,求解过程详见附录中第1部分,其最优结果如下:
制造商的最优批发价格和转移价格分别为:
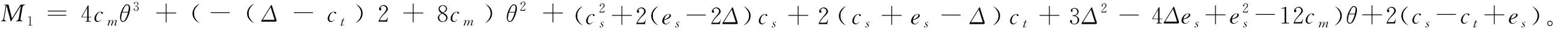
零售商的零售定价和市场需求为:
传统回收商和智能回收商的回收价格和回收率分别为:
传统回收商、智能回收商、零售商和制造商的利润分别为:

命题1当制造商与传统回收商和智能回收商无合作时,存在:
证明


命题1表明:在制造商与回收商无合作情形下,当消费者对智能回收的偏好保持在较小的阈值范围内,传统回收价格低于智能回收价格,传统回收率高于智能回收率,且传统回收商的利润高于智能回收商的利润;反之,则呈相反关系。因为对回收商来说,回收价格和回收率的大小直接决定其利润。在竞争回收下,若消费者对智能回收的选择偏好较小,直接导致智能回收率低,此时智能回收商只有提高回收价格吸引消费者选择智能回收。相反,当消费者对智能回收的偏好较大时,传统回收商需提高回收价格以吸引消费者选择传统回收,进而提高自身回收率和利润。
2.2 制造商与传统回收商合作
在制造商与传统回收商合作下,制造商和传统回收商以双方整体利润最大化为目标。其决策顺序为:制造商和传统回收商同时决策新产品的批发价和旧产品的回收价格以及给智能回收商的转移定价(w,bs,pt);然后,零售商确定产品的零售价pr;最后,智能回收商在决策其回收定价ps。此合作策略下决策问题转化为如下模型:

(7)
(8)
(9)
同理,运用逆向归纳法求解,求解过程见附录中第2部分,其最优结果如下:
制造商的最优批发价格和转移价格以及传统回收价格分别为:
其中M2=((Δ-ct)2-8cm)θ2+2(-Δ2+(cs+es)Δ-(-Δ+cs+es)ct+4cm)θ-(cs-ct+es)2。
零售商的零售定价和市场需求为:
传统回收商的回收率和智能回收商的回收价格和回收率分别为:
零售商和智能回收商的利润以及制造商和传统回收商合作后的总利润分别为:
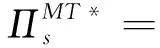
命题2当制造商与传统回收商合作时,存在:
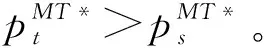
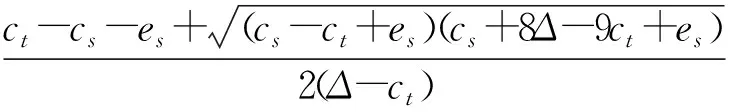
证明
(2)证明方法如命题1,此处不再赘述。
命题2表明:在制造商与传统回收商合作下,传统回收价格始终高于智能回收价格。这是因制造商与传统回收商合作时共同决策减少了制造商决策给传统回收商的转移价格环节,进而削减了双重边际效应,对提高传统回收价格有利。当消费者对智能回收的偏好保持在一定阈值范围内,传统回收率高于智能回收率;相反,当消费者对智能回收的偏好保持在较大阈值范围内,智能回收率高于传统回收率。因制造商与传统回收商合作,如消费者对智能回收的偏好较小,传统回收商在回收市场更具有优势。然而,当消费者对智能回收的偏好较大时,即使制造商与传统回收商合作,智能回收率也仍会高于传统回收率。
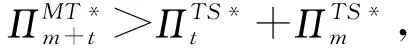
命题3表明:当制造商与传统回收商合作时,合作后的总利润高于两者在TS模型时获得的利润总和,且存在μm和μt使得制造商和传统回收商合作后各自获得的利润高于合作前的利润。其中,制造商和传统回收商合作后的利润分成比例系数大小需根据合作中双方议价能力来确定。
2.3 制造商与智能回收商合作
在制造商与智能回收商合作下,制造商和智能回收商以双方整体利润最大化为目标。其决策顺序为:制造商和智能回收商同时决策产品批发价和旧产品的回收价以及传统回收商的转移定价(w,bt,ps);然后,零售商确定产品的零售定价pr;最后,传统回收商在决策其回收定价pt。此合作策略下该决策问题转化为如下模型:

(10)
(11)
(12)
同理,运用逆向归纳法求解,求解过程见附录中第3部分,其最优结果如下:
制造商的批发价格和转移定价以及智能回收商的回收定价分别为:

零售商的零售定价和市场需求为:
传统回收商的回收价格和回收率以及智能回收商的回收率分别为:
零售商和传统回收商利润以及制造商和智能回收商合作后的总利润分别为:
命题4当制造商与智能回收商合作时,存在:
证明:
(2)证明过程如命题1,此处不再赘述。
命题4表明:当制造商与智能回收商合作时,智能回收价格始终高于传统回收价格。这是因为制造商与智能回收商合作减少了制造商决策给智能回收商的转移价格环节,削减了双重边际化效应,对智能回收商提高回收价格有利。当消费者对智能回收的偏好保持在较小阈值范围内,此时传统回收率高于智能回收率;反之,当消费者对智能回收的偏好保持在较大阈值范围内,智能回收率高于传统回收率。说明即使在制造商与智能回收商合作情形下,智能回收价格高于传统回收价格,但当消费者对智能回收的选择偏好较小时,仍会出现智能回收率低于传统回收率。这也表明只有当消费者对智能回收的偏好较大时,制造商与智能回收商合作才有利。


命题5表明:在制造商与智能回收商合作下,合作后的总利润高于两者在TS模型时获得利润的总和,且存在μm和μs使得制造商和智能回收商合作后各自获得的利润高于未合作之前的利润。其中,制造商和智能回收商各自的利润分成比例系数大小需根据合作中双方讨价还价的能力来确定。
2.4 制造商与传统回收商和智能回收商共同合作
当制造商与传统回收商和智能回收商共同合作,制造商和两个回收商以整体利润最大化为目标。其决策顺序为:制造商与传统回收商和智能回收商共同决策产品批发价和旧产品的回收价(w,pt,ps);然后,零售商确定产品的零售定价pr。该决策问题转化为如下模型:
(Δ-pt-ct)τtDr+(Δ-ps-cs)τsDr,
(13)
(14)
同理,运用逆向归纳法求解,求解过程见附录中第4部分,其最优结果如下:
制造商的最优批发价格以及传统回收商和智能回收商的回收定价为:
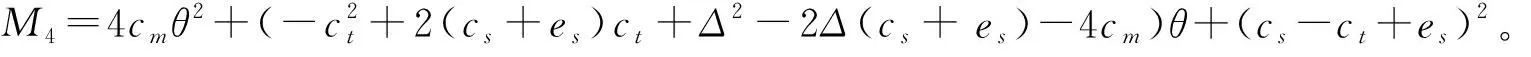
零售商的零售定价和市场需求为:
传统回收率和智能回收率分别为:
零售商的利润以及制造商、传统回收商和智能回收商三者合作后的总利润分别为:
命题6当制造商与传统回收商和智能回收商共同合作时,存在:
证明
(2)证明过程类似命题1,此处不再赘述。
命题6表明:在制造商与传统回收商和智能回收商共同合作下,传统回收价格高于智能回收价格。当消费者对智能回收的偏好保持在一定阈值范围内,智能回收商的回收率低于传统回收商回收率;反之,当消费者对智能回收的偏好超过阈值,传统回收商的回收率高于智能回收商的回收率。
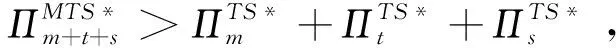
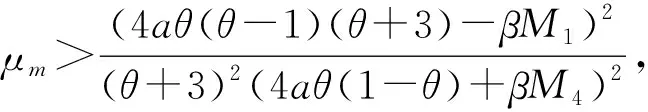
命题7表明:当制造商与传统回收商和智能回收商共同合作时,合作后的总利润高于三者在TS模型中获得的利润总和,且存在μm、μt和μs使得制造商、传统回收商和智能回收商合作后各自获得的利润均高于未合作之前的利润。其中,制造商、传统回收商和智能回收商各自的利润分成比例系数大小需根据合作三方讨价还价的能力来确定。
3 不同合作策略下的对比分析

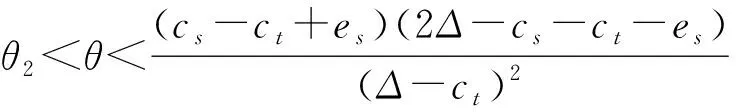
命题8表明:当制造商与传统回收商和智能回收商均无合作时,产品批发价格和零售价格最高,市场需求最低;相反,当制造商与传统回收商和智能回收商共同合作时,产品批发价和零售价最低,市场需求最高。当消费者对智能回收的偏好保持在一定阈值范围内,制造商与智能回收商合作时产品的批发价和零售价高于制造商与传统回收商合作情形,但市场需求低于制造商与传统回收商合作情形;反之,则呈相反关系。综合而言,相对于制造商无合作而言,制造商与回收商合作对降低批发价和零售价、增加市场需求有利;其中,制造商与传统回收商和智能回收商共同合作对降低批发价格和零售价格、增加市场需求更有利。

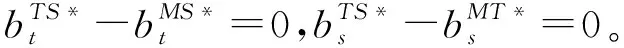
命题9表明:制造商与回收商无合作以及制造商与智能回收商合作时,制造商决策给传统回收商的转移价格相等。类似地,制造商与回收商无合作时以及制造商与传统回收商合作时,制造商决策给智能回收商的转移价格相等。这是因为竞争回收下,当制造商与其中一个回收商合作时,不变动另一回收商的转移价格,以减少因转移价格的变动引起的波动效应。
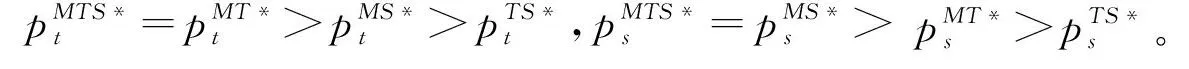
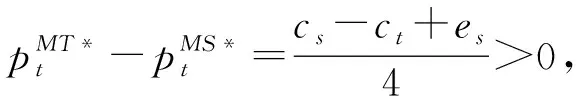
命题10表明:制造商与回收商无合作时传统回收商的回收价格最低。制造商与传统回收商合作以及制造商与传统回收商和智能回收商共同合作时传统回收商的回收价格最高且相等。同样地,制造商与回收商无合作情形下智能回收商的回收价格最低。制造商与智能回收商合作以及制造商与传统回收商和智能回收商共同合作时智能回收商的回收价格最高且相等。因制造商与回收商之间合作决策,能减少了制造商决策中间转移定价环节,从而减少双方各自决策产生的双重边际化效应,对回收商提高回收定价有利。
命题11不同合作策略下传统回收商、智能回收商和供应链的总回收率满足关系:

命题11表明:当制造商与传统回收商合作时,传统回收率最高。然而,当制造商与智能回收商合作时,传统回收率最低。当制造商与传统回收商和智能回收商共同合作时,当消费者对智能回收的偏好保持在一定阈值范围内,传统回收率高于制造商无合作时传统回收率;反之,则呈相反关系。同样地,当制造商与智能回收商合作时,智能回收率能够达到最高。然而,当制造商与传统回收商合作时,智能回收商的回收率最低。当消费者对智能回收渠道的偏好保持在一定阈值范围内,制造商无合作时智能回收率高于制造商与传统回收商和智能回收商共同合作时的智能回收率;反之,则呈相反关系。另外,当制造商与智能回收商合作时供应链的总回收率与制造商与传统回收商和智能回收商共同合作时供应链的总回收率相等且达到最高。当制造商无合作时供应链的总回收率最低。综合表明,在竞争回收下制造商与其中一个回收商合作,能够增加合作回收商的回收率,而未参与合作的回收商其回收率将会降低。其中,制造商与传统回收商和智能回收商共同合作对增加供应链的总回收率有利。

命题12表明:相对于制造商与回收商无合作情形,如制造商与传统回收商合作,智能回收商的利润会受损。同样地,当制造商与智能回收商合作时,传统回收商的利润会减少。这表明在竞争回收下,如制造商如与其中一个回收商合作,另一个回收商的回收利润会受损。
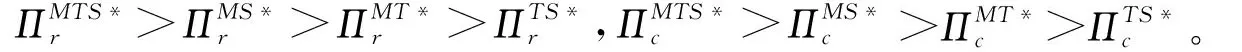
命题13表明:制造商与传统回收商和智能回收商共同合作下零售商和供应链的总利润达到最高,制造商与传统回收商和智能回收商无合作时零售商和供应链的总利润最低。其中,制造商与智能回收商合作下零售商和供应链的总利润高于制造商与传统回收商合作。制造商与传统回收商和智能回收商合作能够减少供应链关系中不确定性因素,合作成员发挥各自优势,提升竞争力。
4 算例分析
为进一步验证上述模型与结论的正确性,对各最优决策进行数值分析,进而得到新的管理见解。在满足假设条件下,结合实际情形对模型中参数赋值如下:a=500,β=0.3,cm=2.5,Δ=1.2,ct=0.12,cs=0.15,es=0.02,上述参数赋值均满足不同合作策略下Hessian矩阵凹性判定条件。根据参数设置,不同合作策略下参数θ均需满足θ>0.046,相关分析结果如图2~图8和表2所示。
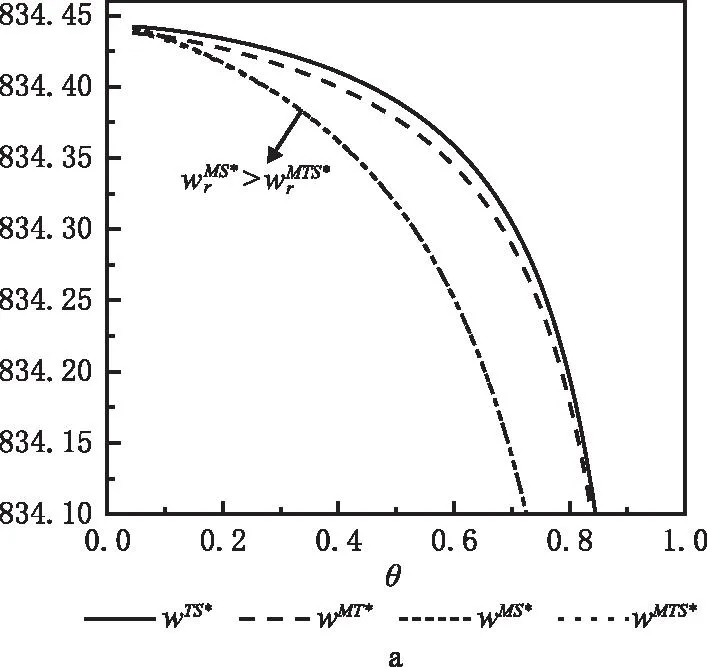
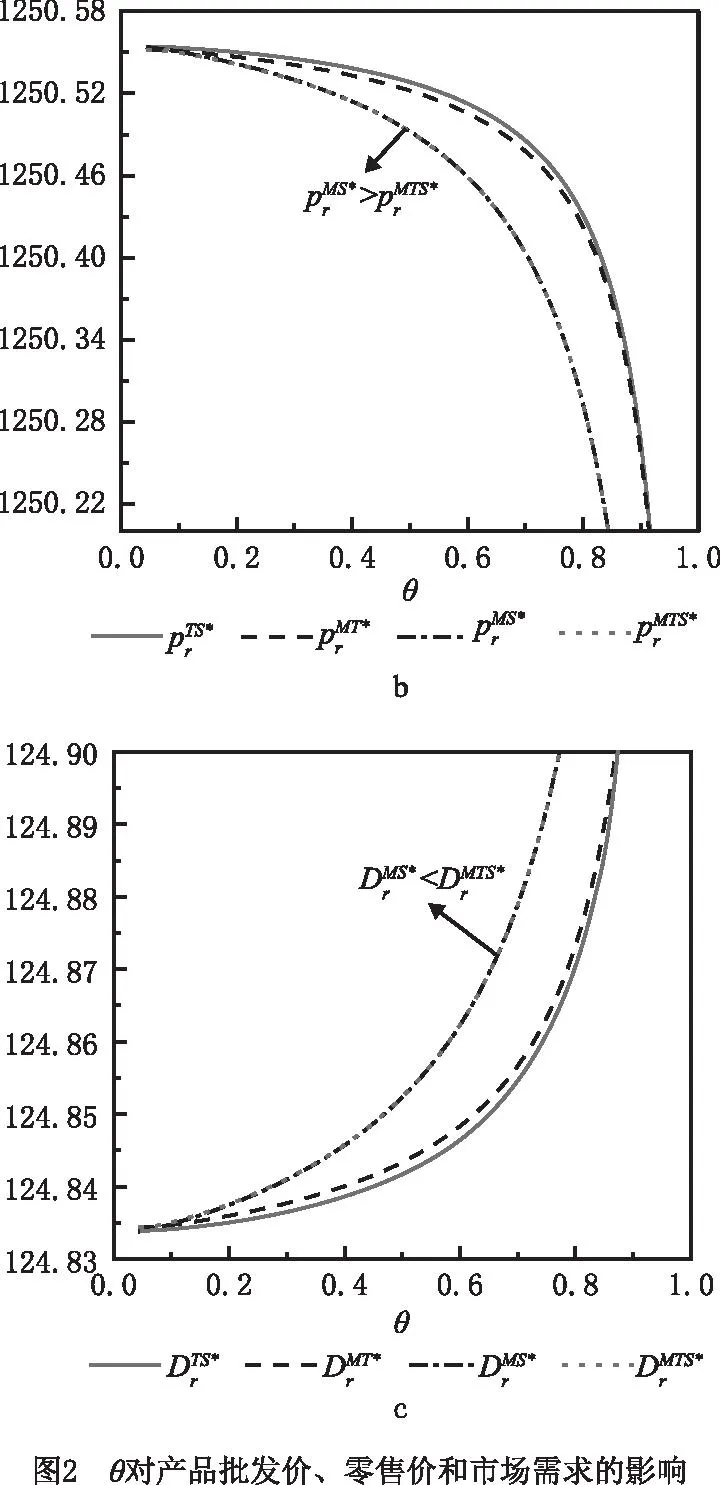
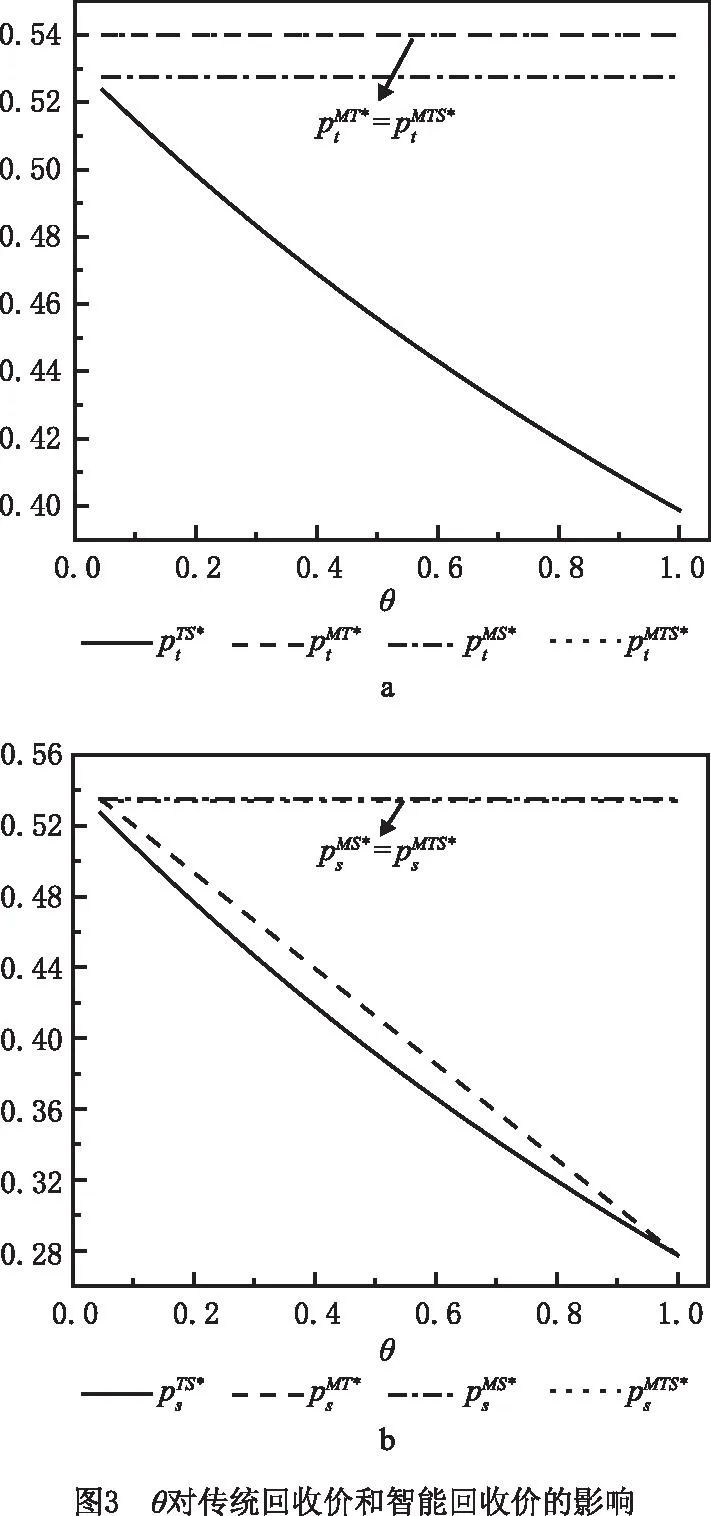

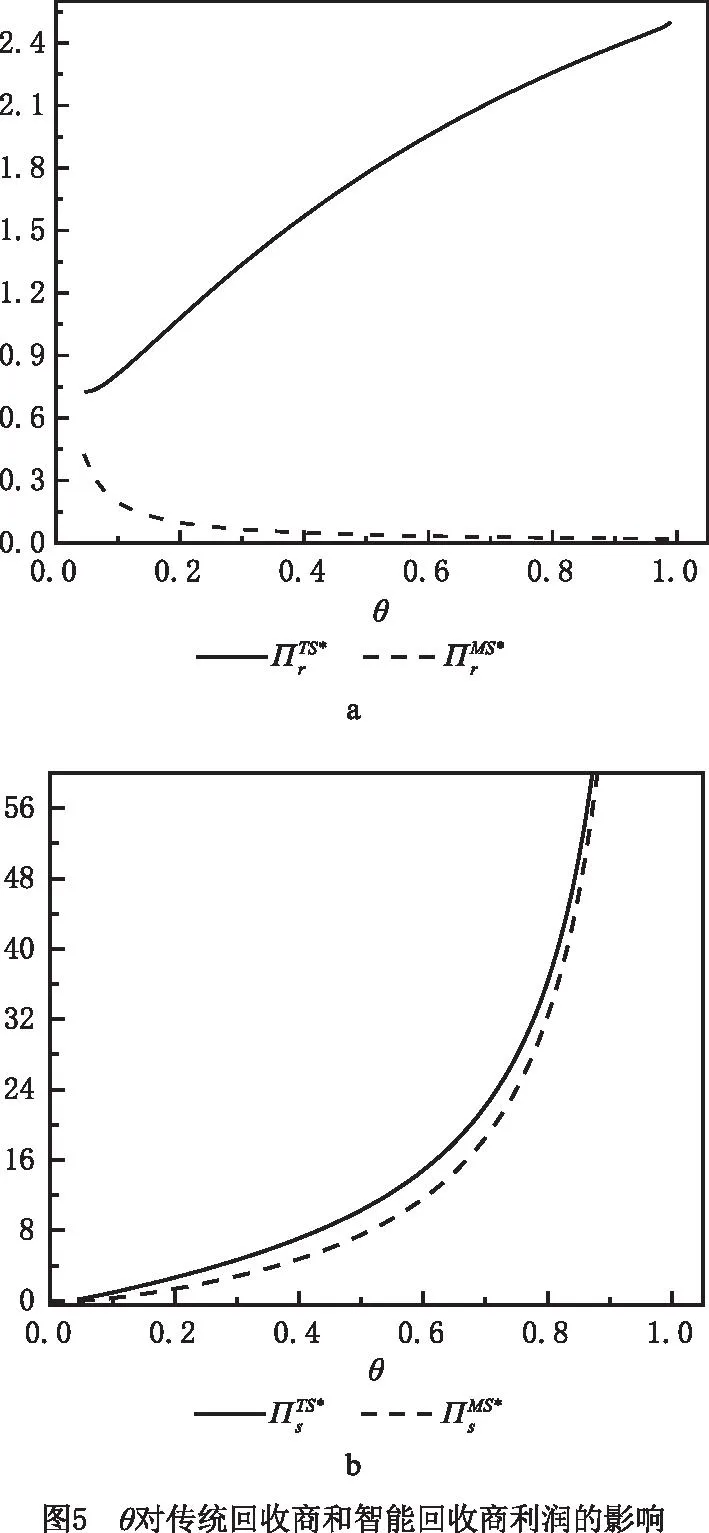
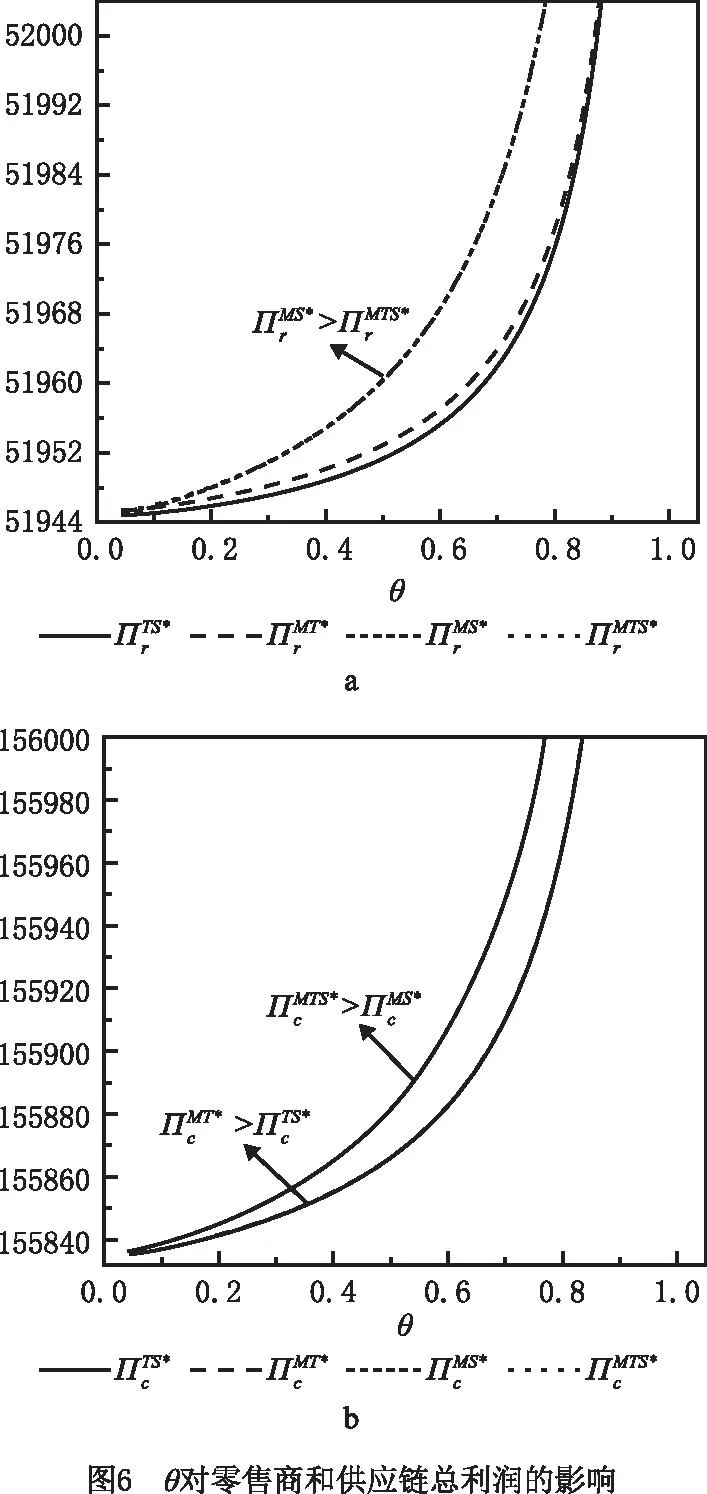
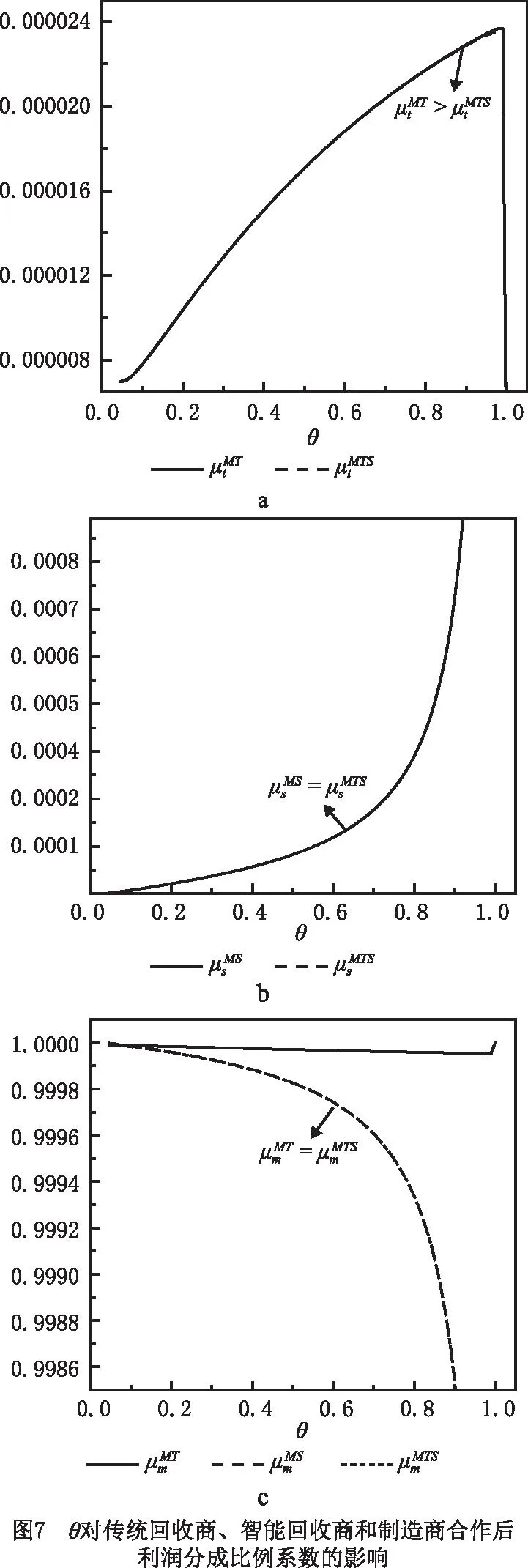

表2 θ对合作前后合作成员利润的影响
(1)参数θ对批发价、零售价和市场需求的影响
从图2a~图2c可知,随着消费者对智能回收渠道偏好的增加,产品批发价格和零售价格逐渐降低,而产品市场需求逐渐增加。不同合作策略下产品批发价格和零售价格的大小关系保持一致,与市场需求呈相反关系。无合作策略TS下产品批发价和零售价最高,市场需求最低。在合作策略MTS中产品批发价格和零售价格最低,产品市场需求最高。当消费者对智能回收渠道的偏好保持在一定阈值范围内,合作策略MT中产品批发价格和零售价格高于合作策略MT;反之,则呈相反关系。消费者对智能回收偏好增加,侧面反应消费者环保意识增强,更愿意实施回收,这对增加产品回收量有利,进而能够降低产品生产成本,降低批发价格和零售价格,增强市场需求。
(2)参数θ对回收价格和回收率的影响
从图3a可知,合作策略MT和MTS中传统回收商的回收价格一致,且达到最高。合作策略MS中传统回收价高于无合作策略TS中传统回收价。从图3b可知,合作策略MS和MTS中智能回收价相等,且达到最高。合作策略MS中智能回收价始终高于无合作策略TS和合作策略MT中智能回收价。由图3可知,当消费者对智能回收偏好的增加,传统回收价和智能回收价均会呈下降趋势。说明当消费者对智能回收的偏好增加,智能回收商可降低回收价格。随智能回收价格的降低,传统回收商的回收定价也会随智能回收定价的降低而降低。
从图4a可知,合作策略MT中传统回收率始终高于无合作策略TS和合作策略MS、MTS中传统回收率,而合作策略MS中传统回收率最低。当消费者对智能回收的偏好保持在一定阈值范围内,合作策略MTS中传统回收率高于无合作策略TS中传统回收率;反之,则呈相反关系。从图4b可知,合作策略MS中智能回收率最高,合作策略MT中智能回收率最低。当消费者对智能回收的偏好保持在一定阈值范围内,无合作策略TS中智能回收率高于合作策略MTS中智能回收率;反之,则呈相反关系。从图4c可知,无合作策略TS中供应链的总回收率最低,合作策略MS和MTS中供应链的总回收率最高且相等。综合图4可知,随消费者对智能回收的偏好增加,不同合作策略下传统回收率逐渐下降,智能回收率和供应链的总回收率均呈上升趋势。制造商与回收商合作能够增加回收商的回收率和供应链的总回收率,这对制造商降低生产成本有利。
(3)参数θ对回收商、零售商和供应链总利润的影响
由图5a可知,在无合作策略TS中,随着消费者对智能回收偏好的增加,传统回收商的利润呈先下降后增长趋势变化;在合作策略MS中,传统回收商的利润随消费者对智能回收偏好的增加而逐渐下降;在无合作策略TS和合作策略MT中,智能回收商的利润随消费者对智能回收偏好的增加而增长。综合图5a和图5b可知,在合作策略MT中,智能回收商的利润低于无合作策略TS情形。同样,对比合作策略MS,在无合作策略TS中传统回收商的利润会降低。说明在竞争回收下,制造商与回收商合作能够提高合作后的整体利润,而未参与到合作的回收商,其利润将会受损。如合作策略MT中,制造商和传统回收商合作减少了制造商决策给传统回收商转移价格的中间环节,进而降低双重边际效应带来的负面影响,这对提升制造商和传统回收商的利润有利。然而,对智能回收商来说,因合作策略MT中制造商始终保持给智能回收商的转移价格不变,此情形下智能回收价格又低于传统回收价格,对比之下智能回收价格无竞争优势,难以吸引消费者,导致其回收量降低,回收利润减少。
从图6a可知,在合作策略MS中零售商的总利润最高,无合作策略TS中零售商的总利润最低。其中,合作策略MTS中零售商的总利润高于合作策略MT下零售商取得的总利润。表明制造商与回收商合作,虽零售商未参与到合作中,但也能从合作中间接受益。这是因制造商与回收商合作,增加了总回收量,降低了生产成本,能够减少产品批发价格与零售价格,增加市场需求,为此零售商能够从中获得更多利润。从图6b可知,合作策略MTS中供应链的总利润达到最高,无合作策略TS中供应链的总利润最低。同时,合作策略MS中供应链的总利润高于合作策略MT中供应链的总利润。综合图6a和图6b可知,随消费者对智能回收偏好的增加,零售商和供应链的总利润均会逐渐增加。其原因是零售商和供应链的总利润大小的变化受产品回收率、生产成本以及市场需求波动的影响。
(4)参数θ对合作前后合作成员利润的影响
从图7a~图7c可知,随消费者对智能回收的偏好逐渐增加,传统回收商和智能回收商合作后的利润分成比例系数逐渐增大,而制造商合作后的利润分成比例系数呈下降趋势。说明消费者对智能回收偏好越大,传统回收商和智能回收商在回收合作后的利润分成比例的议价能力越大,而制造商在回收合作后利润分成比例的议价能力越小。其中,智能回收商合作后的利润分成比例系数受消费者对智能回收的偏好影响波动较小,传统回收商和制造商合作后的利润分成比例系数受消费者对智能回收的偏好影响波动较大。
由表2和图8a~图8c可知,相对于无合作策略TS情形,合作策略MT、MS和MTS中制造商与传统回收商和智能回收商合作后的总利润均高于无合作策略TS情形下制造商与传统回收商和智能回收商各自决策时的利润总和。从表2和图8d可知,当消费者对智能回收的偏好保持在较小阈值范围内,合作策略MT和MTS中合作后增长的利润高于合作策略MS。反之,当消费者对智能回收的偏好保持在一定阈值范围内,合作策略MS中合作后增长的利润高于合作策略MT和MTS。
5 结束语
本文分析了回收模式相异下消费者偏好对制造商合作策略的影响。考虑消费者对智能回收的偏好,分别构建了制造商与传统回收商和智能回收商无合作、制造商仅与传统回收商合作、制造商仅与智能回收商合作以及制造商与传统回收商和智能回收商共同合作的决策模型,应用Stackelberg博弈理论与逆向归纳法求解不同合作策略下供应链各成员的最优决策,并进行对比分析与算例分析,以解析消费者对智能回收的偏好对不同合作策略下供应链各成员决策的影响。
研究表明:①相对于制造商与传统回收商和智能回收商无合作情形,制造商采取合作策略能够降低产品批发价格与零售价格,提高市场需求。其中,合作策略MTS对降低产品批发价格和零售价格,提高产品市场需求更有利。②与其他合作策略相比,无合作策略TS中传统回收价格和智能回收价格均最低。合作策略MT和MTS中,传统回收价格最高且相等;合作策略MS和MTS中,智能回收价格最高且相等。③相较于制造商与传统回收商和智能回收商无合作,制造商与回收商合作对合作参与的回收商增加回收率有利,此时未参与合作的回收商的回收率会减少。如合作策略MT对增加传统回收商的回收率最有利,而此时智能回收商的回收率最低;相反,合作策略MS中智能回收商的回收率最高,而此时传统回收商的回收率最低。④制造商与传统回收商和智能回收商均有合作动机,且合作后各自的利润均高于未合作前的利润。当消费者对智能回收的偏好保持在一定阈值范围内,制造商与智能回收商合作后增长的利润高于合作策略MT和MTS。其中,合作策略MT中制造商与传统回收商合作后增长的利润最少。此外,与制造商无合作情形相比,合作策略下零售商和供应链的总利润也得到提高。⑤制造商合作后利润分成比例的大小与消费者对智能回收的偏好大小有关。随消费者对智能回收偏好的增加,传统回收商和智能回收商在合作后的利润分配系数逐渐增大,制造商在合作后的利润分配系数逐渐减少。说明消费者对智能回收偏好的增加,能提升传统回收商和智能回收商在合作后的利润分配议价能力,但会降低制造商在合作后的利润分配议价能力。
上述研究结论对闭环供应链成员的管理决策具有如下启示:
(1)智能回收新模式突破了原有传统人工回收的垄断市场,拓宽了制造商废旧品回收渠道,特别是废纸、塑料、饮料品等回收,但也会造成回收商之间的竞争。从合作后增长的利润大小角度看,制造商与智能回收商合作更能提升自身利润。
(2)由于传统回收与智能回收在回收方式与日常运营上都存在差异,加上消费者对不同回收模式存在选择偏好,回收商之间可发挥各自回收方式优势,增加回收量,以提高自身利润。
(3)制造商作为回收再制造的下游企业,增加回收量对降低生产成本和履行企业社会责任启到积极作用,制造商可利用回收合作以减少单个决策带来的边际负面效应,促进合作联盟以提升供应链绩效。
本文在竞争回收下考虑消费者对智能回收的偏好分析了制造商不同合作策略中的决策问题,然而针对传统回收与智能回收之间竞争,制造商如何发挥其供应链的领导作用,协调回收商之间的竞争,减少回收渠道冲突还有待探究。同时,本文仅考虑传统回收与智能回收的竞争,实际中回收活动往往存在同一类型多个回收商之间同质竞争,进一步研究可考虑此情形下制造商的合作问题。
附录
1 TS模型的求解过程
运用逆向求解法求解。对正文中式(5)和式(6)分别求关于pt和ps的一阶和二阶偏导,有:



2 MT模型的求解过程
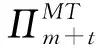


3 MS模型的求解过程
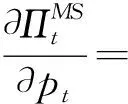
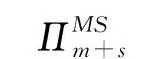
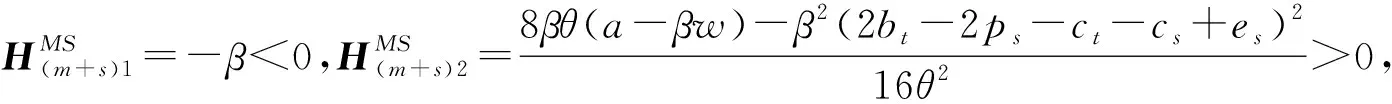

4 MTS模型的求解过程
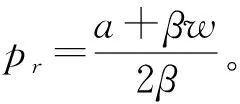


5 命题3、命题5和命题7的证明过程
命题3证明
命题5证明:
命题7证明:
6 命题8的证明过程
证明
7 命题11的证明过程
证明:
8 命题12的证明过程
证明:
+(cs-ct+es)2)β)+8(θΔ-(1+θ)ct+cs+es)2(4aθ(θ-1)(θ+3)+(-4cmθ3+((Δ-ct)-8cm))θ2
(θ+3)3((Δ-ct)θ-cs+ct-es)2((((Δ-ct)2-8cm)θ2+2((Δ-cs-es)ctΔ2(cs+es)Δ+4cs)θ-
(cs-ct-es)2))β+8aθ(θ-1))+8((5Δ-cs-ct-es)θ-cs+ct-es)2(4cmθ3+(-(Δ-ct)2+8cm)θ2+(2(cs
9 命题13的证明过程
证明:
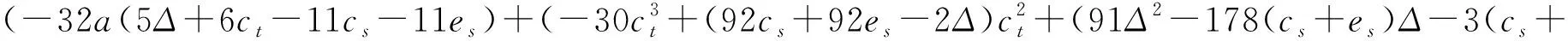
es)2+192cm)ct-59Δ3+(86cs+es)Δ2+3(cs+es)2+160cm)Δ-352cm(cs+es))β)θ3+32a(3Δ-4ct+

