考虑双积分和碳交易背景下基于最优控制的新能源汽车生产决策分析

刘春玲,赵利利,黎继子,高梦圆,邓旭东

(1.武汉纺织大学 机械与自动化学院,湖北 武汉 430070;2.湖北省数字化纺织装备重点实验室,湖北 武汉 430073;3.武汉科技大学 恒大管理学院,湖北 武汉 430081)

0 引言

国内汽车行业近十多年的飞速发展使得中国成为世界最大的汽车生产国和消费国。但是传统汽车带来的环境污染也很突出,从汽车中排放出来的尾气严重污染大气,影响空气质量,释放的二氧化碳等温室气体使得全球气候变暖。这一系列环境问题迫使汽车行业做出改变,于是新能源汽车应运而生,由于新能源汽车行业处于发展的初级阶段,技术不是很完善,价格较高,市场需求仍然不稳定。故此,为了推动新能源汽车市场,各个国家出台了相应的激励政策和措施,如美国在2006年通过建立和完善法律法规,设立政府资助项目用于新能源汽车及部件的研发,通过优惠税收和补贴的方式系统地促进新能源汽车产业的发展;日本在2009年实施绿色税制,对购买新能源汽车的消费者免除多项税收来鼓励新能源汽车产业发展;同年英国也通过免征收电动汽车交通拥堵费以及设立低排放区,来促进电动汽车的发展;特别是欧盟在2021年采取制定新能源汽车的共同标准、建立面向欧盟内部的充电站和促进新能源电动汽车的开发和回收等一系列措施,以支持新能源汽车的发展。

中国作为新能源汽车产销第一大国,除了提供新能源汽车生产购置补贴和免征购置税外,也建立一系列国家层面的新能源汽车推广机制,如提升高速公路服务区和公共停车位的快速充电换电覆盖率,大大推动了新能源汽车的发展。2020年新能源汽车销售量达136.7万辆,相比2019年增长10.9%。但在政策补贴方式下,也带来了一系列的问题,比如很多企业在生产新能源汽车中,只注重生产数量而忽略质量,只注重拿政府补贴而忽视技术水平的提高。同时由于补贴政策,政府也承担较大的财政压力。为了新能源汽车行业可持续发展,提高企业技术竞争力,在2018年国家颁布了新能源汽车“双积分”生产政策,这一政策的实施,改变了汽车制造商外部环境,意味着新能源汽车产业由原来政府驱动变为市场驱动。所谓“双积分”是指传统燃油车平均燃油消耗量积分和新能源汽车积分。在该政策中,不仅要求传统汽车制造商生产的燃油车燃油消耗量达标且逐年下降,而且还需积累或购买一定新能源汽车积分,满足这两个条件后,则该燃油车型方可生产。当然,新能源汽车积分需要新能源汽车企业所制造的新能源汽车必须达到一定质量标准,才能计算新能源汽车积分,且该积分可用来交易,可卖给一些传统燃油汽车制造商,用于其生产传统燃油车的先决条件,以及抵减燃油车燃油消耗不达标的情形。

目前国内外学者对“双积分”政策背景下新能源汽车的研究,主要聚焦在补贴政策和双积分政策对比性分析以及有效性检验上[1]。如李旭等[2]从显著性、敏感性和稳定性3个维度,分析了“双积分”政策影响下新能源汽车环境绩效和经营绩效的动态变化特征;LI等[3]利用博弈论模型分析了传统燃油汽车和新能源汽车在双积分政策的有效性,研究表明双积分政策相比较补贴政策而言,能够使新能源汽车数量提高至在补贴政策环境下的两倍;程永伟等[4]研究了“双积分制”下汽车生产商生产决策问题,建立新能源汽车与传统燃油汽车联合决策模型,分别针对在积分剩余、积分不足和积分平衡三种情况下,求解最优定价和最优产量;于晓辉等[5]则通过建立整车厂和汽车零部件供应商组成的两级供应链动态博弈模型,来研究在纯电动汽车“双积分”政策下如何提高电动汽车的质量和双方利润;LUO等[6]建立了双积分政策下传统燃油车和新能源汽车生产优化的决策模型,研究发现当汽车制造商的新能源汽车年末积分没有达标时,“双积分”政策将不利于新能源汽车的生产,反而增加了传统燃油车的数量;LI等[7]通过建立多周期市场动态模型分析减速增长、加速增长、持续增长和固定百分比基准这四种情景下汽车制造商的产量、积分和利润的变化。上述这些文献中均没有考虑碳排放和碳交易因素,但不管是生产传统燃油车还是新能源汽车,在生产过程中必然产生碳排放,带来温室气体的增加[8-9]。因此,碳排放和碳交易因素是汽车行业未来生产决策遇到的另一个焦点。

在涉及到碳交易的新能源汽车生产分析的文献中,袁琦等[10]通过构建企业生产决策模型,研究了在新能源汽车碳配额体系下,企业生产决策与碳配额份额的影响,表明政府将新能源汽车纳入碳配额体系进行碳配额调控,有利于企业生产更多的新能源汽车;李文翔等[11]构建了基于多智能体碳交易仿真模型,对引入碳交易机制下的新能源汽车发展路径进行仿真预测,发现引入道路交通碳交易机制能够有效促进新能源汽车跨越式发展;王松澔[12]站在碳减排角度,建立系统动力学模型,从国家和市场共同调控下进行仿真,对于新能源汽车推广方式进行灵敏度分析,测算出新能源汽车减排量;汪挺松等[13]通过构建消费者购车决策模型,对传统燃油车和新能源汽车进行分析,得出均衡碳交易价格,研究发现若市场碳价期望值比均衡碳交易价格高,则消费者更倾向于购买新能源汽车;程永伟等[14]通过建立碳交易机制下传统燃油车与新能源汽车的联合生产决策模型,分别分析了碳交易对新能源汽车产量、价格和利润的影响,在碳配额交易量受限制和不受限制情形下,分析了碳价格波动下生产计划的鲁棒区间。

上述文献在分析新能源汽车生产的碳交易中,没有将双积分政策考虑其中,特别是没有从动态多周期的角度,分析碳交易和双积分政策下对新能源汽车生产的长期影响。一方面,碳交易政策是从企业绿色生产角度出发来,促进企业改善生产过程和生产工艺,而双积分政策是从产品角度,促进汽车行业从传统的燃油汽车转向生产绿色的新能源汽车,特别是高质量的新能源汽车,故此,对于碳交易政策和双积分政策,缺少任何一项政策,都不能全面反映汽车企业的绿色低碳生产决策问题;另一方面,从长期来看,由于企业生产产量必然是波动变化的,这就导致其对应所产生的新能源积分量和碳排放量也会发生变化,如果从静态来分析,则不能真实反映出新能源汽车企业随时间变化的最优决策的有效性和可行性。为此,本文将双积分和碳交易结合,利用最优控制理论对新能源汽车生产进行动态优化,分析在双积分政策和碳交易下的新能源汽车生产多周期动态决策问题。

1 模型建立

本文先建立一个基础模型,该模型是没有考虑双积分政策和碳交易政策背景下,新能源汽车企业的生产最优控制模型;在此基础上,分别建立了只考虑双积分政策条件下新能源汽车企业基于最优控制的生产模型--模型(Ⅰ)和同时考虑双积分和碳交易政策条件下新能源汽车企业基于最优控制的生产模型--模型(Ⅱ)。其中本文主要符号和含义如表1所示。

表1 主要的符号和含义

1.1 问题描述

假设有一新能源汽车生产商,在t周期内生产量为R(t),且在t周期的市场需求为D(t),则新能源汽车生产商库存为S(t),且设S(t)≥0,它表示t周期库存状态非负,那么该新能源汽车生产企业库存水平的状态方程可表示为:

(1)

假设新能源汽车生产厂商拥有的初始库存数量为S(0)=S0,C(R(t))表示t周期生产成本函数,该函数为非递减、非负的严格凸函数,那么该新能源汽车生产问题可通过Arrow-Karlin模型来表示:

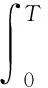
(2)

s.t.

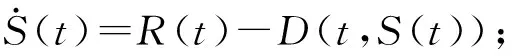
(3)

式(2)为目标函数,使得在计划期[0,T]中库存持有成本和生产成本之和最小。其中,生产量R(t)为控制变量,库存量S(t)为状态变量。

1.2 只有双积分政策下的生产决策模型-模型(Ⅰ)

考虑到在双积分政策下,该新能源汽车生产企业生产出每一辆新能源汽车,能产生一定的新能源汽车积分,该积分可以通过市场交易,卖给需要这些积分的传统燃油汽车制造商,因为这些传统燃油车制造商要想生产传统燃油车,必须购买一定量新能源汽车积分才能生产。故该政策通过这种机制设计,来促进和激励新能源汽车生产商,同时抑制传统燃油车的生产和销售。假设P(t)表示在t周期每单位新能源汽车积分的市场价格,n表示每一辆新能源汽车汽车平均转化为积分的比例,则t周期下生产R(t)辆新能源汽车的积分为nR(t),假设所有积分都能卖出去,并为该企业带来相应的收益,则在双积分政策下的该企业的生产决策模型(Ⅰ)可表示为:

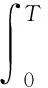
nR(t)P(t)]dt。

(4)

s.t.

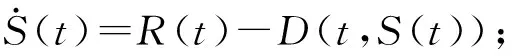
(5)

1.3 碳交易和双积分政策下的生产决策模型-模型(Ⅱ)

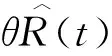
(6)

(7)

2 模型求解

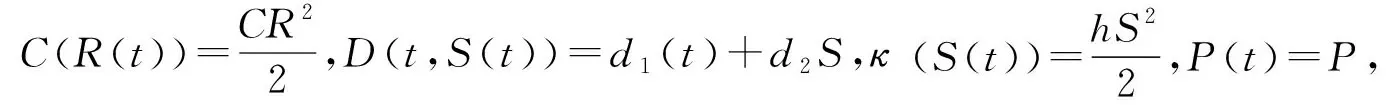
证明基于双积分政策下的生产决策模型是一个动态问题。根据庞特里亚最大值原理,由式(4)和式(5)构造成Hamilton函数:

H(t,S,R,λ)=-e-ρt{κ(S(t))+C(R(t))-
nR(t)P(t)]}+λ[R(t)-D(t,S(t))]。

(8)

为了得到双积分政策下的最优生产决策,必要条件是对(8)建立拉格朗日函数:

L(t,S,R,λ,μ)=-e-ρt{κ(S(t))+C(R(t))-
nR(t)P(t)}+λ[R(t)-D(t,S(t))]+
μ[R(t)-D(t,S(t))]。

(9)

式中:λ(t)为伴随函数;μ(t)为拉格朗日乘子函数。式(9)最大化的一阶必要条件分别为:

H(t,Sb,Rb,λ)≥H(t,S,Rb,λ),

(10)

(11)

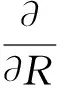
(12)

I(0)=I0,λ(T)=β,

(13)

R(t)-D(t,S(t))≥0,μ(t)≥0,

(14)

μ(t)[R(t)-D(t,S(t))]=0。

(15)

最优生产决策横截条件为:

(16)

将方程(11)和(12)化简得:

(17)

(18)

根据方程(14),有如下两种库存情况需要考虑:R(t)-D(t,S(t))=0和R(t)-D(t,S(t))>0。

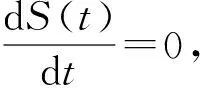
R*(t)=D(t,S*(t))。

(19)

将方程(18)带入(17)中得:

(20)

在上述方程的求解中,得到了伴随函数λ(t)以及常数β的表现形式,同时由方程(18)得到了拉格朗日乘子函数μ(t)的表现形式。值得注意的是,得到的μ(t)若是非负的,则方程(19)的解不可使用,即不存在最优生产决策。

情况2在[0,T]时刻内的某些子集中,当R(t)-D(t,S(t))>0时,即生产大于需求,产生了库存。此时μ(t)=0,那么在这种情况下,方程(12)、(17)和(18)等价于

将上述方程结合,得到二阶微分方程:

(21)

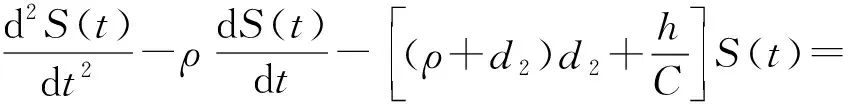
S(0)=S0,S(T)=ST。

(22)

则模型(I)的最优解,即新能源汽车企业的最优生产和库存水平为:

S*(t)=A1er1t+A2er2t+Q(t),

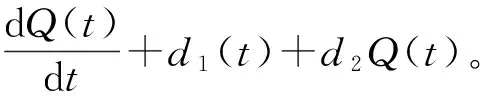
(23)

其中:

U(t)=-Csin(t)-C[(ρ+d2)sin(t)]+(θ+h)Pn。

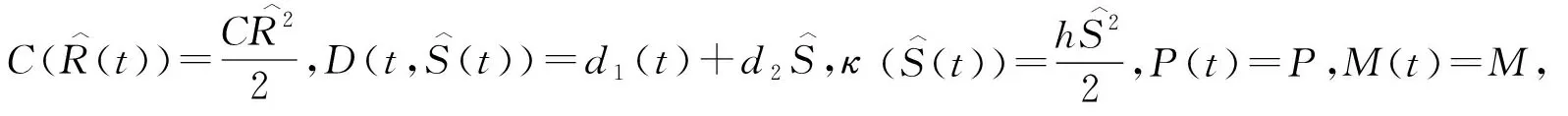
证明基于碳交易和双积分政策下的生产决策模型是一个动态多周期控制问题,同理根据庞特里亚金最大值原理原理,对式(6)和式(7)构造成Hamilton函数。

(24)

为了得到式(24)的必要条件和新能源汽车企业的最优解,建立相应的拉格朗日函数:

(25)

式中:λ(t)为伴随函数;μ(t)为拉格朗日乘子函数。

根据Hamilton最大值原理,函数(25)有最优解的必要条件为:

(26)

(27)

(28)

I(0)=I0,λ(T)=β,

(29)

(30)

(31)

相应的横截条件为:

方程(27)和(28)化简得:

(32)

(33)

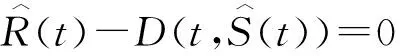
(34)

把方程(33)带入到方程(32)中得:

(35)

在上述方程的求解中,得到了伴随函数λ(t)以及常数β的表现形式,同时由方程(34)得到了拉格朗日乘子函数μ(t)的表现形式。在这里要得到的μ(t)若不是非负的,则方程(35)的解就不可使用,即不存在最优生产决策。

将上述方程结合,得到二阶微分方程:

(36)

为了方便计算,我们假设

其中C,h,d2为常数。

模型(Ⅱ)的最优解,即新能源汽车企业最优生产和库存的必要条件为:

(37)

由此得模型(Ⅱ)的最优的库存和生产量为:

B1(r1+d2)er1t+B2(r2+d2)er2t。

(38)

其中:

。

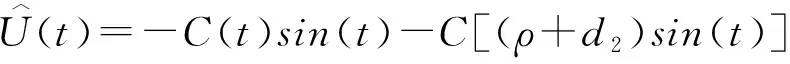
3 数值分析

为进一步分析不同情况下双积分和碳交易政策对新能源汽车生产的影响,在模型Arrow-Karlin模型、模型(Ⅰ)和(Ⅱ)中,结合LI等[7]的研究和东风新能源汽车有限公司的实际,设新能源汽车初始库存水平为S(0)=1.0(千辆),计划期T=12(月),D(t)=(1+0.05t)(1+sin(t)),C(R(t))=8R2(t)。为了简便起见,我们在数值分析中忽略风险折现系数。则Arrow-Karlin模型如下:

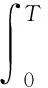
s.t.

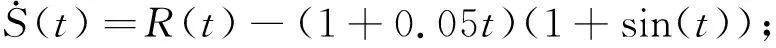
(39)

在模型(Ⅰ)中,假设单位新能源汽车积分价格P(t)=4(千元),新能源汽车数量和新能源积分换算比例n=0.3,保持其他参数不变。那么模型如下:

s.t.

(40)

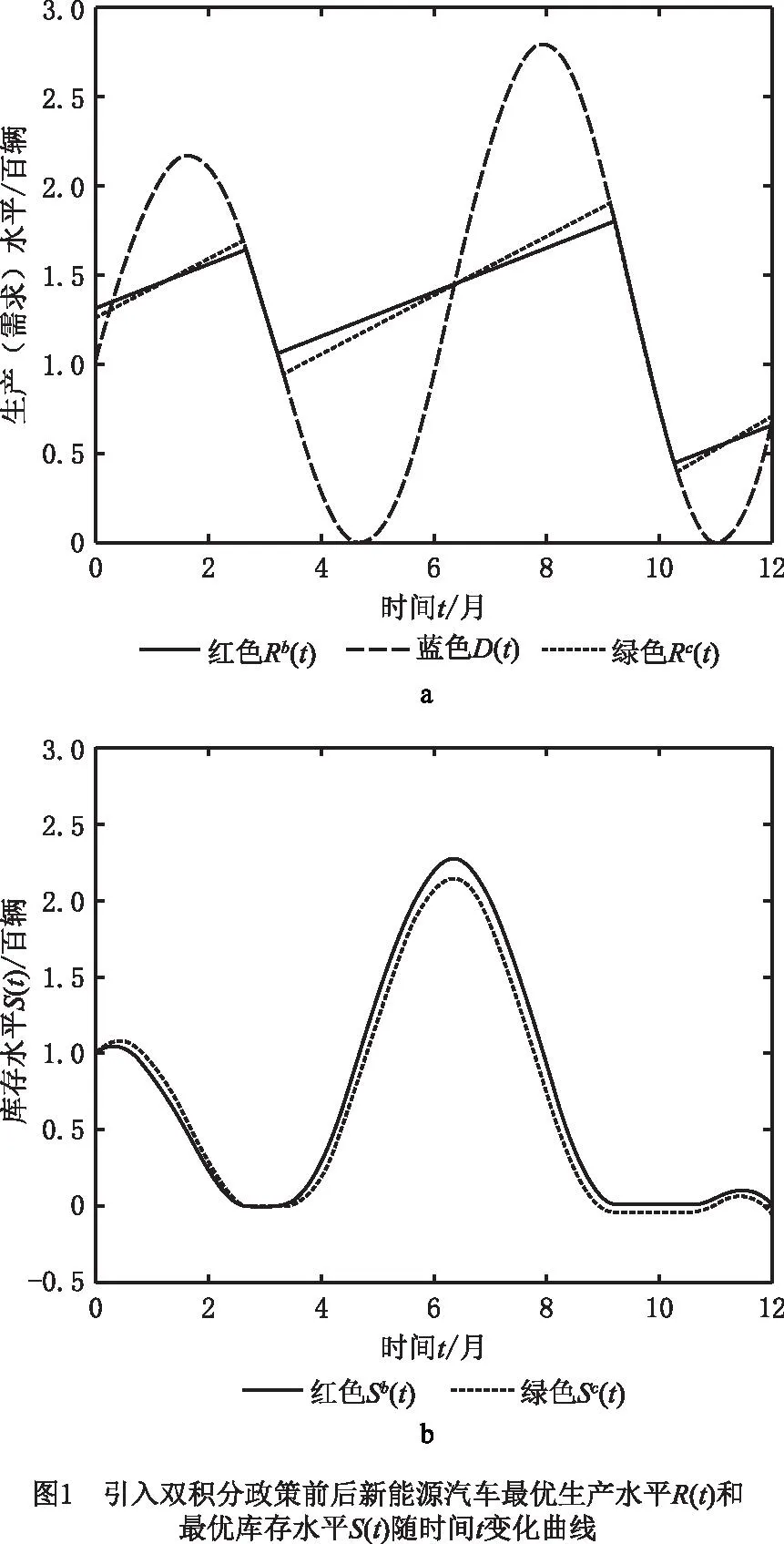
通过数值分析得出模型(Ⅰ)的最优解为{Rb(t),Sb(t)},图2a中Rb(t)表示双积分政策下新能源汽车的最优生产水平,图2b中红色线Sb(t)表示双积分政策下新能源汽车的最优库存水平。此时新能源汽车的最优成本为V=163.152(万元),最佳生产库存成本为V=173.982(万元),生产新能源汽车所产生的污染为αb=62.104(吨)。这意味着新能源汽车总成本降低了5.648%,生产库存成本增加了0.615%。

在模型(Ⅱ)中,假设单位体积温室气体的成本价格M(t)=50元,单位时间国家分配给该企业的碳排放额N=0.5(吨),新能源汽车数量与碳交易排放量比值θ=0.2,保持其他参数不变。那么模型如下:

s.t.

(41)

通过数值分析得出模型(Ⅱ)的最优解为{Rc(t),Sc(t)},图2a中Rc(t)表示碳交易和双积分政策下新能源汽车最优生产水平,图2b中Sc(t)表示碳交易和双积分政策下新能源汽车最优库存水平。此时新能源汽车的最优成本为V=157.813(万元),最佳生产库存成本为176.385(万元),生产新能源汽车所产生的污染为αc=65.731(t)。相比较双积分政策,新能源汽车总成本降低了3.272%,而新能源汽车生产库存成本增加了1.409%。

图1a和图2a分别为引入双积分政策前后和引入碳交易与双积分政策前后,新能源汽车最优生产水平随时间变化曲线图,从两图可以看出,考虑碳交易和双积分政策下,会使生产水平曲线变得更平滑,生产力更为均衡稳定,避免生产计划生产较大波动,同时也使得生产水平增加。图1b和图2b分别为引入双积分政策前后和引入碳交易与双积分政策前后,新能源汽车最优库存水平随时间变化曲线图,从两图中可以看出,考虑到碳交易和双积分政策下会使库存水平有明显增加,从而也在一定程度上刺激新能源汽车企业生产,以保证新能源积分的增加,以满足积分交易。

为了考察动态多周期对新能源汽车企业在生产量和库存水平的影响,采用与静态模型对比进行分析。其中静态模型的需求是一般函数,不像动态模型的需求函数是基于泛函,这意味着动态模型每个周期最优决策都随需求波动而实时改变,而静态模型则不会改变,但其生产产量和和生产成本受到上个周期库存状态影响而变化。基于此,分析对最优产量的影响,分别对应三个策略:没有考虑双积分和碳交易策略的基本模型、只考虑双积分策略的模型(Ⅰ)和同时考虑双积分和碳交易策略的模型(Ⅱ),如图3所示。

图3反映的是新能源汽车最优生产水平随时间变化曲线图,从图中可以看出,静态三个模型(虚线)比动态模型(实线)的波动小,反映模型只能单独短周期决策,难以进行预见性决策,实用性有限。由于动态的多周期前一个周期的产量和库存水平会影响到下个周期的生产,相反静态每个周期的决策生产量都是独立存在,也就是说动态多周期更能体现出生产实际情况。从具体策略来看,在静态模型中,同时考虑双积分和碳交易策略的模型(Ⅱ)的产量最大,只考虑双积分策略的模型(I)的产量次之,没有考虑双积分和碳交易策略的基本模型的产量最小。在动态多周期模型中,情况则较为复杂,在第1和第1.5个周期中,同时考虑双积分和碳交易策略的模型(Ⅱ)的产量最大,没有考虑双积分和碳交易策略的基本模型的产量最小;相反,在第1.5和第4.5个周期中,没有考虑双积分和碳交易策略的基本模型的产量最大,而同时考虑双积分和碳交易策略的模型(Ⅱ)的产量最小;在后期中,我们也发现同时考虑双积分和碳交易策略的模型(Ⅱ)的产量一直保持最大,并且随着时间推移,同时考虑双积分和碳交易策略的模型(Ⅱ)的产量的波动逐步减少;而没有考虑双积分和碳交易策略的基本模型的产量几乎一直最小。因此,也说明了在各个策略模型中,对于没有考虑双积分和碳交易策略,其动态和静态的产量差异最大;同时考虑双积分和碳交易策略,其动态和静态的产量差异次之;只考虑双积分策略其动态和静态的产量差异最小。

如图4所示为新能源汽车最优库存水平随时间变化曲线图。可知,图4与图3新能源汽车最优生产水平表现出相同的波动模式。不同的是,随着时间的推移,最优库存水平不断下降,而最优产量水平则呈现出波动上升的趋势。具体来说,静态三个模型(虚线)比动态模型(实线)的波动小,且在最后周期阶段(第8～第12周期),静态情况下,没有考虑双积分和碳交易策略的基本模型的库存水平最低,而其他考虑了双积分或碳交易策略的模型,则库存水平较高,说明了政策效果是鼓励新能汽车企业多生产新能源汽车来遏制传统燃油汽车的生产。通过图4发现,在经历开始2.5个周期后,不管是静态还是动态情况下,同时考虑双积分和碳交易策略的模型(Ⅱ)的库存水平都相对较高,而且波动最小,说明同时考虑双积分和碳交易策略的模型(Ⅱ)的达到一种稳态均衡,是一种较为理想状态。而对于没有考虑双积分和碳交易策略的基本模型以及只考虑双积分策略的模型(Ⅰ)的动态和静态的水平差异较大。其原因是动态比静态更能反映生产和库存的连续性,双积分策略和碳交易政策是两种相互制衡的策略,因此出现了上述动态的模型(Ⅱ)比基本模型和模型(Ⅰ)库存更容易管理和控制。

另外,为了考察新能源积分价格P(t)和单位体积碳交易的成本价格M(t)对新能源汽车总成本的影响。本文进行相应敏感度分析,如表2所示,可以看出新能源积分价格越高,将导致新能源汽车生产总成本越小,单位体积碳交易成本价格越高,也使得新能源汽车总成本越小。该图说明了通过市场机制,如果新能源积分交易价格和碳交易价格维持在一个较适中的水平,能很好促进新能源汽车企业的生产和应用推广,以及可持续发展。

表2 新能源积分价格P(t)和单位体积温室气体的成本价格M(t)对新能源汽车总成本的影响

4 结束语

本文利用动态最优控制理论研究在双积分和碳交易背景下新能源汽车企业生产和库存水平的最优解,探讨了双积分和碳交易政策对新能源汽车企业生产和库存水平的影响。首先运用Arrow-Karlin模型,进而引出双积分政策下的生产决策模型以及同时考虑双积分和碳交易政策下的生产决策模型。在上述三个模型下,以庞特亚里金最大值为入手点,探讨双积分和碳交易政策对生产水平和库存水平的影响;得出在在不同政策组合下,最优控制生产量和最优库存水平。最后通过数值分析验证上述三个模型的准确性和有效性。研究表明:①加入双积分和碳交易会使生产水平曲线变得平滑,生产更为稳定均衡。②加入双积分和碳交易更激励新能源汽车生产企业的生产积极性,因为相比没有采用双积分政策,如采用该政策则新能源汽车总成本降低了5.648%;同理相比采用双积分政策,而采用双积分和碳交易政策,则新能源汽车总成本降低了3.272%。③加入双积分和碳交易保证两者交易价格维持在一个适合水平,就能够帮助企业达到降低生产总成本的目的,从而有效促进节能减排的目的。④通过和静态模型相比较,发现对于没有考虑双积分和碳交易策略,其动态和静态的产量差异最大;同时考虑双积分和碳交易策略,其动态和静态的产量差异次之;只考虑双积分策略时动态和静态的产量差异最小。⑤不管是静态还是动态的情况下,同时考虑双积分和碳交易策略的模型(Ⅱ)的库存水平都相对较高,而且波动最小,说明同时考虑双积分和碳交易策略的模型(Ⅱ)的达到一种稳态均衡,是一种较为理想的状态。而对于没有考虑双积分和碳交易策略的基本模型以及只考虑双积分策略的模型(Ⅰ)的动态和静态的水平差异较大。

文章也存在如下几点局限和未来进一步可能研究方向:①模型没有考虑竞争的环境下,存在另外一个新能源汽车制造企业或是一个传统燃油车制造企业与之竞争,这种情况下实施双积分和碳交易政策带来优化结果的变化;②模型没有考虑到供应链背景下,上游供应商和下游制造商和分销商如何协调分担碳交易成本,或进行分担创新费用来促进减排降碳和双积分政策的实施。