带转移时间的资源受限项目鲁棒调度优化

胡雪君,梁 盛,王建江,崔南方

(1.湖南大学 工商管理学院,湖南 长沙 410082; 2.国防科技大学 系统工程学院,湖南 长沙 410073;3.华中科技大学 管理学院,湖北 武汉 430074)

0 引言

全球经济活动中有30%是采用项目形式执行,涉及年产值约27万亿美元。在项目管理过程中不可避免地会涉及到资源的使用,包括可更新资源(如劳动力、设备)和不可更新资源(如物料、资金)。资源受限项目调度问题(Resource-Constrained Project Scheduling Problem,RCPSP)研究的是在满足活动优先关系和资源约束(主要指可更新资源)的前提下,制定出满足项目预期目标(比如完工时间最短)的基准调度计划(baseline schedule),作为资源分配、活动开工的基础以及项目各利益方协调的依据,科学有效的项目调度计划与资源配置方案有助于提高企业项目管理的效率[1-2]。现实中,如果资源在项目间或活动间的时移时间与活动工期相比无法忽略,就有必要在制定项目调度计划时考虑资源的转移时间,例如建筑工程项目中重型机械设备(起重机等)从一个位置移动到另一个位置需要移动和调试时间。此外,资源必须根据活动内容进行调整时也需要相应的准备时间,例如机器生产不同的产品时须进行清洗、IT项目中人力资源往往需要时间熟悉新工作等[3-4]。这类问题称为带转移时间的资源受限项目调度问题(RCPSP with Transfer Times,RCPSP-TT)。

目前,针对RCPSP-TT问题,只有少数学者进行了研究。KRÜGER等[4]根据可更新资源是否可以自主转移,将转移资源划分为不同的类型,并考虑资源转移成本建立了混合整数规划模型;KRÜGER等[5]分别以最小化项目总工期和项目平均工期为目标建立RCPSP-TT优化模型,提出了基于活动列表的串行调度和并行调度启发式算法;POPPENBORG等[6]针对RCPSP-TT问题设计了一种基于资源流的禁忌搜索算法,该算法利用资源流表示问题的解,并基于串行调度和并行调度机制提出了资源流邻域算子;胡雪君等[7]在文献[6]研究工作的基础上,以找到时间最短的关键路径为基准,合理改进了邻域算子的选择方式,进一步设计了改进的禁忌搜索算法和贪心随机自适应搜索算法,模拟实验表明两种算法均可针对更多的项目实例求得最优解;KADRI等[8]结合调度生成机制和优先级规则提出一种遗传算法求解RCPSP-TT问题,采用活动列表编码对调度方案进行描述,设计了基于双点交叉和概率变异的遗传操作;文献[9-10]提出一种内嵌分支定界寻优搜索的遗传算法,设计了一种适应算法结构的基于活动绝对顺序的编码策略;文献[11]针对带资源转移时间的多技能RCPSP问题开展研究,考虑资源技能的不确定性建立了一个鲁棒优化模型,提出了一种新的遗传算法求解模型。此外,文献[12-15]针对多项目环境下带资源转移时间的项目调度问题开展了研究。

然而,上述研究绝大多数都是在确定条件下开展的,大都以项目完工期最短为优化目标,不能适应复杂环境中不确定性对项目的规划和调度提出的高要求。鲁棒性项目调度作为解决不确定条件下项目调度问题的有效方法,近些年来受到了学者们的广泛关注[16-17]。该方法在充分挖掘和利用不确定信息的基础上,主动采取一些必要措施,生成“受到保护的”、抗干扰能力强的前摄调度计划,使不确定性因素对方案执行的影响最小化。学术界将项目调度的鲁棒性分为质鲁棒性和解鲁棒性两种:质鲁棒性(quality robustness)是指基准计划对应的目标函数值(如项目工期、成本等)对干扰因素的不敏感性;解鲁棒性(solution robustness)是指基准计划与项目实际执行时进度计划之间的差别大小[18-19]。

为提升项目调度方案的解鲁棒性,文献中广泛探讨了两种主要方法,即时间缓冲(time buffering)和鲁棒资源分配(robust resource allocation)。前者是指在项目活动前加入缓冲时间用以吸收各种不确定因素的干扰,阻止其在调度计划中的传播,保证项目尽可能按基准计划进行[20];后者旨在通过优化项目活动间可更新资源传递的路径(资源流网络)来提升调度计划的稳健性[2,21]。针对鲁棒资源分配问题,LEUS等[21]提出保护基准计划不受活动工期变动干扰的资源流网络优化模型,采用分支定界算法求解单资源小规模问题,其目标函数是最小化活动实际开始时刻偏离计划开始时刻的惩罚成本;DEBLAERE等[22]考虑活动工期的不确定性,为了提升项目调度计划的鲁棒性,分别提出了三种混合整数规划模型和一种MABO(myopic activity-based optimization)启发式算法,该算法通过仿真模拟和局部寻优的方式构建稳定的资源流网络。考虑到模拟方法不能保证资源分配方案的唯一性,文献[2]和文献[23]对MABO算法进行了改进,采用一种拖期惩罚成本指标来评估可行资源分配方案的鲁棒性,仿真实验证明该方法获得的资源流网络具有唯一性,并且大大降低了算法计算量;文献[24]提出一种基于前向活动优先级的鲁棒资源分配启发式算法,实验证明该方法可以减少资源传输形成的额外工序约束,提升调度计划的鲁棒性。此外,胡雪君等[26]、WANG等[27]考虑资源转移成本建立鲁棒资源分配优化模型,不同于以往研究均采用基于活动的资源流描述,他们定义了基于资源的二元决策变量来表示资源在活动间的传输次序。需要指出的是,上述研究都是基于活动开始时间已知的调度计划对资源流进行决策(两阶段),忽略了活动安排和资源转移决策的相互影响及协调。

资源流网络优化为研究不确定项目调度问题提供了一种新的思路。但是,现有鲁棒资源分配相关文献都是针对传统RCPSP开展研究,忽略了资源转移时间对活动进度计划和资源分配方案鲁棒性的影响,难以适用于带转移时间的RCPSP-TT问题。针对已有研究的局限性,本文同时考虑资源转移时间和活动工期的不确定性,将问题建模为集成的鲁棒项目调度问题,即针对活动调度和资源转移同时进行决策。本文的主要研究贡献体现在以下三个方面:①针对RCPSP-TT问题特征,分别从资源转移关系、活动时差、随机活动工期3个不同角度设计了三种解鲁棒性代理指标,构建了两个混合整数规划模型(minEA,maxPF)和一个随机规划模型(minTPC);②通过引入辅助变量将maxPF模型线性化为可采用CPLEX优化软件求得最优解,并设计了求解minTPC模型的改进禁忌搜索启发式算法;③设计大规模仿真实验对不同优化模型及算法的有效性进行对比分析,并给出了相应的管理启示。

1 问题描述

采用节点式网络G(N,A)表示一个项目,记活动集合为N={0,1,…,n,n+1},其中序号0和n+1分别代表虚拟首活动和虚拟尾活动,A代表活动之间的结束-开始型工序优先关系(i,j)的集合。记资源种类集合为K,第k(k=1,2,…,K)种资源的可用量为ak。由于资源的约束性,有限的资源在项目活动节点间传输会形成资源驱动的新工序约束,假设活动i完工后,其占用的资源部分或全部分配给了活动j,则活动i和j之间就存在一条资源流,fijk(i,j∈N,k∈K)表示从活动i流向活动j的资源k的数量。fijk>0表示活动i和j之间存在资源转移关系,以一条资源弧(i,j)k连接活动i和j;将所有的资源弧集合定义为AR,构成了项目资源流网络G(N,AR)。资源k从活动i流向活动j需要一定的资源转移时间Δijk≥0,且满足三角形规则,即Δihk+Δhjk≥Δijk,∀i,j,h∈N。

本文所研究的鲁棒RCPSP-TT具体表述为:项目决策者需要同时考虑工序优先关系、资源可用量约束、项目交付期限以及随机活动时间,确定如何安排活动执行顺序及资源转移次序,以使调度计划的解鲁棒性(稳定性)最强。问题相关参数及含义如表1所示。

图1描述了一个带资源转移时间的项目网络示例,其中实箭线表示活动之间的工序优先关系。该项目包括8个活动(其中0和7为虚拟活动),只用到一种可更新资源(下文省略下标k),资源总量为10。

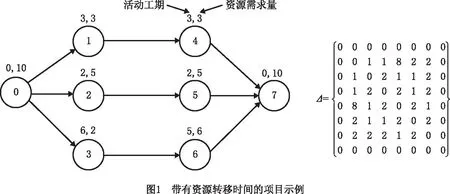
图2a和图3a分别给出了两个可行的资源转移方案,其中虚箭线表示资源驱动的新工序约束(额外资源弧),实箭线弧和虚箭线弧上数字均代表资源转移数量。采用文献[4]中的并行调度(Parallel Schedule Generation Scheme,PSGS)策略与最早开始时间(Earliest Starting Time,ES)优先规则对资源流网络G(N,A∪AR)进行解码,则可得到如图2b和图3b所示的项目调度计划,对应的项目工期均为14。

分析图2和图3可知,由于两个可行方案中资源转移关系及转移时间的不同,同等程度的工期扰动对两个方案的鲁棒性具有不同的影响。例如,第一种情况,假设活动5的实际工期拖延1个时间单位,对于方案I,将导致活动6的开始时间推迟一个单位,项目完工期保持14不变;而对于方案Ⅱ,同样导致活动6的开始时间推迟一个单位,并且导致项目延迟一个单位时间完工(即项目完工期为15)。第二种情况,假设活动1的实际工期拖延1个时间单位,对于方案Ⅰ,将导致活动4的开始时间延迟一个单位,最终导致项目延迟一个单位时间完工(即项目完工期为15);而对于方案Ⅱ,将导致活动4、活动5、活动6的开始时间都推迟一个单位,项目同样延迟一个单位时间完工。值得注意的是,第二种情况下虽然项目完工期都是延迟1个单位时间,但是对后续活动调度计划的影响不同,方案Ⅰ仅影响了后续一个活动(活动4),方案Ⅱ影响了后续三个活动(活动4,5,6),因此对项目调度计划的扰动差异导致不同调度方案的解鲁棒性不同。那么,如何判断上述哪一种调度方案应对活动拖期风险的能力更强?为此,需要设计合理的鲁棒性衡量指标,并在此基础上建立集成的RCPSP-TT前摄调度优化模型。

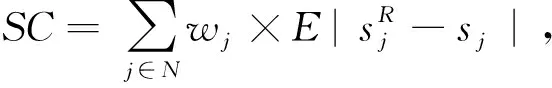
2 混合整数规划模型

本节分别以最小化资源弧数量和最大化活动成对时差为鲁棒性代理指标,构建RCPSP-TT前摄调度模型。模型决策变量定义为:

sj为活动j的计划开始时间(sj∈Z+),j∈N;

∀t=1,…,T,j∈N;

fijk为活动i流向活动j的第k种资源的数量,i,j∈N,k∈K;

2.1 最小化资源弧数量(MinEA)

DEBLAERE等[22]的研究表明,项目活动之间由于资源转移而施加的额外优先关系(资源弧)的数量越少,进度计划执行通常越稳定;但是他们的研究是基于活动开始时间已知的初始调度计划构建资源流网络,且没有考虑资源转移时间对项目调度方案的影响。为此,本节补充定义0-1决策变量zij,如果任一资源k∈K从活动i流向活动j,zij=1;否则,zij=0。以最小化额外资源弧(Extra Arcs,EA)数量为优化目标,针对RCPSP-TT建立MinEA模型如下:

(1)

s.t.

si+di-sj≤0,∀i∈J∪{0},j∈Succi;

(2)

si+di+Δijk-sj≤T(1-yijk),
∀i∈J∪{0},j∈Jri,k∈K;

(3)

(4)

(5)

(6)

fijk≤yijk×min{rik,rjk},
∀i∈N,j∈Jri,k∈K;

(7)

yijk≤fijk,∀i∈N,j∈Jri,k∈K;

(8)

(9)

sn+1≤D;

(10)

xjt={0,1},∀t=0,…,T,j∈N;

(11)

fijk∈Z+,yijk={0,1},
∀i∈J∪{0},j∈Jri,k∈K;

(12)

(13)

yijk≤zij,∀i∈J∪{0},j∈Jri,k∈K;

(14)

zij∈{0,1},∀i∈J∪{0},j∈Jri。

(15)

式(2)是活动优先关系约束,即活动i完成之前,其紧后活动j不能开始;式(3)表示活动开始时间与资源转移时间的关系,即如果资源k从活动i与转移到活动j,则活动j必须在活动i结束且资源转移完成之后才能开始;式(4)表示任意活动j只能在一个时间点开始;式(5)表示活动开始时间sj与决策变量xjt的关系;式(6)是资源流平衡约束,表示流入活动j的资源k的总量与流出该活动的资源k的总量须相等,且等于该活动对资源k的需求量;式(7)和式(8)共同定义了yijk和fijk之间的关系,即当活动之间存在资源转移时,yijk=1,否则yijk=0;式(9)是资源需求约束,表示任意时刻正在进行的活动对于资源k的消耗量不超过资源总供应量;式(10)为项目交付日期约束;式(11)～式(12),(15)定义了决策变量的可行域;式(13)表示对任意资源k∈K,从虚拟首活动流出的资源数量等于流入虚拟尾活动的资源数量,并且都等于该资源的可用量ak;式(14)表示对任意资源k∈K,只要yijk取值为1(即fijk>0),则zij=1。

2.2 最大化成对时差(MaxPF)

基于时差的鲁棒性代理指标具有不需要考虑不确定事件的相关信息、不依赖于模型仿真等优势,是一种衡量解鲁棒性的主要方法[20]。一般而言,如果活动i和j之间的自由时差越大,其吸收工期扰动的能力越强,即前序活动i拖期对后序活动j的影响越小。因此,部分学者考虑增加具有前后序关系的两两配对活动之间的时差,以达到提高调度方案鲁棒性的目的[28]。针对RCPSP问题,DEBLAERE等[22]对于所有满足si+di≤sj的活动对(i,j),定义了一个成对时差(pairwise float)指标,其值等于活动j的开始时间与活动i的结束时间之差,PFij=sj-(si+di)。需要注意的是,文献[22]关于时差的定义不适用于本文研究的RCPSP-TT问题。首先,文献[22]是在活动开始时间sj(j∈J)已知的基础上定义活动时差,即所有活动前后序关系已知,因此活动对(i,j)的时差PFij可以作为参数,在问题建模前计算获得。

例如,针对图3所示的资源流网络与项目调度方案Ⅱ,从活动2到活动6存在两条资源转移路径。路径2-4-6的成对时差之和为PF2,4,1+PF4,6,1=0+2=2;另一条路径2-5-6的成对时差之和为PF2,5,1+PF5,6,1=2+0=2。因此,MSPF2,6,1=min{2,2}=2,由于该案例仅包含一种资源,所以pf26=MSPF2,6,1=2。这意味着活动2可以拖期2个单位完工而不影响活动6的开始。显然,pfij值越大,对应的项目调度计划及其资源流网络越稳定。

基于以上定义,以最大化活动成对时差总和为目标,建立MaxPF模型如下。

(16)

s.t.约束(2)～约束(12);

PFijk=max{0,sj-(si+di+yijkΔijk)},
i∈J∪{0},j∈Jri,k∈K;

(17)

MSPFijk≤PFilk+MSPFljk,i∈J∪{0},
j∈Jri,l∈Succi∩Jsj,k∈K;

(18)

MSPFijk≤PFilk+MSPFljk+M(1-yilk),
i∈J∪{0},j∈Jri,l∈Jri∩Jsj,k∈K;

(19)

MSPFijk≤PFijk,i∈J∪{0},j∈Succi,k∈K;

(20)

MSPFijk≤PFijk+M(1-yijk),
i∈J∪{0},j∈Jri,k∈K;

(21)

MSPFiik=0,i∈J∪{0},k∈K;

(22)

MSPFijk≤C,i∈J∪{0},j∈Jri,k∈K;

(23)

pfij≤MSPFijk,k∈K;

(24)

MSPFijk∈Z+,i∈J∪{0},
j∈Jri,k∈K。

(25)

式(16)为目标函数,表示最大化所有可能发生资源转移的活动对(i,j)的成对时差之和。式(17)表示对任意资源k∈K,如果活动j在活动i完成之后开始,则时差PFijk=sj-(si+di+yijkΔijk),否则PFijk=0;式(18)～式(19)以递归的方式计算(i,j)k的成对时差,式(18)对于(i,j)k定义了三角不等式,其中活动l是活动i的直接紧后工序,式(19)中如果可能的资源弧(i,l)k不存在(yilk=0),则式(19)不具有约束力,其中M是一个充分大的常数(下同);式(20)针对活动j是活动i的直接紧后工序的情况,给出了(i,j)k成对时差的上限;类似地,式(21)中如果可能的资源路径(i,j)k不存在,则式(21)不具有约束力;式(22)表示每个活动相对于其自身的成对时差为0。需要指出的是,对于(i,j)k,如果所有的MSPFijk相关约束都不具有约束力,则说明活动i和j是工序优先关系独立且资源关系独立的一对活动,此时MSPFijk将达到一个最大值C,如式(23)所示;式(24)表示成对时差pfij值等于所有资源种类k∈K中MSPFijk的最小值;式(25)为变量MSPFijk的可行域。需要注意的是,任意(i,j)k之间只要存在可能的资源路径即可计算成对时差PFijk和MSPFijk,不需要存在直接的资源弧。

显然,由于约束(17)是非线性约束,上述模型不能直接求解。因此,需要将约束(17)重新表述为:

PFijk≥max{0,sj-(si+di+yijkΔijk)},
i∈J∪{0},j∈Jri,k∈K;

(26)

PFijk≤max{0,sj-(si+di+yijkΔijk)},
i∈J∪{0},j∈Jri,k∈K。

(27)

对于式(26),很容易将其线性化如下:

PFijk≥0,i∈J∪{0},j∈Jri,k∈K;

(28)

PFijk≥sj-(si+di+yijkΔijk),
i∈J∪{0},j∈Jri,k∈K。

(29)

但是,对于式(27),则需要引入辅助变量φijk,i∈J∪{s},j∈Jri,k∈K。如果sj-(si+di+yijkΔijk)≥0,φijk=1;否则,φijk=0。因此,可以将式(27)重新表述如下:

PFijk≤sj-(si+di+yijkΔijk)+M(1-φijk),
i∈J∪{0},j∈Jri,k∈K;

(30)

PFijk≤Mφijk,i∈J∪{0},
j∈Jri,k∈K;

(31)

sj-(si+di+yijkΔijk)+M(1-φijk)≥0,
i∈J∪{0},j∈Jri,k∈K;

(32)

sj-(si+di+yijkΔijk)-Mφijk<0,
i∈J∪{0},j∈Jri,k∈K。

(33)

式(30)表示如果活动j在活动i完成之后开始,则PFijk=sj-(si+di+yijkΔijk);否则,PFijk=0,如式(31)所示。式(32)～式(33)表示如果sj-(si+di+yijkΔijk)≥0,则φijk=1;如果sj-(si+di+yijkΔijk)<0,则φijk=0。

3 随机规划模型与禁忌搜索算法

3.1 随机规划模型MinTPC

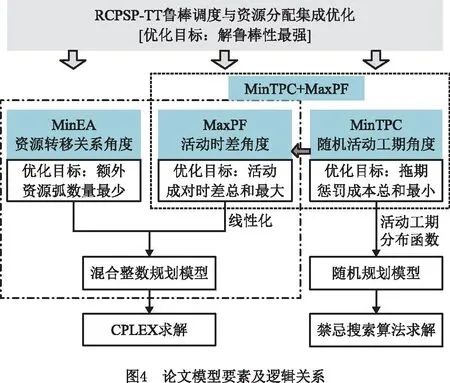
上述MinEA和MaxPF模型分别采用基于资源流和基于时差的鲁棒性代理指标构建优化模型,其优化目标和约束条件中均不包含随机变量,并没有显性考虑活动工期的不确定性。本节综合考虑随机活动工期、资源转移关系和转移时间、活动开始时间偏离成本等项目特征,针对RCPSP-TT提出一种总拖期惩罚成本(Tardiness Penalty Cost,TPC)指标,从概率论的角度衡量项目计划解鲁棒性。活动j的tpcj定义为活动延迟开工造成的期望损失,表示为[25-27]:

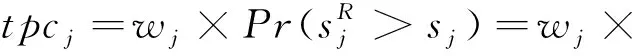
(34)

据此,以最小化项目总拖期惩罚成本为优化目标,建立MinTPC模型如下:

(35)

满足约束(2)～约束(12)。

3.2 禁忌搜索算法

上述MinTPC模型中含有随机变量,目标函数非凸且不具有明确的表达式,不能采用规划软件或者精确算法直接求解。元启发式算法(或称智能算法,metaheuristics)为求解优化问题提供了通用的算法框架,其通常能在可接受的时间内求得大规模问题的满意解(甚至最优解),能够较好地满足实际应用需求。其中,禁忌搜索(Tabu Search,TS)智能优化算法是一种全局性邻域搜索算法,该算法不论在RCPSP还是鲁棒项目调度中都得到了广泛应用,在该领域呈现了较强的适用性和优秀的性能[3,29-31]。因此本文在POPPENBORG等[6]、胡雪君等[7]研究工作的基础上,设计了改进的禁忌搜索算法对模型求解。

3.2.1 编码与解码设计

针对RCPSP-TT问题,文献[6-7]以资源流量fijk(i,j∈N,k∈K)作为解向量进行编码(记为资源流列表ResF),并从理论上证明了资源流编码方式一定能够得到最短工期问题的最优解。本文MinTPC模型旨在给定完工期限约束下最小化项目总拖期惩罚成本,因此为了进一步增加调度方案的鲁棒性,采用在项目活动前插入时间缓冲的方法来吸收工期扰动,即在资源流列表ResF基础上,定义一组时间缓冲列表Buf=(B0,B1,…Bn,Bn+1),其中元素Bj∈Z+表示活动j∈N之前插入的缓冲大小,Bj=0表示活动j之前没有缓冲。采用“资源流-缓冲”列表的混合编码表示可行解的结构,记为Ind={ResF,Buf}。

对以上编码进行解码时,按照改进的并行调度策略与ES优先规则进行,获得工序和资源可行的项目调度计划。解码之后需要判断解方案是否可行,判断准则为项目是否在截止期D之前完工:如果是,则为可行解;否则为非法解。

3.2.2 邻域操作

本文TS算法分别针对资源流列表ResF和缓冲列表Buf进行邻域操作,以获得当前解的邻域解。其中,当前缓冲列表的邻域解由每个活动前的缓冲大小增加或者减小一个单位产生;当前资源流列表的邻域解由重构算子Nreroute和反转算子Nreverse生成。其中,反转邻域算子详见文献[6-7],此处不再赘述。

重构领域算子操作如下所述。选择两条资源弧(i,j)k和(u,v)k,其中资源弧(i,j)k从关键路径中选择,(u,v)k任意选择,满足如下条件:①资源转移量fijk>0,fuvk>0;②在集成资源流的网络(N,A∪AR)中,活动j与活动u之间、活动v与活动i之间均不存在紧前关系。然后,按照以下方式对资源流网络进行重构:f′ijk=fijk-q,f′uvk=fuvk-q,f′ivk=fivk+q,f′ujk=fujk+q,取q=min{fijk,fuvk}。基于图1所示的RCPSP-TT项目案例,图5给出了对一个可行资源流网络进行重构操作的示例,其中点状虚线表示关键路径,选定的两条资源弧分别为(1,4)和(2,5)。

类似地,采用改进的PSGS策略与ES优先规则对插入缓冲的网络G(N,A∪AR)进行解码,如果得到的项目完工期在截止期限以内,该邻域解为候选解;否则,该邻域解不成立。此外,当流入某活动的可用资源总量超过该活动所需资源数量时,还须定义相应的资源转移优先规则,本文采用minGAP规则,即选择资源最早到达时间与活动开始时间之差最小的活动进行资源转移。

3.2.3 TS算法流程

基于以上编码、解码和邻域操作,本文设计了带精英解策略的禁忌搜索算法对MinTPC模型求解,算法流程如图6所示。

本文实验中,TS算法终止条件设定为最大迭代次数Iter=10 000。每次迭代中,最多访问50个重构邻域解Nreroute,以及5个反转邻域解Nreverse。算法搜索过程中最多保留1个精英解,当最优解未改进代数达到阈值p=750或不存在可行邻域解时,则搜索过程从当前精英解重启;如果当前最优解未改进代数达到阈值q=1 500时,则采用并行调度算法重新生成初始解,重启搜索过程。禁忌表的长度设为Ttabu=rand(a)+a·|N|,其中|N|为邻域解数量,a=5,a=0.3[7]。

3.3 MinTPC与MaxPF混合优化模型

上述MinEA和MaxPF模型均为混合整数线性规划模型,可以采用CPLEX优化软件进行求解,但是求解时间随着问题规模呈线性增长。通过预实验结果可知,由于MaxPF模型结构复杂,变量数多,难以在有限的时间和空间内求解得到模型最优解(活动数量为30),针对部分复杂问题实例甚至难以直接求解得到可行解。因此,本节提出MinTPC与MaxPF混合优化策略,对MaxPF模型进行降维:首先,通过求解MinTPC获得一个初始资源流网络和初始调度计划;然后,将初始调度计划中的活动开始时间作为已知参数,代入MaxPF模型,以最大化活动成对时差总和为优化目标(公式(16)),进一步优化资源流决策,进而生成抗干扰能力强的前摄调度集成优化方案,该方法记为MinTPC+MaxPF。

3.4 具体算例

本节以图1所示的带资源转移时间的项目网络为例,分别采用MinTPC、MinTPC+MaxPF、MinEA、MaxPF方法获得活动开始时间与资源分配方案(取σ1=0.5),调度结果如图7所示。

其中,图7a和图7b是采用MinTPC和MinTPC+MaxPF方法生成的解方案,二者对应的项目调度计划具有相同的活动开始时间,但是资源转移方式不相同。例如,图7a中活动5所需资源由活动1和活动3提供,活动3的完工时间是6,活动5的开始时间是7,资源从活动3流向活动5需要的转移时间为△35=1,因此活动3、活动5之间没有时间缓冲,活动3一旦拖期一定会影响活动5的正常开工;而采用MinTPC+MaxPF方法基于相同的活动进度计划进一步优化资源转移决策(如图7b),活动5所需资源由活动1和活动2提供,活动2的完工时间是2,资源从活动2流向活动5需要的转移时间为△25=1,因此活动2、活动5之间有4个单位的时间缓冲,活动2至少发生4个时间单位的拖期才会影响到活动5按计划开工。可见,针对本例图7a和图7b两种资源分配方案,采用MinTPC+MaxPF方法可以更有效应对活动的拖期风险,提升调度计划的鲁棒性。

图7c和图7d是采用MinEA和MaxPF方法生成的解方案,二者对应的资源流网络完全相同(只有一条额外资源弧(5,6)),但是活动开始时间不一样。图7c中活动5的开始时间是4,图7d中活动5的开始时间是3;这意味着图7d中活动2一旦拖期一定会导致活动5不能按照基准计划开工(△25=1),而图7c中活动2、活动5之间有一个单位的时间缓冲,活动2延迟一个时间单位完工不影响活动5正常开始。可见,针对本例图7c和图7d两个调度方案,MinEA方法比MaxPF方法应对活动拖期风险的能力更强。

以上分析进一步表明,现有鲁棒资源分配相关研究基于活动开始时间已知的项目调度计划去优化资源分配决策,实际上具有一定的局限性,不能保证从全局角度获得鲁棒性最优的解方案,因而有必要对活动进度安排和资源转移决策进行集成优化。

4 模拟实验

为进一步评价上述4种优化方法得到的项目调度计划和资源分配方案的鲁棒性优劣,本章设计了一系列仿真实验,模拟工期不确定环境下的项目实际运行情况。所选取的测试集为KRÜGER等[4]基于PSPLIB标准例库[32]构建的RCPSP-TT标准问题集[6,8],其中由30个活动组成的J30例库包含480个项目实例,每10个为一组,每组具有相同的网络参数和资源参数。

MinTPC模型及禁忌搜索算法采用MATLAB编译程序;MinEA和MaxPF模型采用CPLEX优化软件求解,软件求解时间限制为5分钟。程序运行在CPU为Intel(R)Core(TM)i7-1165G7@2.80 GHz、内存为16G的个人电脑,操作系统为Windows 10。

4.1 实验设置

仿真实验相关参数的设置如表2所示。需要注意的是,由式(34)可知,总拖期惩罚成本TPC值与工期不确定水平有关,不同的不确定水平下MinTPC方法获得的解方案可能不相同。本文假设活动工期服从均值为基准计划时间dj、标准差为σ的对数正态分布[23,26-27],以σ1来衡量计划阶段预估的工期波动水平,以σ2来衡量模拟执行阶段的实际不确定水平。考虑到项目管理者在制定计划时通常很难准确预知项目在执行阶段的实际不确定水平,本文将计划阶段的工期不确定水平分别设置为低(L)、中(M)、高(H)3个等级(σ1={0.3,0.5,0.8}),不同等级对应的优化模型分别记为MinTPCL、MinTPCM、MinTPCH。

表2 仿真实验参数设置

模拟实验定义了以下两种鲁棒性绩效评价指标:

4.2 实验结果及分析

对以上6种RCPSP-TT前摄调度方法所得解方案进行仿真实验,表3和表4分别给出了项目交付日期D=1.1Cmax时的实验结果。两表中加粗数字表示分别按照3种不确定水平(σ1∈{L,M,H})制定前摄调度计划时,三种MinTPC方法中鲁棒性绩效最优的一种;加粗数字表示6种方法中鲁棒绩效最优的一种(下同)。

表3 D=1.1Cmax时不同方法的SC值对比结果

表4 D=1.1Cmax时不同方法的PCT值对比结果

通过对表3和表4统计数据的分析,可以得到以下结论:

(1)随着项目执行时不确定水平σ2的增大,每种方法的进度不稳定惩罚成本SC均增大,模拟完工期PCT均变长,这一结果与预期相符。显然,活动时间波动性越大,项目执行时偏离原定计划的可能性越大,导致惩罚成本增加;另外,随不确定性增大前序活动工期延迟带来的累积效应越强,最终导致项目完工期变长。

(2)在3种计划不确定水平下,分析MinTPCL、MinTPCM和MinTPCH所得结果可知:如果项目决策者更加追求解鲁棒性(即最小化惩罚成本),则按照低不确定水平(σ1=0.3)制订计划可以获得更加稳定的调度方案;如果追求更短的项目完工期,建议按照高不确定水平(σ1=0.8)制订计划。此外,三种MinTPC方法的SC值、PCT值之间的差距并不显著,说明即使项目管理者不能准确预知工期不确定水平,采用MinTPC方法也能够有效规避随机活动工期对优化模型的影响,从而指导管理者制订具备参考价值的前摄调度计划。

(3)相同σ2水平下,SC指标的优劣顺序为MinTPC+MaxPF≻MinEA≻MinTPC≻MaxPF,PCT指标的优劣顺序为MinTPC+MaxPF≻MinTPC≻MinEA≻MaxPF,其中“≻”表示“优于”。

一方面,在3种不确定水平下,采用MinTPC+MaxPF方法都能得到最短的项目完工期和最低的惩罚成本,而MaxPF方法所得基准方案的模拟完工期最长、惩罚成本最高。如前所述,采用CPLEX工具求解MaxPF模型所需时间较长,实验中将单个算例求解时间限定在5分钟以内,对于部分项目算例该方法在规定时间内不能求得最优解,只能得到近优解。为解决这一问题,本文提出了MinTPC+MaxPF混合优化方法,首先以最小化总拖期惩罚成本为目标生成初始活动调度和资源转移方案,其次以初始调度计划中的活动开始时间为已知变量,以最大化活动间成对时差总和为目标进一步优化资源流决策,仿真结果表明该方法所得项目调度方案的解鲁棒性和质鲁棒性绩效都是最好的。

另一方面,对于MinEA和MinTPC方法,解鲁棒性和质鲁棒性呈现相互冲突的关系:MinEA方法获得的基准方案最稳定,惩罚成本SC最小,说明以最小化额外资源弧数量为解鲁棒性替代指标要优于采用总拖期惩罚成本指标。

进一步地,模拟实验测试了项目交付日期分别取为D=1.2Cmax时D=1.3Cmax时各个模型和算法的鲁棒性绩效,结果分别列于表5和表6。为了直观显示三种交付期限下项目鲁棒性绩效指标的变化趋势,图8综合展示了表3～表6中σ2=0.5情况下的数据(另外两种不确定水平下的变化趋势与此相似)。

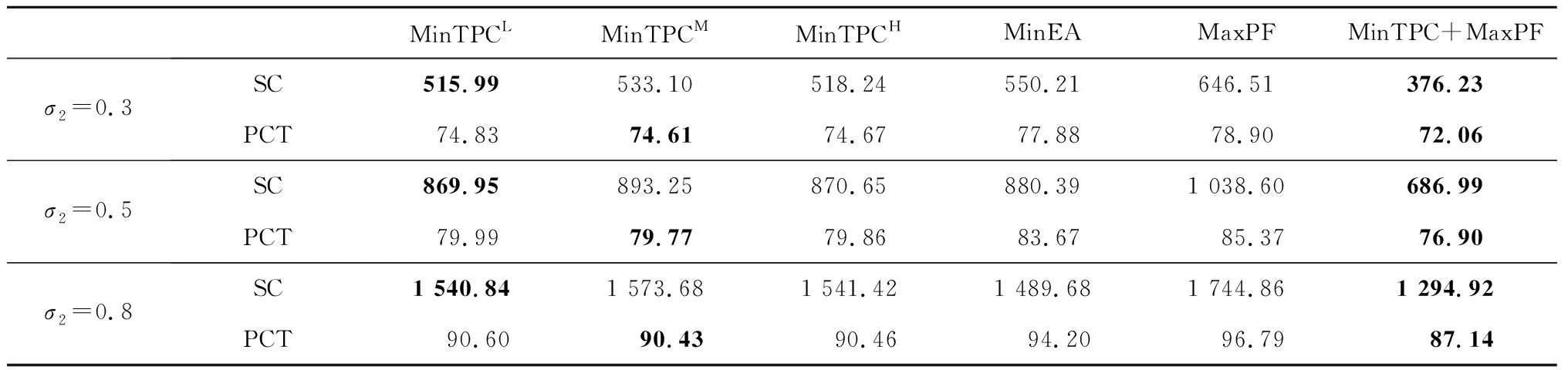
表5 D=1.2Cmax时不同方法的鲁棒绩效对比结果

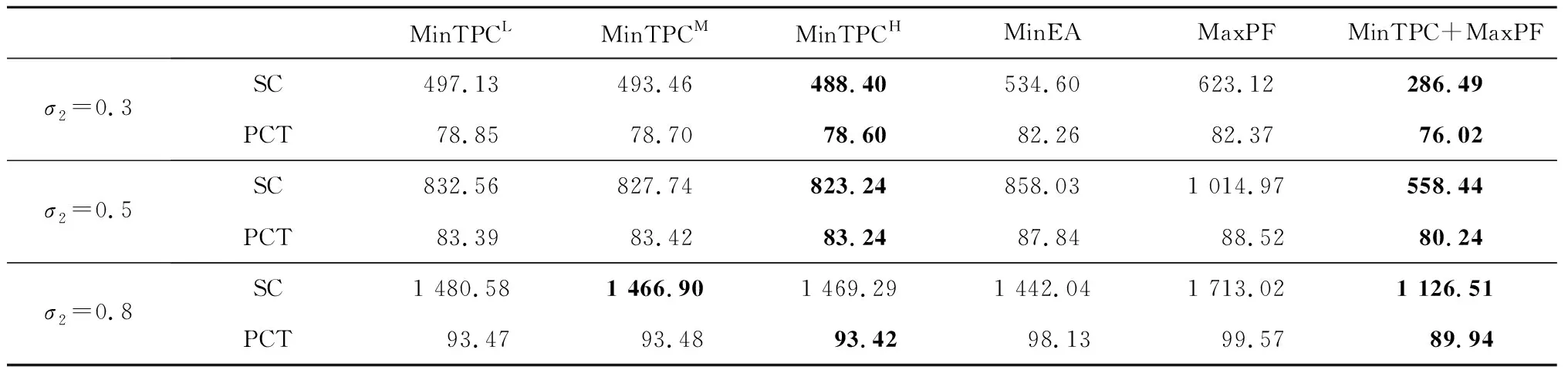
表6 D=1.3Cmax时不同方法的鲁棒绩效对比结果

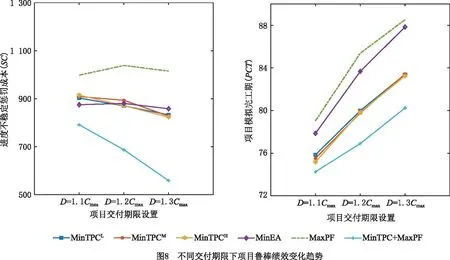
分析表5和表6可知,上述第(1)和第(3)条结论仍然成立,MinTPC+MaxPF方法相比其它方法产生的进度偏差最小且模拟完工期最短;与D=1.1Cmax结果不同之处在于,当项目完工期限最为宽松(D=1.3Cmax)时,运用MinTPC方法时按照高不确定水平(σ1=0.8)做计划,生成的活动调度和资源转移方案其解鲁棒性和质鲁棒性整体最优。此外,从图8可以看出,随着项目交付期限的延长,MinTPC和MinTPC+MaxPF方法的惩罚成本SC呈下降趋势,即项目稳定性增强,其中MinTPC+MaxPF集成优化方法的降幅最大;MaxPF方法的稳定性呈现先下降后增强的变化趋势;MinEA方法的SC值随项目交付日期延长变化不大,因为MinEA模型的优化目标是最小化额外资源弧的数量,与活动开始时间早晚没有直接关系。

我们知道,RCPSP-TT是RCPSP的拓展问题,因此,为了显示所提优化模型应用于基础RCPSP问题的普适性与差异性,另以PSPLIB_J30标准例库(资源转移时间均为0)为测试集进行仿真实验。表7列出了项目交付日期D=1.2Cmax的实验结果,由于项目交付日期D=1.1Cmax和D=1.3Cmax所得结论相类似,此处不再赘述。

表7 不同方法应用于基础RCPSP的鲁棒绩效对比结果(D=1.2Cmax)

从表7可以看出,针对不考虑资源转移时间的RCPSP问题,MinTPC+MaxPF方法在3种仿真不确定水平下仍然都能获得最低的惩罚成本和最短的项目模拟完工期,说明本文针对RCPSP-TT提出的MinTPC+MaxPF混合优化方法同样适用于求解RCPSP问题,并且能在很大程度上保证获得鲁棒性能最优的活动调度计划与资源分配方案。此外,对于MinTPC方法,当决策者在计划阶段不能明确预知项目实际执行时的工期不确定水平时,按照高不确定水平(σ1=0.8)制订计划能够获得鲁棒性更强的调度方案。将这一结果与表3和表4对比可知:不考虑资源转移时间的RCPSP调度决策通常更为保守,按照高不确定水平制订计划时在项目活动之间预留了更多的时间缓冲,故而可以更有效地应对活动拖期风险。

5 结束语

本文针对带资源转移时间的RCPSP问题,考虑活动工期的不确定性,分别从资源转移关系、活动时差、随机活动工期三个不同角度设计了3种解鲁棒性衡量指标,构建了MinTPC、MinEA、MaxPF和MinTPC+MaxPF多个RCPSP-TT鲁棒调度与资源分配集成优化模型,并分别提出了模型求解方法。通过仿真实验对各方法所得项目方案的鲁棒绩效进行对比分析,实验结果表明,混合优化策略MinTPC+MaxPF能够得到解鲁棒性和质鲁棒性均最优的调度方案。研究工作延伸了资源受限项目调度的问题领域,也进一步丰富了鲁棒项目调度研究的内容,扩充了资源流网络优化在项目调度领域的应用。

本文研究旨在工期不确定条件下实现RCPSP-TT问题解鲁棒性最强的单目标优化,实际中还有很多方面因素和领域问题需要考虑,比如资源不确定环境、多目标优化(如资源转移成本、现金流、资源均衡等目标)、活动可拆分、多模式(时间-资源权衡)等,这些问题值得进一步探索研究。此外,未来有必要结合RCPSP-TT实践问题开展应用研究,将研究成果应用于基础设施建设、工程建筑、大型复杂产品制造与装配等行业,从而验证所提模型方法的实际效果,并进行评估与反馈改进。

致谢

感谢席勒·耶拿大学(Friedrich Schiller University)Armin Scholl教授为本研究提供了RCPSP-TT问题项目例库。