金属切削仿真的驱动模型及其耦合机制研究

郭必成,王福增,黄 辉,姜 峰+

(1.华侨大学 制造工程研究院,福建 厦门 361021;2.高性能工具全国重点实验室,福建 厦门 361021)

0 引言

数值仿真是一种对具体物理过程进行简化并建立其数学模型,用数学模型在计算机上进行试验和研究的方法。数值仿真技术不仅可以节约时间和成本,还可以直观展示一些试验中观测不到的现象,如利用数值仿真可以看到切削实验时无法观测到的刀具和切屑表面温度分布以及刀具磨损等情况[1-2],另外发生在物体内部一些观测不到的现象也可以在数值仿真中直观展现出来,如切削区的绝热剪切以及位错密度的演变等现象[3-4]。随着中国制造业的大力发展,金属切削技术面临着巨大的挑战。传统的切削工艺试验需要占用大量的人力、物力,消耗大量的时间,成本高、效率低,给企业造成很大的负担;并且,切削试验研究结果缺乏普适性和实时性[5],已经无法满足现代切削技术的发展。将数值仿真技术应用到金属切削过程的模拟中,大大促进了金属切削技术的发展。近年来,数值仿真技术在金属切削加工中的应用越来越广泛[6]。利用数值仿真技术,不仅可以研究不同材料的加工机理,还可以优化工艺参数[7-8]、刀具几何结构[9-12]等参数,另外还能对加工工况进行预测[13-15]。随着计算机硬件性能的提升和数值仿真软件算法的提升,数值仿真技术在金属切削过程的模拟方面发挥着越来越重要的作用。金属切削过程是工件和刀具相互作用的过程。利用数值仿真来模拟金属切削过程,首先要建立刀具材料和工件材料的本构关系,来反映材料变形、温度和应变率等之间的关系,另外还要设定好边界条件、刀具与工件的接触关系、相对运动关系及相关工艺参数等。由于切削过程的复杂性导致切削仿真的建模也具有很大的复杂性,需要考虑工件材料特性(动态力学性能、热物理属性)、摩擦润滑(界面条件)、刀具材料(基体材料、涂层材料和刀具几何角度)、装夹和机床动态特性(刚度和阻尼)、工件初始状态等,这些都需要以计算机能够识别的模型形式在仿真中体现,才能得到一个相对准确的仿真结果。

数值仿真技术的发展促进了加工过程数值仿真的繁荣,同时也会造成仿真方法及其模型的混乱和误用,对不同材料,在不同去除尺度下去除机理的不同理解会造成仿真结果的巨大差异。仿真是在计算机或实体上建立系统的有效模型,并在模型上进行系统实验的过程。按照系统论的观点,模型是一个系统(实体、现象、过程)的物理的、数学的或其他逻辑的表现形式。仿真模型是建模者对建模对象为满足仿真应用需求而建立的,以计算机语言、实体模型的物理实现等形式给出的描述[16]。因此,仿真的精度主要取决于仿真模型是否精确。同时,因为仿真模型是根据建模者的应用需求而建立的,所以仿真模型只适用于一定的工艺参数范围内[17]。在切削仿真中,仿真模型一般都是基于一定的应变率、温度和应变范围内的试验结果而建立的,因此仿真模型只在一定范围内适用[18-19],当切削过程的应变率、温度和应变远超这个范围时,切削仿真结果的准确性是没有保障的。金属切削所涉及的应变和应变率的大小比常规材料拉伸和压缩测试产生的应变和应变率高几个数量级。因此,用常规的拉伸和压缩试验建立的材料本构模型来模拟切削过程是不准确的,这是因为材料在不同的应变速率和温度下表现出不同的应变硬化和软化特性[20]。另外,材料的本构模型切削过程中材料的变形与断裂都是大变形、大位移、非线性的情况,在用有限元仿真模拟切削过程时,除了温度软化项[21-22]、应变强化项[23]和应变率强化项[24]的影响,毛坯成型的取向[25]、材料的组织转变[26-27]、材料变形机理[28-29]以及研究的尺度[30]等问题也会影响仿真的准确性。仿真的精度除了取决于仿真模型,还与仿真模型的耦合效应密切相关,因此要提高仿真的精度,不仅要研究仿真模型对仿真精度的影响,还要深入研究仿真过程的模型耦合效应及其稳定性,从而通过仿真获得准确的切削状态,提高切削仿真的可信度,有助于切削机理的研究,同时让切削仿真尽可能地替代切削试验进行工艺优化、刀具几何优化等一系列的工作。

1 金属切削数值仿真机制

金属切削数值仿真过程当中涉及很多模型,有摩擦模型、本构模型和热物理属性模型等,这些模型的迭代和耦合过程如图1所示。在仿真过程中,确定了刀具和工件的几何模型、边界条件以及初始条件后,基于运动学和动力学原理,刀具和工件相互作用,工件材料发生变形产生应变,同时根据相关条件计算得到应变率和应变的分布。伴随着应变的产生,材料内部产生应力,而应力受摩擦模型和本构模型的影响,这两个模型是应变率和应变与应力之间的桥梁。应力从两个不同形式转变为宏观物理量,一种形式为切削力,另一种形式为热量,热量也分为两个部分,其中一部分为切削环境(切削液、空气等)引起的热量损失,干切削时这部分热量损失可以忽略不计;另外一部分为传递到工件和刀具上的热量,而热量在刀具和工件上的分配是由刀具和工件材料的热物理属性决定的。热量以温度的形式宏观体现,温度升高引起本构模型和摩擦模型的变化,使应力减小,从而减少了热量产生和温度升高的驱动力,形成热-力耦合现象及算法上的迭代过程。当热-力耦合达到平衡后,切削仿真过程达到稳态,迭代过程结束并输出切削力、切削温度和切削变形等切削过程物理量的结果。这里可以发现,稳态切削力并不参与数值仿真计算的耦合和迭代过程,只是一个最终输出物理量。

切削数值仿真过程存在着大量的耦合和迭代,模型参数或网格参数的一个“小波动”,往往会在最后的仿真结果(切削力、切削温度等)中体现为一系列的连锁反应。模型参数或网格参数的稳定性问题与控制系统的鲁棒性问题,其本质上是一样的。可以将控制系统鲁棒性的成熟解决方案引入数值仿真过程中,将极大地提升仿真结果的稳定性。

2 切削仿真的驱动模型

切削仿真的驱动模型是切削系统中的内在动力是保障切削系统稳定运行的重要条件。如图2所示,切削仿真的驱动模型主要包括材料本构模型、热物理属性模型以及摩擦模型。驱动模型是切削过程中应力、应变、温度等物理量相互转换的桥梁。

2.1 材料本构模型

工件材料的本构模型本质上是材料的应力-应变曲线,材料存在应变率强化效应、应变强化效应和温度软化效应。本构模型为应力与应变、应变率和温度的关系,典型的数学表达式为Power Law本构模型:

(1)

g(εs)=σ0(1+εs/ε0)1/n,

(2)

(3)

Θ(T)=C0+C1T+C2T2+C3T3+C4T4+C5T5,

(4)

T=T0+ΔT。

(5)

本研究选择的工件材料为Fe-Cr-Ni不锈钢,前期笔者课题组建立了Fe-Cr-Ni不锈钢的本构模型如式(6)所示[31]。

(6)

2.2 材料热物理属性模型

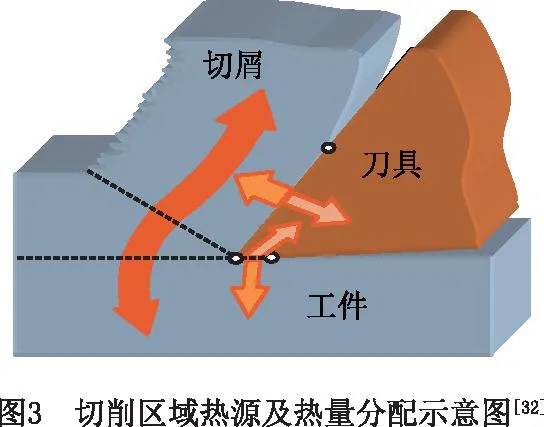
热物理属性模型决定了热量在刀具、切屑和工件中分配的比例,热量产生和分配示意图如图3所示[32]。热物理属性主要包括比热容和热导率,比热、热导率和密度是表征容热能力的重要指标。并且材料的热导率和比热容不是恒定不变的,是随温度实时变化的,材料在不同温度下的热物理属性模型参数可利用激光热导仪测定。前期笔者课题组测得Fe-Cr-Ni不锈钢的热物理属性结果如图4所示[33],热物理属性模型如式(7)～式(9)所示。切削过程刚开始阶段,比热容和热导率随温度的升高而升高(如图4),而比热容和热导率的升高会减弱切削温度上升的趋势,抑制切削温度的升高。当切削温度达到某一值时,Fe-Cr-Ni不锈钢的热导率和比热容都随温度的升高而降低,这会加速温度的上升趋势,这个效应与应变强化都会使切削温度升高,两者的综合效应与温度软化效应交互作用,最终达到一个平衡。

Cp=0.3746+4.8492e-5T+6.1368e-7T2,

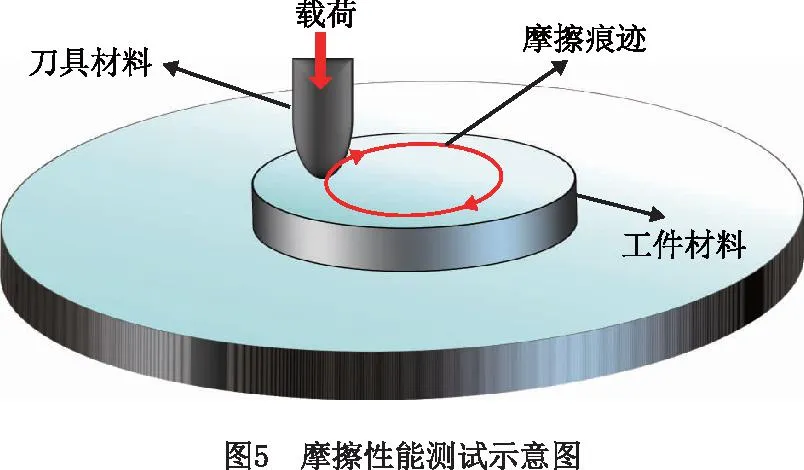
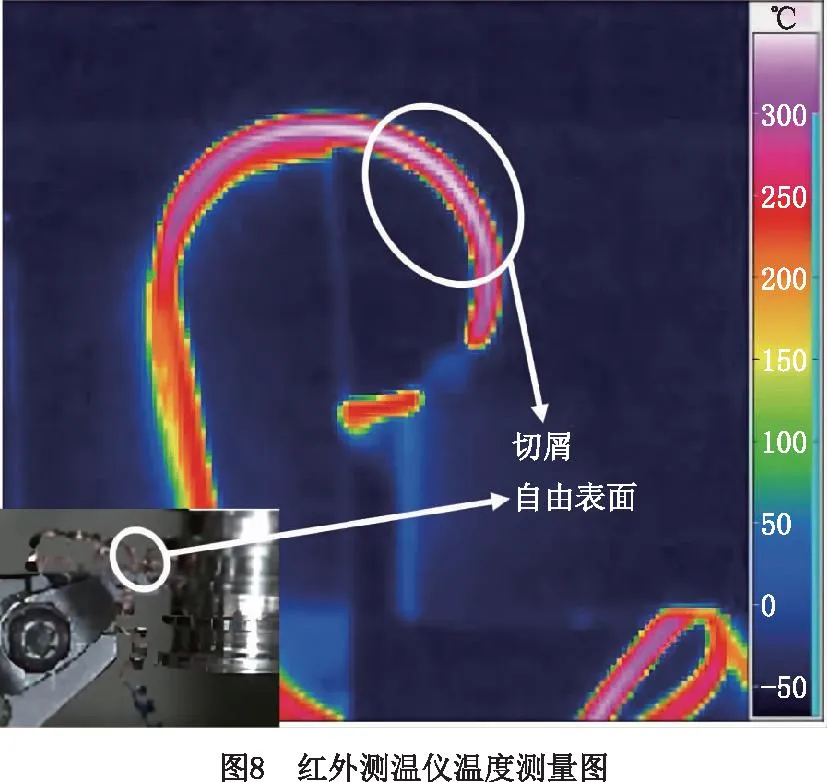
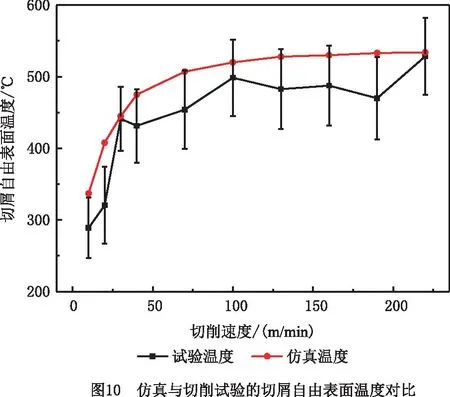
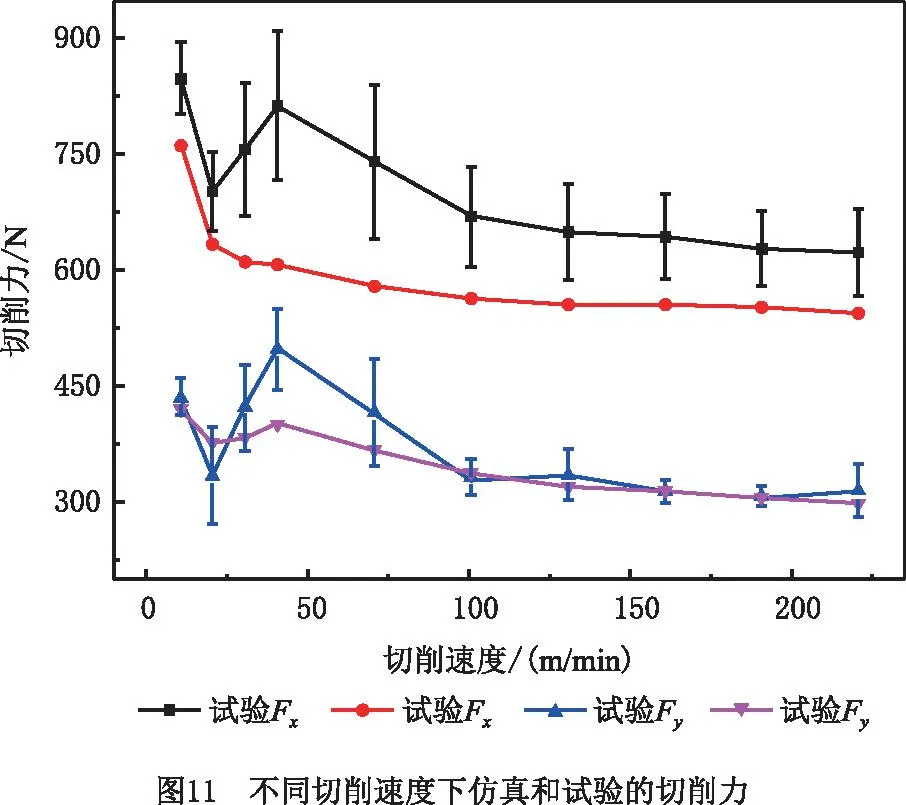
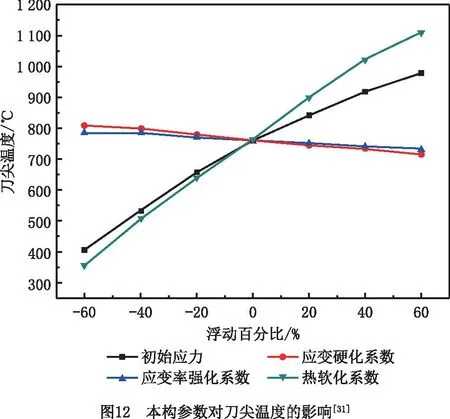
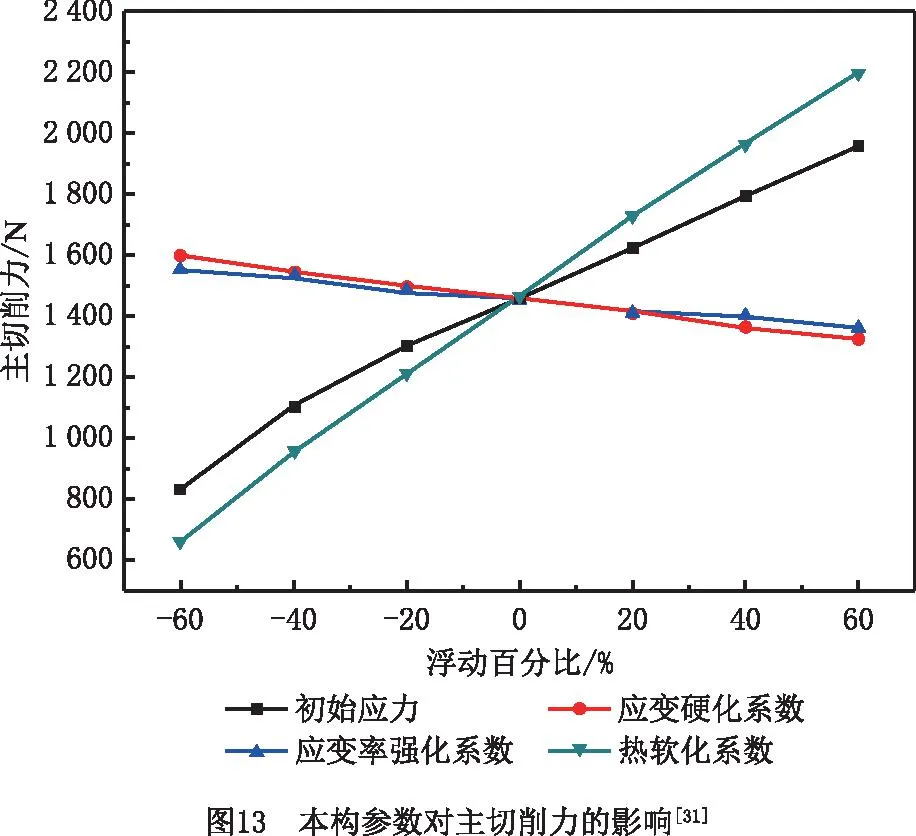
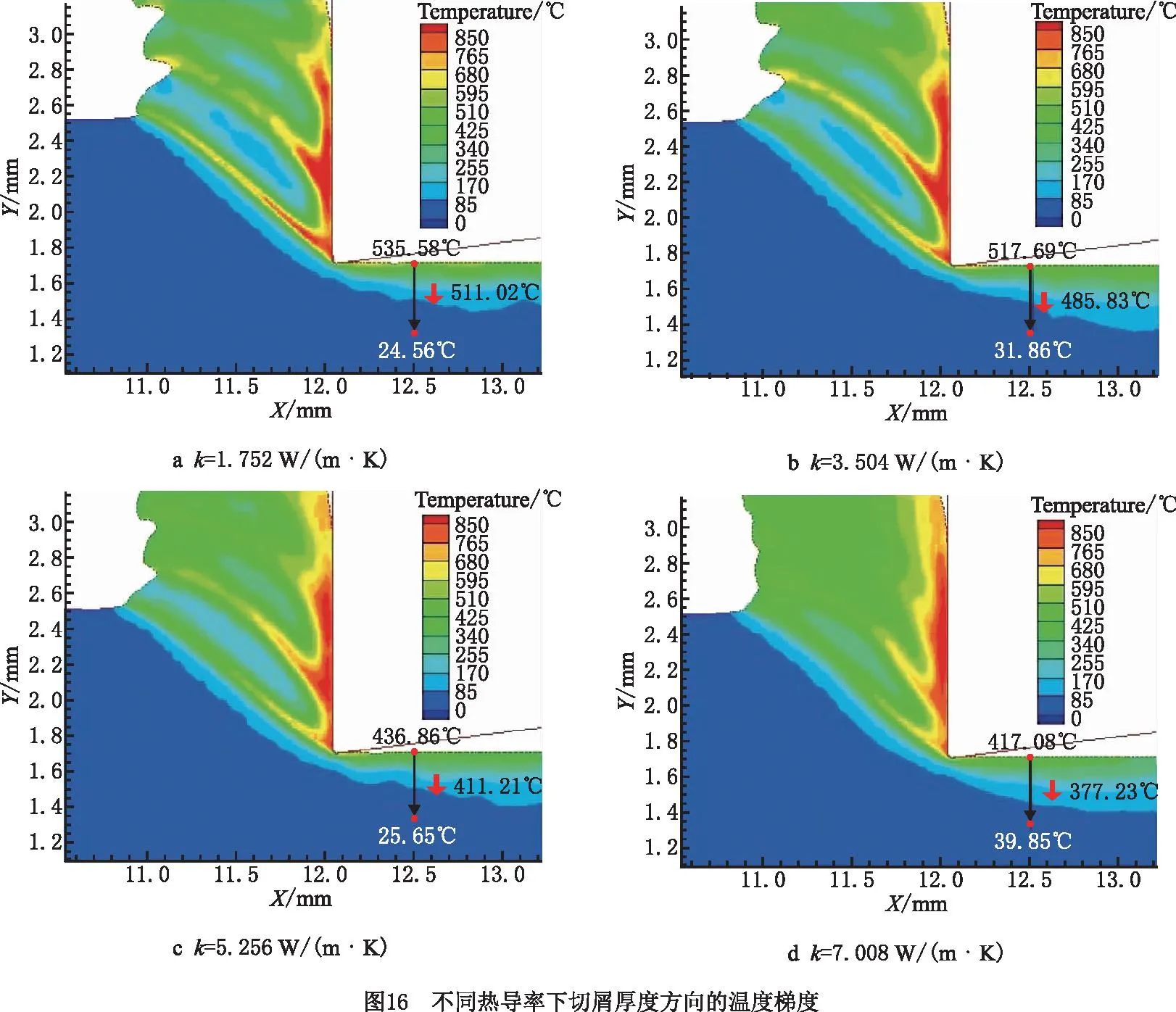
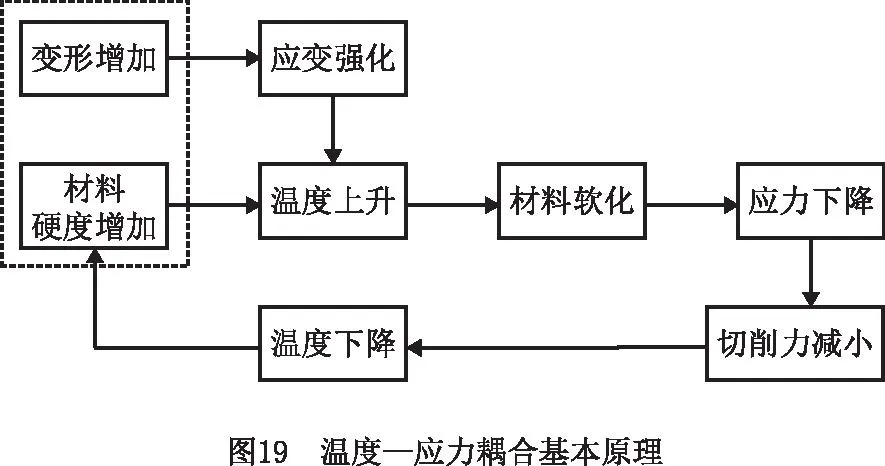
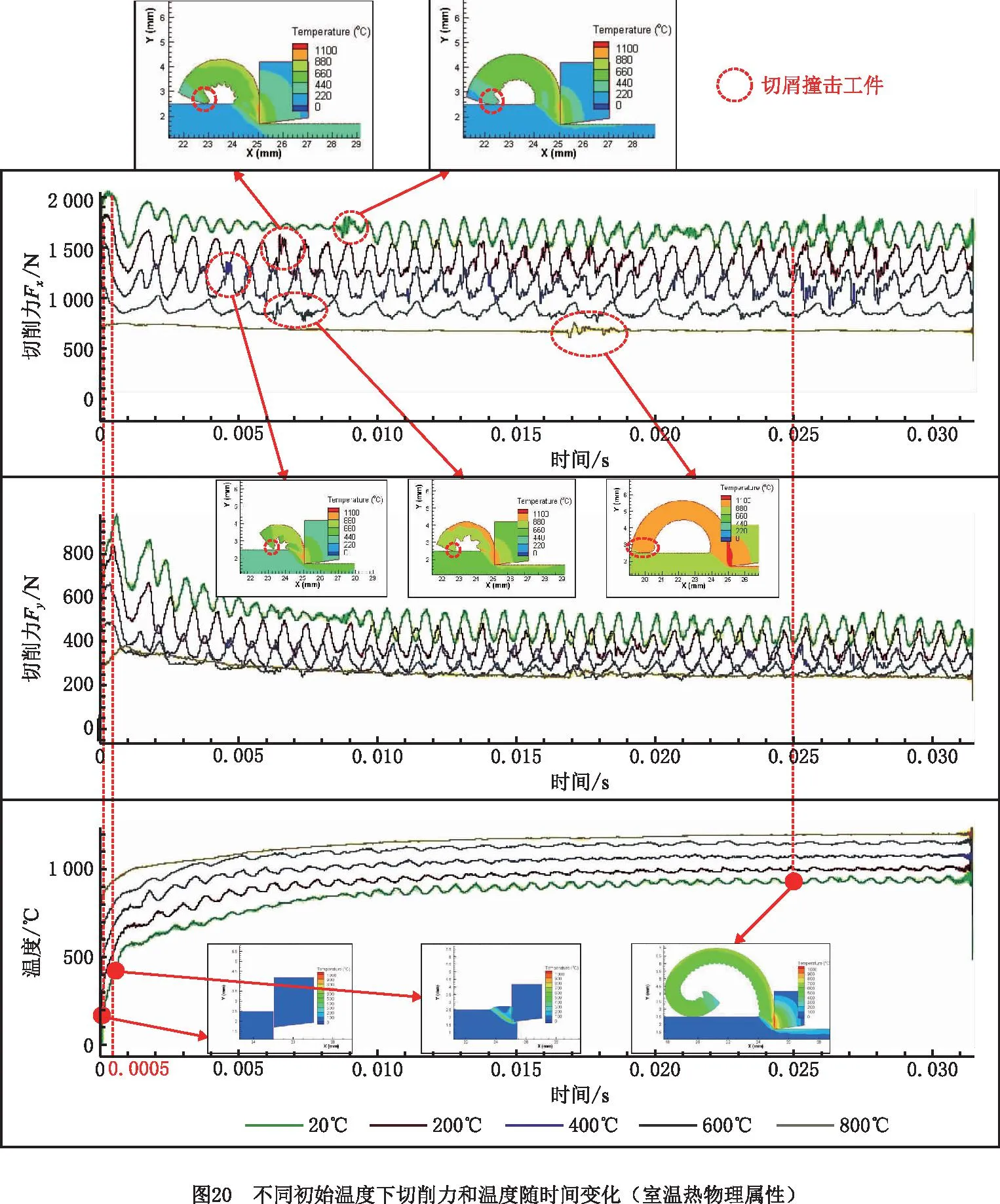
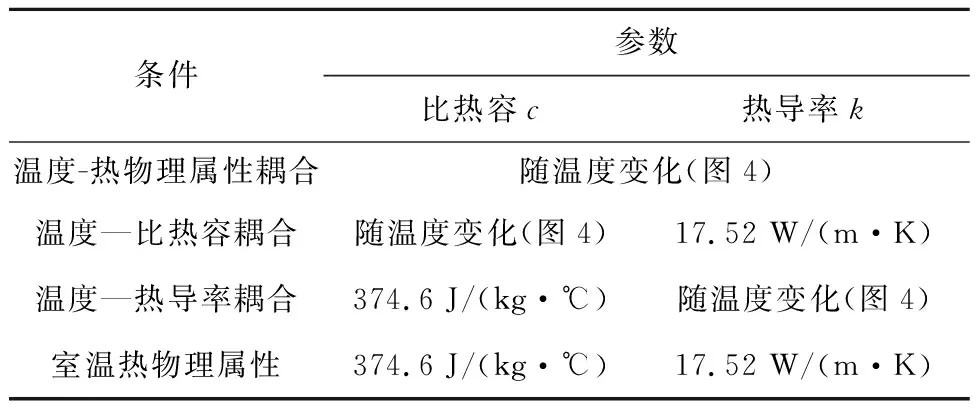
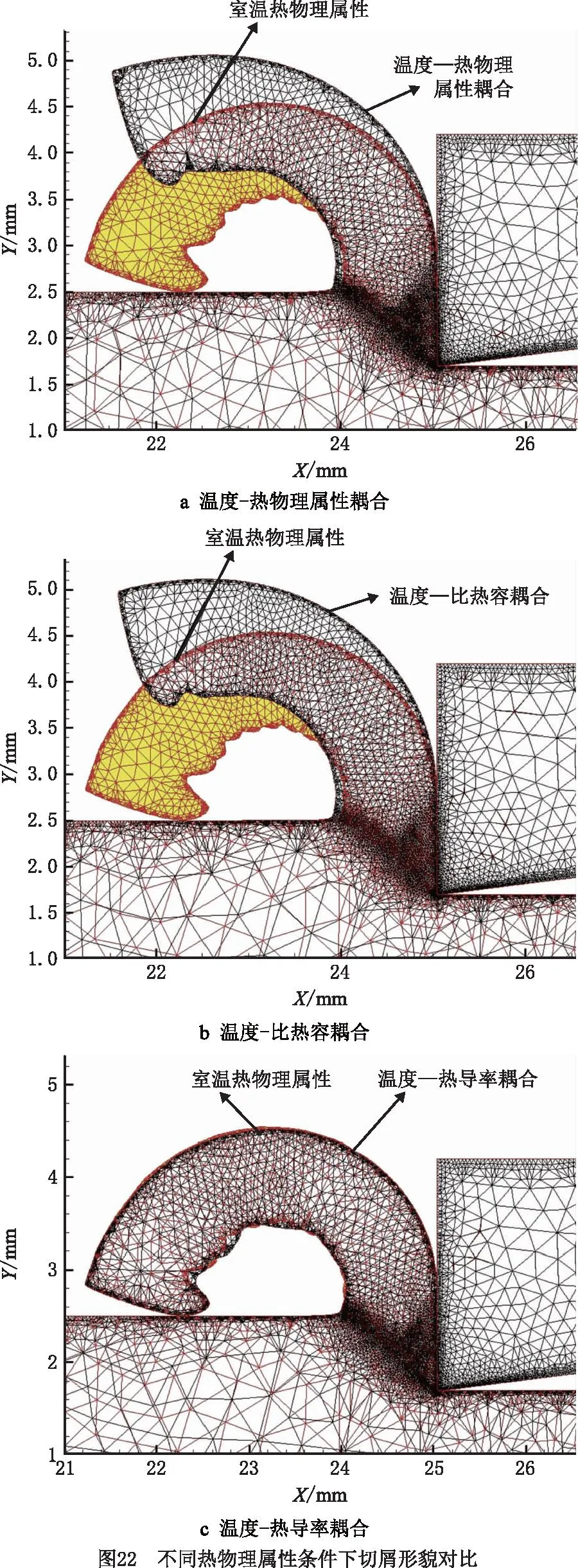
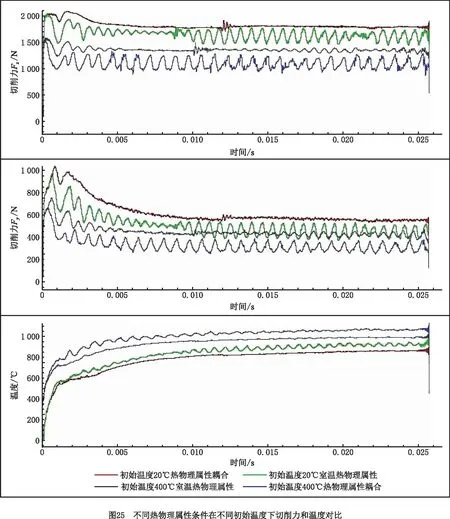
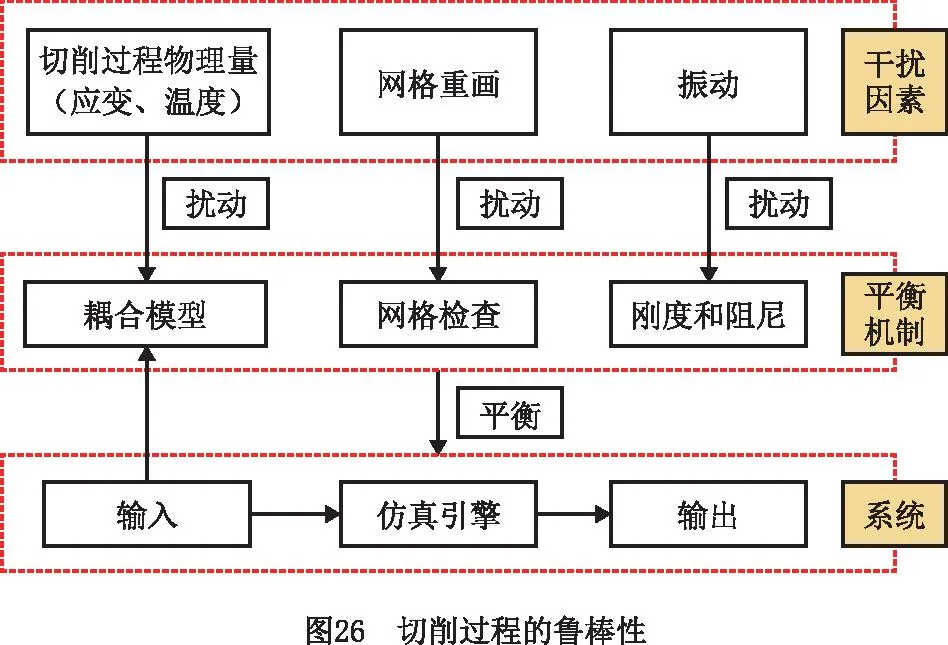
20 ℃

(7)

Cp=2.6061-4.1607e-3T+1.9122e-6T2,

600 ℃

(8)

k=17.5201+1.9641e-2T-1.1294e-5T2,

20 ℃

(9)

其中:Cp为材料的比热容;k为材料的导热系数;T为温度值。

2.3 摩擦模型

根据库伦定律,摩擦力为摩擦系数和正压力的乘积。为了减小切削过程不确定因素的影响,更好地研究工件-刀具间的摩擦特性,使用美国CETR公司的UMT-2高温摩擦磨损试验机研究滑动摩擦系数,球盘摩擦试验中工件材料-刀具材料的接触状态与切削试验中刀具前刀面-工件材料的接触状态是相近的[34],测试示意图如图5所示。

试验的滑动线速度分别设为10 m/min、20 m/min、30 m/min、40 m/min、70 m/min、100 m/min、130 m/min、160 m/min、190 m/min、220 m/min,试验条件为干摩擦,以得到不同滑动速度下的摩擦系数;垂直载荷恒定,设为4 N。试验得到的平均摩擦系数随滑动速度变化的曲线如图6所示,数据拟合得到摩擦模型如式(10)和式(11)所示,适用于干切削。受滑动速度影响的平均摩擦系数模型可以作为切削数值仿真的输入条件,考虑速度对摩擦系数的影响,仿真模型更加精确。

μ=3.1059e-3v+0.475,10

(10)

μ=-8.7868e-8v3+4.5608e-5v2-7.6329e-3v+

0.8992,40

(11)

其中μ为摩擦系数,v为滑动线速度。

3 试验验证方法

本研究进行了直角车削实验,测量车削力和车削温度,用来验证切削过程数值仿真建模的准确性。工件材料预切了许多沟槽来实现直角车削,沟槽的宽度就是切削宽度aw,如图7所示。车削工艺参数与切削数值仿真的设定参数保持一致。本研究进行的实验均为干切削,空气的冷却作用有限,因此忽略切削过程中的对流和辐射现象。为了保证实验系统的刚度和切削稳定性,利用DAEWOO V500加工中心进行试验,测力仪为Kistler 9441车削测力仪,主要测量主切削力Fx和吃刀抗力Fy,主切削力Fx垂直于刀具基面,吃刀抗力Fy与工件轴线方向相垂直,与进给方向平行,如图7所示,试验现场测温如图8所示,测温仪器为InfraTec ImageIR红外热像仪,其温度的测量范围为-40 ℃～1 200 ℃,热灵敏度为0.025 K。工件材料为Fe-Cr-Ni不锈钢,其模型参数如式(6)所示。刀具为肯纳的NSR 2020K3切断刀柄,刀柄前角、刃倾角均为0°。刀片为NG31系列切断刀片,刀片的前角分别为0°,后角均为7°,刃口半径约为18 μm。刀具仅作径向进给,进给量为每转0.1 mm,车削速度分别设定为10 m/min、20 m/min、30 m/min、40 m/min、70 m/min、100 m/min、130 m/min、160 m/min、190 m/min、220 m/min。

由于切屑对刀-屑接触区域的阻挡,红外测温仪很难测得切削区的最高温度,靠近刀尖的刀-屑接触面的温度也是难以检测到的,往往红外测温仪测得的是切屑自由表面的最高温度(如图8),为便于仿真与实验结果的对比,仿真的切屑自由表面最高温度和切削区域最高温度都被提取出来(如图9),测量结果如图10所示。

(12)

式中:error为误差,x1为仿真结果中物理量的值,x2为切削试验中物理量的值。

如图10和图11所示,由切削试验和仿真结果以及式(12)可知,在该试验条件下,仿真和切削试验的结果误差较小,其中主切削力的误差在9.7%～25.4%之间波动,平均误差为15.56%。吃刀抗力的误差在0.3%～19.3%之间波动,平均误差为3.86%。切屑自由表面温度的误差在0.9%～27.3%之间波动,平均误差为10.34%。因此,本研究的仿真模型是相对精确的。

4 仿真模型参数对仿真结果的影响

4.1 本构模型参数对仿真结果的影响

笔者课题组利用Fe-Cr-Ni不锈钢的仿真模型研究了本构参数对切削过程中物理量(温度、切削力、切削变形等)的影响。仿真软件为AdventEdge FEM,工艺参数:初始温度T=20 ℃,切削速度v=40 m/min,切宽aw=1 mm,仿真进给量f=0.6 mm/r;刀具参数:前角γ=0°,后角α=7°,刃口半径r=0.06 mm;刀具材料选用硬质合金,本构模型参数的值以式(6)中应变硬化系数n、应变率强化系数m等参数的标准值为基准值,上下浮动固定的比例获得,如表1所示[31]。

表1 本构模型参数浮动表[31]

如图12所示为本构模型中4个参数对刀尖温度的影响变化曲线。随着初始应力和热软化系数数值的增加,刀尖温度逐渐增大,而随着应变硬化系数和应变率强化系数的增加,刀尖温度逐渐减小。由曲线的斜率得知,对刀尖温度影响强弱的顺序是C0>σ0>n>m[31]。同理,如图13所示,热软化系数、初始应力、应变硬化系数和应变率强化系数对主切削力和刀尖温度的影响效果是一致的[31]。

切屑是衡量金属切削过程的又一重要指标。由图14可知,初始应力和热软化系数对切屑卷曲有显著的影响。随着初始应力和热软化系数的增加,切屑卷曲半径逐渐减小,并且初始应力对结果的影响增大。随着应变率强化系数和应变硬化系数的增加,切屑卷曲半径逐渐增大[31]。

4.2 热物理属性参数对仿真结果的影响

为验证热物理属性参数对仿真结果的影响,本研究利用AdvantEdge软件建立二维切削仿真模型,将网格划分等级设置为0.5,网格细化因子和网格粗化因子分别设置为2级和6级;最大网格尺寸设置为0.1 mm,最小网格尺寸设置为0.02 mm。材料本构模型如式(6)所示,热物理属性参数如表2所示,工艺参数:切削宽度aw为1 mm,进给量f为0.8 mm/r,切削速度v为40 m/min,本构模型如公式(6),摩擦系数为默认值0.5,刀具前角γ=0°,后角α=7°,刃口半径r=0.018 mm;刀具材料选用硬质合金,仿真结果如图15和图16所示。

表2 热物理属性参数设置

在切削速度等其他参数不变的情况下,加工产生的热量是相同的,比热容c越大,温升就越小,切削温度越低。同时,根据热力耦合原理,温度越低,工件材料越硬,因此随着比热容c的增加,切削力和切削应力将增大,如图15所示。另外,还可以看出比热容c对切削过程中锯齿切屑的形成有显著的影响。比热容c越小,切屑的锯齿状越明显,主切削力的波动也越明显。比热容c主要影响切削温度、切屑形态以及主切削力,对吃刀抗力影响较小。

热导率k决定了温度的梯度,热导率k值越大,材料的热传导性能越好,保温性能越差,其温度梯度越小,如图16所示,由于切削区域的产热区包括剪切区和摩擦区域,切削区和切屑区域的传热是相互干扰的,选择已加工区域的温度做对比。如图16所示方向,已加工区域的温度梯度随材料热导率的增大而减小。

4.3 摩擦系数对仿真结果的影响

由摩擦性能试验可知,刀具和Fe-Cr-Ni不锈钢工件之间的摩擦系数μ在0.5附近波动。本研究分别设置摩擦系数μ为0.1,0.2,0.3,0.5,0.7,0.9的6组仿真试验来研究摩擦系数对切削过程的影响。热物理属性模型参数如式(7)～式(9)所示,其他试验条件与4.2节一致。仿真试验结果如图17和图18所示,当0.1<μ<0.3时,随着摩擦系数μ的增大,刀-屑之间的摩擦力将增大,切削力也随之增大,切削温度逐渐增大。当μ>0.3时,随着摩擦系数μ的增大,切削力及切削温度的变化都变化很小,切屑的形态也相差很小,此时摩擦系数对切削过程的影响很小,而实际测得摩擦系数的值为0.5附近波动,因此进行仿真试验时,可设置摩擦系数为0.5。另外,从图18中切削力的波动可以看出,摩擦系数越大,切削过程达到稳态需要的时间越长,因此切削仿真的平衡过程需要足够的仿真时间。在进行切削仿真时,需要设置足够的切削长度及切削时间,使切削过程达到稳态,从而分析稳态切削过程的数据。总之,μ在0.1～0.9之间变化时,切屑卷曲半径在1.36 mm～1.75 mm之间波动(切屑卷曲半径为内外半径的平均值);主切削力的变化范围为1 635 N～1 811.53 N;吃刀抗力的变化范围为244.63 N～539.88 N;切削温度的变化范围为599.1 ℃～883.36 ℃。摩擦系数主要影响吃刀抗力、切削温度以及切屑卷曲半径。

5 模型驱动的仿真原理中的耦合

5.1 温度-应力耦合

金属切削过程数值仿真有一个核心耦合:温度-应力耦合(热-力耦合)。热-力耦合,即应力场与温度场两个物理场之间相互影响的过程,该过程主要与材料本构模型相关。为了分析切削仿真原理中各模型之间的耦合,本研究开展了5组切削仿真试验。为了避免热物理属性耦合对热力耦合的影响,将Fe-Cr-Ni不锈钢的比热容及热导率分别设置为常温下的值,设置不同的初始温度研究温度-应力耦合过程,参数如表3所示,其他试验条件与4.2节一致。

表3 温度-应力耦合试验参数设置

切削过程中,刀具与工件相互作用,工件材料发生形变,随着变形的增加,工件材料将发生应变强化,切削温度逐渐升高,使材料发生软化,切削力降低,从而温度降低,材料的硬度会增大再次导致温度的上升(如图19)。在应变强化和热软化的交互作用下,切削过程逐渐达到平衡状态。

由图20可以看出,在切削时间t≤0.000 5 s时,温度较低,应变强化效应强于温度软化效应,此时切削力和温度均逐渐增加;在切削时间t>0.000 5 s时,温度较高,温度软化效应强于应变强化效应,切削区材料变软,切削力逐渐减小,产热也逐渐减少,温度上升缓慢,最终达到一个稳定的状态。所谓稳态,就是平衡状态,即热软化和应变强化达到平衡,要达到这个平衡,有限元程序需要多次的迭代,而耦合的迭代过程主要受到热物理属性模型的控制。同时,仿真的时间要足够长,保证仿真结果达到稳态。另外,切削过程中刀具与工件的相互作用,使刀具前刀面与切屑、刀具后刀面与工件都存在摩擦与挤压的作用。刀具与切屑、刀具与工件的摩擦作用,同样会使切削温度升高,从而影响温度、应力、应变等物理量的耦合过程。在耦合过程中,温度是一个至关重要的物理量,它对仿真的稳态进行影响显著。由图20可知,初始温度越高,切削过程更易达到稳态,同时初始温度越高,最终平衡温度也越高,切削力越小。

另外,切削系统具有鲁棒性。系统的鲁棒性是指系统在某种类型的扰动作用下,包括自身模型的扰动下,系统某个性能指标保持不变的能力,也就是系统达到平衡的过程。而耦合的目的就是平衡和再平衡(鲁棒性)。如图20所示,切削过程刚开始时,刀具与工件发生相互作用,材料发生变形,切削力和温度逐渐升高,由于系统的鲁棒性,当切削力达到一定程度时会略微降低并逐渐达到稳定状态;而稳定之后,随着切削长度的增加,切屑长度也不断增加,当切屑撞击到工件时,系统会受到干扰,出现波动,这时系统具有“再平衡”的功能,即在温度-应力的耦合作用下,温度和力逐渐达到平衡状态。切削仿真实现这个平衡过程,需要较长的仿真时间,因此开展仿真试验要设置时间足够长保证系统达到稳态,才能获得较稳定的仿真结果。

5.2 温度-热物理属性耦合

在切削过程中,剪切面、切屑与前刀面接触区、后刀面与过渡表面接触区会有热量的产生,但热量并不等于温度,热量转换成温度值主要与材料的比热容c和热导率k等热物理属性相关。比热容c是指单位质量物体改变单位温度时吸收或放出的热量,决定了温度的高低,热量Q=m·c·ΔT可以形象地理解为:注入水池中的总水量为热量Q,水池的底面积与比热容c成正比,则水池中水的高度h就代表了温升值ΔT(如图21所示),所以比热容c与温升值ΔT是反比的关系,如式(13)所示。绝热温升ΔT是指放热反应物完全转化时所放出的热量可以使材料升高的温度[22]。随着切削过程中温度的升高,材料的热导率和比热容随温度不断变化,实时影响着切削过程的产热和散热从而抑制温度的升高,温度和材料热物理属性不断耦合促使切削过程逐渐趋于稳定,即切削系统的鲁棒性。

(13)

式中:ΔT为绝热温升值;ρ为材料的密度;c为材料的质量热容;σ为材料的应力;ε为材料的应变,β为能量转换率,一般认为材料的塑性功全部转化为材料绝热温升,故取β=1。

如图21所示,假设切削区域的单位时间产生的热量为Q,将切削过程热传导过程比作水池进出水的过程(假设水池的池壁和底面是有弹性的),切削过程热量Q可以比作水池单位时间进水量,水池的底面积A1与比热容c成正比,排水管的截面积AL与k成正比,排水管的单位时间流量为QL,排水管的流量可以理解为切削过程中切削区域传递到刀具、切屑和空气中的热量,热导率k越大,截面积AL越大,排水管单位时间的流量越大,即切削区域单位时间内传递出的热量越多。随着切削过程的进行,切削温度不断升高,比热容c和热导率k随温度升高而变化,即水池底面积和排水管的截面积随温度升高而变化,当单位时间排水量与单位时间进水量相等时,即QL=Q时,即切削区域产生的热量与传导的热量达到平衡,从而切削区域的温度达到稳定状态。

为了验证热物理属性对切削过程的影响,设置热物理属性参数如表4和表5所示,其他试验条件与4.2节一致。

表4 热物理属性参数设置(初始温度20 ℃)

表5 不同初始温度的温度-热物理属性耦合

由图22可知,影响切屑形态的主要参数是比热容,热导率对切屑形态的影响较小,由前文可知热导率主要影响材料的温度梯度及温度传递。

如图23所示,结合图21,当比热容为室温参数时,相对于比热容和热导率为室温参数而言,温度略微降低,这是因为随温度升高,热导率升高,温度传递更快,但是热量传递速率相对于产热速率较小。当热导率为室温参数时,相对于比热容和热导率为室温参数而言,温度降低更多,切削力增大,这是因为随温度升高,比热容升高,材料吸热能力增强,抑制温度的升高,则温度更低。当比热容及热导率都随温度变化时,即温度-热物理属性耦合,随温度升高,材料性能具有抑制温度升高的趋势,与产热相互耦合,逐渐达到稳态。具有温度-热物理属性耦合与室温热物理属性参数下的仿真平衡温度差为67.05 ℃,主切削力差为190.8 N,吃刀抗力差为102.3 N。另外,对比图23中不同条件下的力和温度曲线可知,切削过程的稳定性排序为:温度-热物理属性耦合>温度-比热容耦合>温度-导热率耦合>室温热物理属性,热物理属性参数对切削过程的稳定性具有重要作用。

表5的仿真结果如图24所示,对比图20的部分结果如图25所示,相对于只有温度-应力耦合的切削过程,同时具有温度-应力耦合和温度-热物理属性耦合的切削过程鲁棒性更好,切削力及温度的波动较小,在切屑碰到工件时,也能迅速进入稳态,保持切屑过程稳定进行,不再出现波动,另外如图中标记的波动,是由于没有温度-热物理属性耦合,没有外界的干扰,系统也不稳定,易波动,而具有温度-热物理属性耦合的切削过程切削力和温度更稳定,因此热物理属性耦合是切削过程鲁棒性的一个重要作用,对切削过程的稳定性尤为重要。对比图20和图24,相同初始温度下,平衡状态时,温度差范围为50.29 ℃～70.68 ℃,主切削力差范围为126.83 N～279.89 N,吃刀抗力差范围为89.99 N～132.73 N。对比室温热物理属性与热物理属性耦合情况下不同初始温度试验的切削力和温度,如图25所示,可以看出室温热物理属性下,切削力及温度的波动较大,温度-热物理属性耦合情况下切削力及温度的波动较小,切削过程更稳定。

切削系统的鲁棒性是指在一定参数的扰动下,维持系统平衡的特性。如图26所示,影响切削仿真过程稳定的干扰因素主要包含3个方面:切削过程中的物理量、网格重画以及振动。而调节扰动,维持系统稳定的平衡机制也包含3个方面,其中网格重画主要利用仿真软件AdventEdge FEM中自适应网格划分和网格自动检查功能来调整仿真过程中的网格划分,从而保障仿真的稳定;振动主要利用软件中的刚度和阻尼命令来调节,保障仿真的稳定。本研究主要研究仿真模型的耦合作用调整切削仿真的物理量来保障切削仿真的稳定进行。即通过热-力耦合和温度-热物理属性耦合作用来实现切削系统的鲁棒性。如图1所示,热-力耦合主要体现在材料的硬度等属性随温度的实时变化,切削过程中材料变形做功产生温升使材料变软,而材料变软使材料变形做功产生的热量减少,两者相互影响来维持切削系统的平衡;温度-热物理属性耦合主要体现在热导率和比热容等属性随温度的实时变化,而热物理属性的变化会改变温升的大小和温度的分布,系统温度偏高时,会通过实时调节热物理属性的大小来降低温度,同样系统温度偏低时,会通过实时调节热物理属性的大小来升高温度。两个耦合中都是通过温度反馈来调节材料的属性,保障切削系统的稳定进行,即切削系统的鲁棒性。

6 结束语

数值仿真的精度问题,特别是切削过程数值仿真的精度问题,在未来很长一段时间都将是一个热点问题,影响着数值仿真技术的推广和应用。本文对金属切削有限元仿真的计算流程进行了系统分析,找出了影响仿真精度的关键点,总结如下:

(1)影响切削过程有限元仿真精度的输入模型有材料本构模型、摩擦模型以及材料热物理属性模型等,每个模型的参数对仿真结果的影响如表6所示。由于切削仿真模型的耦合特性,切削仿真的精度取决于所有模型中精度较差的仿真模型。因此在输入某一模型参数时,要对这个未知参数多次取值,对比不同取值条件下的仿真结果,从而确定模型参数对仿真结果的影响程度。

表6 仿真模型参数对仿真结果的影响

(2)金属切削原理与仿真的本质是一样的,都是一个自然的过程,具有鲁棒性-切削过程的性能指标保持不变的能力,即保持平衡的能力。切削过程的鲁棒性,对于金属等塑性材料,主要体现在两个耦合现象:温度-应力耦合、温度-热物理属性耦合,两个耦合分别由材料本构模型以及热物理属性模型驱动。仿真计算过程就是耦合、迭代,最终达到“平衡”的过程,“平衡”后的切削力和切削温度实现稳态输出。

(3)仿真模型的验证不仅要验证切削力,还要验证切削温度,温度是切削过程中一个重要参数。而由于切削过程中切削区域的温度难以直接测量,因此需要测量切屑自由表面温度来验证仿真结果。另外仿真结果存在大量的数据,新的试验检测技术也不断地涌现,未来仿真结果的验证会更加全面和精确,仿真技术的发展会更加迅速。