考虑可变时间的双边机器人拆卸线平衡问题建模与优化

脱 阳,张则强+,张 裕,郑红斌,梁 巍

(1.西南交通大学 机械工程学院,四川 成都 610031;2.轨道交通运维技术与装备四川省重点实验室,四川 成都 610031)

0 引言

中国制造2025[1]提出了五大工程,其中绿色制造与智能制造工程更是重点工程,两者密不可分。绿色制造[2]是以环境影响和资源消耗为要点的现代制造模式,目标是使产品在整个生命周期中达到最大化资源利用率,最小化环境负面影响,协调优化企业经济效益和社会效益。智能制造[3]是可持续发展的制造模式,通过建模仿真和信息通信技术的力量来优化产品的设计和制造过程,大幅度减少各类资源和能源消耗,同时实现保护环境和循环再用。拆卸是绿色制造过程中的重要组成部分,通过从废弃产品中选择性分离所需的组件、零件和材料进行回收和再利用,实现再制造[4]。工业机器人作为先进制造业中典型的机电一体化数字化装备,提高了加工效率与产品一致性。在拆卸作业中选择机器人进行拆卸能够很好地将绿色制造和智能制造结合[5],因此本文针对机器人拆卸展开研究。现有拆卸企业为降低拆卸成本、提高拆卸回收效率,拆卸过程常采用生产线的方式进行,但是拆卸任务分配不均会降低生产效率,增加成本。为此,GUNGOR等[6]提出了拆卸线平衡问题(Disassembly Line Balancing Problem,DLBP)。

传统拆卸线以单边和U型为主[7],这类拆卸线面对某些大型废旧产品,如汽车、冰柜等,由于工作站位置固定,在拆卸具有方向约束的部件时难以改变其方向,从而无法完成某些任务,严重影响拆卸效率,故对这类产品往往采取双边拆卸形式。邹宾森等[8]建立了双边拆卸线的概念模型,并使用蝙蝠算法对电冰箱拆卸实例进行了验证;谢梦柯等[9]改进了考虑能耗及工位约束的双边拆卸线模型,采用改进差分算法对问题进行了验证。以上研究未考虑将拆卸问题与机器人结合。LIU等[10]提出机器人拆卸线模型,设计了一种多目标离散蜂群算法来解决拆卸线平衡问题;YIN等[11]建立了多机器人工作站多产品部分拆卸线模型,研究了多机器人同时拆装的部分拆卸线平衡问题,并提出一种多目标混合驱动算法来解决。以上研究中机器人类别单一且位置一旦固定便不再调整,设备安排缺乏柔性。本文从实际问题出发,根据拆卸任务及优化目标,考虑在采用不同类别机器人适配不同任务的情况下带来的时间变化问题。不同类别机器人拆卸相同任务时,拆卸时间不同[12]。如一型号机器人拥有更高的传动效率、传动精度、平均寿命以及定位精度,通过对相同任务采用不同机器人拆卸进行多次比较测试发现,一型机器人相较于三型机器人,定位识别速度更快,抓取时更精准,失误率更低,导致拆卸时间更快。因此选择一型机器人处理危害任务,能够有效减少危害任务的拆卸时间,从而减少危害任务对机器人的损坏。基于此,本文考虑一种根据站内任务属性分配不同机器人到组合工作站的拆卸线问题,拆卸线时间会根据站内机器人型号发生变化,一型机器人拆卸相同任务时时间最短,二型次之,三型最慢。同时考虑实际拆卸过程中选用不同型号机器人引起的能源消耗问题,以此来降低成本,提高拆卸效率。

传统求解DLBP问题的方法有精确求解法和启发式算法,但这两种方法随着拆卸任务的增加会产生组合爆炸问题。为了解决大规模DLBP问题,智能算法开始被使用。曾艳清等[13]提出一种Pareto花授粉算法解决多目标斗链式混流拆卸线平衡问题;ZHU等[14]使用混群领域搜索算法对多目标部分平行拆卸线问题进行了求解。樽海鞘群算法(Salp Swarm Algorithm,SSA)是澳大利亚学者MIRJALILI等[15]在2017年提出的一种新型群智能优化算法,该算法模拟了海洋动物樽海鞘的群体觅食行为,机制简单易懂,操作方便,易于实现,已经成为国内外很多学者的研究热点。如SUN等[16]利用改进的樽海鞘群算法(Improved Salp Swarm Algorithm,ISSA)解决车间调度问题;ASASI等[17]提出一种解决同步最优分布式发电机新技术,利用SSA优化得到最佳解决方案。目前尚未有将樽海鞘群算法应用于求解DLBP问题的公开报道,因此将SSA算法引入拆卸线平衡问题研究中,但是SSA算法迭代中会出现局部最优的问题,所以引入莱维飞行策略并结合Pareto思想及拥挤距离机制,提出一种改进的樽海鞘群算法。

本文根据多型号机器人对不同属性任务拆卸时间的改变问题,建立了以最小化工作站数、工作站空闲指标、危害指标及机器人能耗指标的多目标双边拆卸线平衡问题(Two-sided Disassembly Line Balancing Problem,TDLBP)数学模型,提出一种ISSA算法,将算法与经典案例和双边拆卸案例进行对比,验证其有效性和可行性;最后通过废旧汽车拆卸实例计算分析,与实际问题相结合。

1 双边机器人拆卸线的数学模型

1.1 问题描述

双边拆卸线是在传送装置的左右两侧分别设立拆卸工作站,左右两边工作站组成一个组合工作站,如图1所示,待单一拆卸产品从传送带输入端进入,根据节拍时间依次在各个组合工作站之间停留,左右两个工作站则根据分配的拆卸任务对产品进行拆卸[18]。如图2所示为8任务拆卸优先关系图,圈内数字表示拆卸任务编号,上方对应该任务的拆卸方向。以任务8为例,其紧前任务为5、2、6,紧后任务为7,拆卸方向为E。只能在左边进行拆卸的任务记拆卸方向为L;对于只能在右边进行拆卸的任务记拆卸方向为R;对于两边都可以进行拆卸的任务记拆卸方向为E。双边拆卸在解码过程需要遵循组合工作站站内时间约束。分配拆卸任务时,应避免拆卸任务皆分配至组合工作站同一侧,而是将拆卸任务均匀分配至组合工作站的两侧。

每当任务填满工作站,根据站内任务属性选择适宜机器人加入工作站,同时减少分配至该工作站内的任务拆卸时间,重新分配此工作站内任务,直到再次填满。任务属性分为需求和危害属性,部分任务兼具两种属性。将对环境、人体、机器人有害的零件定义为危害零件,将再利用、回收价值属性高的零件定义为需求零件。为满足绿色制造与智能制造要求,具有两种属性的零件一般需要优先拆除。

为了方便双边拆卸线模型的建立,提出以下问题假设:

(1)各拆卸任务之间作业互不干扰。

(2)拆卸供给无限量,且拆卸过程不中断。

(3)拆卸为完全拆卸,每个任务都要得到分配。

(4)不考虑产品移动时间。

(5)忽略其他突发情况。

(6)拆卸产品为单一产品且损坏程度相同。

(7)机器人对所有拆卸任务均具有适配性。

1.2 数学模型

i,j,s表示拆卸任务编号。

m表示组合工作站编号。

z表示机器人型号。

I表示拆卸任务集合,|I|=n。

M表示组合工作站数集合。

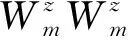
Umk表示第m个组合工作站的第k边,若开启,则Umk=1,否则Umk=0。

k表示组合工作站的边,k=1为左边,k=2为右边。

ximk表示任务i分配至第m个组合工作站的k边。

yismk表示若任务i,s皆分配至第m个组合工作站的k边,当任务i先于s分配至该工作站内时记yismk=1,否则yismk=0;当任务s先于任务i分配至该工作站内时记ysimk=1,否则ysimk=0。

BTimk表示分配在第m个组合工作站k边的任务i的起始作业时刻。

FTjmk表示分配在第m个组合工作站k边的任务j的截至作业时刻。

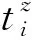
Riz表示任务i由机器人z拆卸,若为机器人z拆卸,则Riz=1,否则,Riz=0。

CT节拍时间。

di表示拆卸任务i的需求指标,若有需求,di为i的需求指数,否则di=0。

hi表示拆卸任务i的危害需求指标,若既有危害又有需求,则hi=1,否则hi=0。

nL表示左侧拆卸任务集合。

nR表示右侧拆卸任务集合。

li表示拆卸任务i分配至左侧拆卸序列第l个。

ri表示拆卸任务i分配至右侧拆卸序列第r个。

em表示机器人待机能耗。

ed表示机器人二次处理零件时能耗。

Aij表示任务优先关系,若任务j是任务i的紧前拆卸任务,则Aij=1,否则Aij=0。

k(i)为任务位置属性,若为左侧作业则k(i)=1,若为右侧作业,则k(i)=2,若两侧都可则k(i)=0。

目标函数:

F=min[f1,f2,f3,f4];

(1)

(2)

(3)

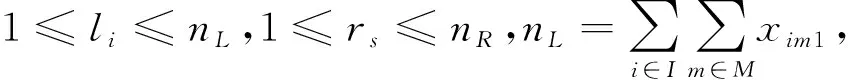
(4)

f4=Edisi+EWS+Ed,

(5)

s.t.

(6)

(7)

Wm-1≥Wm,∀m∈{2,3,…,|M|};

(8)

(9)

(10)

BTimk≥FTjmk+tj,∀i,j∈{i,j|Aij=1};

(11)

(12)

(13)

(14)

对于目标函数:式(1)为最小化目标F,包含4个子目标;式(2)为开启工作站数f1,f1以减少拆卸线作业长度,从而有效减少能耗,提高空间利用率以及拆卸效率;式(3)为空闲指标f2,减少工作站空闲待机时间,均匀分配拆卸任务使工作站负载均衡,减少拆卸资源浪费;式(4)为危害指标f3,将有危害的零件集中尽早拆卸,以此降低拆卸成本;式(5)为多机器人能耗指标f4,包含3种能耗:机器人拆卸任务时拆卸能耗Edisi、机器人在没有拆卸任务时处于待机状态时能耗Ews,以及危害零件、需求零件机器人拆卸完成后对零件二次处理的能耗Es。

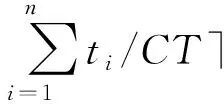
2 改进樽海鞘群算法

2.1 樽海鞘群算法

樽海鞘群算法是受一种深海微生物樽海鞘的捕食行为启发的算法。樽海鞘在海洋中会存在一种聚集行为,它们组成樽海鞘群,然后进行捕食行为和移动行为。樽海鞘群由两类樽海鞘组成:领导者和追随者。领导者是群头部的樽海鞘,其他为追随者。在樽海鞘群算法中,其他的樽海鞘根据最佳领导者位置来更新自己的位置。领导者是矩阵中的第一个向量,它的下一步位置会在一定程度的朝着食物前进。领导者的位置更新公式为:

(15)

(16)

跟随者樽海鞘跟随领导者运动,第i只跟随者下一次迭代位置由当前迭代中它自己的位置以及第i-1只樽海鞘位置共同决定。由牛顿运动定理公式化简得到跟随者位置更新公式:

(17)

2.2 改进的樽海鞘群算法

SSA算法复杂度低且基本不需要参数设置,最大程度上减少了主观因素导致的局部最优解,但是在SSA种群更新过程中会出现种群进化多样性不足导致的局部最优问题。为解决此问题,加入了莱维飞行[19]操作,该操作是模拟自然界中布谷鸟的飞行行为的一种间歇性无规则的全局搜索模式,可以有效跳出局部最优解,提高解的多样性。

2.2.1 莱维飞行操作

莱维飞行操作由式(18)和式(19)来确定移动的步长和领导者位置。因为拆卸线平衡问题属于离散问题,一般选择离散编码方式,所以式(19)失效。结合樽海鞘群算法,将领导者位置的更新步长定义为对应替换任务的位置。任务加权值与随机步长λ结合,最终莱维飞行操作算法具体步骤如下:

步骤1随机选择起点任务i,确定任务在拆卸序列X的位置pi。

步骤2根据优先关系矩阵得到莱维飞行可行解。

步骤3根据式(18)计算莱维飞行随机步长λ。

步骤4确定可行任务集合V。

步骤5由随机步长λ与可行任务集合中最小加权值乘积计算得到加权值阈值w′。

步骤6根据式(19)选择莱维飞行操作的替换任务,更新第t代第j维领导者位置。

步骤7重复步骤2～步骤6,直到完成第t代的第n维操作,第t代领导者位置更新为第(t+1)代领导者位置,莱维飞行结束。

(18)

(19)

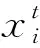
(20)

2.2.2 领导者位置更新操作

领导者位置更新式(16)在离散化问题中无效,可重新定义部分参数解决拆卸线平衡问题。定义maxj为变异操作中可行任务集合中任务位置的上界,minj为可行任务集合中任务位置的下界,由于樽海鞘移动速度较慢,在领导者带领樽海鞘群移动时食物有一定概率被其他海洋浮游生物夺取,设领导者成功获得食物的概率时Pa,通过随机概率Pj～U(0,1)模拟领导者获得食物位置第j维任务i的Pa。具体领导者位置更新操作如伪代码所示:

输入:拆卸序列X,优先关系矩阵A,成功获得食物的概率Pa,种群规模T_size,最大迭代次数Tmax,当前迭代次数t

1 for i=1 to T_size

2 生成[0,1]随机数c2、c3

4 产生随机概率Pi

5 if Pi>Pathen

6 Fij处任务i的紧前任务在拆卸序列中最大位置

7 Fij处任务i的紧后任务在拆卸序列中最小位置

8 生成可行任务V1集合中任务位置的上界maxj

9 生成可行任务V1集合中任务位置的下界minj

10 通过式(16)计算任务i插入位置,产生新解X′

11 将X′保存到解集

12 end if

13 end for

输出:添加新解后的解集

2.2.3 跟随者位置更新操作

跟随者位置更新通过交叉操作实现。以经过莱维飞行和领导者位置更新得到的外部非劣解作为父代1,第一次Pareto之后外部非劣解集中单目标最优解作为父代2,随机选择两个不同的交叉位置,父代1交叉位置区间的任务集合映射到父代2中相应的位置,得到新解。具体位置更新操作如图3所示。

2.3 编码

根据DLBP的特征,本文采用基于任务的编码方式,编码中每一个编号对应一个拆卸任务,每个解对应一个可行的拆卸序列。在编码过程中引入优先关系矩阵Y,如图4所示。Y由0和1组成,其中没有紧前任务的拆卸任务在对应的优先关系矩阵中列元素全部为0,有紧前任务的拆卸任务在矩阵中所对应紧前任务位置处元素为1。随机选择无紧前任务的拆卸任务进行分配,当任务分配至工作站后,将该任务所在列的全部元素改变成1,用它来表示该任务已分配至工作站;将该任务所在行的元素全部变为0,解除该任务对其他为拆卸任务的紧前约束。具体操作方式如伪代码所示:

输入:优先关系矩阵A,种群规模T_size

1 生成一行T_size列空矩阵B

2 fori=1:T_size

3 找到没有紧前任务的所有任务

4 随机选择其中某一个任务放置在空矩阵B的第i个位置

5 将该任务所在列的全部元素改变成1

6 将该任务所在行的元素全部变为0

13 end for

输出:可行任务序列B

2.4 解码

双边拆卸线与单边拆卸线不同,任务具有方位属性且需要分配至两侧工作站,考虑拆卸任务的工位约束。对于有方位属性的任务,结合属性将任务分配至左侧或右侧工作站,对于两边皆可的拆卸任务,建立如下规则来分配任务:若任务既可以分配到左侧又可以分配到右侧,在满足优先关系约束、站内关系约束的前提下,将任务分配至工作站数量少的一侧工作站;若两侧工作站数量相同,将任务分配至空闲时间多的一侧工作站;若同一组合工作站左右两侧剩余可拆卸时间相同,则随机分配至某一侧工作站。当组合工作站内任务填满,即左右两侧工作站数量发生变化时,需要中断任务分配,在开启第二个组合工作站之前进行检查,第一个组合工作站中是否存在既有危害又有需求属性的任务或者是否存在只有危害属性的任务。若第一个工作站中存在带有属性任务,则需要重新选用合适的机器人进行拆卸任务,此时由于机器人型号发生变化,导致分配至第一个工作站的所有任务的任务时间发生变化,这是因为不同型号机器人拆卸同一任务时拆卸时间不同导致的。在再次填满工作站后,需检查此时工作站内任务拆卸时间变化后是否加入额外的有属性任务。规定危害需求任务优先级大于危害任务大于普通任务,即若组合工作站内有危害需求任务,则工作站为危害需求工作站,选用Ⅲ型机器人拆卸,重新分配任务至组合工作站;若组合工作站内有危害任务,选用Ⅱ型机器人拆卸,重新分配任务至组合工作站,在再次填满工作站后,如果站内新加入了危害需求任务,则选用Ⅲ型号机器人拆卸而不是Ⅱ型,重新分配任务至组合工作站;若组合工作站内只有危害任务及普通任务,选用Ⅱ型机器人;若组合工作站内没有带有属性的任务,则选用Ⅰ型机器人拆卸,不需要重新分配任务。具体解码流程图如图5。

2.5 种群更新策略

在群智能算法中,种群更新策略的不同会影响算法的收敛性和分布性。在ISSA算法中,在每次迭代后外部储存非劣解,运用精英策略将外部档案中的非劣解随机插入下一代初始种群中,以提高下一代初始种群的质量,从而加速算法寻优过程。

2.5.1 外部档案更新机制

本文所提ISSA算法求解大规模算例时所产生偏差向量的维度较大,变异交叉后得到的较优个体较多,若将非劣解放入外部档案,使其规模急剧增大,则算法运算效率大幅度降低。因此,本文采用Pareto解集处理多目标问题。任意两个解X1、X2满足式(20),则表明X1的目标值F(X1)优于X2的目标值F(X2),称X1支配X2。Pareto最优解集包含的非劣解不可被可行决策空间任意解支配,其所对应目标值的集合称为Pareto最优前沿。

(20)

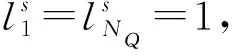
(21)

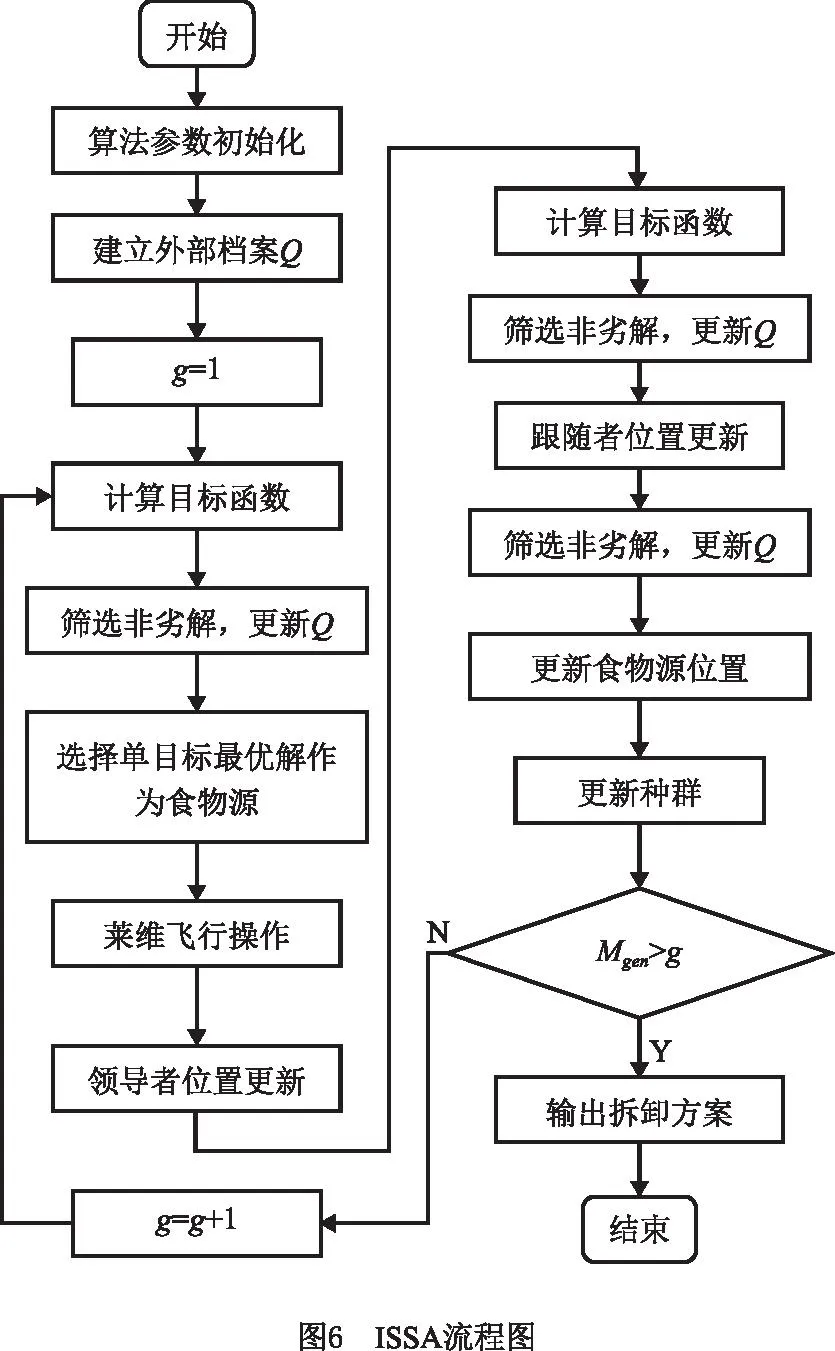
2.6 ISSA算法流程

本算法求解双边多机器人拆卸线平衡问题的流程图如图6。

3 算例验证

为验证所提ISSA算法的可行性与优越性,引用单边拆卸线经典案例以及已有文献中双边实例的求解结果与本文所提算法对比。为保证算法的公正性,对比所用结果皆引用于已发表文献。本文所提算法测试实验所使用的计算机配置为Intel(R)Core i5-6300HQ @ 2.30 GHz四核,8 GB内存,在win10系统下MATLAB R2019b运行。

3.1 大规模算例验证

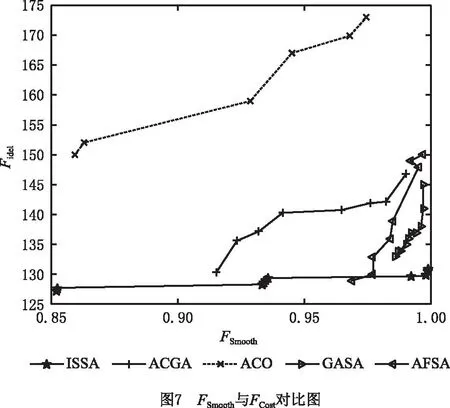
应用文献[26]中52拆卸任务的大规模案例。该案例的目标函数为闲置率Fidel,负载均衡指标Fsmooth以及拆卸成本Fcost作为目标函数求解。已有求解该算例的算法有:蚁群遗传优化算法(Ant Colony and Genetic Algorithm,ACGA)[25]、蚁群算法(Ant Colony Optimization,ACO)[26]、混合遗传模拟退火算法(Genetic Algorithm and Simulated Annealing,GASA)算法、人工鱼群算法(Artificial Fish Swarm Algorithm,AFSA)[27]。综合考虑算例特点与算法结构,通过在不同参数值下大量计算,选取结果相对较优参数作为大规模算例参数。设定参数如下:种群规模N=200,最大迭代次数G=300,捕食率Pa=0.4,外部最优种群Q=10。独立运行10次,随机选取一次求解结果,各目标最优值用粗体表示,如表1所示。将求解结果与以上算法求解结果做对比,由于闲置率计算结果均为0.057 9,建立二维直角坐标轴,将负载均衡指标与拆卸成本两个目标函数进行比较,结果如图7所示。

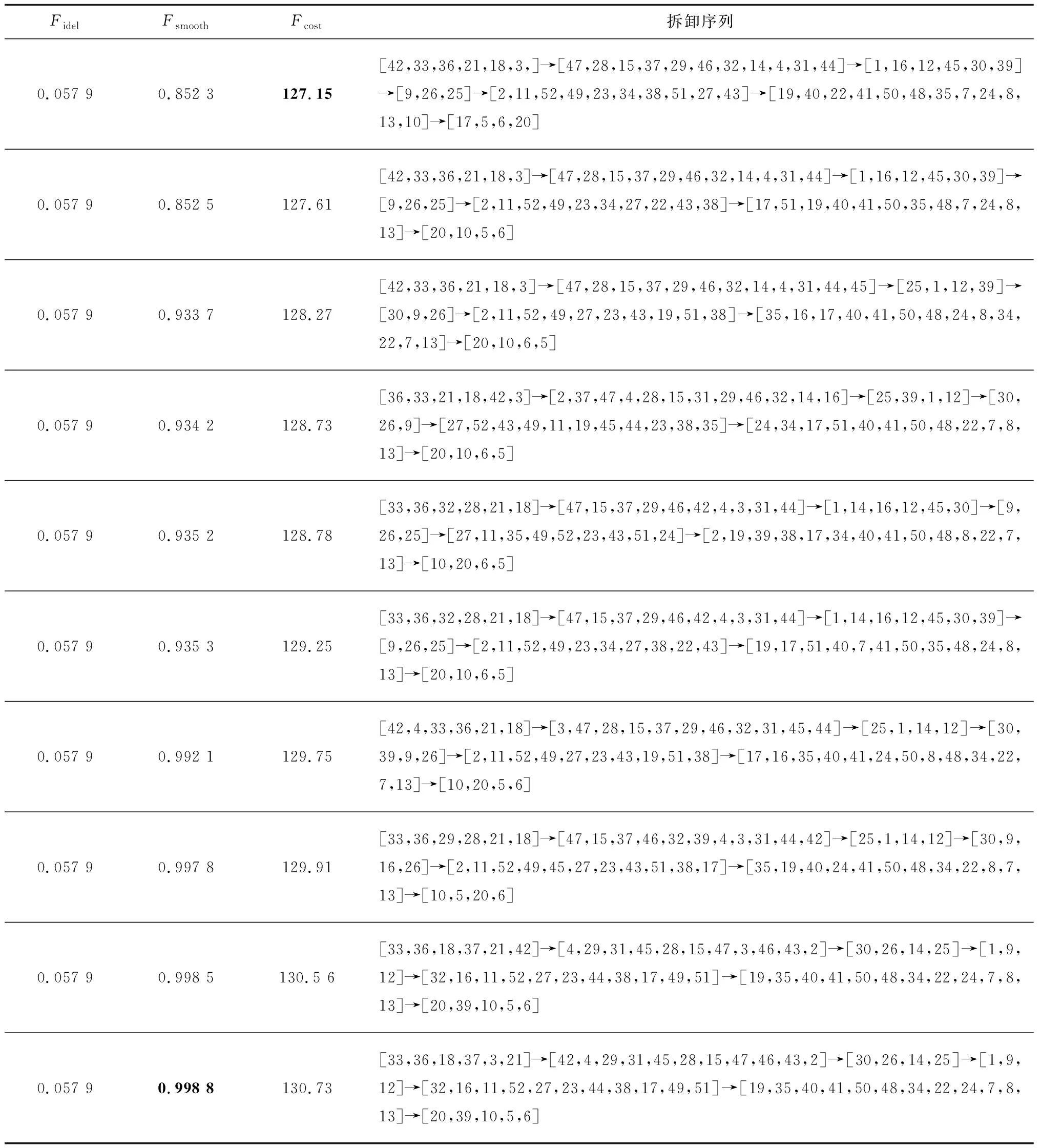
表1 ISSA对P52问题求解结果

由表1可知,算法平滑率在0.852 3～0.998 8之间,拆卸成本在127.15～130.73之间,所提算法求解方案中,负载均衡指标Fsmooth最大值为0.998 8,拆卸成本Fcost最小值为127.15,所求结果均优于以上所列算法Fcost最优值。由图7可知,ISSA算法结果在每一项目标值均占优,包围其余4种算法的解,验证了该算法在运用在大规模案例求解时的可行性与有效性。

3.2 双边实例验证

应用文献[8]电冰箱的拆卸实例,该实例目标函数分别为:工作站指标(F1),需求指标(F2)、空闲指标(F3)、危害指标(F4)。用本文所提ISSA算法求解该案例所设置参数:种群规模N=200,最大循环次数G=200,捕食率Pa=0.3,外部最优种群Q=10。算法独立运行10次,取其中较好的一次与文献中所用BA算法进行对比,求解结果如表2所示,表中可见该文献中所用的蝙蝠算法所求的工作站指标F1范围为6～9,空闲指标F3范围为5 907～51 679,需求指标F2范围为435～461。本文算求得工作站数目在5～8之间。当工作站指标F1为5时,ISSA算法所求得空闲指标F3及危害指标F4为755和29,远小于BA算法。当两种算法求得工作站指标F1都为8时,对比F2、F3和F4得出ISSA算法求得的解完全占优BA算法。综上所述,ISSA算法在求解双边问题性能上优于BA算法。

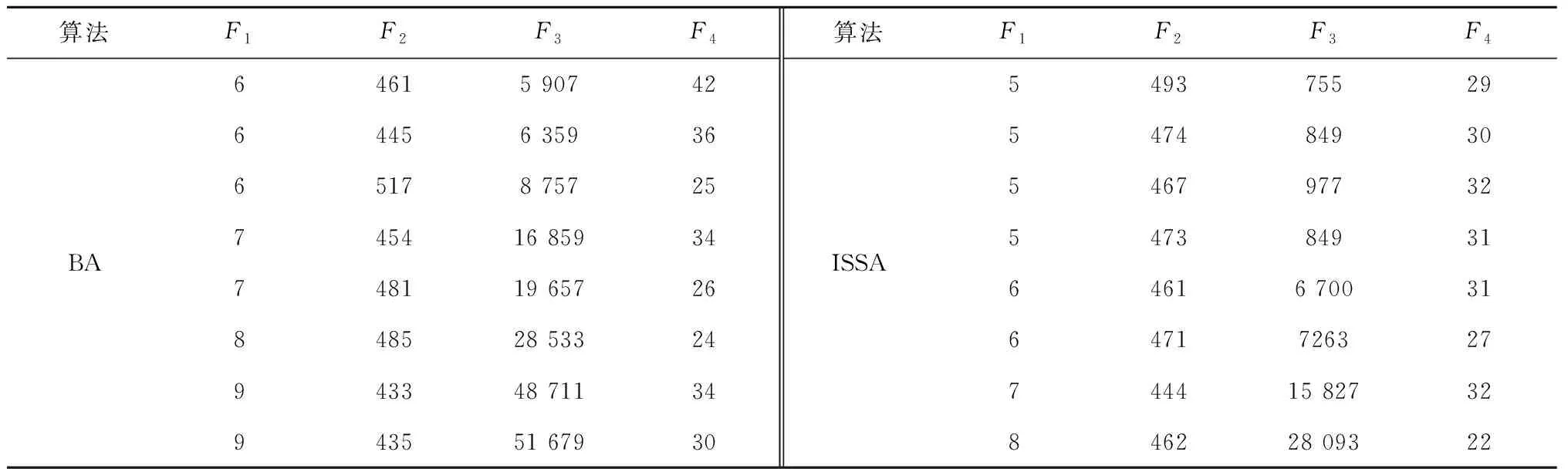
表2 BA与ISSA对电冰箱P25问题求解结果

3.3 实例应用

为了增加本研究实用性,选用某公司废旧汽车完全拆卸实例。该汽车由40个拆卸任务组成,每项拆卸任务拆卸时间(单位:s)取3次拆卸时间平均值。需求数量(单位:个)由目前市场需求调查统计得出。任务拆卸方向由工厂中所分配的拆卸方向决定,1表示左侧拆卸,2表示右侧拆卸,0表示两侧均可进行拆卸。机器人能耗(单位:kW)信息如表3所示,其中效率表示拆卸某任务所需时间的倍数。总拆卸任务信息表如表4所示,任务优先关系图如图8所示。

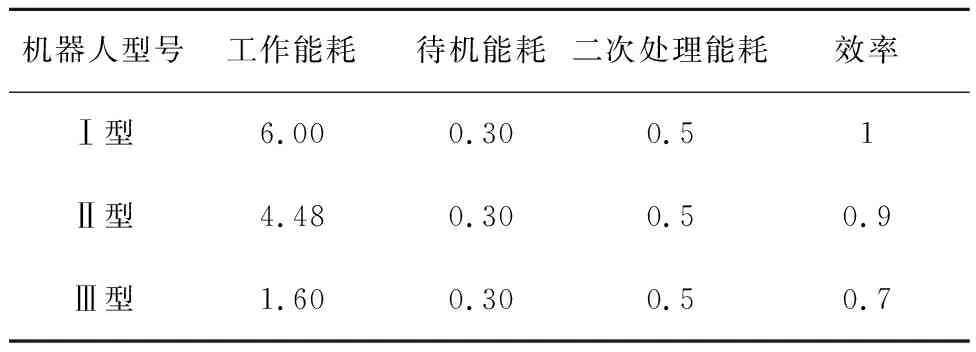
表3 机器人信息表

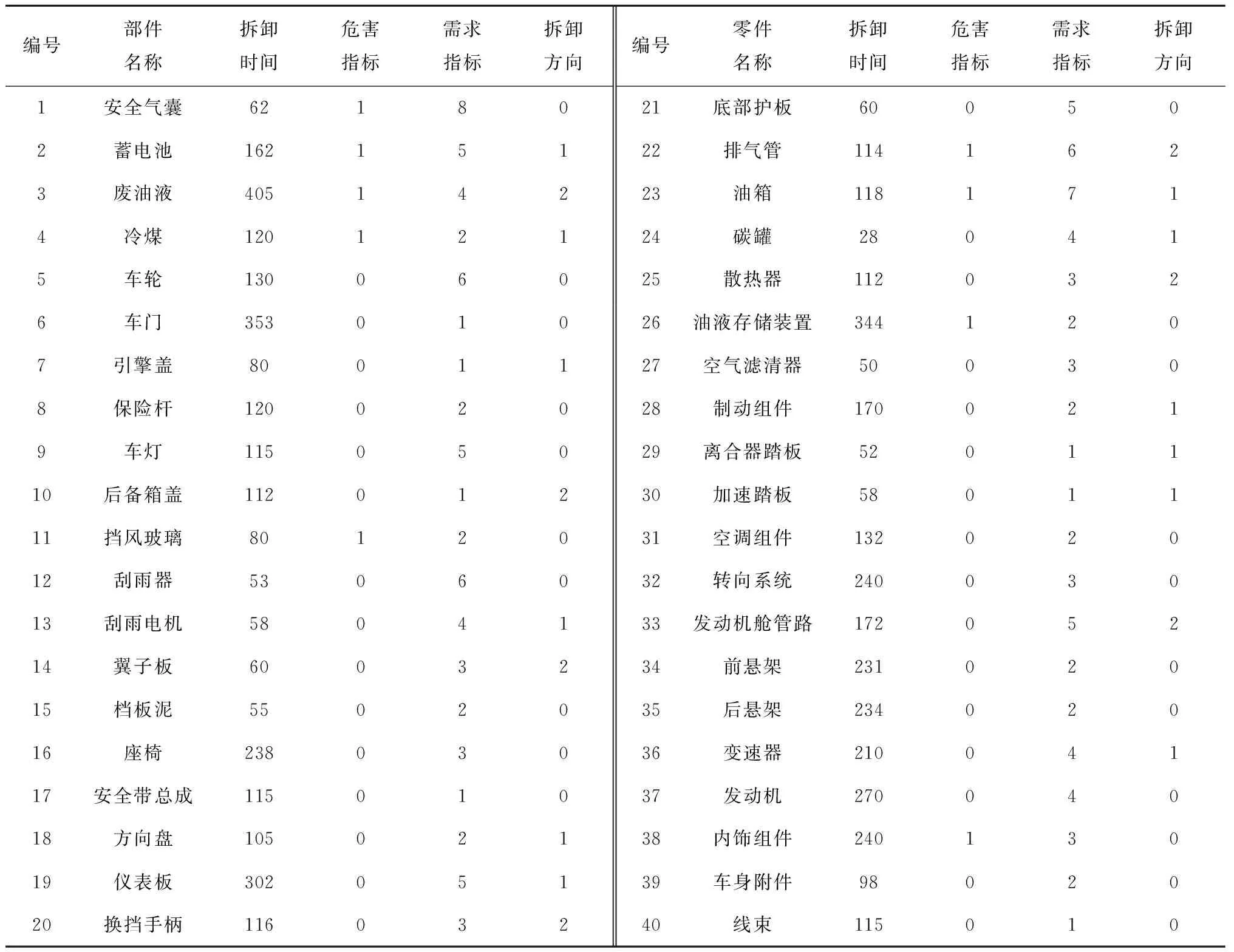
表4 拆卸任务名称表

由大量实验测试,设定算法参数如下:种群规模N=200,迭代次数G=300,捕食率Pa=0.3,外部最优种群Q=12。算法独立运行10次,随机选择一次结果,如表5所示。

表5 ISSA对P40汽车拆卸求解结果

由表5可以看出,所提ISSA算法求得的12组方案中,方案1～方案10最小化工作站数均为9,方案2～方案4最小化空闲时间为116117,方案1最小化危害指标为59,方案12最小化机器人能耗为15051240。企业若是重点考虑空闲时间和工作站个数,可选择方案2、3、4;若只考虑机器人能耗指标,可选择方案11;若考虑危害指标,可选择方案1;若综合考虑,可选择方案5。方案5中4项指标均较优秀,其中最小工作站数为9,达到最小值。方案5和方案11甘特图如图9～图10所示,其中蓝色为Ⅰ型机器人,橙色为Ⅱ型机器人,蓝白色为Ⅲ型机器人。

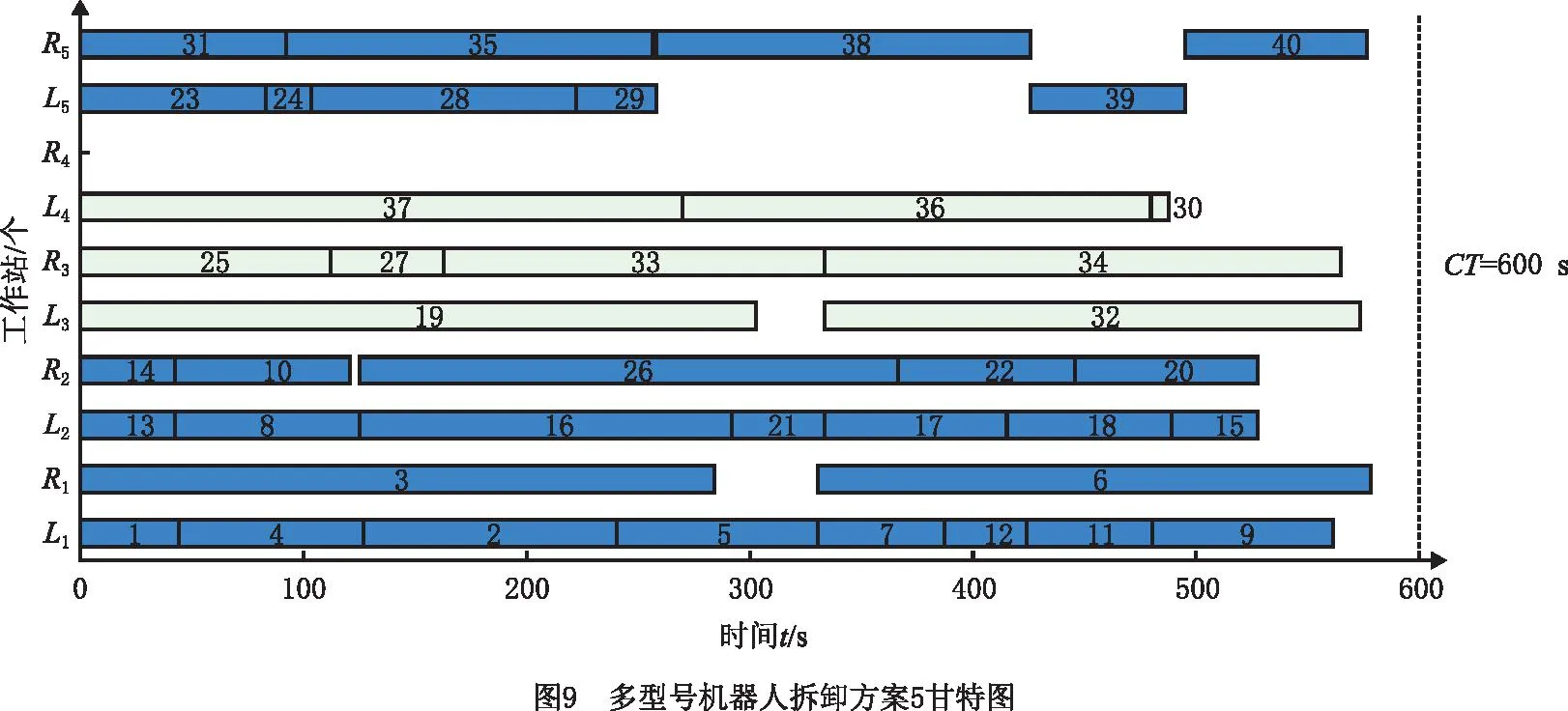
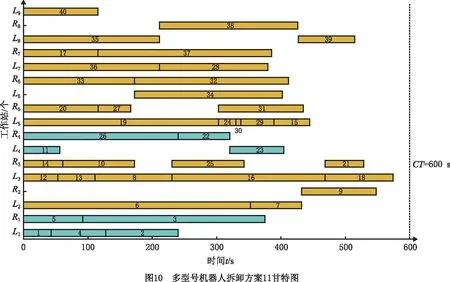
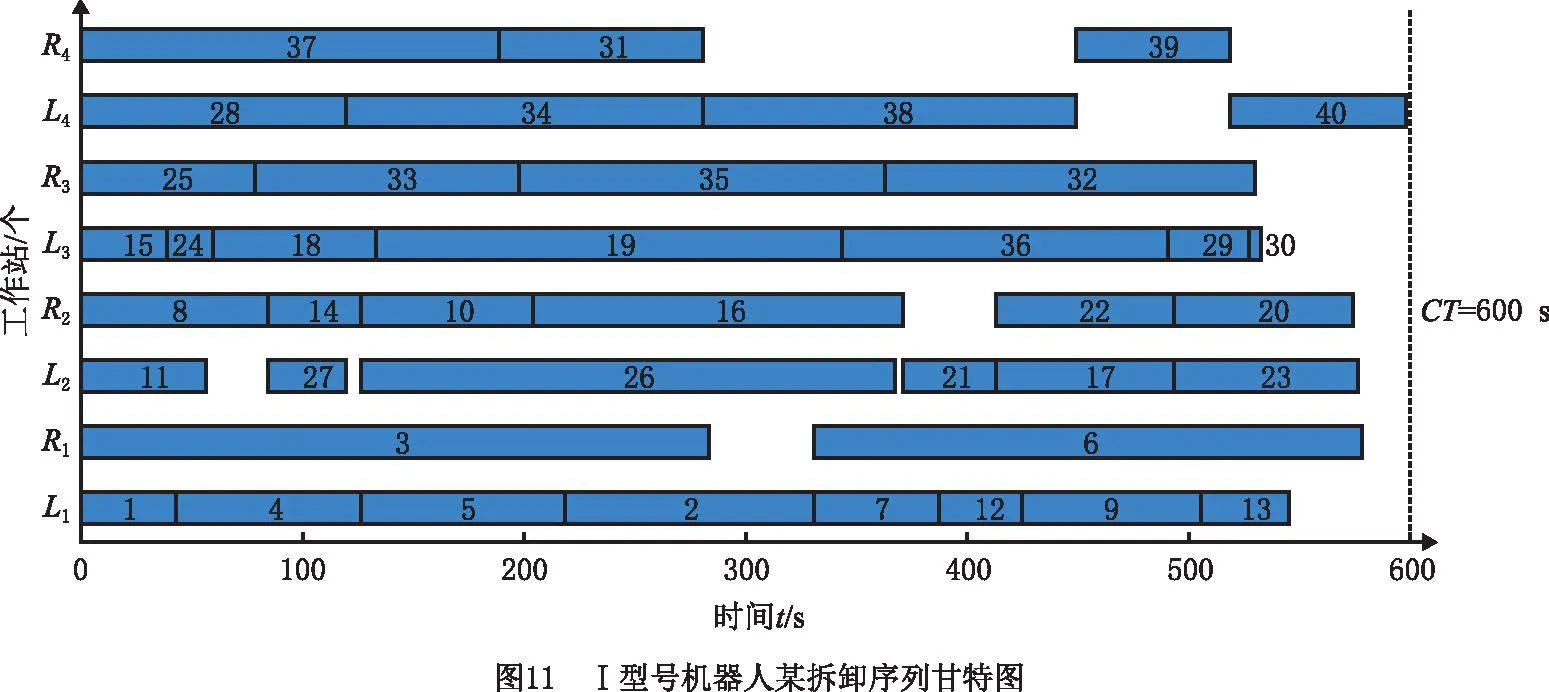
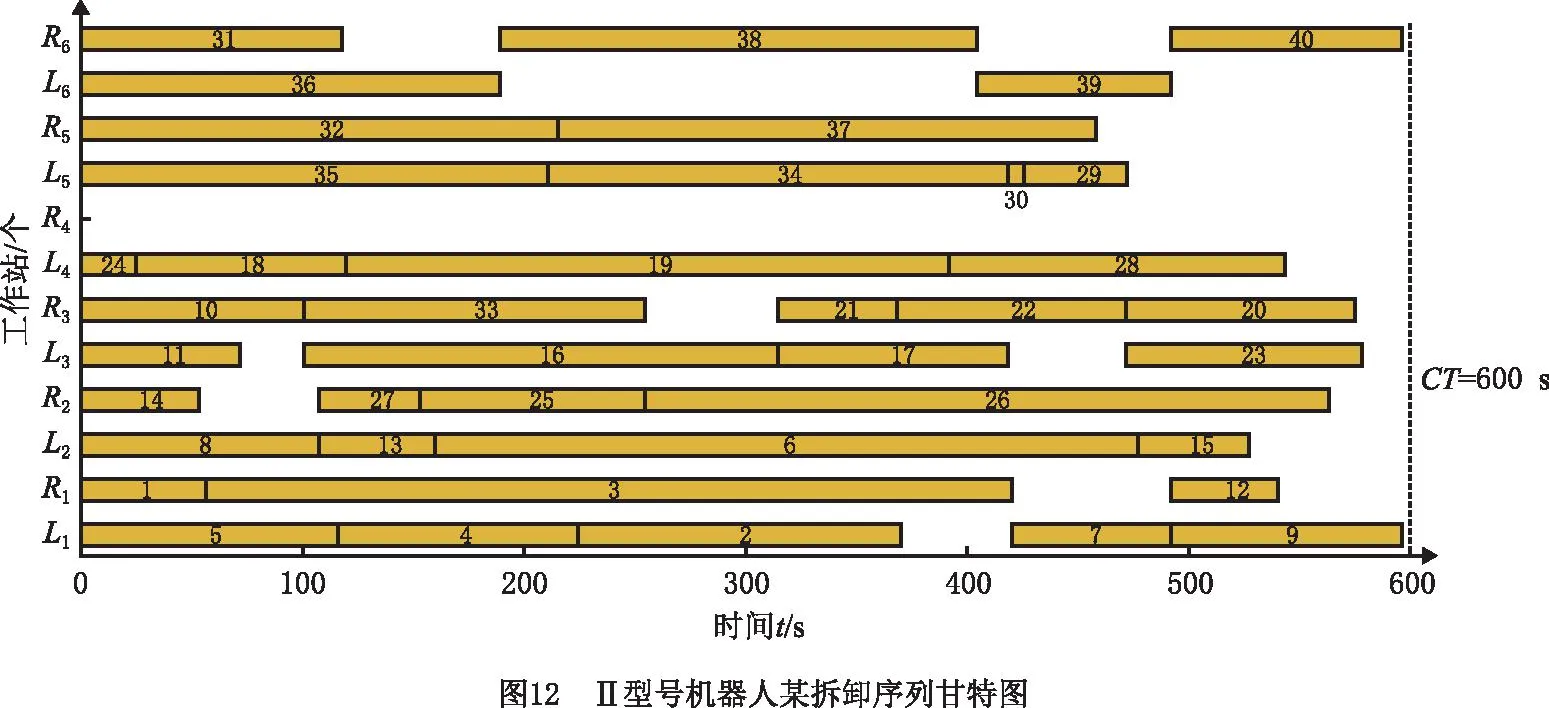
为与本文多机器人问题求解结果进行对比,以P40废旧汽车拆卸为实例,采用单一型号机器人拆卸,求解结果分别如表6所示。随机取一方案做甘特图,如图11～图13所示。在全部采用Ⅰ型机器人的情况下,方案减少了线长,最小化工作站数为8,但能耗均大于多机器人拆卸方案;若全部采用Ⅱ型机器人,最小化工作站数为11,方案10能耗最低,为30 324 500,但工作站数为18,线长大大增加;若全部采用Ⅲ型机器人,最小化工作站数为12,最小空闲时间为226 281,最小危害指标为47,最小能耗为31 943 300。在最小工作站数情况下,Ⅲ型机器人其余三项指标均高于多型号机械人拆卸指标。可以看出,多型号机器人在废旧汽车完全拆卸实例中具有优越性。

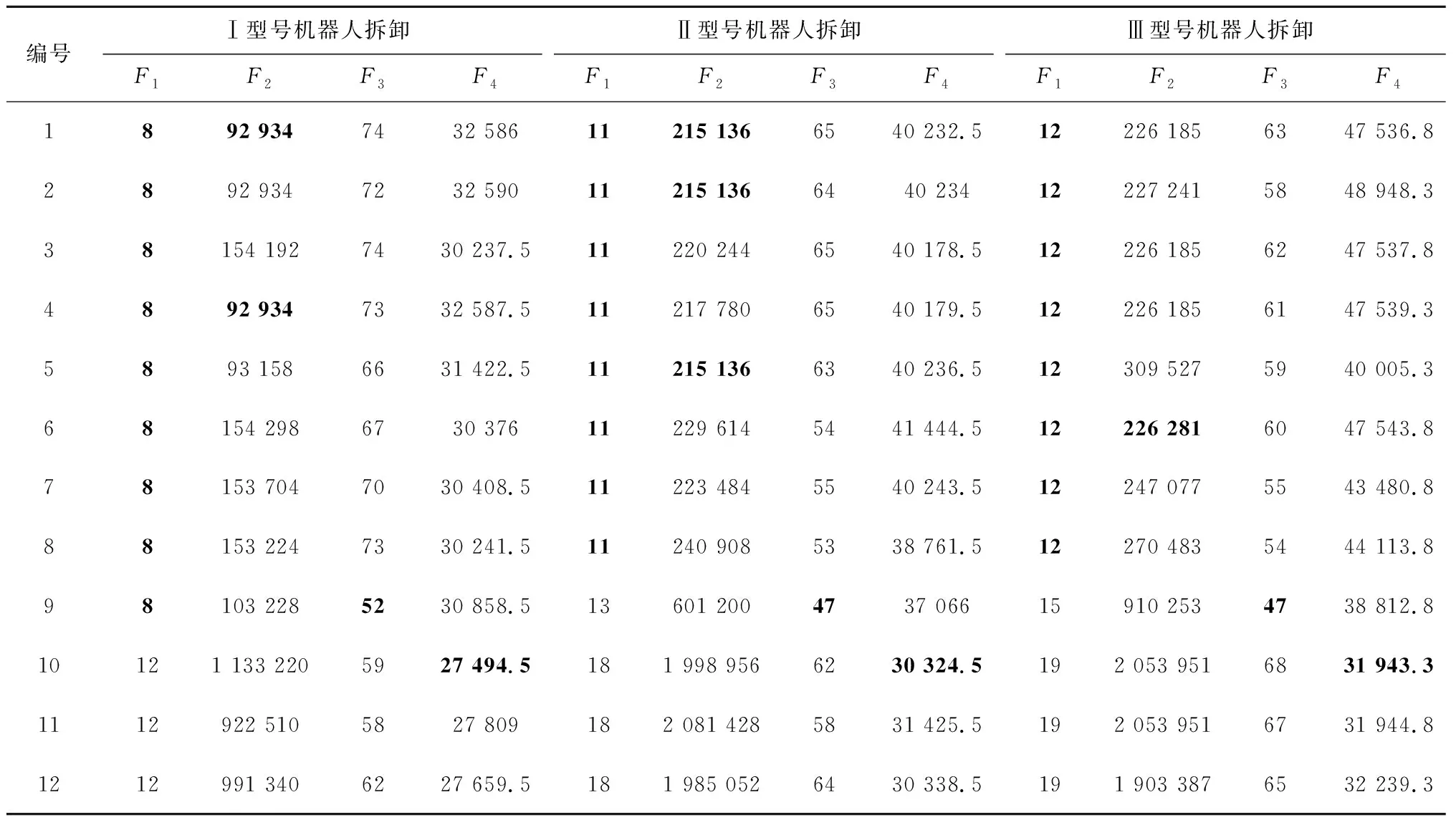
表6 不同型号机器人对P40汽车单独拆卸求解结果

4 结束语

针对现有机器人双边拆卸线中未考虑由于机器人型号引起拆卸时间变化的问题,本文建立了改变任务时间的多型号机器人双边拆卸线数学模型,提出了一种改进的ISSA算法求解以最小化工作站数、负载均衡指标、危害指标和机器人能耗为优化指标的多目标拆卸线平衡问题。本文主要贡献如下:

(1)首次考虑了多型号机器人在双边拆卸线平衡问题中的应用,并创新性的对机器人型号进行了划分,使问题更加贴近实际。对所建模型进行了系统的阐述,分析了机器人由于型号不同引起的能耗问题。针对机器人由于型号问题造成拆卸任务时间的不同的问题,首次在双边拆卸线解码中加入了对应的任务重分配规则,保证了求解结果的合理性和高效性。

(2)将莱维飞行策略融入到樽海鞘群算法中,减少了种群进化多样信号不足导致局部最优的问题,加强了算法的寻优能力和全局搜索能力。结合Pareto思想及拥挤距离机制,保证了解的多样性与优越性。应用所设计算法分别求解了P25和P52拆卸线经典案例,并对比了有关智能算法,验证了所提算法在解决普通问题时具有有效性和优越性。为保证算法在解决双边拆卸问题时具有同样的优越性,将算法应用于电冰箱P25拆卸实例,并与相关算法进行了对比,保证了算法的优越性。最后,计算某废旧机车拆卸实例,求解得到12种高质量解,决策者进行选择。

在未来研究中,对于双边拆卸线中机器人拆卸不同零件时更换末断执行工具的情况可以进行思考,从机器人类型与任务的匹配性研究出发,并考虑同站内机器人干涉问题。因此,考虑干涉、多适配机器人双边拆卸线平衡问题值得进一步研究。