基于KD树和混沌蜉蝣优化的并行谱聚类算法
2024-01-13刘祥敏毛伊敏陈志刚
胡 健,刘祥敏,毛伊敏+,陈志刚
(1.江西理工大学 信息工程学院,江西 赣州 341000;2.赣南科技学院 信息工程学院,江西 赣州 341000;3.中南大学 计算机学院,湖南 长沙 410000)
1 问题的提出
聚类分析[1]作为一种无监督学习,在数据挖掘和机器学习领域中扮演着至关重要的角色,它根据数据对象的特征对数据集进行聚类,使类内相似度最大化、类间相似性最小化,从而发现对象间的内在联系,获取蕴藏在数据背后的价值。然而,随着大数据时代的来临,爆炸式增长的数据使得传统聚类算法的计算性能瓶颈愈加突出,这严重制约了聚类算法在大数据集上的应用。因此,如何降低大数据环境下聚类算法的计算开销成为了一个具有挑战性的问题。
近年来,随着MapReduce并行计算模型以及Hadoop、Spark[2-4]等大数据分布式并行计算框架的快速发展,聚类算法的并行化研究逐渐得到了广泛的关注,相关研究如表1所示。SREEDHAR等[5]设计了基于MapReduce框架的并行k-means算法KM-I2C,根据聚类间和聚类内相似性将不同聚类划分为子聚类,一定程度上提高了聚类精度,但未能合理地调度map和reduce作业从而容易出现节点负载不均衡。针对此问题,文献[6]引入池塘采样方法以等概率采样输出中间数据,然后采用第一自适应调度,将中间数据合理地放入节点,有效地解决了负载不均衡的问题。但该算法对质心的初始化可能存在局部最优问题。为此,文献[7]先初始化随机抽样,然后并行化距离计算过程,最后并行执行聚类分析,该算法处理大规模数据时具有良好的收敛性和较高的聚类精度,但在处理高维数据时仍然存在问题,且聚类精度有待提升。此外,胡健等[8]提出了基于MapReduce和加权网格信息熵的DBWGIE-MR算法,通过构建加权网格加强网格间的关联性,从而提高聚类精度;ATILAGN等[9]提出了FN-DBSCAN算法,该算法首先计算成对距离,然后计算模糊邻域,并通过向队列中添加核心点的邻居来迭代得到局部簇,最后合并得到最终聚类结果,这些过程都是并行的,在保证聚类精度的同时减少了运行时间。尽管以上算法都取得了不错的效果,但在处理高维数据时均易陷入“维数灾难”,从而导致巨大的计算开销。

表1 相关算法比较分析
谱聚类算法[10-11]作为一类新颖的聚类算法,能够对高维、任意形状的样本空间进行聚类,已被证明在非凸样本空间中比传统的聚类算法(如k-means)更加有效[12],并在图像分割[13-15]、推荐系统[16]、社区发现[17]、计算机视觉[18-20]等领域得到了广泛的应用。由于谱聚类算法的诸多优点,一些学者开始研究谱聚类算法的并行化。CHEN等[21]比较了传统的相似矩阵稀疏化方法与Nystrom近似方法,提出了并行潽聚类(Parallel Spectral Clustering,PSC)算法,该算法首先基于MapReduce构造稀疏相似度矩阵,将数据实例分发到分布式节点上,在每个节点上使用最小磁盘I/O的方式计算本地数据和整个集合之间的相似性;然后将特征向量矩阵存储在分布式节点上,并行求解特征向量矩阵和k-means聚类。PSC算法实现了谱聚类在分布式系统上的并行化,在大数据集上实现了良好的加速。文献[22]将MapReduce与谱聚类算法结合,实现了并行谱聚类算法(Parallel Spectral Clustering Algorithm, PSCA),该算法在节点分配数据时,将索引i和索引n-i+1的数据点放在一起计算相似值,在建立稀疏相似矩阵时可以保证每对数据点之间的相似值只计算一次;在计算特征向量时,将Laplacian矩阵存储在Hadoop文件系统中,通过分布式Lanzos操作得到特征向量;最后利用并行k-means聚类处理特征向量的转置矩阵,得到聚类结果。在此研究基础上,文献[23]在实现t近邻稀疏化相似度矩阵时引入KD树(k-dimension tree)索引技术,加快搜索近邻范围,并通过实验证明提升了算法性能。但是,以上算法存在4个问题:①分配数据时,不管是采用MapReduce的默认分区策略还是将索引i和索引n-i+1的数据放在一起,对数据的分配具有随机性,未能根据数据的分布特性采用合理的数据划分方法,节点执行任务时容易产生负载不均衡的问题;②在构建稀疏矩阵过程中,尽管用KD树索引技术在一定程度上可以减少计算,但是KD树只适用于低维数据,在高维数据上可能需要大量的时间来回溯树和最优解,依然会产生大量的冗余计算从而导致搜索性能下降;③在正规化Laplacian矩阵时,在各节点上分布式计算矩阵相乘操作,时间开销大;④用k-means算法进行最终聚类时,仅是简单地并行化,没有解决随机选取初始聚类中心引起的初始中心敏感问题,从而可能导致聚类效果不够稳定。
针对以上问题,本文提出基于KD树和混沌蜉蝣优化算法的并行谱聚类算法(Parallel Spectral Clustering algorithm using KD-tree and chaotic Mayfly Optimization algorithm, PSC-MO),主要工作可归纳为以下4点:
(1)提出了基于采样的KD-tree数据分区策略(Data Partitioning Strategy, DPS)划分数据以获得均匀的分区,实现了各节点的负载均衡;
(2)采用KD树索引实现t近邻稀疏化,提出了优化的分区分配策略(Optimized Partition Assignments strategy, OPA)和基于三角不等式的KD树剪枝策略以进行跨分区的t近邻搜索,避免了冗余计算,从而提高了搜索效率;
(3)实现了Laplacian矩阵构建与正规化过程的并行化,并提出正规化定理,通过元素对应相乘的方式代替矩阵相乘以优化Laplacian矩阵正规化过程,进一步减少了时间开销;
(4)设计了混沌蜉蝣优化算法(Chaotic Mayfly Optimization Algorithm, CMO),用于获取最佳的初始簇中心位置,有效解决了算法对初始簇中心敏感的问题。
2 相关算法及概念介绍
2.1 KD树
KD树是一种对k维空间数据进行组织和存储的树形数据结构,用垂直于坐标轴的超平面把一个k维空间划分成多个不相交的k维超矩形区域,由BENTLEY等[24]于1975年首次提出。传统的KD树常用于近邻搜索中,在低维数据上非常有效,但在高维数据上表现差强人意。于是,研究人员发展了许多KD树的变体,如PCA(principal component analysis)树[25]、RP(random projection)树[26]和三进制投影树[27]。此外,PROCIPOUC等[28]提出Bkd-tree用于索引大型多维点数据集;ADAMS等[29]设计了一种能用于高维空间的高斯KD树,可支持快速的Monte Carlo采样查询;WU等[30]提出随机投影KD树,将高维数据点投影到低维空间;文献[31]提出一种随机KD树,通过构建多个并行搜索的随机KD树进行近似最近邻搜索。基于RP树搜索精度高的优点,RAM等[32]提出一种新的KD树用于近邻搜索。
2.2 蜉蝣算法
蜉蝣算法(Mayfly Algorithm, MA)是2020年由ZERVOUDAKIS等[33]提出的一种模拟蜉蝣的社会行为的优化算法,该算法结合了群智能算法与进化算法的主要优点,将最优的雄性个体与最优的雌性个体交配得到最优的子代。MA算法主要包括雄性蜉蝣的运动、雌性蜉蝣的运动、蜉蝣交配。
(1)
更新雄性蜉蝣的速度为:
(2)
其中:g为引力系数;a1、a2为正吸引系数;β为能见度系数;rp、rg为蜉蝣当前位置与历史最佳位置和最佳蜉蝣位置的笛卡尔距离;xhi为蜉蝣历史访问过的最佳位置;xg为种群中最佳雄性蜉蝣位置;d为舞蹈系数;r1为[-1,1]均匀分布的随机数。笛卡尔距离计算公式为:
(3)
(2)雌性蜉蝣的运动 假设a3为正吸引系数,β为能见度系数,rmf为雄性与雌性蜉蝣间的笛卡尔距离,fl为随机飞行系数,r2为[-1,1]均匀分布的随机数,更新雌性蜉蝣的速度为:
(4)
(3)蜉蝣交配 根据适应度函数选择蜉蝣进行两两配对,适应度最优的雄性蜉蝣个体和适应度最优的雌性蜉蝣个体交配,适应度次优的雄性蜉蝣个体和适应度次优的雌性蜉蝣个体交配,以此类推,交配得到两个子代,其子代为:
(5)
式中:male表示雄性父代;female表示雌性父代;L∈[-1,1]为高斯分布中的随机数;offspring1和offspring2表示两个子代,子代的初始速度为0。
2.3 混沌
Sin混沌映射是由正弦三角函数派生的正弦映射,其映射折叠次数无限,比Logistic映射具备更佳的混沌特性[34],其映射方程为:
xn+1=S(xn)=μsin(πxn),-1≤xn≤1,
xn≠0,n=0,1,…,N。
(6)
式中:S(xn)表示Sin映射;x为迭代值;μ为控制参数,μ∈[0,1]。
2.4 谱聚类算法
谱聚类算法将聚类问题转化为图的最优切分问题,其本质是通过特征分解将原始的高维数据空间映射到低维特征向量空间,然后在特征向量空间中对数据点进行聚类。NG等[35]提出的经典谱聚类的步骤为:
(1)构建相似度矩阵W、对角矩阵D,
(7)
(2)计算Laplacian矩阵L并正规化:
L=D-W,
(8)
(9)
(3)计算矩阵的前k个最小特征向量,构成特征向量矩阵Z∈Rn×k;
(4)用k-means算法将数据点vi∈Rk(i=1,…,n)聚类。
在文献[35]的基础上,研究人员对谱聚类进行了若干研究。为解决传统谱聚类算法对尺度参数敏感的问题,ZELNIK-MANOR等[36]提出一种自适应的谱聚类方法,根据其邻域信息为每个点计算一个自适应参数。LIU等[37]通过局部密度获取数据中的隐式聚类结构特征,并与自适应的高斯核函数相结合,提出一种基于共享邻域自适应相似度的谱聚类算法;WANG等[38]提出一种基于消息传递的谱聚类算法(Spectral Clustering algorithm based on Message Passing,MPSC),利用密度敏感相似度来度量数据间的相似度。在流式计算场景下,文献[39]提出一种流式数据相似性计算方法。此外,YANG等[40]中提出一种深度谱聚类学习方法,用相对熵将双自编码网络和深度谱聚类融合;文献[41]设计了normalized min cut问题的连续松弛,并通过训练图神经网络来进行谱聚类分析。虽然谱聚类算法具有良好的聚类性能,但是处理大规模数据集时,存储相似度矩阵、求解特征向量存在资源占用瓶颈。为此,一些学者对谱聚类进行了并行化研究[21-23],将数据分发到多个计算节点进行分布式处理。另外,为避免存储稠密的相似度矩阵,学者们提出了许多改进算法,主要有两个改进方向:①稀疏化相似度矩阵,包括设置阈值和t近邻两种,计算后只存储矩阵中的非零元素;②子矩阵方法,即对相似度矩阵的行或列进行采样,只计算部分数据间的相似性,最经典的是FOWLKES等[42]提出的NystrÖm近似算法。
3 PSC-MO算法
PSC-MO算法主要包括4个阶段:数据分区、并行构建相似度矩阵、并行计算特征向量、并行聚类。
(1)在数据分区阶段,提出DPS策略,对原始数据执行KD树分区,获取均匀的数据分区。
(2)在并行构建相似度矩阵阶段,首先计算分区内部数据的t近邻,然后提出OPA策略和两个基于三角不等式的剪枝策略,在此基础上进行跨分区的t近邻搜索,最后计算数据点与其t近邻的相似度值,构建稀疏相似度矩阵。
(3)在并行计算特征向量阶段,提出正规化定理,通过矩阵对应位置元素相乘的方式得到正规化Laplacian矩阵,求解前k个特征向量构成特征向量矩阵并正规化。
(4)在并行聚类阶段,调用混沌蜉蝣优化算法以获取最优的初始簇中心,然后进行k-means聚类,获取最终聚类结果。
3.1 数据分区
目前,并行谱聚类算法划分数据时大都采用MapReduce默认的数据分区器,忽略了数据间的分布特性,容易产生数据倾斜,从而引起节点负载不均衡。针对这一问题,本文提出基于采样的KD-tree数据分区策略(DPS),得到Map上的数据分区。该策略包括5个主要步骤:采样、支撑点选择、映射、空间划分和数据划分。
(1)采样 为降低映射成本,对原始数据集D={v1,v2,v3,…,vn}进行随机采样,得到采样数据集S(如图1a中黑点为采样数据)。
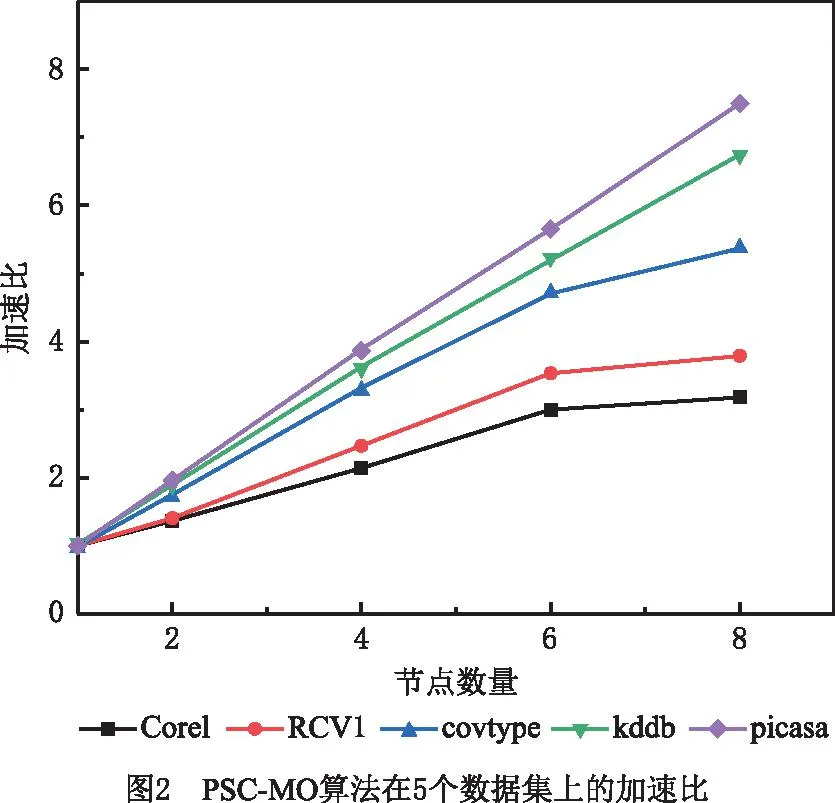
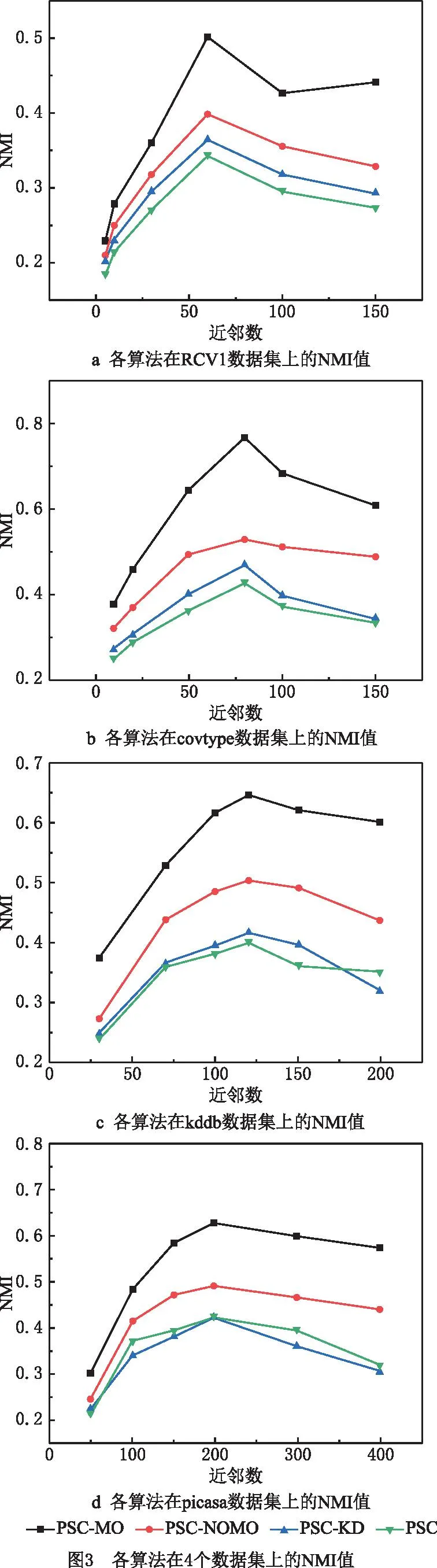
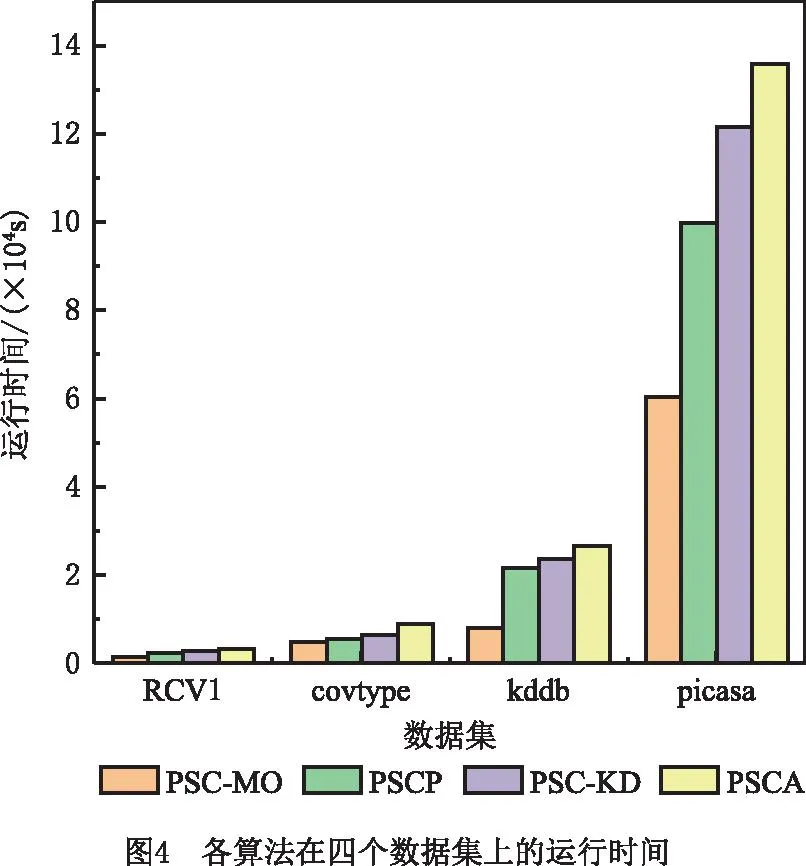
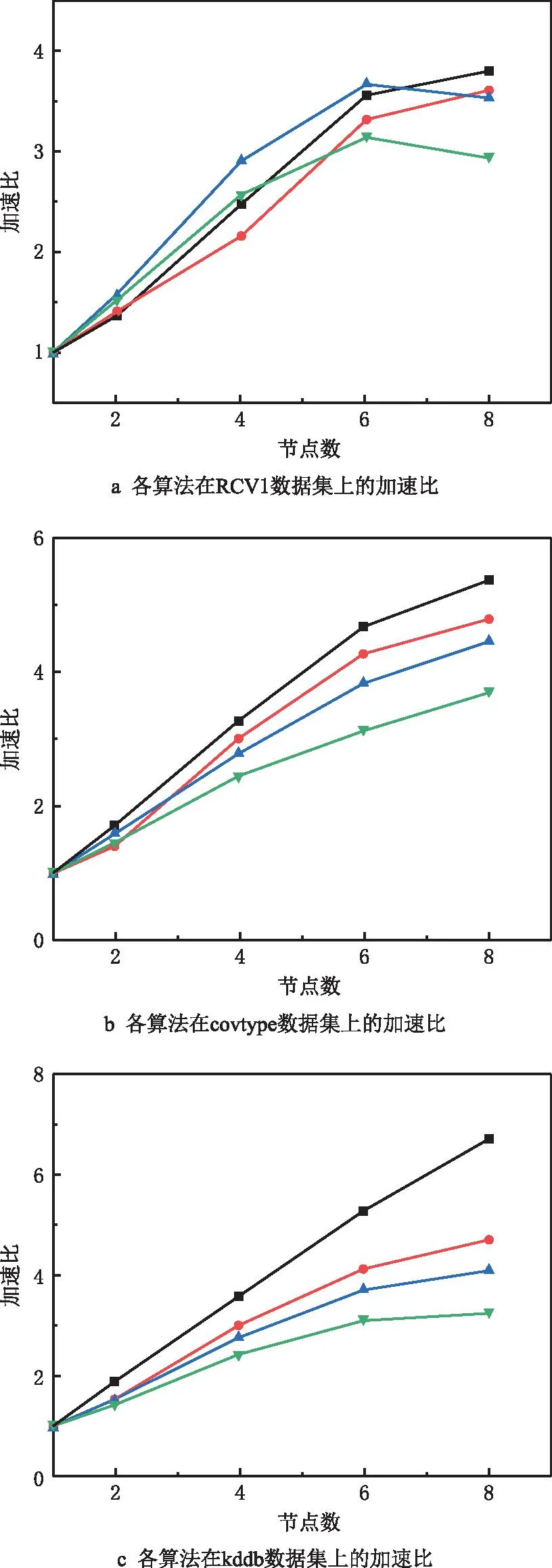
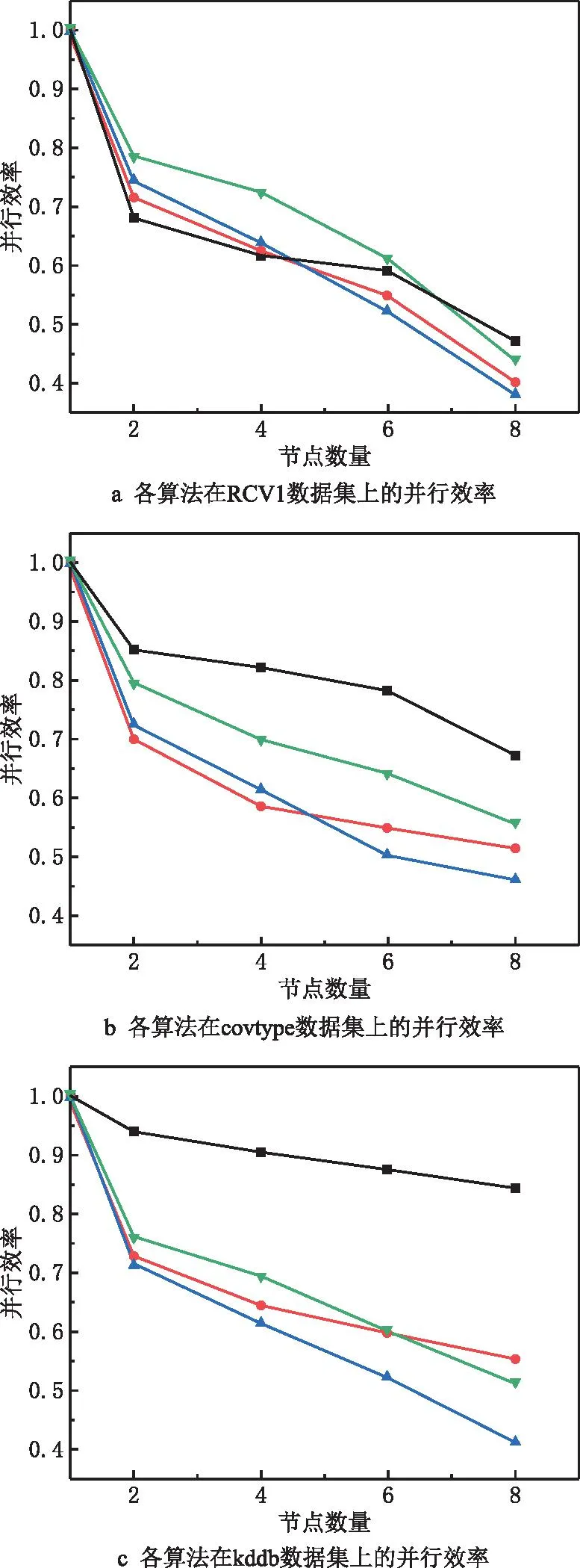
(2)支撑点选择 首先从采样数据集S中随机选出第一个点;接着依次选出后续的支撑点,每次选择到近期被选出的两个点(文献[43]中已证明以近期选出的两个点或三个点为基准时选出的支撑点较为理想)距离最大的点,得到候选集,并从候选集中组合出所有的支撑点集合;最后从S中随机抽取数据构造评价集,将评价集中的数据两两组合成数据对,选出能排除最多数据对的那组支撑点(假设为q个)即为最优的支撑点集合PS={PS1,PS2,…,PSq|q< (3)映射 提出数据映射定理,根据选定的支撑点将数据映射到q维向量空间。如图1a所示,二维空间q=2,PS={PS1,PS2},对任一数据点vi(1≤i≤n),x轴表示vi到PS1的距离d(vi,PS1),y轴表示vi到PS2的距离d(vi,PS2)。 定理1数据映射。给定一个支撑点集合PS={PS1,PS2,…,PSq},若vi、vj是PS构成的度量空间中的点,其中vi、vj∈v且i≠j,则vi、vj可以映射到同一个q维向量空间且保留原始数据间的相似性。 证明根据三角不等式d(vi,vj)≥max{|d(vi,PSu)-d(vj,PSu)||PSu∈PS,u∈[1,q]}=D(φ(vi),φ(vj)),其中D()为无穷范数,φ(vi)、φ(vj)分别表示vi、vj的映射向量,φ(vi)= (4)空间划分 首先选出方差最大的维度,根据数据集S在该维度上的值进行升序排序,选出中位数作为根节点,小于根节点的数据分配给左子树,大于根节点的数据分配给右子树。划分时对于恰好处在分割线上的点,分为两种情况:①当分割线左右的点数量不相等时,将处在分割线上的点分配给点数少的那个子树;②当分割线左右的点数量相等时,将处在分割线上的点分配给离它最近的那个点所在的子树。之后重复该划分过程,直到将S划分成大小相等的m个不相交的部分即为分区Pi(1≤i≤m)。 注:KD树中每个分割维度的最小值、最大值和中位数构成了包含分区Pi的轴对齐边界框Bound(Pi),故原始空间记为∪Bound(Pi)(1≤i≤m),其中,Bound(Pi)∩Bound(Pj)=∅(i≠j)。另外,对每个分区Pi,其包含Pi内所有点vj的最小边界框为MinBound(Pi)={[dmin(vj,PSu),dmax(vj,PSu)]|vj∈Pi,u∈[1,q]}。 KD树划分示例图如图1a所示,采样数据集S={v1,v3,v4,v5,v6,v9,v11,v12,v15},第一次分区迭代时,mp=m=4,计算出x轴方向上的方差为7.65,y轴方向上的方差为10.62,因此使用y轴的中位数7划分,整个采样数据集S被划分成两个部分。此后,以类似的方式将这两部分递归划分,直到得到4个均匀的部分,即P1={v1,v2,v3}、P2={v4,v5,v6,v7}、P3={v8,v9,v10,v11}和P4={v12,v13,v14,v15}。由分区结果可以计算出Pi的最小边界框MinBound(Pi)(如图1b中灰色阴影部分),如MinBound(P1)={[2,6],[8,10]}。 (5)数据划分 在得到一组不相交的子空间Bound(Pi)后,D中的每个对象都可以根据Bound(Pi)分配到相应的分区Pi中,即利用映射后的样本数据间的分割来估计原始数据之间的分割。划分完成后,输出两表:分区信息表和数据信息表。分区信息表记录每个分区Pi的信息,包括Pi的分区IDpid和Pi的最小边界框MinBound(Pi);数据信息表记录每个点vi的信息,包括vi的IDvid、对应的分区IDpid和映射向量φ(vi)。 相似度矩阵是对任意两样本之间相似度信息的描述,其构造的好坏对最终聚类效果至关重要。现有的并行算法构建矩阵时计算所有数据间的距离,产生大量冗余计算,这严重制约了谱聚类算法的效率。基于此,本文采用t近邻稀疏化相似度矩阵,具体思想为:①局部t近邻搜索:并行计算每个Map分区内部样本数据的t近邻;②跨分区的t近邻搜索:提出优化的分区分配策略(OPA)将合格的数据分配给分区,进行跨分区的t近邻搜索,得到各样本数据的t近邻,同时,搜索过程中设计基于三角不等式的KD树剪枝策略以快速缩小搜索区域,避免无效计算;③获取相似度矩阵:计算数据间的相似度值并存储整个数据集的相似度矩阵。 (1)局部t近邻搜索 计算每个分区Pi中数据点之间的距离,并找到每个数据点vj∈Pi的局部t近邻结果。之后,将vj的t个最近的邻居vj.tNN、vj到其第t个最近邻居的距离vj.dt和vj的搜索范围vj.SR添加到数据信息表,Pi的搜索区域Pi.SR添加到分区信息表。其中,vj.SR={[d(vj,PSu)-vj.dt,d(vj,PSu)+vj.dt]|u∈[1,q]}表示vj的搜索范围,是一个将搜索区域限定在可能更新vj.tNN的潜在数据点的阈值;Pi.SR=∪vj∈Pivj.SR∪MinBound(Pi)表示Pi的搜索区域。 (2)跨分区的t近邻搜索 完成各分区内部的t近邻搜索后,在各个分区之间进行t近邻搜索。一旦某个数据vi满足d(vi,vj) 定理2OPA策略。设m为分区个数,将分区Pi的数据分配给分区Pj,则 (10) 式中i、j为分区下标。 此外,为避免将无效数据分配给分区导致冗余计算,本文设计了基于三角不等式的KD树剪枝策略,其具体过程为:①提出数据近邻点判断定理,对不属于分区Pi内的数据点vj,若其位于Pi的搜索区域Pi.SR之外,则对数据点vj进行剪枝,将vj与该分区内所有数据的相似度值记为0,否则依次计算各数据间距离,更新t近邻结果;②提出分区近邻点判断定理,对分区Pi,若其最小边界框与数据点vj(vj∉Pi)的搜索区域不相交,则将分区Pi从点vj的搜索区域中删除,且分区Pi内所有数据与数据点vj的相似度值记为0,否则依次计算各数据间距离,更新t近邻结果。 定理3数据近邻点判断。给定一个分区Pi,一数据点vj∉Pi,若vj的映射向量φ(vj)位于Pi的搜索区域Pi.SR之外,则∀v∈Pi,vj∉v.tNN。 证明已知φ(vj)位于Pi的搜索区域Pi.SR之外,则∃PSk∈PS,∀v∈Pi,有d(vj,PSk)>d(v,PSk)+v.dt或d(vj,PSk) 因此∀v∈Pi,vj∉v.tNN,即数据点vj不属于分区Pi内所有数据的t近邻。证毕。 定理4分区近邻点判断。给定一个分区Pi,一数据点v∉Pi,若MinBound(Pi)∩v.SR=∅,则有∀vj∈Pi,vj∉v.tNN。 证明因为∀vj∈Pi,∀PSu∈PS,MinBound(Pi)= {[dmin(vj,PSu),dmax(vj,PSu)]|vj∈Pi,u∈[1,q]},所以有dmin(vj,PSu)≤d(vj,PSu)≤dmax(vj,PSu)。 又因为MinBound(Pi)∩v.SR=∅,且v.SR={[d(v,PSu)-v.dt,d(v,PSu)+v.dt]|u∈[1,q]},所以∀PSu∈PS,有 d(v,PSu)-v.dt>dmax(v,PSu) 或d(v,PSu)+v.dt ⟹d(vj,PSu)≤dmax(vj,PSu) 或d(v,PSu)+v.dt ⟹|d(v,PSu)-d(vj,PSu)|>v.dt 由三角不等式又有∀vj∈Pi, d(v,vj)≥|d(v,PSu)-d(vj,PSu)|>v.dt ⟹vj∉v.tNN。证毕。 (3)获取相似度矩阵 对稀疏矩阵中的每个非零元素,计算数据点与其t近邻的相似度值,生成两个键值对 并行构建相似度矩阵的伪代码如算法1所示。 算法1并行构建相似度矩阵。 输入:顶点集V,度量距离函数d,近邻数t,分区数m; 输出:相似度矩阵S∈Rn×n。 1. for each partitionPido 2. for each vertexv∈Pido //计算v的t近邻、到第t个近邻的距离及v的搜索范围 3. computev.tNN,v.dtandv.SR 4. end for 5. computePi.SR=∪v∈Piv.SR∪MinBound(Pi) //获取Pi的搜索区域 6. end for 7. for each vertexv∈Pido //分区间数据分配 10. Assign (v,Ps) 11. end for 12. else 14. Assign (v,Ps) 15. end for 16. end if 17.end for 18. for each partitionPido 19. for each vertexv∈Pido 20. for each allocated vertexvjdo 21. ifv∈vj.SR then 22. ifd(v,vj)≤v.dtthen //用vj的搜索范围更新v的t近邻 23. updatev.tNN 24. end if 25. end if 26. ifvj∈v.SR then 27. ifd(v,vj)≤vj.dtthen //用v的搜索范围更新vj的t近邻 28. updatevj.tNN 29. end if 30. end if 31. end for 32. end for 33.end for 34.compute similarity 35.similarityToSymmetry () //调整相似矩阵为对称矩阵 36.MapReduce.Ruduce () 37.returnthe similar matrixS∈Rn×n//获得相似度矩阵 38.Function: Assign (v,Ps) //判断近邻点 39.ifφ(v)∈Ps.SR then 40. assignv toPs//数据近邻点判断 41.else ifMinBound(Ps)∩v.SR=∅ then 42. assignv toPs//分区近邻点判断 43.end if 由于稀疏相似矩阵是按行划分存储在分布式节点上的,且矩阵的加减操作对于每一行是独立的,矩阵的计算可以在各节点分布执行。并行计算特征向量主要分为3个步骤:①计算Laplacian矩阵:求出对角矩阵并通过变换矩阵对应位置元素的方式得到Laplacian矩阵;②正规化Laplacian矩阵:提出正规化定理,用元素对应相乘的方式代替矩阵相乘操作,优化Laplacian矩阵正规化过程;③求解特征向量:用Lanczos算法并行求解前k个最小特征值及其对应的特征向量。 (1)计算Laplacian矩阵 并行计算相似度矩阵W每行元素之和,得到对角矩阵D。由于对角矩阵除对角线以外的元素都为0,而相似度矩阵对角线上的元素都为0,因此,对相似度矩阵的非对角线元素进行取反,将对角阵的对角元素一一对应添加到取反后的相似度矩阵对角线上,得到Laplacian矩阵L。 (2)正规化Laplacian矩阵 提出正规化定理,将对角矩阵D的对角线元素其分发到各个节点上,各节点根据正规化定理将矩阵L的元素与对应的对角阵元素相乘,得到正规化矩阵L′。 定理5正规化定理。对于Laplacian矩阵L,其正规化后的矩阵L′仍为对称矩阵,且等于原矩阵L对应位置元素xij乘一个系数(标量)cicj,其中,ci为对角阵元素。 证明因为D为对角阵,故D-1/2也为对角阵;又因为L′=D-1/2LD-1/2=(D-1/2L)D-1/2,所以L′即为先求对角阵D-1/2右乘矩阵L作为中间结果,后用对角阵D-1/2左乘中间结果。由对角阵的性质可知,对角阵右乘一个矩阵就是用对角阵的对角依次与该矩阵对应行上的元素相乘,相当于对矩阵L依次做行变换,即 (11) 对角阵左乘一个矩阵,就是用对角阵的对角依次与该矩阵对应列上的元素相乘,相当于对矩阵依次做列变换,即 (12) 由此可以得出,某一矩阵左乘对角阵之后再右乘对角阵,相当于对对角阵左边的矩阵依次做行变换和列变换,即xij对应的系数为cicj,故有 (13) 因此,Laplacian矩阵的正规化操作可以通过矩阵对应位置元素乘一个系数(标量)的方式来实现。另外,因为L是对称矩阵,所以xij=xji,又因为cicj=cjci,所以cicjxij=cjcixji,即变换之后得到的L′依然为对称矩阵。证毕。 (3)求解特征向量 首先,将矩阵L′按行分割存放,每次迭代将要和矩阵相乘的向量发送到矩阵L′的位置,通过Lanczos算法并行计算向量和矩阵L′的乘积,得到三对角矩阵;然后,通过QR(orthogonal triangular)算法求出三对角矩阵的特征值和特征向量,且这些特征值和特征向量就是原Laplacian矩阵的特征值和特征向量近似值;最后,对特征值按由小到大的顺序排列,其对应的特征向量构成一个新的n×k阶特征向量矩阵Z并对其正规化。 并行求解特征向量的伪代码如算法2所示。 算法2并行求解特征向量。 输入:相似度矩阵S∈Rn×n; 输出:正规化特征向量矩阵T。 1.for each partitionPido 2. for each linee∈Pido 4. Lii=Dii//获取L的对角线元素 5. if Wij≠0 then 6. Lij=-Wij//获取L的非对角线元素 7. end if 8. if Lij≠0 then 10. end if 11. end for 12. end for 13.for each partitionPido 14. Lanczos (αi,βi) //调用Lanczos算法 15.end for 16.construct the multiplication result 17.QR (βi,γi) //QR分解 18.regularized eigenvector matrixT 19.MapReduce.Ruduce () //合并得到正规化特征向量矩阵 20.returnT 在对谱聚类算法的特征谱空间聚类时,初始簇中心的选取对聚类效率和正确率有很大影响,现有的并行谱聚类算法采用随机选取的方式,容易引起算法初始簇中心敏感的问题。考虑到MA算法具有对初值不敏感和求解精度高的特点,故在并行聚类过程中引入MA算法,但该算法在迭代的过程中种群的多样性会降低,可能出现早熟收敛,为此,本文提出混沌蜉蝣优化算法(CMO)用于获取初始簇中心,然后对特征空间进行并行聚类,最后得到最终聚类结果。 3.4.1 CMO算法 CMO算法获取初始簇中心的具体过程为:①初始化种群:用Sin混沌序列初始化种群;②更新位置:提出速度更新参数sr1、sr2,改进原有的速度更新公式,更新蜉蝣速度与位置;③判断早熟收敛:提出蜉蝣群体适应度方差的早熟收敛判断机制,并添加混沌扰动帮助算法跳出局部最优,迭代终止后得到最佳的初始簇中心。 (1)初始化种群 混沌变量具有随机性、遍历性和规律性的特点,将其运用于优化搜索可以保持种群的多样性,帮助算法跳出局部最优,从而提高算法的全局搜索能力。本文用Sin混沌序列对种群进行初始化,步骤描述如下: 步骤1随机生成(-1,1)内的初始值Z0,记iter=0; 步骤2对式(6)进行迭代,得到Z序列,iter自增1; 步骤3若达到最大迭代次数,结束程序,同时存储最终产生的Z序列。 (2)更新位置 提出速度更新参数sr1、sr2,代替原来的随机数r1、r2,更新蜉蝣速度与位置,同时记录蜉蝣的个体极值对应的位置pbest和全局极值对应的位置gbest。 定理6速度更新参数sr1、sr2。在速度更新公式中嵌入Sin混沌变量,雄性蜉蝣的速度为: (14) 雌性蜉蝣的速度为 (15) 式中sr1、sr2为从Sin混沌中随机选取的两个混沌数。 证明由于Sin混沌映射在-1到1之间波动,均匀分布的随机数也在[-1,1]之间,随机选取的混沌数sr1、sr2可以用来代替均匀分布的随机数r1和r2。同时,比起单纯采用随机数,嵌入Sin混沌序列更有利于保证蜉蝣运动过程的随机性和遍历性,故参数sr1、sr2可用于更新蜉蝣速度。证毕。 (3)判断早熟收敛 提出群体适应度方差σ2,判断算法是否早熟收敛,若早熟收敛,则以搜索停滞的解为基础产生Sin混沌序列,对部分陷入局部最优的蜉蝣进行混沌扰动,避免算法陷入局部最优,提高全局搜索能力和寻优精度。添加混沌扰动的具体步骤如下: 步骤1根据式(6)迭代生成混沌变量; 步骤2将混沌变量载波到原变量的解空间; 步骤3按式newX′=(X′+newX)/2对蜉蝣的位置进行混沌扰动,其中:X′为需要进行混沌扰动的蜉蝣位置,newX为产生的混沌扰动量,newX′为混沌扰动后的蜉蝣位置。 (16) 式中f为归一化因子,其作用是限制σ2的大小, (17) 证明σ2越小,表示各蜉蝣的适应度值越接近平均适应度,即偏离程度越小,此时种群趋于收敛;反之,σ2越大,表示各蜉蝣的适应度值越远离平均适应度,即偏离程度越大,则此时种群更容易处于随机搜索状态。因此,群体适应度方差σ2可以反映种群中所有雄蜉蝣的“收敛程度”。证毕。 CMO算法获取初始簇中心的步骤如下: 步骤1输入Laplacian矩阵降维之后的结果矩阵,待聚类个数K,最大迭代次数Imax,群体适应度方差临界值∂,混沌搜索迭代次数M。 步骤2采用Sin混沌映射初始化产生两组数目相同的(K个)的初始种群,初始种群分别代表雄性蜉蝣、雌性蜉蝣,初始化其位置并设定参数,然后用Sin混沌映射函数产生混沌随机序列S1、S2。 步骤3每个雄性蜉蝣根据选取的中心按照最小距离原则划分聚类数据集,计算适应度值,并根据式(14)更新雄性蜉蝣的速度与位置,同时记录每个雄性蜉蝣的个体极值对应的位置pbest和全局极值对应的位置gbest。适应度函数采用聚类指标DBI指数的计算公式: (18) 步骤4根据式(15)更新雌性蜉蝣的速度与位置。 步骤5进行交叉,产生雄性和雌性后代,用产生的具有最优适应度的新后代取代具有最劣的适应度的父代蜉蝣。 步骤6判断是否满足精度要求或者达到最大迭代次数,若是,转步骤9,否则转步骤7。 步骤7计算雄性蜉蝣的群适应度方差σ2。若σ2<∂,则转步骤8,否则转步骤3。 步骤8若算法早熟收敛,利用混沌搜索更新蜉蝣位置来跳出局部最优,完成后转步骤3。 步骤9将得到的最佳位置作为k-means算法的初始簇中心。 3.4.2 并行k-means聚类 用CMO算法获取初始簇中心后,进行并行k-means聚类,此过程包括Map阶段和Reduce阶段。在Map阶段,计算每个数据点vi到初始聚类中心Cj(1≤j≤k)的距离,将该样本点分配给距离最小的聚类中心,以 PSC-MO算法的具体实现步骤如下: 步骤1调用DPS数据分区策略,将原始数据集合理划分为大小相同的文件块。 步骤2启动MapReduce任务,调用算法1获得相似度矩阵,并将结果存入分布式文件系统HDFS中。 步骤3启动新的MapReduce任务,调用算法2得到正规化特征向量矩阵Z,将结果存储到Hadoop分布式文件系统(Hadoop Distributed File System,HDFS)中。 步骤4再次启动新的MapReduce任务,先调用CMO算法获取初始聚类中心,然后进行k-means聚类,迭代直至获得最终聚类结果。 PSC-MO算法时间复杂度主要由数据划分、并行构建相似度矩阵、并行计算特征向量以及并行聚类4部分组成,分别记为T1、T2、T3和T4。 (1)数据划分阶段,对于KD树分区,需要采样后执行映射操作,然后将整个空间分割。假设选出l个支撑点,S为样本集大小,m为分区数,执行映射的时间复杂度为O(Sl),将空间划分为m个分区的时间复杂度为O(SlogSlogm),故数据划分阶段的时间复杂度为T1=O(S×(l+logSlogm))。 (2)并行构建相似度矩阵阶段,将KD树用于t近邻搜索,避免遍历所有点,且用剪枝策略避免其在高维数据上陷入维度诅咒,假设数据维度为d,则计算整个数据集之间的距离时间复杂度为O(ndlogn/m),通过保留大小为t的最大堆稀疏化矩阵,故构建稀疏相似度矩阵的时间复杂度为T2=O((ndlogn+nlognlogt)/m)。 (3)并行求解特征向量阶段,Laplacian矩阵正规化的时间复杂度为O(nt/m),用Lanczos计算矩阵与向量相乘的时间为nt,求前k个特征向量的时间复杂度为O(knt/m+k2n),故并行求解特征向量阶段的时间复杂度为T3=O(nt/m)+O(knt/m+k2n)。 (4)并行聚类阶段,假设待聚类数目为k,M为迭代次数,计算任意点与当前k个聚类中心的距离,时间复杂度为T4=O(nMk2/m)。 因此,PSC-MO算法的时间复杂度为TPSC-MO=T1+T2+T3+T4。大数据环境下,由于S 对于PSC[21]算法,在构造相似度矩阵阶段需要扫描整个数据集,计算欧式距离并迭代地重构最大堆,该阶段的时间复杂度为O((n2d+n2logt)/m);在并行求解特征向量阶段,Laplacian矩阵正规化的时间复杂度为O(n3/m),设p为特征求解中Arnoldi长度,q为Arnoldi迭代次数,则求前k个特征向量的时间复杂度为O(p3q)+(O(pn/m)+O(nt/m))×O(q(p-k)),故并行求解特征向量阶段的时间复杂度近似为O(n3/m);并行聚类阶段时间复杂度为O(nMk2/m)。因此,算法总时间复杂度为TPSC=O((n2d+n2logt)/m)+O(n3/m)+O(nMk2/m)。 对于PSCA[22]算法,构造相似度矩阵的时间复杂度为O((n2d+n2logn)/m);在并行求解特征向量阶段,Laplacian矩阵正规化的时间复杂度为O(n3),Lanczos算法矩阵与向量相乘的时间复杂度为O(n2),并行求解特征向量阶段的时间复杂度近似为O(kn2/m+k2n);并行聚类阶段时间复杂度与PSCA算法基本相同。因此,PSCA算法时间复杂度为TPSCA=O((n2d+n2logn)/m)+O(n3)+O(kn2/m+k2n)+O(nMk2/m)。 对于PSC-KD[23]算法,构造相似度矩阵时采用KD树索引查找近邻,其时间复杂度为O((ndlogn+n2logn)/m),但最坏情况下(即数据维度过高)可能达到O((n2d+n2logn)/m);求解特征向量和并行聚类阶段与PSCA算法基本相同。因此,PSC-KD算法时间复杂度TPSC-KD=O((ndlogn+n2logn)/m)+O(n3)+O(kn2/m+k2n)+O(nMk2/m)。 另外,由于nlogn 为验证PSC-MO算法的性能,本文设计了相关实验。实验采用的分布式集群包含1个Master节点和7个Slaver节点。各节点的硬件配置均为Intel(R)Core(TM)i7-9750H CPU、16 GB DDR4 RAM、1TB SSD,且各节点处于同一局域网中,通过500 Mb/s以太网进行通信。软件配置为Ubuntu 16.04.7,Hadoop 2.7.5和JDK 1.8.0。 在算法可行性分析中,需要在规模不同的数据集上验证PSC-MO算法的可行性;在算法性能比较中,用规模较大但维度不同的数据集评估PSC-MO算法的性能。因此,本文采用5个数据集,分别是规模较小的Corel[44]和规模较大的RCV1[45],covtype[46],kddb[47]和picasa[48]。Corel是科雷尔公司收集整理的图像数据集,包含10类共1 000张图像;RCV1是路透社提供的新闻语料库,为方便实验对比,删除了多重标记的数据和小于500个文档的类,最终获得了103类共计193 844个文档,47 236个属性;covtype记录了美国科罗拉多州不同地块的森林植被类型,该数据集共有581 012个实例,每个实例具有54个属性;kddb是KDD CAUP 2010的问题训练集,实验采用的数据集是胜利者转换过的版本,共包含826 048条数据和29 890 095条特征,具有数据维度高的特点;picasa来自于Google的picasa图片数据集,该数据集有1 730 897条实例,144个属性,具有数据量大的特点。数据集的详细信息如表2所示。 表2 实验数据集 4.3.1 NMI 标准化互信息(Normalized Mutual Information,NMI)利用互信息来衡量数据分布的吻合程度。为验证PSC-MO算法的聚类效果,本文采用NMI作为聚类质量评估标准,其定义为: (19) 式中:向量X为聚类得到的类别序列构成的n维向量;向量Y表示真实样本标签构成的n维向量,n为样本个数。I(X,Y)表示X与Y的互信息,H(X)和H(Y)分别表示X和Y的香农熵。NMI的取值区间为[0,1],值越大表明聚类质量越高。 4.3.2 加速比 加速比是指同一任务在串行处理和并行处理下消耗的时间的比率。为评估PSC-MO算法并行处理大数据的能力,本文采用加速比衡量算法的效果和并行性能,加速比定义为: (20) 式中:TS、TP分别为算法串行运行时间和并行运行时间;Speedup越大说明算法的并行化程度越高。 4.3.3 Efficiency 并行效率(Efficiency)是指并行系统的加速比和执行任务所用计算节点数的比率。为评估PSC-MO算法的可扩展性,本文采用Efficiency衡量算法的并行效率,Efficiency定义为: (21) 式中:SN为算法的加速比;N为集群中计算节点数量。η的值越接近1说明算法对集群的利用率越高。 4.4.1 CMO算法可行性分析 为验证CMO算法的可行性和优越性,在4个不同的基准测试函数上对粒子群算法(Particle Swarm Optimization Algorithm, PSO)、遗传算法(Genetic Algorithm, GA)、差分进化算法(Differential Evolution Algorithm,DE)、蜉蝣算法(Mayfly Algorithm,MA)[33]和CMO算法进行仿真实验。实验所用的基准测试函数包括单峰函数和多峰函数,其具体信息如表3所示。为避免参数随机性对最终效果的影响,实验中将所有算法的参数设置相同,通过多次运行实验选取结果较好的数值作为参数,最终选取种群规模N=40(MA和CMO算法中雄性和雌性个体分别为20),正吸引系数a1=1、a2=1.5,能见度系数β=2,舞蹈系数d=0.1,随机飞行系数fl=0.1,最大迭代次数Maxiter=1 000,维度d分别为10、50、100。为对算法进行统计学分析,选取各算法在基准测试函数上独立运行60次的实验结果,将各算法的平均值和标准差作为评价指标。基准测试函数优化结果如表4所示。 表3 基准测试函数 表4 基准测试函数优化结果比较 从表3可以看出,各算法在4个测试函数上的寻优精度和寻优稳定性随着维度增大而降低,且CMO算法多次寻优的平均值和标准差相比MA算法均更小,始终拥有更好的寻优性能。在优化单峰函数F1、F2时,CMO算法不论是在10维、50维还是100维,求解精度和求解稳定性相比PSO、GA、DE、MA算法都有一定幅度的提升,甚至在维度为10时平均值能达到理论最优解0,标准差最小,比MA算法提升了20个数量级以上。在优化多峰函数时,CMO算法在不同维度下的求解精度均更高,其中,优化F3时平均差分别达到了6.1285E-57、2.6429E-26和7.2687E-12,标准差达到了9.3891E-57、6.2682E-27和3.2629E-12,取得了较为理想的结果,这也说明本文的改进策略是可行有效的。另外,随着维度逐渐增大,各算法的求解精度和稳定性都有所降低,而CMO算法则变化较小,尤其是在多峰函数F8上,维度为100时算法的平均值和标准差分别达到了2.9752E-03和1.9529E-03,依然接近理论最优解,表现出了极强的稳定性。这是由于单峰函数在求解区域内只有一个极值,寻优相对容易,故各算法的寻优结果差异较不明显。而对多峰函数进行寻优的过程中,其求解区域内存在大量局部极值点,未作改进的MA算法易陷入局部最优,其求解精度不高。相比之下,CMO算法充分利用混沌运动的随机性、遍历性保证了种群的多样性和搜索的遍历性,在迭代过程中始终保持较强的搜索能力,这就在保证局部搜索能力的同时加强了算法的全局寻优能力。此外,CMO算法在MA算法的基础上增加了早熟收敛判断机制,用Sin混沌搜索有效地帮助算法跳出局部最优点,从而更精确地找到全局最优值。因此可以得出,CMO算法具有可行性,且鲁棒性和稳定性优于其他对比算法。 4.4.2 PSC-MO算法可行性分析 为验证PSC-MO算法在大数据环境下并行聚类的可行性,采用算法的加速比来进行衡量,对PSC-MO算法在Corel、RCV1、covtype、kddb、picasa 5个数据集上进行测试。为避免实验结果的偶然性,算法在每个数据集上独立运行5次,取其平均值,实验结果如图2所示。 从图2可以看出,随着节点数逐渐增加,PSC-MO算法在5个数据集上的加速比基本呈上升趋势,且数据集规模越大,PSC-MO算法加速比的上升趋势愈加明显,表现出其良好的可行性与有效性。其中,当节点数为2时,PSC-MO算法在五个数据集上的加速比差距较小,在规模最小的Corel数据集上最小;当节点数为4时,PSC-MO算法的加速比分别比在一个节点上增加了1.13、1.47、2.28、2.61、2.87;当节点数为8时,算法加速比达到最高,分别为3.19、3.78、5.38、6.74、7.51,比在6个节点上增加了0.18、0.24、0.68、1.51、1.85。这是由于PSC-MO算法设计了DPS策略,在方差最大的维度上划分数据并分配均匀的数据给各节点,减少了节点间的通信时间,保证了各节点间负载均衡,极大地提高了并行处理效率。此外,在构建相似度矩阵时,采用OPA策略将合格的数据分配给分区并对数据点和分区进行剪枝,避免了冗余计算,减少了系统读写和传输数据占用的时间,节点间交互较少,一定程度上提升了算法的并行性能,且数据规模越大,减少冗余计算的优势被逐渐放大,PSC-MO算法的加速比提升更大。这也表明PSC-MO算法适用于大数据,且在规模较大的数据集上效果尤为明显。 4.5.1 聚类效果 为评估PSC-MO算法的聚类效果,将NMI值作为评价指标,将PSC-MO算法分别与不使用CMO优化的PSC-NOMO、PSC-KD、PSC算法在RCV1、covtype、kddb、picasa 4个数据集上进行对比实验。另外,为避免t值的选取影响实验结果准确性,在各数据集上分别取不同的t值,每次测试独立运行5次,取5次NMI的均值作为实验结果。实验结果如图3所示。 从图3可以看出,随着t近邻数的不断增加,各算法的NMI值先增加后减少,在同一数据集上相同t值达到NMI最大值,并且PSC-MO算法在不同数据集上的NMI值始终保持最高,表现出良好的聚类效果。其中,在数据量较小但类别数较多的数据集RCV1上(如图3a所示,t值为60时PSC-MO算法的NMI值达到了0.501,分别比PSC-NOMO、PSC-KD、PSC算法高出了0.104、0.138、0.159;在数据集covtype、kddb上(如图3b和图3c),各算法分别在t=80、t=120时聚类效果最好,PSC-MO算法的NMI值最高甚至达到了0.764;在数据量最大的数据集picasa上(如图3d),在t值为200时PSC-MO算法的NMI值为0.627,分别比PSC-NOMO、PSC-KD、PSC算法高出了26.92%、48.23%、46.84%。出现这种现象主要有两个原因:①PSC-MO算法采用了DPS策略对数据分区,尽可能将相似度大的数据划分到同一计算节点上,一定程度上减少了错误划分的可能,间接提升了聚类效果;②选取的t值太小不能包PSC-KD含足够多的数据间的相似信息,t值太大可能包含过多的信息,这都会使得聚类时寻优变得更加困难,从而影响算法的聚类效果,但PSC-MO算法在对特征谱空间聚类时,设计了CMO算法寻找最佳的初始聚类中心,提高了算法的全局搜索能力,从而提高了聚类质量。对于PSC-NOMO算法,仅是采用DPS策略对数据分区,并未改进最后聚类的过程,算法的聚类效果只有小幅度的提升。同样地,PSC-KD、PSC算法也只是简单地并行化k-means聚类过程,极易受噪声数据的影响,聚类效果并不理想。 4.5.2 算法运行时间 为验证PSC-MO算法的时间复杂度,在上述4个数据集上对PSC-MO、PSCP(不包含KD树剪枝的PSC-MO算法变体)、PSCA和PSC-KD算法分别进行5次测试,取其平均值,得到各算法的运行时间(如图4)。 从图4可以看出,随着数据规模和数据维度的增大,各算法的运行时间也不断增加,但相较于PSCP、PSC-KD和PSCA算法,PSC-MO算法在4个数据集上的运行时间均有所下降,尤其是在规模较大的数据集kddb、picasa上降低的幅度更为明显。其中,在kddb数据集上,PSC-MO算法的运行时间降低幅度最大,分别比PSCP、PSC-KD和PSCA算法降低了57.56%、64.79%和69.74%;在规模较小的covtype数据集上降低的幅度最小,但也分别降低了12.04%、34.45%和47.04%。造成这种结果的主要原因有4点:①PSC-MO算法的DPS策略增加了处理数据集的时间,在小规模数据集上执行该策略耗费的时间小于其对算法时间开销的优化,但随着数据集规模的增大,DPS策略消耗的时间所占比重逐渐降低,数据规模足够大时其对算法的整体性能影响几乎可以忽略,故PSC-MO算法在大规模数据集上效果显著;②PSC-MO算法在耗时最多的并行构建相似度矩阵过程中,采用KD树索引并提出了合理的剪枝策略,避免了冗余计算,加快了搜索t近邻的速度,极大地减少了算法的运行时间;③PSC-MO算法对Laplacian矩阵正规化的优化避免了矩阵的直接相乘操作,减少了时间开销;④PSC-MO算法利用CMO算法可以找到较为合适的初始聚类中心位置,减少算法迭代次数,从而有效地降低了算法的运行时间。相比之下,未用KD树剪枝策略的PSCP算法和PSC-KD算法存在许多额外的非t近邻数据间的计算,该过程需要大量的时间开销,尤其是在数据维度高的kddb数据集上,PSCP算法和PSC-KD算法的劣势更加明显;另外,PSC-KD算法与PSCA算法在Laplacian矩阵正规化和最终聚类迭代过程中也需要消耗大量的计算资源。整体来说,相较于PSCP、PSC-KD和PSCA算法的运行时间,PSC-MO算法展现了出色的性能。 4.5.3 算法加速比 为评估PSC-MO算法在大数据环境下的并行性能,在上述4个数据集上对PSC-MO、PSCP(不包含KD树剪枝的PSC-MO算法变体)、PSCA和PSC-KD算法分别进行5次测试,取运行时间的平均值作为实验结果,然后计算加速比,最终的实验结果如图5所示。 从图5可以看出,随着节点数的增加,各算法的加速比也逐步增加,并且PSC-MO算法在规模较大的kddb、picssa数据集上始终拥有最高的加速比。在处理RCV1这样规模相对较小的数据集时(如图5a),各算法加速比差别不大,当节点数为2时,PSC-MO、PSCP算法的加速比分别为1.36、1.41,略小于PSCA和PSC-KD算法(1.49、1.57),但随着节点数目增多,PSC-MO、PSCP算法的加速比超越了PSCA和PSC-KD算法,且各个算法的加速比增长趋于平缓。这是由于在数据集的规模较小时,各节点间的通信时间占算法的很大一部分,而通过并行化运算获得的运行速度提升却极为有限从而导致了加速比较小;当节点数量增加时,相比其他算法,用DPS分区策略的PSC-MO、PSCP算法可以有效控制节点之间的负载均衡,因此PSC-MO、PSCP算法的加速比略高于其他算法。此外,可以看出,在处理kddb以及picasa这样规模相对较大的数据集时(如图5c和图5d),3个对比算法的加速比最终趋于稳定,而PSC-MO算法运行的加速比随着节点数的增加而逐渐增加,尤其是在picasa数据集上,当节点数分别为2、4、6、8时,PSC-MO算法运行的加速比分别为1.95、3.87、5.66、7.51,基本接近线性增长,并且PSC-MO算法始终具有最高的加速比,而未进行KD树剪枝的PSCP算法的加速比始终小于PSC-MO算法的加速比。这是由于PSC-MO算法的分区策略保证了各节点间的负载均衡,而搜索t近邻时的KD树剪枝策略可以一定程度上减少节点间的通信开销,并且随着数据规模的增大,算法通过高效的并行化运算减少总体运行时间的优势被逐渐放大,从而有了更大的加速比。因此,PSC-MO算法在大数据环境下拥有更好的并行性能。 4.5.4 算法并行效率 为评估PSC-MO算法在大数据环境下的可扩展性,在上述4个数据集上对PSC-MO、PSC、PSCA和PSC-KD算法分别进行测试,分别比较用不同节点数处理各算法的并行效率。同时,为避免实验结果的偶然性,每次测试独立运行5次,取5次Efficiency(并行效率)的均值作为实验结果。最终的实验结果如图6所示。 从图6可以看出,随着节点数的增加,各算法的并行效率均呈下降趋势,但PSC-MO算法在数据量更大的数据集covtype、kddb、picssa上始终保持最高的效率,且下降幅度较小,表现出良好的系统可扩展性。其中,在数据量较小的数据集RCV1上(如图6a),各算法差异较不明显,当节点数较少时PSC-MO算法的并行效率要低于其他算法,但当节点数达到8时,PSC-MO算法的效率超越了其他算法,分别比PSC、PSCA和PSC-KD算法高出了17.51%、24.60%、6.78%;在数据集covtype上(如图6b),PSC-MO算法的效率要明显高于其他算法,当节点数为8时,分别高出了30.47%、45.58%、20.35%;在数据集kddb上(如图6c),当节点数达到8时,PSC-MO算法的效率分别比PSC、PSCA和PSC-KD算法高出了52.03%、104.79%、63.96%;在数据集kddb上(如图6d),PSC-MO算法的效率依然高于其他算法且表现得相当平稳,当节点数为2、4、6、8时其并行效率分别达到了97.54%、96.74%、94.27%、93.82%,均保持在90%以上。产生这种结果的主要原因是:①PSC-MO算法采用了DPS策略,用KD树将整个数据空间分割成若干个均匀的子空间,节点间负载达到均衡,减少了节点间互相等待的时间。同时,通过对数据采样、选择支撑点的方式减少了计算成本,这都有效提升了算法并行效率,但在小规模数据集上,由于DPS策略将数据分布到各节点、任务调度等会造成通信时间增多,而通过该策略减少的时间开销却极为有限,故在小数据集上效果不太明显;②PSC-MO算法在计算相似度矩阵时采用了OPA策略分配数据,并设计了合理的剪枝策略对数据和分区进行剪枝,避免了冗余计算,大大减少了节点间传输数据的时间开销,一定程度上提高了算法并行效率,且随着数据集规模的增大,该策略对算法效率提升的优势愈加明显。相比之下,PSC、PSCA算法分配数据时,未考虑数据的分布特性,节点数较多时将数据分布到各节点会导致通信时间增加,尤其是在小规模数据集上,其通信时间比重大大增加,从而降低算法并行效率;而PSC-KD算法虽然采用了KD树索引结构,但搜索t近邻时未提出有效的方法,数据规模过大时易陷入性能瓶颈。因此,PSC-MO算法对集群的利用率更为稳定,拥有较强的系统可扩展性。 为弥补大数据环境下并行谱聚类算法的不足,本文设计并实现了一种新的并行谱聚类算法PSC-MO。首先,提出了DPS策略划分数据,解决了各节点间负载不均衡的问题;其次,在构建稀疏相似矩阵过程中,提出了OPA策略和基于三角不等式的KD树剪枝策略以进行跨分区的t近邻搜索,既减少了通信开销又降低了计算成本;然后,提出了正规化定理,通过元素对应相乘的方式代替矩阵相乘以优化Laplacian矩阵正规化过程,进一步减少了时间开销;最后,提出混沌蜉蝣优化算法用于k-means并行聚类,有效避免了算法的初始化敏感问题。此外,为验证PSC-MO算法的性能,本文在4个数据集上分析并比较了PSC-MO算法与其他算法的聚类效果、运行时间、加速比和并行效率。实验表明,PSC-MO算法不仅具有良好的聚类效果,还在大规模数据集上表现出了良好的数据和系统可扩展性。 虽然PSC-MO算法在大数据环境下表现出良好的性能,但算法并未实现t近邻数、特征值数和后期聚类数的自动调优,这些不足也将是未来的研究方向。此外,未来也将尝试将PSC-MO算法用于更多的大数据应用场景中,充分发挥其在聚类性能上的优势。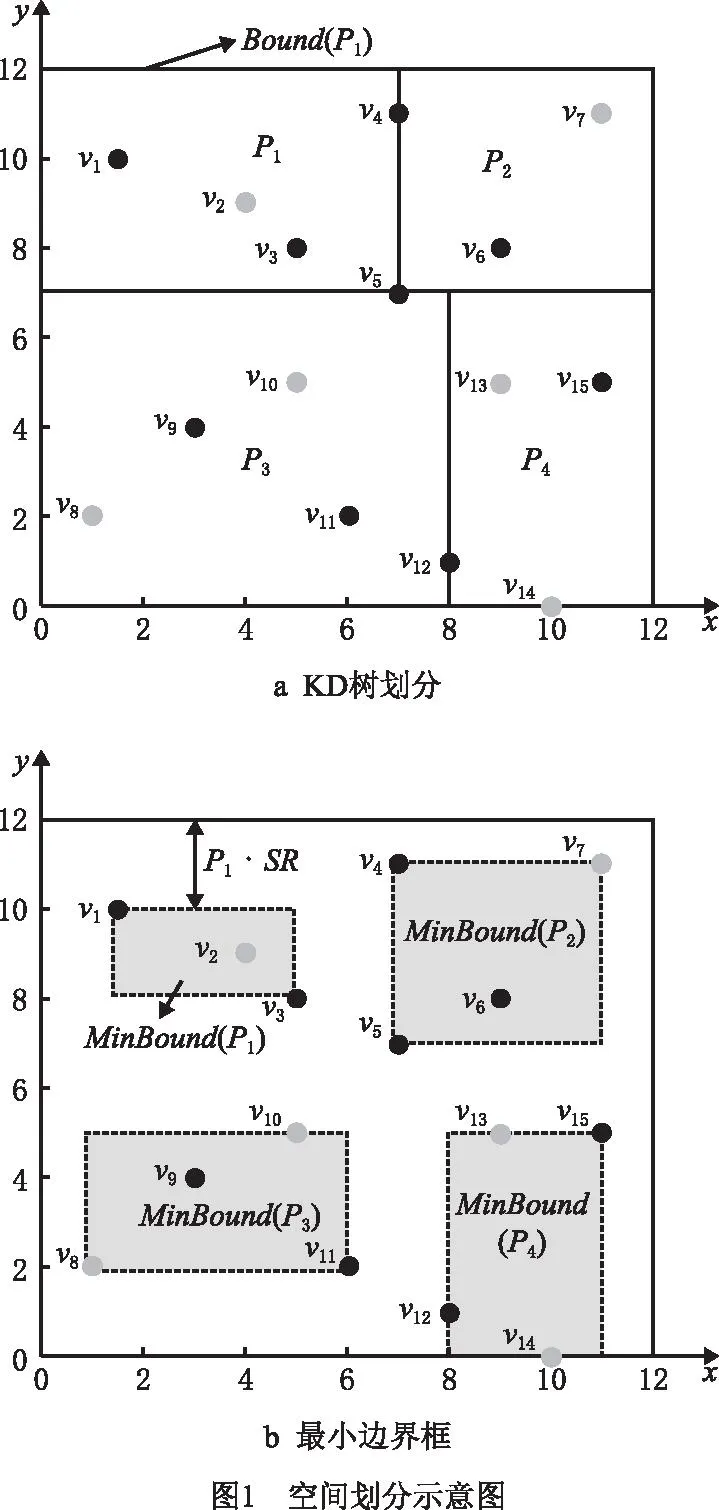
3.2 并行构建相似度矩阵

3.3 并行计算特征向量
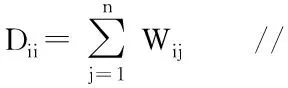
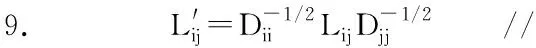
3.4 并行聚类

3.5 PSC-MO算法流程
3.6 算法时间复杂度分析
4 实验结果与分析
4.1 实验环境
4.2 实验数据

4.3 评价指标
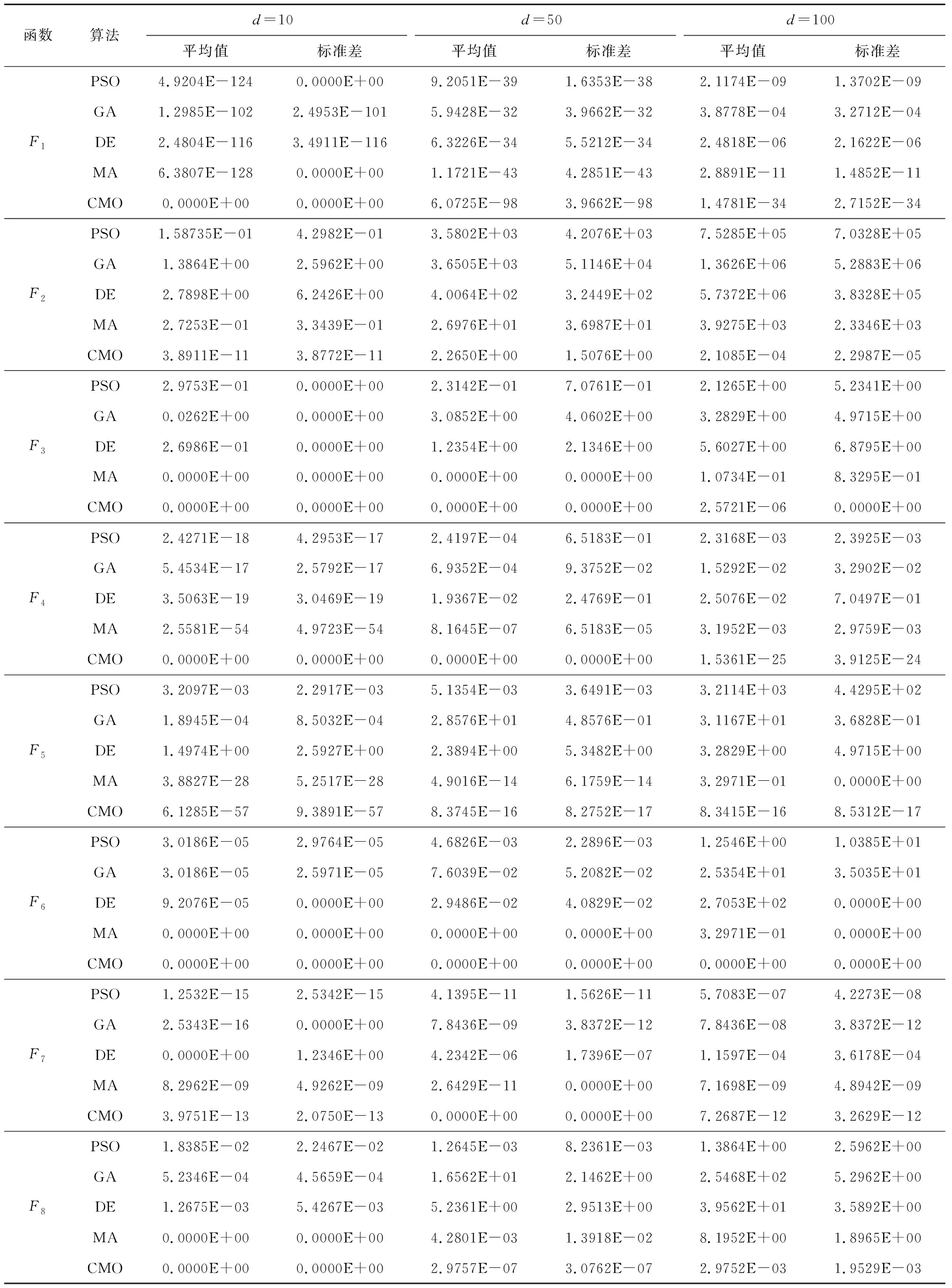
4.4 算法可行性比较分析

4.5 算法性能比较分析


5 结束语
