EPS 电能转换系统的有源阻尼解耦控制策略研究
2024-01-12程福泉杨朝廷丁进伟
程福泉,杨朝廷,刘 薇,张 烨,丁进伟
(中国长江电力股份有限公司溪洛渡水力发电厂,云南省昭通市 657300)
0 引言
传统EPS 的拓扑结构为前级整流单元充电,后级逆变单元放电。由于PWM 整流器具有电能双向传输能力,可将EPS中整流和逆变单元合二为一,优化系统电能转换效率。根据PWM 直流侧储能元件的不同可将其分为电压源型PWM 整流器(Voltage Source Rectifier,VSR)和电流源型PWM 整流器(Current Source Rectifier,CSR)。CSR 具有直流降压输出能力,稳定性高等特点[1-3],但实际直流侧一般不是纯阻性负载,电容性质负载的出现使CSR 变成非线性的强耦合系统,此时经典控制器如PID 控制的设计将变得复杂,同时参数整定也较难实现[4-5]。基于微分几何理论的线性化控制方案得到了较好的应用,通过非线性系统坐标变换及状态反馈,实现解耦控制,系统有较好的稳态性能及动态输出特性[6]。针对模型中d、q 轴耦合影响,文献[7]采用基于反步法的非线性控制策略,实现直流电流的稳定控制,但其运算复杂,应用范围小;文献[8]则采用了一种前馈解耦控制方法,消除了系统的非线性、强耦合特性;针对CSR 交流侧LC 滤波器易产生谐振的问题,文献[9]、文献[10]提出无源阻尼控制方案,直接在LC 回路中串并联电阻实现谐振尖峰抑制,但系统的有功损耗增加。目前有学者提出在控制回路中通过引入阻尼反馈回路实现谐振抑制,称为有源阻尼控制方案,有效避免了阻尼电阻产生的损耗。例如,利用自适应陷波器和电容电压反馈回路实现LC 回路谐振抑制,提高了系统动态性能,但控制器参数的整定步骤增加[11-12]。文献[13]分析和对比了CSR 交流侧电感、电容反馈对LC 谐振的影响,提出了一种适用于低开关频率下谐振抑制的有源阻尼方法;针对CSR 直流侧电流纹波的抑制,文献[14]通过不同模式下调制策略的优化以减小输出电流纹波;文献[15]则提出直流电流最优控制方案优化输出电流纹波,相比于调制方案,采用控制的方案优化CSR 输出电流纹波更为简便。综上,设计经济、高效的控制策略使CSR 更加契合地应用于各大场合,具有较大的现实意义。
本文综合分析了电容电压反馈和电感电流反馈对交流侧LC 滤波器谐振的影响,提出了一种组合型有源阻尼解耦控制策略。该控制策略将d轴定向于交流侧电容电压矢量进行解耦,简化CSR 数学模型;其次,设计电感电流反馈增益系数提高系统的谐振频率、设计电容电压反馈增益系数改善系统阻尼比,二者结合可灵活地优化系统性能;直流侧则采用状态反馈控制以稳定直流输出,调节d 轴开关分量可实现系统网侧单位功率因数运行。最后,通过仿真和实验对所提控制策略进行了有效性验证。
1 带容性负载CSR 的数学模型
带容性负载的三相CSR 拓扑结构如图1 所示,其中ek(k=a,b,c)为三相电压源、isk(k=a,b,c)为网侧电流、ik(k=a,b,c)为整流桥输入电流、uck(k=a,b,c)为交流侧电容电压,Lac与Cac构成网侧二阶滤波器;S1~S6是IGBT 功率开关管,并串接有二极管,实现直流侧回流反阻断;Df为续流二极管,大电感Ldc是实现AC/DC 转换的关键器件;Cdc和RL并联构成等效容性负载,io为输出电流,uo为输出电压,udc为整流桥输出电压。

图1 带容性负载的CSR 拓扑结构图Figure 1 CSR topology with capacitive load
忽略开关损耗,由基尔霍夫电压电流定律可得:
由于直流侧串联大电感,需防止直流侧出现开路状态。定义三值逻辑开关函数如下:
当σk=+1 表示CSR 上桥臂导通,当σk=0 表示CSR 上下桥臂全导通或者全关断,当σk=-1 表示CSR 下桥臂导通。
三值逻辑下,整流桥输入电流、整流桥输出电压分别为:
经Park 变换,d-q 坐标系下CSR 数学模型为:
其中,σd、σq分别表示三值逻辑开关函数的d 轴和q 轴分量;ed、eq、isd、isq、ucd、ucq分别表示网侧电压、网侧电流和交流侧电容电压的d 轴和q 轴分量;ω表示电网电压基波角频率。
利用d 轴定向于交流侧电容电压矢量,即ucq=0,消除耦合项,简化控制器设计,由于ωLac、ωCac很小,可忽略,式(5)、式(6)简化为:
2 组合型有源阻尼控制
针对CSR 的谐振问题,目前最为广泛的是采用无源阻尼的方法,即在交流侧滤波电感或电容上并联或串联电阻从而抑制谐振,如图2 所示。无源阻尼方法简便,但会造成电能损耗,可以利用滤波器中变量的反馈来抑制谐振同时避免无源阻尼的电能损耗,提高系统电能转换效率。
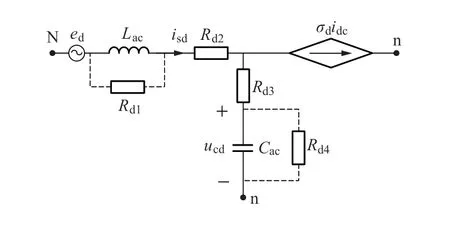
图2 无源阻尼控制方案Figure 2 Passive damping control scheme
反馈变量可能包含电感电流、电感电压、电容电流、电容电压。不同的反馈变量具有不同的控制效果,本文选取电感电流和电容电压组合反馈形式进行讨论。如图3 所示,为组合型有源阻尼控制框图。
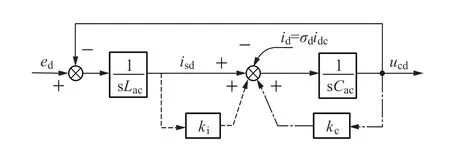
图3 组合型有源阻尼控制方案Figure 3 Combined active damping control scheme
由图3 归纳出在不同反馈下传递函数表达式如下:
采用电感电流反馈(ICF)时:
采用电容电压反馈(CVF)时:
采用电感电流反馈(ICF)与电容电压反馈(CVF)组合时:
当采用ICF 时,通过设计电感电流反馈增益系数ki可调节系统谐振频率,但无法改变系统阻尼比;当采用CVF 时,通过设计电容电压反馈增益系数kc,可调节系统阻尼比,但无法改变系统谐振频率;为同时调节系统谐振频率和阻尼比,优化系统性能,可以采用组合型有源阻尼控制,通过设计合理的反馈增益系数ki和kc以达到系统设计要求。
2.1 反馈系数设计
由于谐振频率主要是由ICF 的反馈增益决定,所以可以通过期望的谐振频率设计ki,ICF 传递函数表达式为:
为抑制谐振,主要谐波幅频增益σs应低于0dB,取σs=-5dB,ωs为期望的主要谐波频率,一般设置为系统谐振频率ωn的2 倍,因此,幅频增益应满足:
整理得:
将式(15)代入式(18)可得:
在确定ki后,通过式(15)设计kc使系统达到最佳阻尼比ξopt=0.707,由此kc的表达式为:
2.2 组合型有源阻尼控制策略
如图4 所示,交流侧控制部分采用组合型有源阻尼控制,网侧电流isk(k=a,b,c)、交流侧电容电压uck(k=a,b,c)经高通滤波器和坐标变化得到d 轴的高频振荡信号,分别乘以ICF、CVF 反馈增益系数,乘积之和为阻尼电流iDamp,再由iDamp除以idc得到σac;直流侧通过配置好状态反馈系数同样可得σdc;最终将σac、σdc相加得到σd。为保持系统网侧电压电流同相位运行,需要进行功率因数修正,将修正后的开关信号经过坐标变换和空间矢量调制,得到整流桥驱动信号。
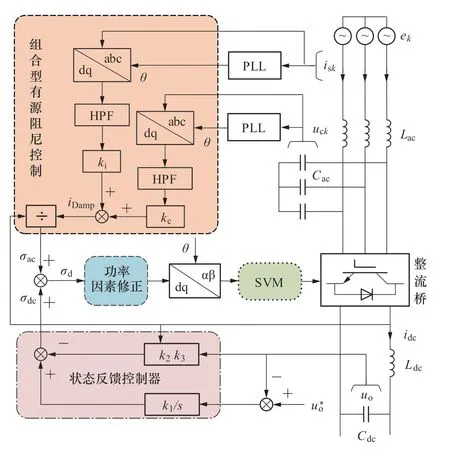
图4 CSR 控制框图Figure 4 CSR control block diagram
交流侧组合型有源阻尼控制框图如图5 所示。

图5 组合型有源阻尼控制框图Figure 5 Block diagram of a combined active damping control
为消除直流侧低频分量对交流侧影响,本文在ICF、CVF反馈增益系数前设置了高通滤波器,其传递函数如下:
其中,ωHP为高通滤波器的截止频率。
由图5 可得,交流侧传递函数为:
由式(19)计算出ki=0.44,由式(20)计算出最佳阻尼比下kc。将ki、kc代入式(23)、式(24),绘制传递函数的Bode 图和单位阶跃响应图如图6、图7 所示。

图6 Gac1、Gac2 传递函数Bode 图(一)Figure 6 Bode diagram of Gac1 and Gac2 transfer functions(No.1)

图6 Gac1、Gac2 传递函数Bode 图(二)Figure 6 Bode diagram of Gac1 and Gac2 transfer functions(No.2)
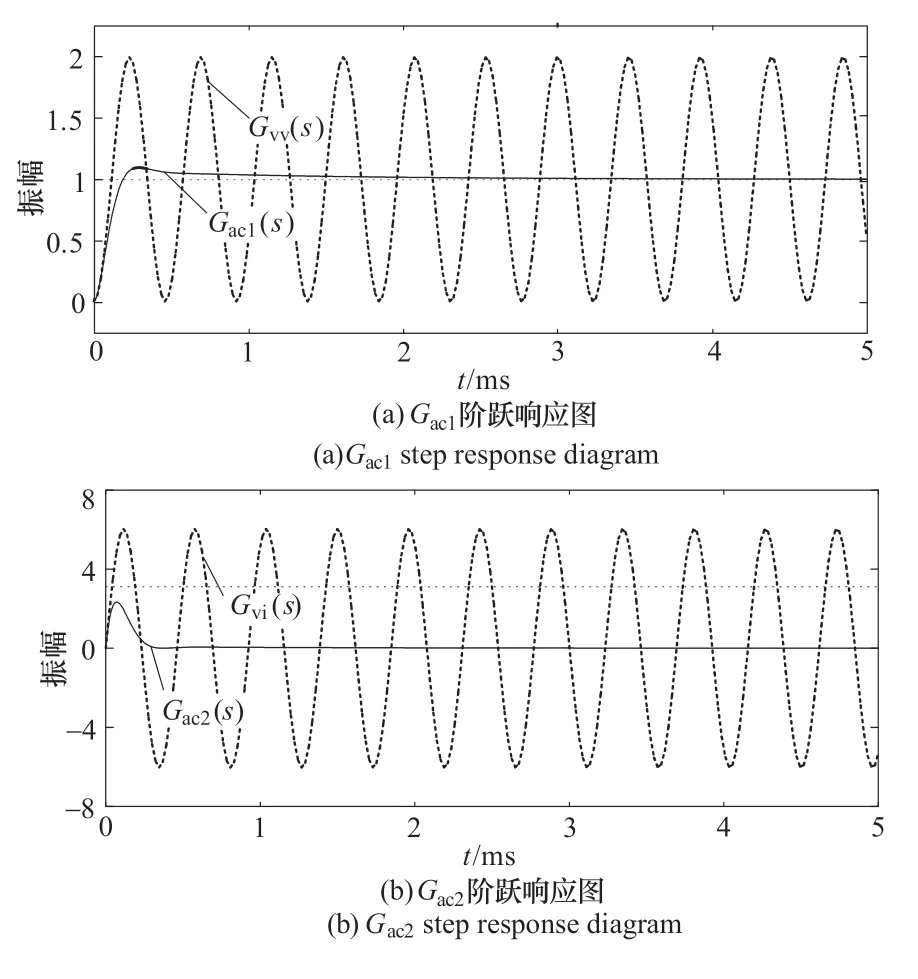
图7 Gac1、Gac2 传递函数阶跃响应图Figure 7 Step response plots of Gac1 and Gac2 transfer functions
系统网侧电压ed、整流桥输入电流id相对于交流滤波电容电压ucd的Bode 图,如图6(a)、图6(b)所示。图中传递函数Gvv(s)与Gvi(s)是指不含CVF 和ICF 时系统的传递函数。可以看出,组合型有源阻尼控制方法,能够有效抑制LC 谐振尖峰,尖峰幅值由150dB 变为0dB;此外,该方法还能减小网侧电压ed谐波和直流电流idc突变引起的交流侧电容电压ucd振荡。
系统网侧电压ed、整流桥输入电流id相对于交流侧电容电压ucd的阶跃响应图,如图7(a)、图7(b)所示。图中传递函数Gvv(s)与Gvi(s)是指不含CVF 和ICF 时系统的传递函数。组合型有源阻尼控制方法优化了系统的阻尼比,其调节时间约为0.4ms,抗干扰能力强,能较好地满足系统设计要求。
2.3 状态反馈控制器设计
直流侧采用状态反馈控制,控制框图如图8 所示。本文选定输出电压uo及直流电流idc作为状态变量,其状态反馈系数分别为k2和k3;输出电压uo经积分环节无静差跟踪输出参考电压u*o。根据控制框图建立uo与u*o的闭环传递函数:
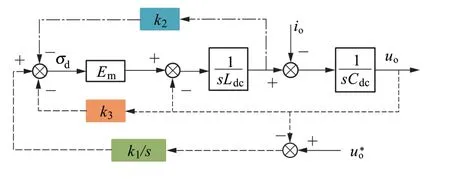
图8 状态反馈控制框图Figure 8 Diagram of the status feedback control block
其中,Em=1.5ucd。
根据图8,建立io到uo的传递函数:
式(26)为Ⅰ型系统的ITEA 标准传递函数,根据其标准形式,将状态反馈系数设置如下:
式中,ωⅠ略大于直流侧LC 滤波器谐振频率ωdc。
由传递函数式(25)、式(26)分别绘制Bode 图,如图9 所示。根据图9(a)可知,系统闭环传递函数低频段增益为0dB,所以系统输出能够实现无静差地跟踪输入指令,跟随性能良好,稳态精度高;图9(b)显示,低频段增益在-40dB范围附近,表明系统输出电压uo对输出电流io扰动具有很快的响应速度,可有效抑制输出电流扰动。
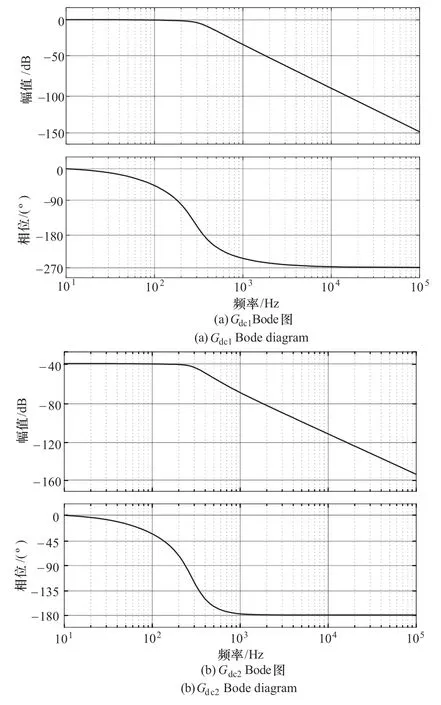
图9 Gdc1、Gdc2 传递函数Bode 图Figure 9 Bode diagram of Gdc1 and Gdc2 transfer functions
2.4 功率因数修正
系统建模过程中,由于将d 轴定向于交流侧电容电压矢量,导致系统基波位移因数不为1,需进行无功补偿使系统在单位功率因数下运行。由系统交流侧各信号矢量关系,绘制如图10 所示的矢量关系图。
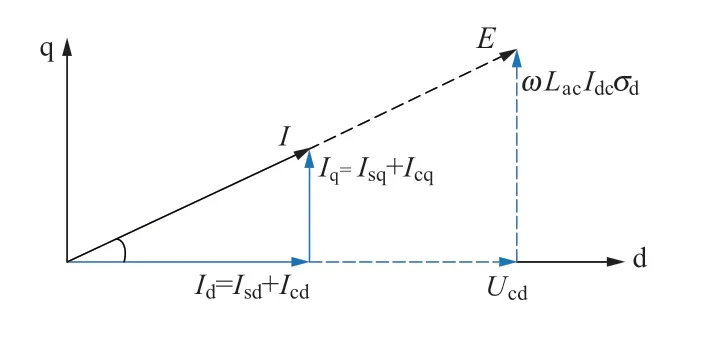
图10 交流侧相量关系图Figure 10 Diagram of phasor on the AC side
其中,d-q 坐标系下,网侧电流矢量Isd=σdIdc、Isq=σqIdc,滤波电容电流矢量Icd=0、Icq=ωCacUcd≈0。
根据三角形相似定理,可得:
由式(31)可知,当d 轴和q 轴开关函数满足此关系,即可实现I和E同相位的单位功率因数运行。
3 仿真及实验结果分析
3.1 仿真分析
利用MATLAB/Simulink 对系统进行仿真,其详细参数如表1 所示。
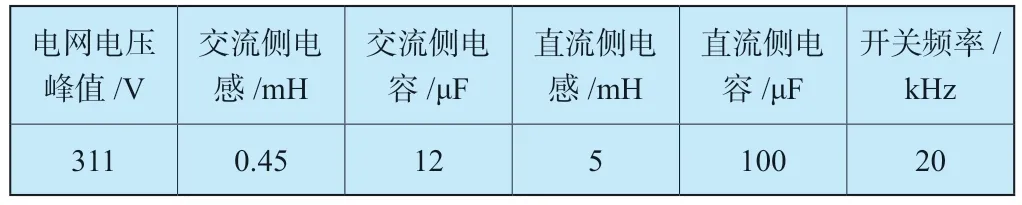
表1 CSR 系统参数Table 1 Main parameters of CSR system
系统在额定功率满载(10kW)下稳态运行仿真结果如图11(a)所示,网侧电压、网侧电流同频同相,A 相电流谐波总畸变率为1.14%,符合THD<5%的标准;输出功率半载(5kW)时,CSR 的稳态运行仿真结果如图11(b)所示,网侧电压、网侧电流同频同相,A 相电流谐波总畸变率为1.87%,符合THD<5%的标准。
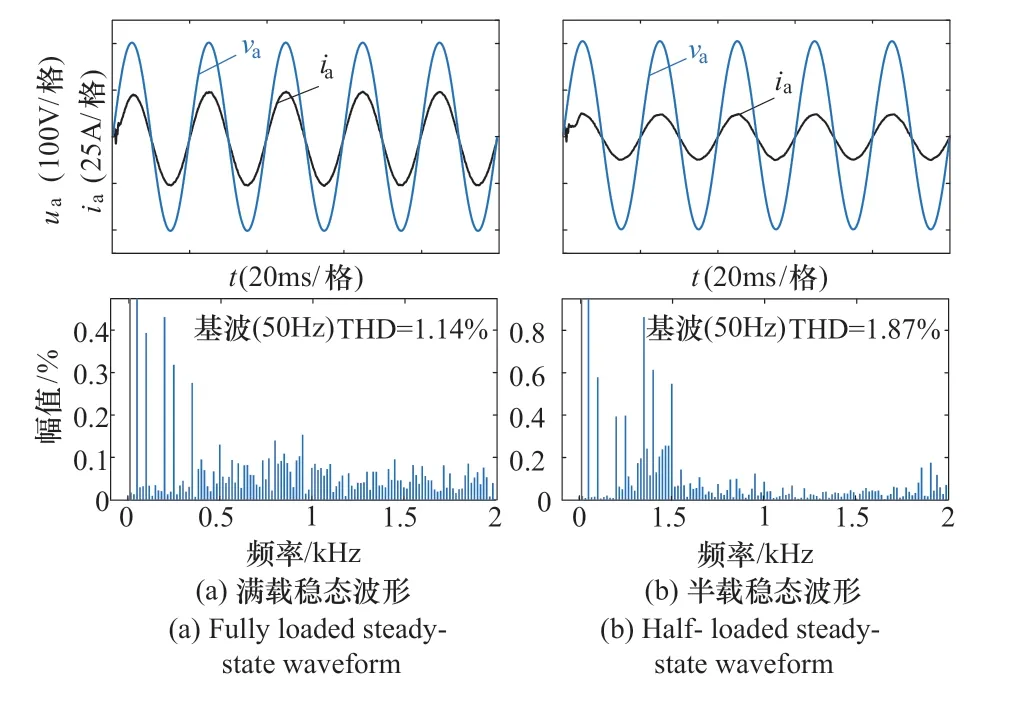
图11 满载、半载CSR 稳态运行仿真波形Figure 11 Full-load and half-load CSR steady-state operation simulation waveforms
为检验系统的动态性能,在0.1s 时将满载(10kW)负荷切换至半载(5kW)负荷情况下,CSR 系统的动态响应仿真结果如图12所示,切换负载时,系统输出电压调节时间为3~5ms。总之,仿真结果表明,CSR 在该控制策略下的稳态性能良好,负荷改变时其超调量小,响应速度快,系统动态性能好。
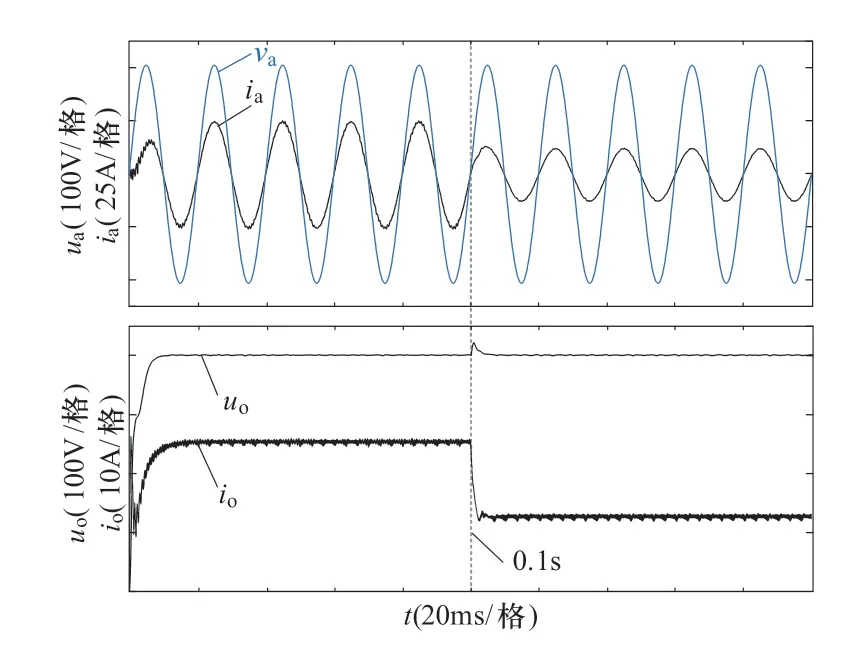
图12 变负载CSR 动态响应仿真波形Figure 12 Variable load CSR dynamic response simulation waveform
3.2 实验结果
搭建了带容性负载CSR 样机,实验参数同表1,CSR 输出功率为10kW。如图13 所示,采用基于模型的控制设计方案,利用代码生成技术,将Simulink 仿真模型生成的.c 文件导入DSP 开发板中,驱动CSR 整流。
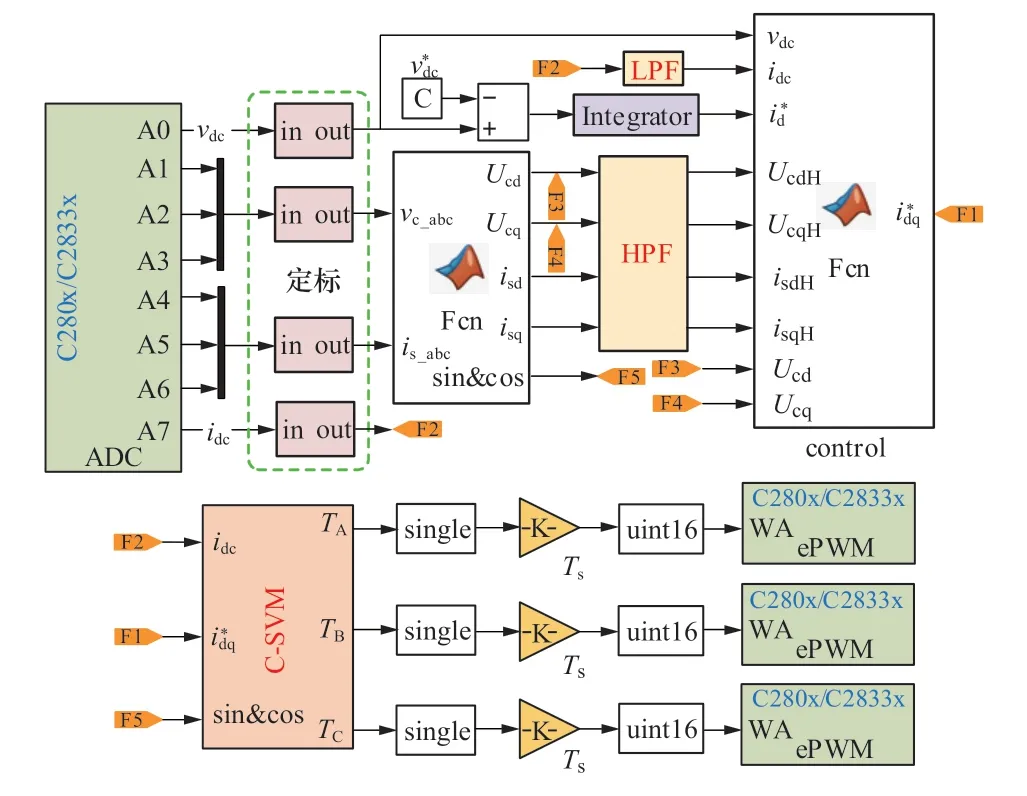
图13 基于模型的代码生成控制框图Figure 13 Model-based code generation of control block diagrams
额定输出功率情况下,网侧电压、网侧电流、输出电压、输出电流波形图如图14(a)所示。可以看出,网侧电压与网侧电流同频同相;系统输出电压能够稳定在给定值400V 且输出电流纹波小,能稳定在25A。为验证系统的动态性能,直流输出负载由满载(10kW)切换至半载(5kW),即输出电阻RL 由16Ω 切换至32Ω 时,系统的动态响应波形如图14(b)所示。当负载突变时,系统输出电压调节时间为5ms,动态响应速度快且超调量小,变负载后仍能稳定在给定输出电压400V,输出电流由25A 变为12.5A,其调节过程平滑,调节时间短,网侧电流能够在单位功率因数下正常运行。

图14 稳态、动态实验波形图Figure 14 Steady-state,dynamic experimental waveform diagram
4 结束语
本文搭建三相电流型PWM 整流器仿真模型及其实验样机,在d-q 坐标系下简化了CSR 数学模型,实现系统解耦控制。采用电容电压反馈(CVF)和电感电流反馈(ICF)的组合型有源阻尼控制,抑制交流侧LC 滤波器谐振尖峰,提高系统阻尼比及稳定性;直流侧采用状态反馈控制,使直流侧跟随给定电压稳定输出,系统的动态性能良好;最后,通过带容性负载CSR 样机实验,验证了该控制策略能使系统保持单位功率因数运行,同时网侧电流谐波含量满足电力行业标准,系统在动态运行时仍具有良好性能。
