基于任意转子位置静止时域响应试验的同步电机动态参数辨识
2024-01-12马一鸣贺儒飞彭煜民李泽泉
马一鸣,贺儒飞,彭煜民,肖 洋,李泽泉
(1.南方电网调峰调频发电有限公司储能科研院,广东省广州市 511499;2.华中科技大学电气与电子工程学院,湖北省武汉市 430074)
0 引言
同步电机的参数,特别是以各阶次瞬态电抗和时间常数为主的动态参数,决定了电机的功率输出特性与稳定运行边界,在性能考核、运行控制与保护整定等方面具有重要意义。工程上常用三相突然短路试验与电压恢复试验完成参数辨识,但此类方法不仅会造成较大的安全隐患,而且仅能辨识d 轴参数。静止频率响应(Standstill Frequency Response,SSFR)试验、静止时域响应(Standstill Time-domain Response,SSTR)试验与直流衰减法等静态方法虽然可以提高试验的安全性,但存在必须在试验前进行转子预定位的缺陷,因此,不适用于大容量机组。为提高静态试验方法的可行性,本文提出一种任意转子位置静止时域响应试验方法,通过改变常规静止时域响应试验的接线方式,实现了任意转子位置下转子位置角的确定以及电机d、q 轴全参数的辨识,并详细推导了相应的半解析化参数辨识方法。该方法的有效性通过在一台6kW 动态模拟同步电机的样机试验完成验证,并与其他参数辨识方法的试验结果进行对比分析。
1 静止时域响应试验原理
与SSFR 试验类似,SSTR 试验需要在电机处于静止状态下进行,试验接线示意图如图1 所示。试验时,首先需要将转子轴线分别置于进行d、q 轴试验的特定的位置,并将励磁绕组短路。然后,在电枢绕组两相之间施加一定形式的电压信号,并对施加信号后的电枢回路与励磁回路瞬态电流响应数据进行录波。
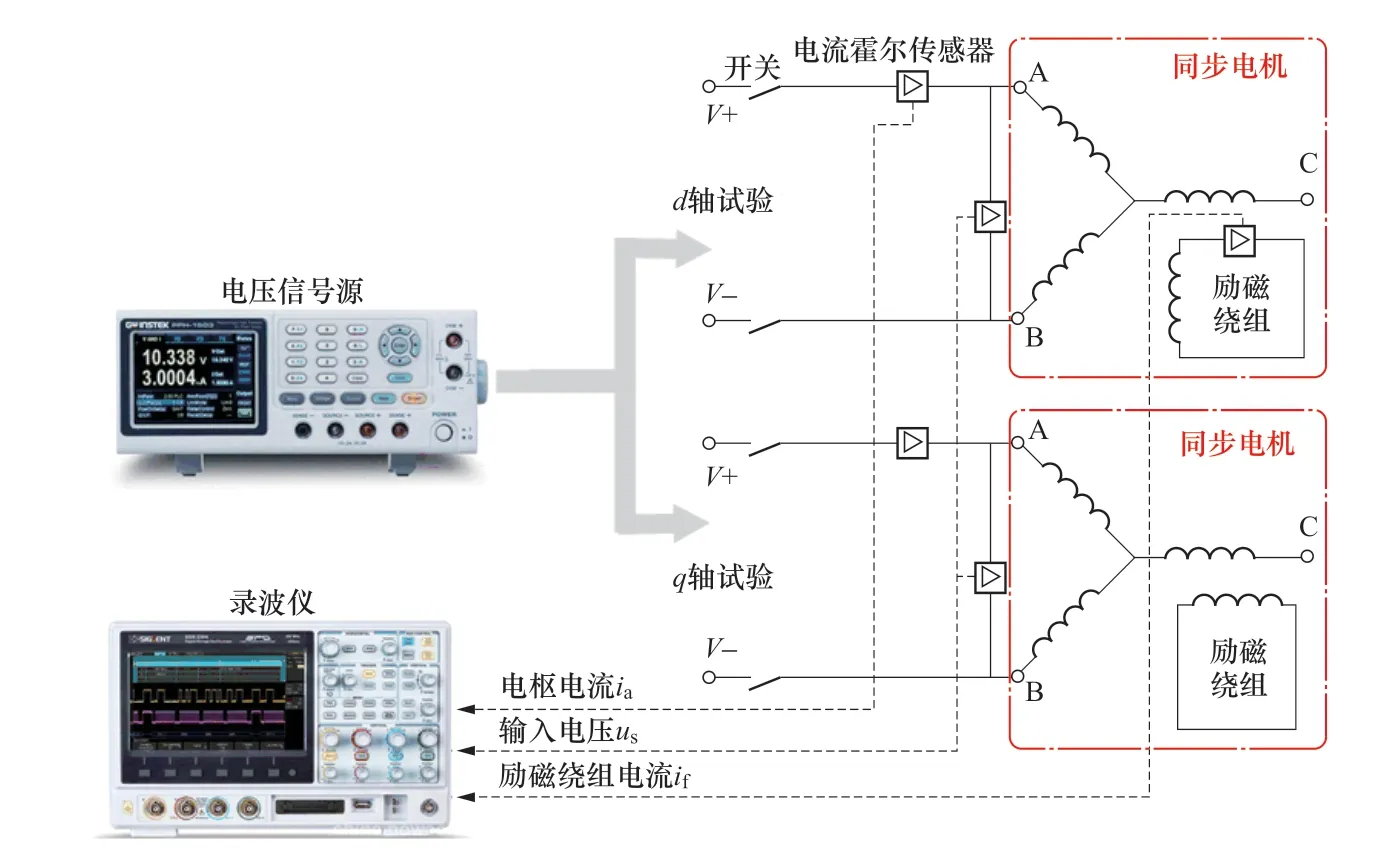
图1 常规SSTR 试验示意图Figure 1 Schematic diagram of conventional SSTR test
该试验中,电压信号的选择是多种多样的,直流阶跃电压信号[1]、sinc 电压信号[2]、脉冲电压信号[3]、chirp 电压信号[4]均已见应用[5],其中由于直流阶跃电压信号形势简单且便于获取,具备较高的工程实用价值,因此,在目前的研究中最为常用。另外,在常规的SSTR 试验中,d、q 轴动态参数需要在特定转子位置下进行辨识。SSTR 试验的转子预定位方法与IEEE 标准中给出的SSFR 试验的转子预定位方法相同,即通过在定子端施加低压交流电,并缓慢拖动转子,然后对励磁绕组的感应电压进行测量[6]。在图1 中d 轴试验所示的转子位置下,直流阶跃电压施加电枢绕组的A、B 相,此时励磁绕组轴线与C 相绕组轴线垂直,d 轴电压ud、电流id与定子电压us、电流is的幅值关系如下。当进行q 轴试验时,q 轴的电压与电流同样满足以上关系[7]。
在不同转子位置下,根据输入电压信号与瞬态电流响应性信号的关系,即可分别对d 轴与q 轴等效电路参数进行辨识,具体将在第三节中详细陈述。
2 任意转子位置下的静止时域响应方法
本文通过改变常规SSTR 试验的接线方式,提出了一种三相接法的任意转子位置SSTR 试验方法,从而省略转子的预定位过程,提高静止时域响应方法应用于大容量同步电机的适用性。本节提出的三相接法任意转子位置SSTR 试验的接线原理图如图2 所示。图中,定子绕组A 相接于信号源正端,而定子绕组B 相与C 相并联后接于信号源负端。
图2 三相接法任意转子位置SSTR 试验原理图Figure 2 Schematic diagram of SSTR test at any rotor position using three-phase connection method
在此接连方式下,定子侧三相电压满足:
进一步,对定子侧三相电压进行Park 变换可得:
由电压Park 变换的结果可知,此绕组连接方式下,在定子端施加电压信号us,等效于在d 轴方向施加电压信号2uscosθ/3,同时在q 轴方向施加电压信号2ussinθ/3。由于进行静止试验时,不存在磁路的饱和,因此可以忽略d、q 轴的耦合,从而可以将ud与uq引起的瞬态电流响应独立考虑[8]。这样,此时的d 轴电流响应相当于当转子轴线与A 相绕组轴线夹角为0°时,由电压信号uscosθ引起的纯d 轴电流响应,对q 轴可以进行类似的考虑。
根据以上分析,对录波获得的定子三相暂态响应电流进行Park 变换,获得的d 轴电流id即为当转子轴线与A 相绕组轴线重合时由uscosθ电压引起的纯d 轴暂态响应电流;Park变换得到的q 轴电流iq即为当转子轴线与A 相绕组轴线垂直时由ussinθ电压引起的纯q 轴暂态响应电流。可见,通过改变SSTR 试验的绕组连接方式,若已知转子位置角θ,由定子三相暂态响应电流的Park 变换,可以一次性获取相当于转子轴线分别对齐于d 轴试验与q 轴试验所需位置时,对应的纯d 轴暂态响应电流与纯q 轴暂态响应电流。之后,即可依据常规SSTR 试验的动态参数辨识流程对两轴动态参数进行辨识,
现需解决转子的位置角θ的获取问题,为尽可能使用与SSTR 试验相同的试验设备,本节中给出一种简便易行的辨识转子位置角的试验方法。
转子位置角确定试验的接线原理图如图3 所示,试验时,电机静止,定子三相绕组短路相连,信号源接于转子励磁绕组,从励磁绕组端口输入直流阶跃电压信号,并对定子三相暂态响应电流进行录波。由于此时仅有d 轴绕组被激励,因此,定子三相电流ia、ib与ic进行Park 变换后得到的q 轴电流iq应为0[9],也即满足:

图3 转子位置角确定试验原理图Figure 3 Schematic diagram of rotor position angle determination test
进一步,可以计算转子位置角θ为:
3 半解析化参数辨识方法
由电机暂态分析理论,在不考虑各阻尼绕组初始磁链的情况下,d 轴磁链可表示为[10]:
其中,xd(s)表示d 轴的运算电抗;Gf(s)表示励磁绕组的传递函数;id(s)与if(s)分别表示频域下的d 轴电流与励磁电流。当d 轴仅考虑一个阻尼绕组时,xd(s)与Gf(s)满足如下表达式:
其中,TDσ为d 轴阻尼绕组漏磁时间常数;rf为励磁绕组电阻;含0 的下标表示定子绕组开路状态。
由于此时电机的励磁绕组短路,则d 轴的电压方程满足:
考虑d 轴输入的电压为直流阶跃电压信号,该信号的频域表达式为:
进而,可得d 轴电流id(s)为:
根据if(s)与id(s)的传递函数,if(s)可表达如下:
由于d 轴等效电路仅存在一条阻尼回路,因此,d 轴电流id(t)与励磁绕组电流if(t)的时域通解形式为:
其中,C1、C2、C3和D1、D2、D3为各分量的幅值系数;λ1、λ2、λ3为衰减系数;id∞表示电流的稳态值。
根据时域通解形式对定子绕组电流与励磁绕组电流进行时域拟合,并将获得的id(t)与if(t)转化至频域后再整理为有理分式形式:
由式(12)、式(13)可得式(16)与式(17)的各系数为:
为求解动态参数,需要引入如下的计算辅助量:
若以时间常数的倒数为求解量,式(21)与式(22)符合一元二次方程中的韦达定理,由此可以通过构造方程法对时间常数T′d0与T″d0进行求解。当设置方程的二次项系数为1时,对应的方程如下:
进而可以解得:
类似地,可以通过C与D构造另外一个方程求解T′d与T″d:
以时间常数的求解结果为基础,可进一步得到d 轴等效电路的其他参数如下:
由以上推导过程可知,运用id(t)与if(t)的时域拟合结果,d 轴等效电路全部参数均可解。
4 试验验证与分析
本文提出的任意转子位置静止时域响应试验方法,在一台1150MW 大型核电发电机组的6kW 动态模拟电机上进行验证,同时将该试验方法得到的试验结果与常规静止时域响应试验方法及GB/T 1029 中三相突然短路法、电压恢复法等方法获取的试验结果进行对比。
动模电机的试验平台如图4 所示,该试验包括两个部分,其一是转子位置角确定试验,其二是SSTR 试验。试验时直流电压Udc= 1V,直流电源出口端串联了一个0.33Ω 的电阻,以防止定子电流过大。

图4 三相接法任意转子位置SSTR 试验平台Figure 4 Test platform for arbitrary rotor position SSTR with three-phase connection
试验在两个转子位置角下进行,分别是θ1= 45°,θ2=120°。试验中,由定子三相瞬态电流计算得到的转子位置角如图5 所示,计算结果分别为43.0°与117.9°,与给定值的相对误差分别为4.4%与1.75%。

图5 样机转子位置角确定试验位置角计算结果Figure 5 Calculation results of rotor position angle determination test
辨识位置角后,即可对两位置角下获得的三相瞬态电流响应进行Park 变换,从而进行时域拟合和动态参数辨识。d轴电流与q 轴电流的时域通解形式可以表示为:
其中,α和γ表示电流衰减分量的幅值系数,β和η表示衰减系数;id∞与iq∞分别表示d 轴与q 轴的稳态电流。
图6 显示了不同位置角下去噪后的d、q 轴电流及其时域拟合结果,下标1 与2 分别对应于转子位置角θ1与θ2下进行的试验。

图6 两转子位置下d、q 轴电流响应及其时域拟合结果Figure 6 Current response and time-domain fitting results of d- and q-axis at two rotor positions
表1 给出了时域拟合中各系数的具体结果。

表1 时域拟合结果Table 1 Time-domain curve fitting result
根据时域拟合结果,可对动模电机d、q 轴各阶暂态电抗与暂态时间常数进行计算,动态参数辨识值与优化值的对比结果如表2 所示,作为对比,该样机在转子位置角θ1下进行的两相接法任意转子SSTR 试验的辨识结果也显示在表中。为验证三相接法任意转子位置SSTR 试验的动态辨识结果,对动模电机开展了GB/T 1029 中给出的三相突然短路试验及其他型式试验以进行动态参数辨识,三相突然短路试验中端电压值为0.3 倍的额定电压以确保获得动态参数为不饱和值。另外,q 轴同步电抗由低转差法获得,为不饱和值;q 轴次暂态电抗由静测法获得,同样为不饱和值;由于不方便抽出转子测量定子漏抗,定子漏抗xsl由短路特性试验结果计算得到的保梯电抗xp来代替,由于动模电机属于隐极式同步电机,xp与xsl相近,xp略大于xsl;通过以上国标推荐的试验方法获得的参数在表2 最后一列给出。
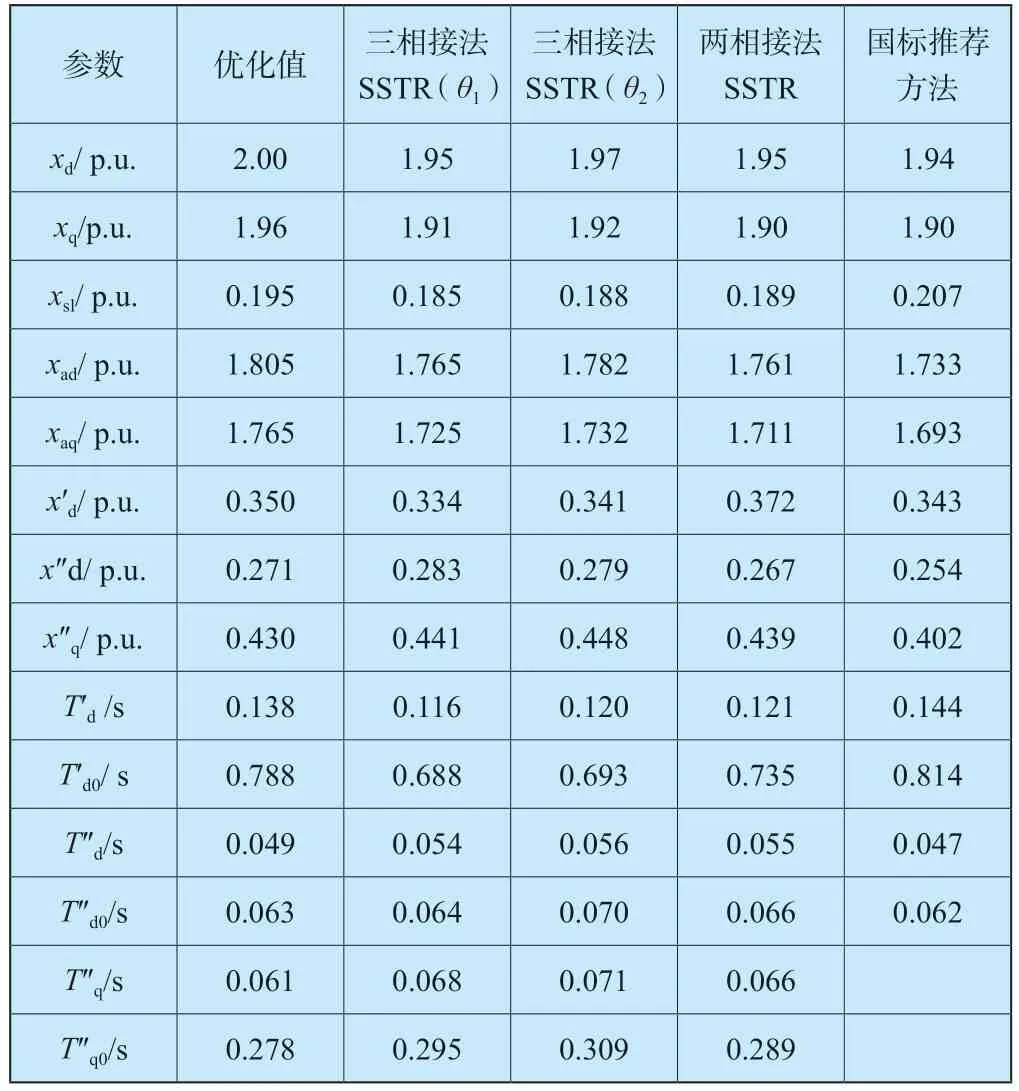
表2 动态参数辨识结果对比Table 2 Comparison of dynamic parameter identification result
如表2 所示,通过多个试验的实测结果,样机的动态参数与动模电机的动态参数设计目标值吻合良好,各实测值与动态参数优化值的最大误差仅在10%左右,证明了动模电机优化方案的正确性。其中,在暂态时间常数上存在一定误差,这主要是因为试验时需要将励磁绕组短接,导线引入了新的电阻,使时间常数变小,三次SSTR 试验的辨识结果可验证这一结论。此外,通过三相接法任意转子位置SSTR 试验辨识得到的动模电机动态参数与通过两相接法任意转子位置SSTR 试验和国标推荐方法获得的动态参数均能够良好匹配,即便在最难准确辨识的次暂态参数上,相对误差也不超过17%,这证明了该试验方法的有效性。
5 结论
本文提出了一种任意转子位置下的静止时域响应试验方法及其参数辨识方法,通过修改常规静止时域响应试验的接线方式,由一次试验的三相瞬态响应电流的Park 变换计算出纯d 轴与纯q 轴响应电流,并给出了一种简便的辨识转子位置角的试验方法。在确定转子位置角后,利用单次试验的结果即可半解析化辨识出d 轴与q 轴全部的动态参数,不仅能够降低试验难度,省略常规静止时域响应试验必需的转子预定位过程,而且可以提高辨识效率,减少定位误差对辨识结果的影响。本文的试验方法在一台6kW 的动态模拟同步电机上完成验证,能够达到与GB/T 1029 中推荐方法与常规静止时域响应试验方法相同的辨识精度,证明了本方法的有效性与先进性。
