基于双层多情景的风光抽水蓄能混合系统多目标随机优化研究
2024-01-12刘杰杰孟现阳吴江涛
刘杰杰,李 尧,孟现阳,吴江涛
(西安交通大学热流科学与工程教育部重点实验室,陕西省西安市 710049)
0 引言
为应对全球能源危机和环境破坏等问题,近年来,世界各国都在努力进行能源转型,发展清洁能源,倡导低碳经济[1-4]。我国也于2020 年提出了“碳达峰、碳中和”这一项国家重大发展战略,电力行业是实现可持续发展目标的关键。2022 年,能源电力行业碳排放占全国碳排总量59.4%[5]。提高可再生能源的渗透率已成为电力系统转型的重要路径之一[6-8]。青海省“富光丰水风好地广”的天然能源资源优势,为其发展清洁能源奠定了坚实的基础。然而,随着风光等新能源大规模并网,其间歇性、波动性使得弃风弃光及电网调峰等问题十分突出,严重制约了清洁能源的高效利用。作为较成熟抽水蓄能技术,不仅可以改善可再生能源并网带来的不稳定性,而且也促进了最大程度消纳风光等清洁资源。基于此将风光可再生能源和抽水蓄能技术结合,是实现风光消纳和电网稳定运行的有效途径[9-12]。
现有的风光储能源系统优化研究,主要从容量规划和运行调度两个方面开展研究。张良等[13]基于灰狼算法建立了风-光-抽水蓄能混合系统的多目标优化模型。段佳南等[14]采用出力期望函数来描述多个风、光发电利益主体聚合后出力的随机性,并提出了基于合作博弈理论的风、光、水、氢多主体能源系统增量效益(增益)分配策略。Xu 等人[15]以四川省光伏-风电场-抽水蓄能装置混合能源系统为例,采用多目标粒子群优化算法实现了供电可靠性最大、投资成本最小的最优配置。Zhou 等人[16]提出了一种基于并网水风太阳能资源结合灵活储备的多目标调度模型,以协同保证极端干热天气下远距离输电和局部电力需求的供电可靠性。
上述文献通常在典型年工况下进行建模规划,而混合系统由多个设备组成。其相互作用和融合使系统设计变得复杂,特别是环境参数和用户负荷一直在变化,这给供需匹配优化带来了巨大挑战。而性能优异的系统应保持高可靠性,并能适应运行中的多种不确定性。因此,亟须建立一套合理的方法实现混合动力系统不确定条件下容量和运行协同优化。
1 系统介绍
1.1 风光抽水蓄能系统
本研究基于位于青海省尖扎县和化隆县交界的黄河干流李家峡的实际工程项目为背景,分析了光伏-风电-抽水蓄能混合可再生能源系统的应用潜力。图1 给出了混合系统的示意图。如图1 所示,系统包括风力发电机组、光伏发电机组、抽水蓄能机组和用户需求侧。当风机和光伏的总发电量大于当地电网实时需求时,启动抽水泵机组,将多余的电力存储进水库;反之,当光伏和风机的发电量不足以满足电网需求时,抽水蓄能系统释能,作为补充电源。
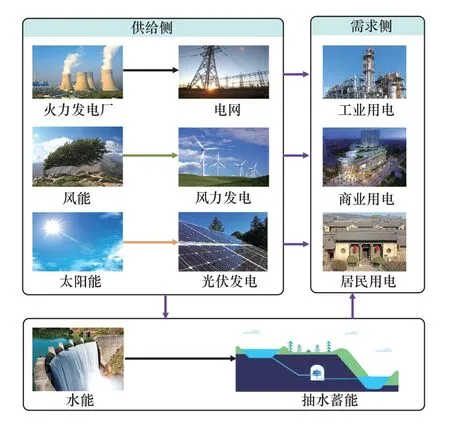
图1 系统图Figure 1 The diagram of hybrid system
1.2 设备热力学模型
光伏的发电量可以表示为:
式中:Npv——光伏的实际装机容量,MW;
Gact——实际太阳辐射强度,kW/m2;
Gsta——光伏板标准测试条件下的太阳辐射强度,kW/m2;
ω——温度系数,%/℃;
Tact——大气环境温度,℃;
Tsta——标准测试条件下环境温度,℃。
风机的发电量可以表示为:
式中:Nwind——风机的实际装机容量,MW;
v——环境风速,m/s;
Vin——风机的切入风速,m/s;
Vsta——风机的额定风速,m/s;
Vout——风机的切出风速,m/s。
由于风机的轴心高度与地面高度差较大,用地面的环境风速代替风机轴心风速会产生较大误差,因而,风机轴心风速可进一步表示为:
式中:v0——地面测风站测量风速,m/s;
h——风机轴心距地面的高度,m;
h0——测风站据地面高度,m;
γ——转换系数,通常取0.143。
上游水库的水量动态变化模型可以如下表示。
抽水蓄能的充能、释能以及蓄能量约束可以表示为:
式中:Capes——抽水蓄能的容量,MW;
δes,cha——抽水蓄能最大充能速率;
δes,dis——抽水蓄能最大放能速率;
Wes——抽水蓄能的储能量,MW;
Wes,min——抽水蓄能的最小储能量,MW;
Wes,max——抽水蓄能的最大储能量,MW。
抽水蓄能的充放能状态可以表示为:
ηes——抽水蓄能自损率;
ηes,c、ηes,d——蓄电池充放能效率。
2 双层随机优化框架
两层多情景优化框架首先采用核密度估计法拟合日照强度,风速与电力负荷的概率密度,然后利用拉丁超立方抽样与K-均值生成随机场景集。随后的,在此基础上,建立两层多目标优化模型。混合优化模型包括系统配置优化(第一阶段)和运行优化(第二阶段)。前者旨在获得最优的设备类型和容量(数量)。得到的容量结果作为第二阶段的约束条件,然后进行系统的优化运行。
2.1 随机多情景生成框架
2.1.1 核密度估计
核密度估计法是数据集的概率密度的非参数估计方法中最常用的一种,其目的是直接从数据中估计未知概率密度,而无须对参数分布的分布形状做任何事先假设。根据n个观测到的数据点,对未知密度的估计如下
为了建立估计核密度,研究人员必须确定核函数。高斯核函数是一种广泛使用的概率分布,并产生以下概率密度函数:
2.1.2 拉丁超立方抽样
拉丁超立方抽样是一种随机抽样的方法,相比于蒙特卡诺抽样避免了抽样样本过度聚集的问题。其将变量范围划分成许多等距区间,并在每个小区间[i/l,(i+1)/l]内产生一个概率值Pi。打乱各个等距区间概率值的顺序,按照概率分布函数的反函数得到每个概率值对应的样本值。
2.1.3 K-均值聚类
K-均值聚类本质上是一种基于欧式距离度量的数据划分方法,其主要是来计算数据聚集的算法,主要通过不断地取离种子点最近均值的算法。首先从数据中选择k个对象作为初始聚类中心;再计算每个聚类对象到聚类中心的距离来划分;再次计算每个聚类中心;进一步计算标准测度函数,直到达到最大迭代次数,则停止,否则,继续操作。最后,确定最优的聚类中心。
2.2 两层多目标随机优化
两层混合优化方法分为第一层容量优化和第二层操作优化。对于第一层优化,以能源,经济,环境为多目标,通过创建、评估和修改装机容量来实现最佳性能。第一层优化模型的目的是寻找每个设备的最优容量。多目标函数包括三个方面:一次节能率(PESR)、年总成本节约率(ATCSR)和二氧化碳减排率(CDERR)。对于第二层优化,以小时操作成本为目标函数,优化固定容量下不同场景设备出力。
式中:F——燃料消耗量,MW;
AC——年均总成本,万元;
CD——二氧化碳排放量,万t;
Ref、IES——参考系统和混合系统。
在本文中,两层优化包括多目标优化(第一层)和数学规划(第二层)。对于多目标优化模型,找到合适的求解方法是关键的一步。通过模拟自然现象或过程的启发式算法被广泛用于解决优化问题。在众多的启发式算法中,NSGA-Ⅱ算法结合父方案和子方案生成下一个子代种群,降低了计算复杂度。精英策略用于保留种群中的优秀个体,交叉和突变使精英策略避免陷入局部最优。因此,为了对系统的能效、经济和环境性能进行综合优化,采用NSGA-Ⅱ求解第一层的多目标优化模型。在第二层优化中,由于设备的非线性特性,存在非线性约束。Gurobi 求解器中的数学算法是求解非线性问题的有效方法,求解速度快。因此,采用精确的数学算法,利用Gurobi 求解器求解第二层优化模型。在运行优化中,分别收集和更新每小时的能量需求和储能状态。以最小的运行成本为目标函数,求得各部件的输出。然后根据前一小时的运行结果更新下一小时内的储能状态。每小时进行一次优化,直到场景集结束,示意图如图2 所示。

图2 双层优化示意图Figure 2 The diagram of two-layer optimization
3 结果与讨论
3.1 基础数据
青海省尖扎县的年度逐时环境温度、风速以及太阳日照强度等环境参数如图3 所示。负荷如图4 所示。本文所涉及设备的技术参数如表1 所示。NSGA-Ⅱ算法的输入参数和决策变量的搜索范围如表2 所示。

图3 年度逐时环境参数(一)Figure 3 Annual hourly environment parameters(No.1)
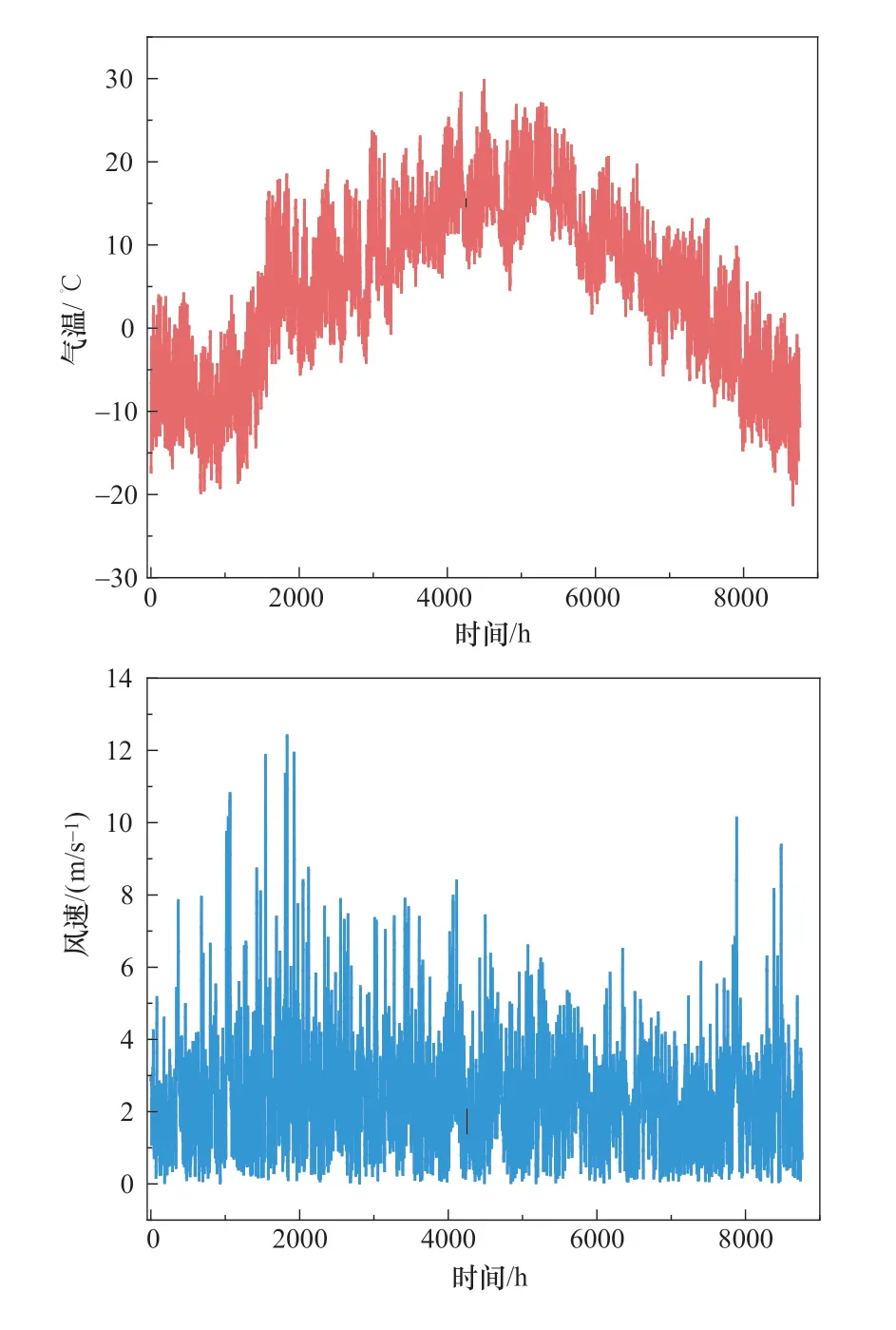
图3 年度逐时环境参数(二)Figure 3 Annual hourly environment parameters(No.2)
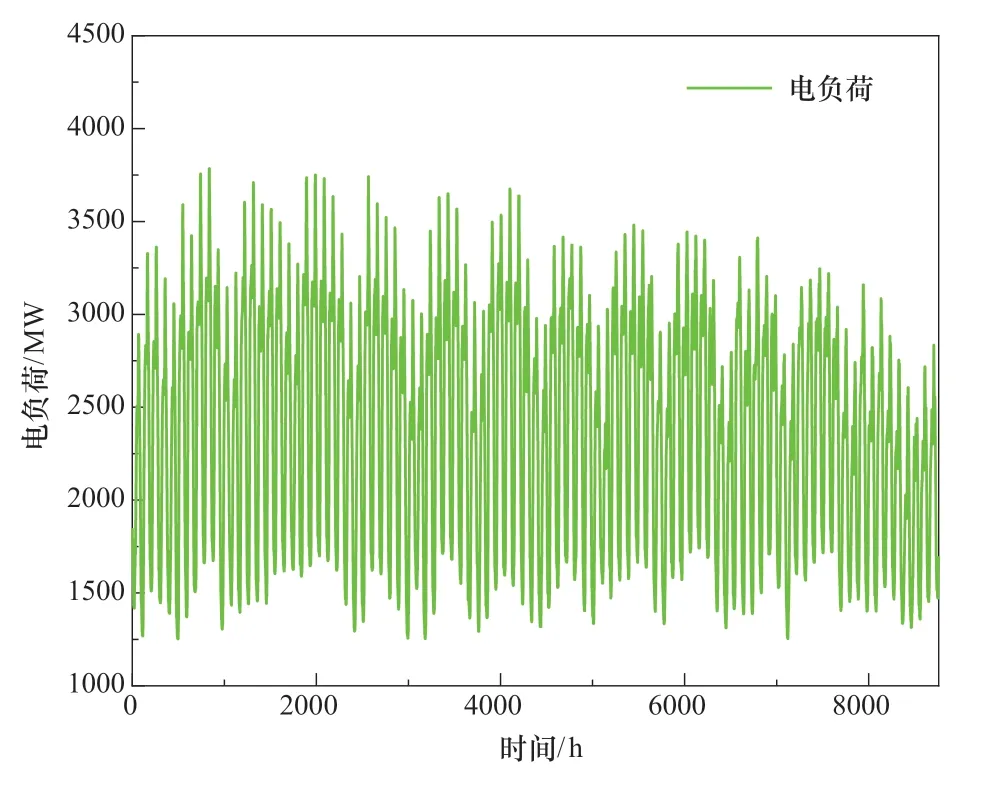
图4 年度逐时负荷Figure 4 Annual hourlyloads
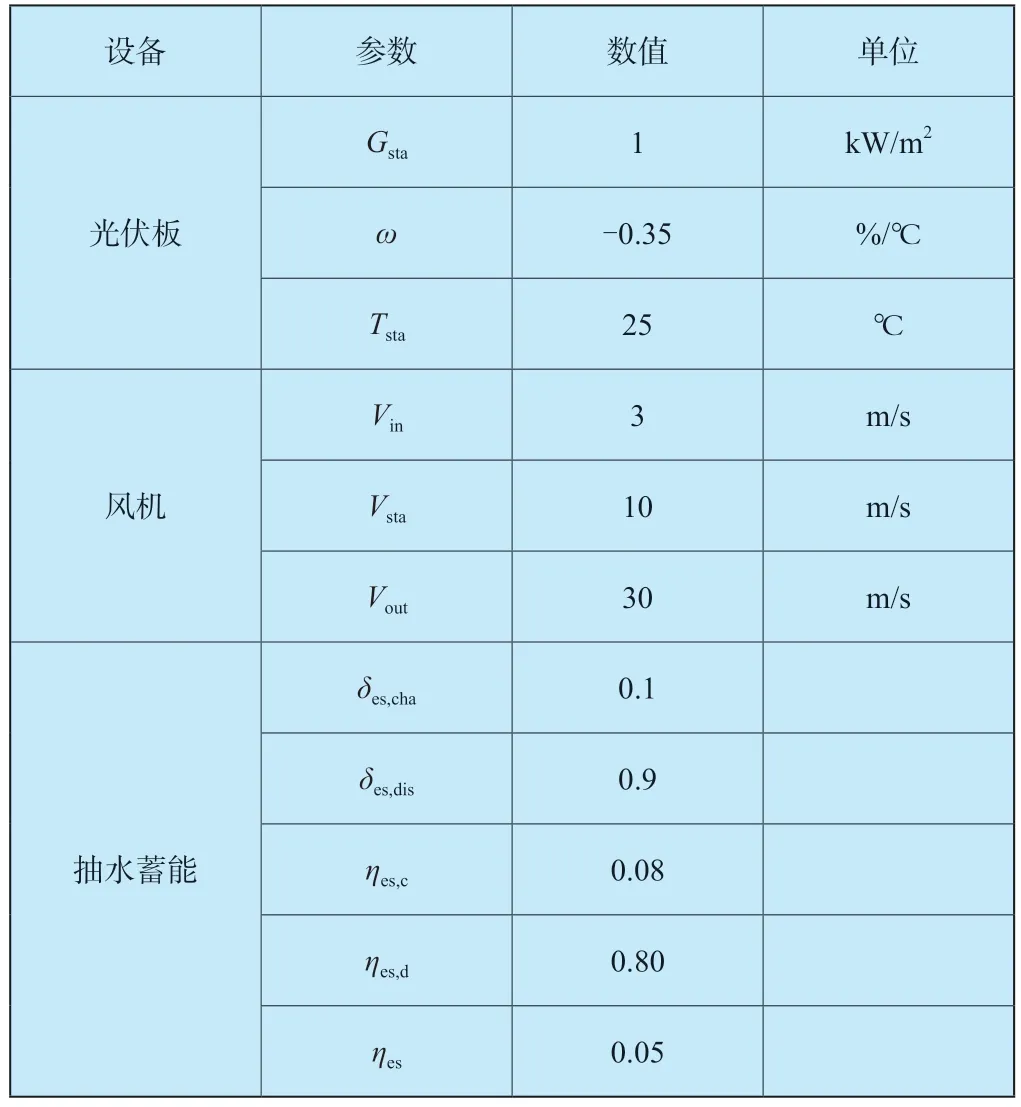
表1 设备的技术参数Table 1 The technical parameters of the equipment
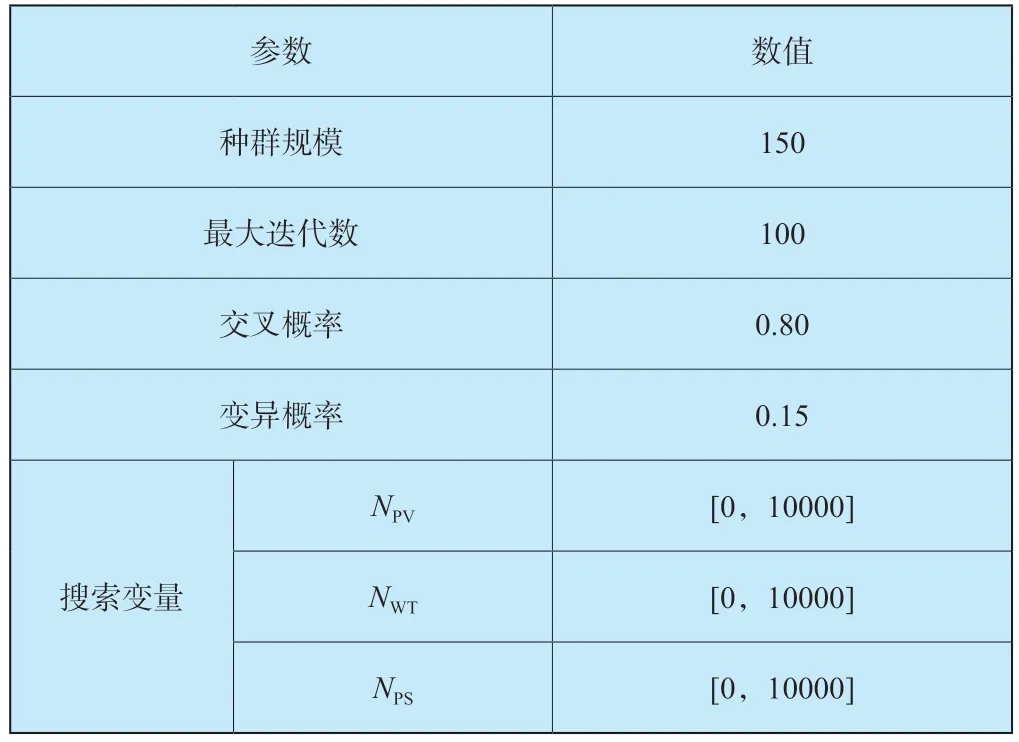
表2 算法参数Table 2 Algorithm parameters
3.2 优化结果
图5 为混合系统通过多目标优化算法NSGA-Ⅱ优化后下,系统能源、经济和环境性能的对比结果。可以看出,随着一次能源节约率和二氧化碳减排率逐渐增加,年均成本节约率呈现出减少态势;相反,混合系统随着一次能源节约率增加,其二氧化碳排放量逐渐减少,说明混合系统的环境收益十分显著。由图5 可以看出混合系统的经济收益和环境收益呈现出相反的变化规律。因此,综合考虑系统经济性以及环境收益,选取图5 中最优解点,为此多目标优化Pareto 前沿的最优解。所到的容量配置优化结果如表3 所示,混合系统一次能源节约率为61.8%,年均成本节约率为49.9%,二氧化碳减排率为61.8%。可以看出,混合系统配备大量的风机和光伏,用以满足当地巨大的电负荷需求,说明可再生能源与系统耦合度较好,从而使得系统的整体性能提升。

图5 多目标优化Pareto 前沿解Figure 5 Pareto result of multiple objectives optimization

表3 容量配置优化结果Table 3 Optimization result of capacity allocation
为了进一步展示混合系统的各组件在此容量配置下的运行状态,选取了夏季典型日进行分析,如图6 所示。从电平衡可以看出,风机在全天始终保持着较高的出力,而光伏在白天出力较高,尤其是11:00 ~15:00 时间段;电网主要在夜间保持出力,用于弥补夜间光伏出力的缺失。当系统组件出力超过电负荷需求时,多余的电力存储在抽水蓄能装置中,如15 :00 ~19 :00 时间段。当系统组件出力不足电负荷需求时,抽水蓄能释能来满足电力需求,如20:00 ~23:00 时间段。
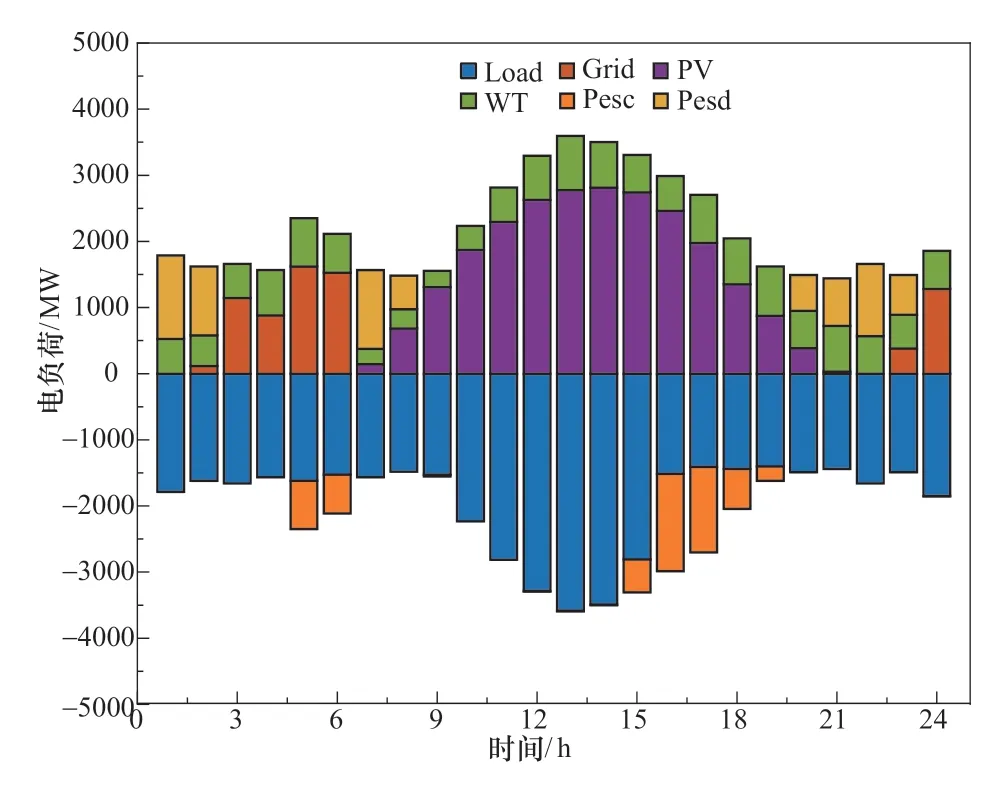
图6 混合系统典型日电平衡Figure 6 Electricity balance of typical day for hybrid system
4 结论
本文针对青海省李家峡风光水可再生能源综合应用场景,提出了一种耦合风能、太阳能以及储能模块的高比例可再生能源系统,采用双层多场景随机优化模型,以一次能源节约率、年均成本节约率以及二氧化碳减排率作为目标函数,对混合系统经济、技术以及环境性能进行了优化分析,得到了混合系统的最优容量配置和运行策略,得出了如下结论:通过对案例分析,证明混合系统拥有较好的经济和环境性能。随着一次能源节约率逐渐增加,二氧化碳减排率也逐渐增加,而年均成本节约率逐渐减少。综合考虑系统经济性以及环境收益,选取多目标优化Pareto 前沿的最优解,可以实现混合系统一次能源节约率为61.8%,年均成本节约率为49.9%,二氧化碳减排率为61.8%。
