基于改进TCNN算法的电子组装路径优化研究
2024-01-12夏威
夏威
(惠州市技师学院, 电子工程系, 广东, 惠州 516000)
0 引言
在此背景下,作为集群路由器的主要组件,通信背板上的电子元器件的数量急剧增加,组装路径也越来越复杂,通讯背板的电子器件组装的效率和质量也受到了业内人士的广泛关注[1-2]。
许頔等[3]探讨了PEDOT的制备及改进方法,并研究了改进PEDOT在电子器件组装中的应用效果。Robert van der Zwan等[4]讨论了印刷电路板中电子元器件的作用,以及电子元器件的未来发展趋势。崔译文等[5]结合改进的Hough圆检测算法和SURF算法,提出一种电子元器件的质量检测方法,实验证明该方法的特征点匹配率超过80%。
通过上述内容可知,目前对电子器件组装的相关研究更关注组装质量,忽视了组装效率。为此,研究采用暂态混沌神经网络算法(TCNN)来求解电子组装中的大规模优化问题,并针对TCNN精度低,易陷入局部最优的缺陷,采用分治策略对算法进行改进,期望能够有效缩短电子组装路径,进而提升大规模电子组装的生产效率。
1 TCNN算法的构建与优化
1.1 TCNN算法的构建与更新方式选择
通信背板的大规模电子组装路径优化问题与旅行商问题类似,均是在多个点之间寻找一条最优路径,因此研究采用旅行商问题数学模型来对电子组装路径优化问题进行描述[6-7]。电子组装路径优化本质上是最小化组合优化问题:若存在N个电子元器件C={c1,c2,…,cN},电子元器件的遍历路径表示为S={s1,s2,…,sN}。电子组装路径优化的数学模型就是在满足目标函数的前提下,通过计算获取到一个最优路径S。目标函数的表达式如式(1)所示。
(1)
式(1)中,d(ci,ci+1)表示电子元器件集合中第i个电子元器件和第j个电子元器件之间的权重。在实际生产工作中,一般采用近似算法来求解电子组装路径优化问题。目前,在电子组装路径优化问题中,蚁群算法(ACO)的应用较为广泛。但蚁群算法的求解速度较低,已逐渐无法满足规模越来越大的电子组装路径优化问题求解需求[8-9]。因此研究将Hopfield 神经网络算法(HNN)与混沌神经网络相结合,构建TCNN算法,并将TCNN应用到大规模电子组装路径优化问题求解中。混沌神经网络可用式(2)进行描述。

(2)
式(2)中,i表示第i个神经元,vi表示第i个神经元的输出,ui表示该神经元的内部状态,wij表示2个神经元i和j的连接权值,Ii表示该神经元的输入偏置,α表示一个输入缩放参数,k表示神经元阻尼因子,且有0≤k≤1,zi表示一个自反馈连接权值,且有zi>0,ε表示输出方程的步进参数,且有ε>0。基于HNN算法的能量函数,结合混沌算法,提出新的能量式,如式(3)所示。
(3)
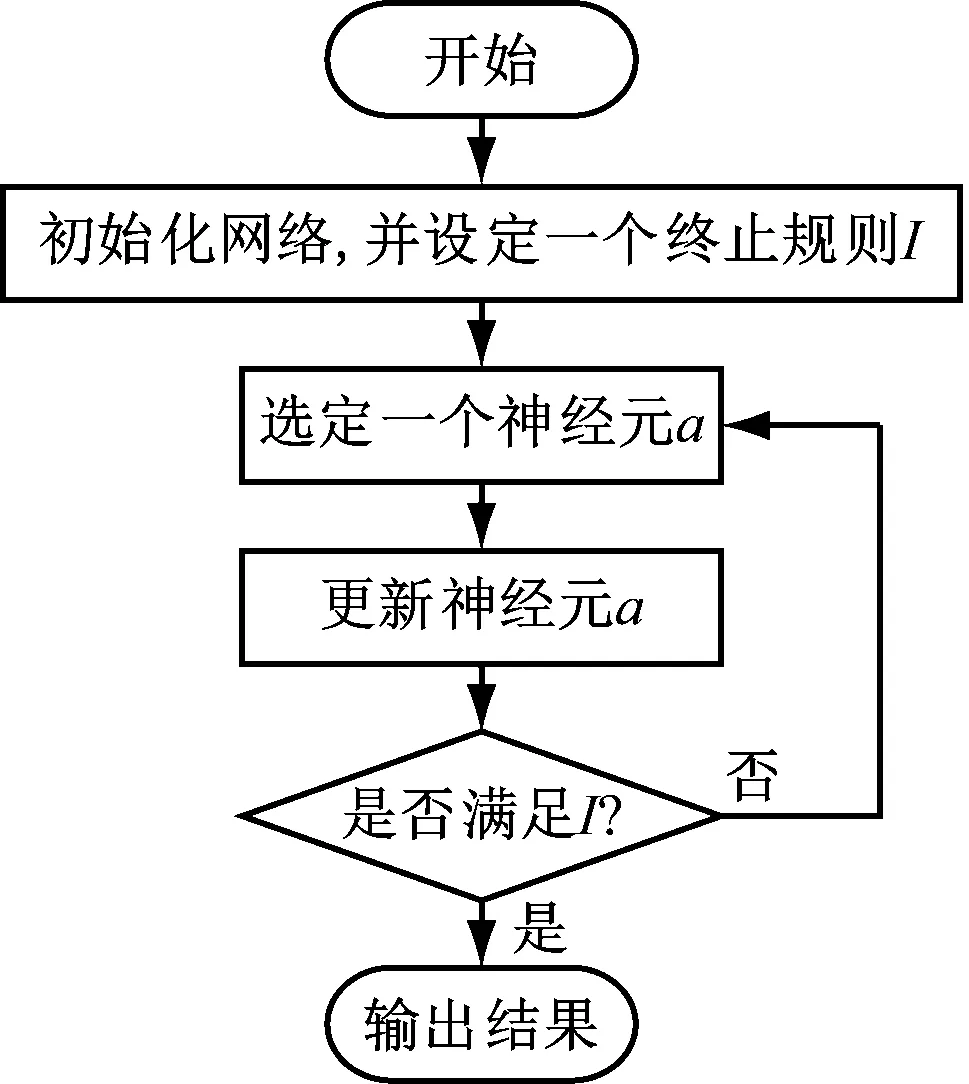
式(3)中,W1表示电子组装路径优化问题的约束条件参数,W2表示最小化路径的长度参数,dik表示电子元器件i和电子元器件k之间的距离。与原有的能量函数公式相比较,式(3)的动力学特性更为丰富,并且能够同时满足电子组装路径优化问题的约束条件以及最小化路径长度准则。电子组装路径优化问题的约束条件与旅行商问题的约束条件类似,是指:在电子元器件的组装过程中,每一次只能在一个点组装一个电子元器件,并且每个点只能组装一个电子元器件[10]。基于上述内容,即可联合HNN算法和混沌神经网络构建TCNN算法。TCNN算法的更新方式主要有2种,即异步更新与同步更新,如图1所示。
(a) 异步更新流程
在图1(a)中可知,异步更新在算法的每次更新迭代时均只更新一个神经元a的状态,其余的神经元则保持原有状态。该方法的更新速度较慢,适用于迭代次数少、规模小的神经网络使用场景。同步更新则在每次更新时都会更新所有神经元,单次更新时间会长于异步更新方式,但总迭代次数和时间会远少于异步更新,更适用于大规模的神经网络使用场景。基于通信背板的大规模电子组装路径优化问题规模大的特点,研究选择同步更新方式。
1.2 并行化策略与分治策略下的TCNN算法改进
相比ACO算法,TCNN算法的求解速度更快,求解时间需求更少,能够极大地节约时间[11-12]。但TCNN算法求解精度与传统的求解算法相比却很低,无法满足需求[13-14]。因此,研究对TCNN算法进行并行化改进,使其兼具求解精度和求解效率。GPU设备能够对矩阵运算进行提速,因此将能量函数的更新迭代方式优化为矩阵运算,再通过GPU设备进行加速,能量函数的矩阵运算模式如式(4)所示。
U=kU-z(V-I0E)+α{-W1(VM+MV)-
W2(DVN)+W1E}
(4)
式(4)中,V表示输出神经元矩阵,U表示一个能够描述神经元内部状态的矩阵,D表示距离矩阵和距离居住的对角线矩阵之差。通过TCNN算法的矩阵运算模型,就能够使TCNN算法在GPU设备上运行,并借助GPU设备实现所有神经元的快速同步更新,进一步提升TCNN算法的求解速度[15]。在大规模的求解问题中,常用分治策略将待求解问题分成多个小规模问题,并依次求解并还原,最终实现对大规模问题的求解。分治策略的原理如图2所示。

图2 分治策略的原理
研究采用分治策略来对TCNN算法进行改进,主要有4个步骤。首先对表示电路板上所有安装节点的数据集进行分割操作,将其划分为n个小规模的子集,即在电路板上将组装节点分割成n个包含了若干组装节点的区域。分割操作则借助凝聚式层次聚类方法来实现。其次,利用TCNN算法求得所有子集的最短路径,即n个区域中组装节点的最短组装路径。然后将所有子集均作为一个节点,将所有节点视作一个新的数据集,并采用TCNN算法求解该数据集的最短路径,获取所有子集的排列顺序。最后则是选择一个连接策略,将所有节点按顺序连接,从而得到初始问题的最优解。也就是说,将电路板上的所有电子器件组装节点分割成若干区域,在这些区域内求得电子组装的最优路径,再将这些区域整体视为一个组装节点,最终在整个电路板上求解最优路径。电子组装路径优化问题数据集的拆分,本质上是依据空间距离分布划分节点,因此采用层次聚类方法来将距离相近的节点划分为一个子集。当数据集规模变大时,层次聚类算法的运行时间会呈指数上升,为此,研究采用Tensorflow来寻找距离矩阵的最小值,快速划分子集,极大地缩短子集划分时间。聚类数目,即划分子集的数量,直接影响到大规模旅行商问题的求解效果。为了确定最佳聚类数目,提高算法的求解精度,研究采用TSPLIB数据集进行相关实验,对不同聚类数目下TCNN算法的求解精度进行验证。算法的求解精度用表现率指标来评估,表现率的计算方式如式(5)所示。
(5)
式(5)中,R表示表现率,L′表示所求解数据集的已知最优路径长度,L表示TCNN算法求解的该数据集的路径长度。实验结果表明,在大规模问题、中等规模问题以及小规模问题的数据集中,最佳聚类数目均为20,如图3所示。

(a) 小规模数据
因此,在通信背板的大规模电子组装路径优化问题中,均将子集数量分割成20个。利用基于GPU设备的TCNN算法对子集内部路径进行优化求解。为更好地处理大规模路径优化问题,研究采取将所有内存应用到同一个子集的优化上的策略,即对每个子集依次进行优化计算。对子集内部路径进行优化后,还需要对子集之间的路径进行优化。求得所有子集的开口端的两个点的中点,该点即表示该点所在的数据子集。用所有的子集的中点构建一个新的数据集,并利用TCNN算法对新数据集进行求解,最终得到所有子集的最终排列顺序。综合上述内容,即可完成对TCNN算法的优化和改进,进而实现电子组装路径优化,提高大规模电子组装效率。
2 改进TCNN算法的性能分析
为验证改进TCNN算法的优化效果,以及改进TCNN在通信背板的大规模电子组装路径优化问题中的求解效果,研究对其进行仿真实验。实验数据来源为5家PCB板生产厂商,实验数据的获取方法为数据挖掘,最终获取5个电子器件组装路径的数据集,分别记为数据集1、数据集2、数据集3以及数据集4、数据集5。首先验证并行化TCNN算法的性能提升效果。采用Windows 10系统运行程序,Python语言实现。GPU设备采用英伟达1050Ti,运行内存为4 GB。采用相同的数据集对优化前后的TCNN算法进行测试。并行化改进TCNN算法测试两次,第一次在CPU上运行,第二次则是在GPU上运行。两种算法对各个数据集求解所需的时间,以及表现率如表1所示。
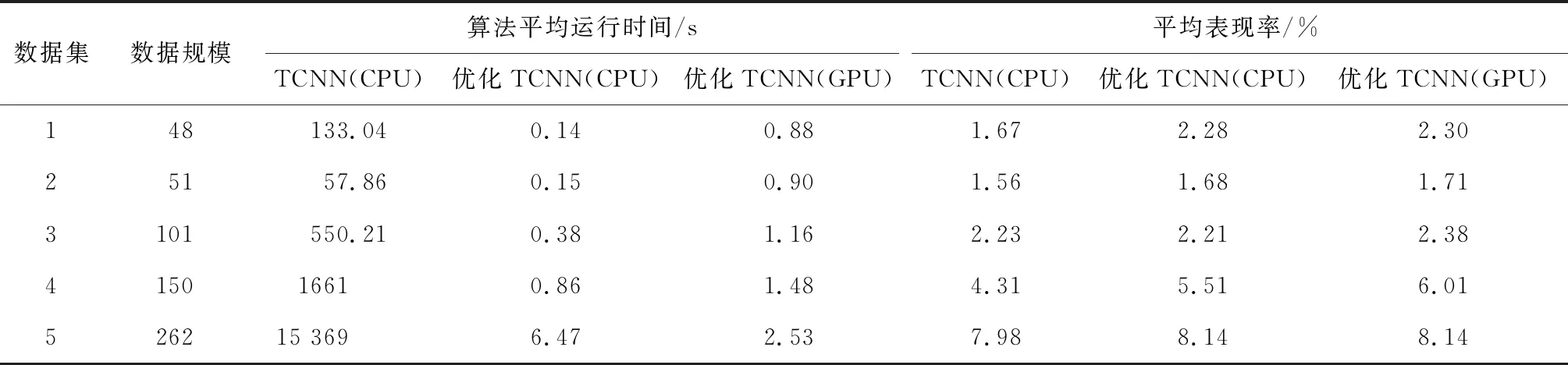
表1 并行化TCNN算法的改进效果
在表1中能够看出,并行化优化后,在CPU和GPU上运行的TCNN算法的运算速度均得到了极大的提升,处理相同的数据集时,并行化优化的TCNN算法的运行时间远低于未优化的TCNN算法。当数据规模较小时,并行化优化的TCNN算法在CPU上的计算效率更高,当数据规模超过200时,并行化优化的TCNN算法在GPU设备上的运行效率更高。这是因为研究采取将所有GPU设备的内存集中计算一个子集后,再依次计算其余子集的策略,当数据规模较小时,其效率会略低于同时计算所有子集的策略;当数据规模超过一定程度时,则能极大地提升计算速度。处理不同规模的数据集时,3种算法的平均表现率没有明显差别。以上结果表明,并行化优化TCNN能够在保证优化精度的基础上,极大地提升算法的运算速度。为验证本文提出的优化TCNN算法在处理旅行商问题上的性能,分别基于ACO算法和优化TCNN算法构建模型,利用相同的训练数据对两个模型进行充分训练后,采用相同的旅行商问题测试数据集对两种模型进行测试,测试结果如图4所示。
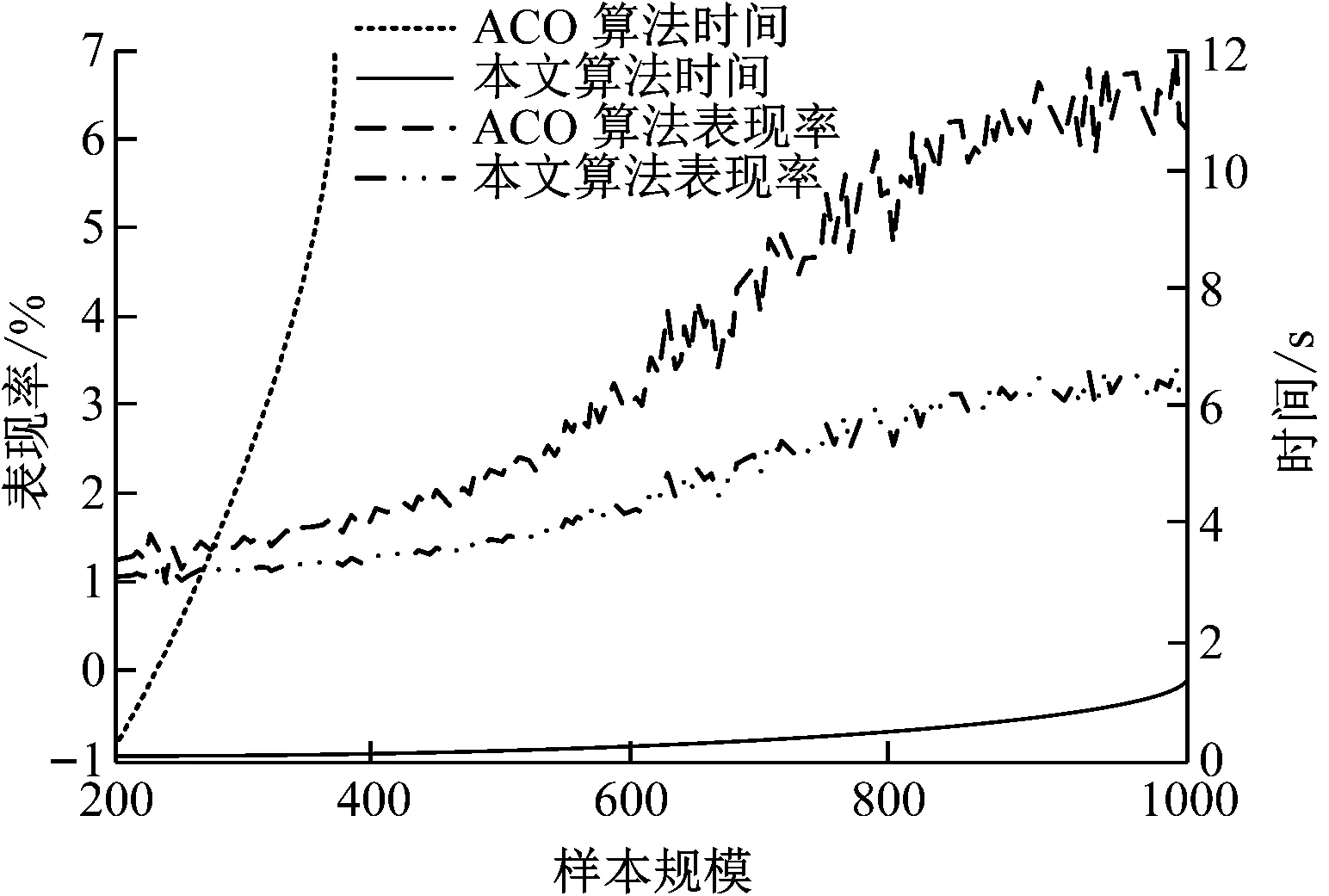
图4 优化TCNN算法处理旅行商问题的性能分析
在图4中容易看出,随着样本规模的增加,2种算法的处理时间和表现率均在增加。在样本规模达到600时,ACO算法的处理时间远超过12 s,表现率为3.03;优化TCNN算法的处理时间为0.23 s,表现率为1.73,比ACO算法低2.70。当样本规模达到800时,ACO算法的处理时间远超过12 s,表现率为5.14;优化TCNN算法的处理时间为0.72 s,表现率为2.68,比ACO算法低2.46。将算法整合到电子组装设备控制系统上位机软件中,进而优化电子组装路径。试验选择的PCB基板上需要组装的电子元器件的数目为50,分别利用ACO算法和本文提出的优化TCNN算法进行路径优化。优化后,经ACO算法优化后的路径,经改进TCNN算法优化后的路径以及连接器默认压接路径效果如图5所示。
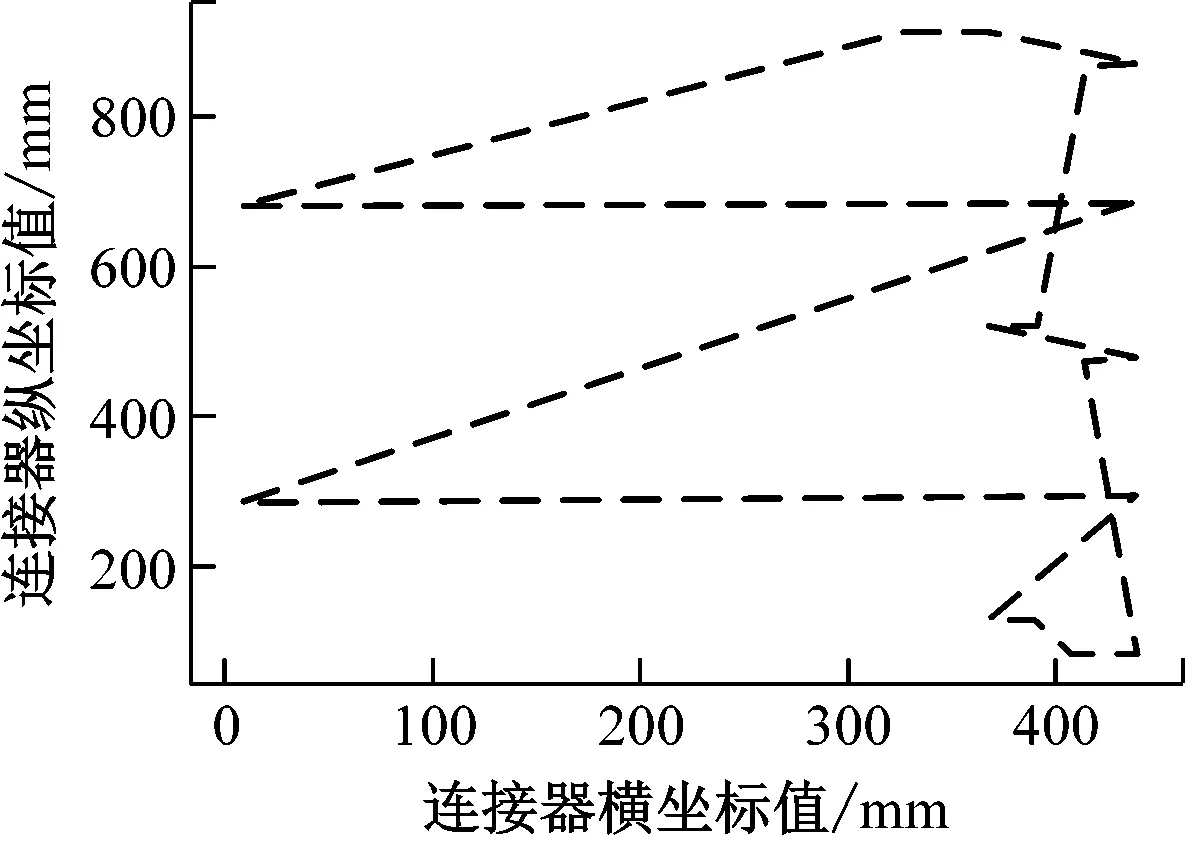
(a) 默认路径
在图5中容易看出,连接器默认压接路径有许多交叉,因此产生了许多冗余路径,导致整个路径长度较长。在经过ACO算法和改进TCNN算法进行路径优化后,交叉部分基本消除,冗余路径大大减少,总路径长度也因此缩短。其中,连接器默认压接路径总长度为3163 mm;经ACO算法优化后路径总长度为2700 mm,优化比为30.6%;经改进TCNN算法优化后路径总长度为2749 mm,优化比为28.2%。综合上述内容可以得知,研究提出的改进TCNN算法在电子组装路径优化比与ACO算法相差仅2.4%,但改进TCNN算法所需时间远低于ACO算法,更适用于大规模电子组装路径优化。
3 总结
通信背板的大规模电子组装路径优化问题关系到通信背板的生产效率,因此受到业内人士的广泛关注。电子组装路径优化问题中,传统的优化算法为ACO算法,但ACO算法的效率较低,因此研究提出一种TCNN算法,并采用并行化策略和分治策略对其进行优化和改进。仿真实验结果显示,并行化优化后,在CPU和GPU上运行的TCNN算法的运算速度均得到了极大的提升;处理相同规模的数据集时,改进TCCN算法的表现率与ACO算法的表现率无明显差距,处理时间则远低于ACO算法。将AOC算法和改进TCCN算法应用到电子组装路径优化中,ACO算法优化后路径总长度为2700 mm,优化比为30.6%;经改进TCNN算法优化后路径总长度为2749 mm,优化比为28.2%,仅比ACO算法低2.4%。综上所述,改进TCNN算法的优化精度比ACO算法略差,但优化效率远高于ACO算法,因此更适用于大规模电子组装路径优化。研究未探讨超大规模数据下算法的优化效果,还需要日后进一步研究。
