基于卷积神经网络的公交运行时间周期预测研究

武可心

(西安交通工程学院, 交通运输学院, 陕西, 西安 710300)

0 引言

公交线路的周转时间对公交运行网络的管理效率具有重要影响,直接影响公交线路的服务质量和乘客搭乘体验。周转时间是指公交车辆运行整条公交线路所需时间,主要包括车辆上行时间、下行时间和站点停靠时间。若能够对公交线路的周转时间进行准确预测,则可为公交智能调度提供关键参考数据,对提升公交网络智能管理水平具有重要意义[1-2]。

目前,公交线路周转时间的预测模型主要包括回归模型、支持向量机模型、时间序列模型、神经网络模型等。张丽莉等[3]采用RBF神经网络预测公交行驶周期,并对预测误差进行实时修正。周敏等[4]将广义回归模型应用于公交运行周期预测,将影响公交线路运行的多种因素融入预测模型。胡华等[5]结合BP神经网络和指数平滑方法,预测公交停靠时间和路段运行时间。影响公交运行时间周期的因素众多,且不同因素之间存在交错影响的关系,导致预测模型的输入因素关系复杂,使得模型输出的预测精度偏低。BP神经网络具有任意复杂的模式分类能力和优良的多维函数映射能力:从结构上讲,BP网络包含输入层、隐藏层和输出层;从本质上讲,BP算法就是以网络误差平方为目标函数、采用梯度下降法来计算目标函数的最小值。BP神经网络具有很强的非线性映射能力和柔性的网络结构,是在工程中应用最为广泛的神经网络之一,但同时其也存在学习速度慢,容易陷入局部极小值等问题。

为提升模型的预测精度和实用性,本文将公交运行过程中产生的GPS数据作为研究对象,将短时间内变动较小的影响因素作为常量考虑,例如路线长度、停靠站台布局等,重点研究时变因素对运行周期的影响,例如日期、天气、节假日等动态因素。首先通过运行周期的分布特征分析,提取影响运行周期的关键影响因素,然后将关键影响因素作为输入,利用改进型卷积神经网络对公交运行数据进行训练,以获取更为准确的预测模型。

1 公交周转时间分布特征

利用公交车配置的GPS设备,获取公交车运行的GPS数据,主要包含了车辆运行的时间、位置、速度、驾驶方向等动态数据。将公交车GPS数据作为研究对象,利用有序样本聚类方法对公交运行时间进行划分,然后对公交运行时间周期进行分布特征分析。在不同的时间段内公交运行时间周期是不同的,通过大量的运行数据统计,重点分析不同时间窗内公交运行时间周期的分布情况,从而提炼出影响公交运行时间周期的关键因素。图1为某路公交2个月的运行时间周期统计结果,通过运行周期分布曲线图可看出,运行时间周期随全日工作时间呈现出一致性的规律变化,在单个时间窗口内,运行时间周期呈现一定的噪声波动,波动规律趋近于正态分布。单个时间窗口内运行时间周期的近似正态分布图[6]如图2所示。

图2 单时间窗内运行时间周期分布图

对于单条公交线路,线路距离、站台数量可看作不变量,影响公交运行时间周期的动态因素主要为天气、客流量、节假日、气候等,而动态影响因素之间相互关联,呈现出复杂的非线性特性,由上述统计曲线可知,单个时间窗口内运行时间周期呈现正态分布特性[7]。根据公交周转时间分布特征,将影响运行时间周期的主要动态因素进行统计,并将主要影响因素作为输入量,利用改进型卷积神经网络对样本数据进行训练,经过反复学习迭代,获取公交运行时间周期预测模型。

2 改进型卷积神经网络预测模型

卷积神经网络的多隐层有利于提取数据特征,但过度增加网络卷积层数量,将会降低卷积神经网络的运行效率,导致网络性能下降。对卷积神经网络的改进主要分为2个方面,一方面是适量提升卷积层数量,另一方面是适当修改卷积核的尺寸。本文选取9种典型卷积神经网络结构分别进行性能测试,测试统计结果[8-10]如表1所示。

表1 多种典型卷积神经网络结构测试结果

由表1可知,在卷积核尺寸一样的条件下,卷积层数目为3时卷积神经网络的预测准确率最高。另外,在卷积层数目相同的条件下,卷积核尺寸为3×3时,卷积神经网络的预测准确率最高。为保证卷积神经网络具备较高的准确率,并避免网络规模过大,网络结构的卷积层选为3层,卷积核尺寸选为3×3。

通过网络结构的优化,虽能够提高卷积神经网络的性能,但同时造成了过拟合问题。过拟合主要是由于卷积神经网络的连接层参数是按照训练样本的识别结果进行更新的,若训练样本的分类不够成熟,则会导致测试数据无法获得准确的预测结果。采用Dropout技术对训练过程中的参数按照一定的概率进行随机抛弃,从而提升神经网络的泛化性能。Dropout技术主要是在训练过程中将每层的神经元按照一定比例进行随机剔除,从而保证每层网络的输入数量和输出数量相同[11-12]。未加入Dropout技术的网络训练过程可表示为

(1)

加入Dropout技术的网络训练过程表示为

(2)

式(2)中,l表示隐含层索引序号,z表示输入向量,y表示输出量,w表示每层的加权系数,f表示激活函数,p表示预测前每个单元参数的预乘系数。

卷积作用主要是对数据特征进行提取,提取数据特征越精细,获得的预测结果越精准。在卷积神经网络中,通过卷积层和池化层可交替生成数据通道。在数据训练过程中,若仅采用单一的数据通道和网络结构,易导致数据的特征提取不充分。针对公交运行时间周期和影响因素数据的特点,提出一种双数据通道方法,采用2条不同的通道,分别对不同的特征进行卷积运算,利用2条通道的级联运算获得最终的网络数据结果。主要过程包括利用Dropout技术获取降维数据,然后将降维数据通过2个通道进行运行,第一个通道采用3×3的卷积核,数据进行卷积运算后,另一个通道在第一个通道的基础上进行残差运算。最后对2个通道进行级联操作,获得1个新特征图。残差运算网络的短接映射关系[13]可表示为

(3)

式(3)中,x表示输入元素,F()表示残差拟合函数。

采用双通道级联方式,通过两路卷积神经网络进行级联运算,其中一路包含了残差运算模块,并对两路不同特征数据进行组合,获取最终的输出。

设定训练样本为(xi,yi),样本数量为m,输入向量的维度为n+1,卷积神经网络的输出类数量为k,卷积神经网络的输出可表示为

(4)

式(4)中,θj表示卷积神经网络的第j个参数。

代价函数J(θ)可表示为

(5)

式(5)中,p表示输出结果的概率分布,1{·}表示指示函数,λ表示正化系数。

卷积神经网络每次进行迭代运算后,参数的更新表达式可表示为

(6)

式(6)中,α代表学习速率系数。

基于改进型卷积神经网络的公交运行周期预测模型的框架图[14]如图3所示,从整个模型结构可知,该模型主要由输入层、隐含层、输出层构成,并分为了模型训练和模型预测2个数据传输通道,并将影响公交运行周期的主要因素数据作为输入,通过输入层的全连接处理,并经过隐含层卷积运算后,再经过输出层的全连接网络将隐含层的输出映射到最终输出结果,实现公交运行数据的特征提取和分类,从而完成对公交运行周期的预测。

图3 基于改进型卷积神经网络的公交运行周期预测模型

3 实验结果

以某公交线路运行数据为研究对象,整条公交线路的下行站点为37个,上行站点为38个,全日车辆运行时间区间为6:00-21:00。首先利用有序样本聚类方法对运行时段进行分类,在损失函数达到最小值时,获得14个长度不等的时间窗口。由于单个时间窗口内运行时间周期整体呈现正态分布特性,数据分布特性的统计需要尽量多的统计数据,若时间区间段划分过多,则获取的数据量数目过少,导致统计特性易受噪声影响,数据特征被噪声淹没,且过多的区间段划分隔断数据间的相关性和增加运算量;而过少的时间区间段划分,不利于凸显不同运行区间内公交运行特征的差异。根据在一天中公交运行的整体分布经验,可将14个时间窗口划分为5个区间段,分别为早低峰、早高峰、平峰、晚高峰、晚低峰,时间窗划分情况如表2所示。

表2 时间窗口划分

将影响公交运行时间周期的主要动态影响因素作为卷积神经网络的输入,主要包括时间窗、节假日、天气、季节、星期,网络输出结果为公交运行周期的预测结果。共选取600组数据作为样本,将其随机分为2组:第一组为训练样本,共300组数据;另外一组为测试样本,共300组数据。

改进型卷积神经网络采取双隐含卷积层结构,输入层共有6个输入量,分别对应时段、天气、节假日、星期、季节、运行周期等6个因素。第一个隐含卷积层节点为9个,第二个卷积层节点数为7个,输出层节点数为1个,经过卷积层的信息传递和节点调整,进行反复的训练迭代。卷积神经网络输出精度的评价指标采用绝对百分比误差,表达式为

(7)

式(7)中,t1表示公交运行时间周期的预测值,t2表示公交运行时间周期的的实际值。

为了对比算法的预测精度,将BP神经网络与本文算法进行对比:2种算法的预测值与实际值的对比结果如图4所示,BP神经网络的平均预测精度为16.7%;本文改进型卷积神经网络的样本预测误差统计如图5所示,本文改进型卷积神经网络的平均预测精度为5.2%,预测精度得到明显提升。实验结果验证了改进型算法的预测精度和有效性。

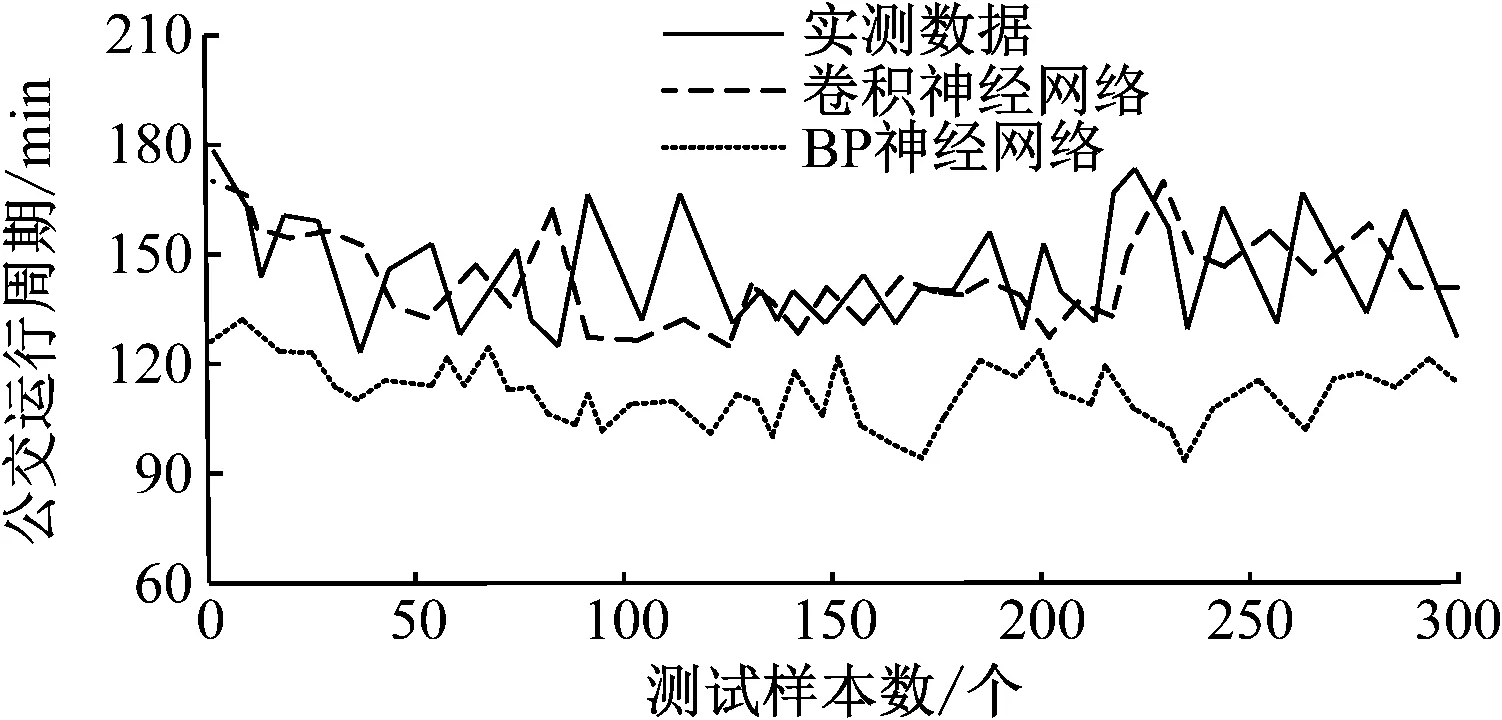
图4 2种算法的预测值对比结果

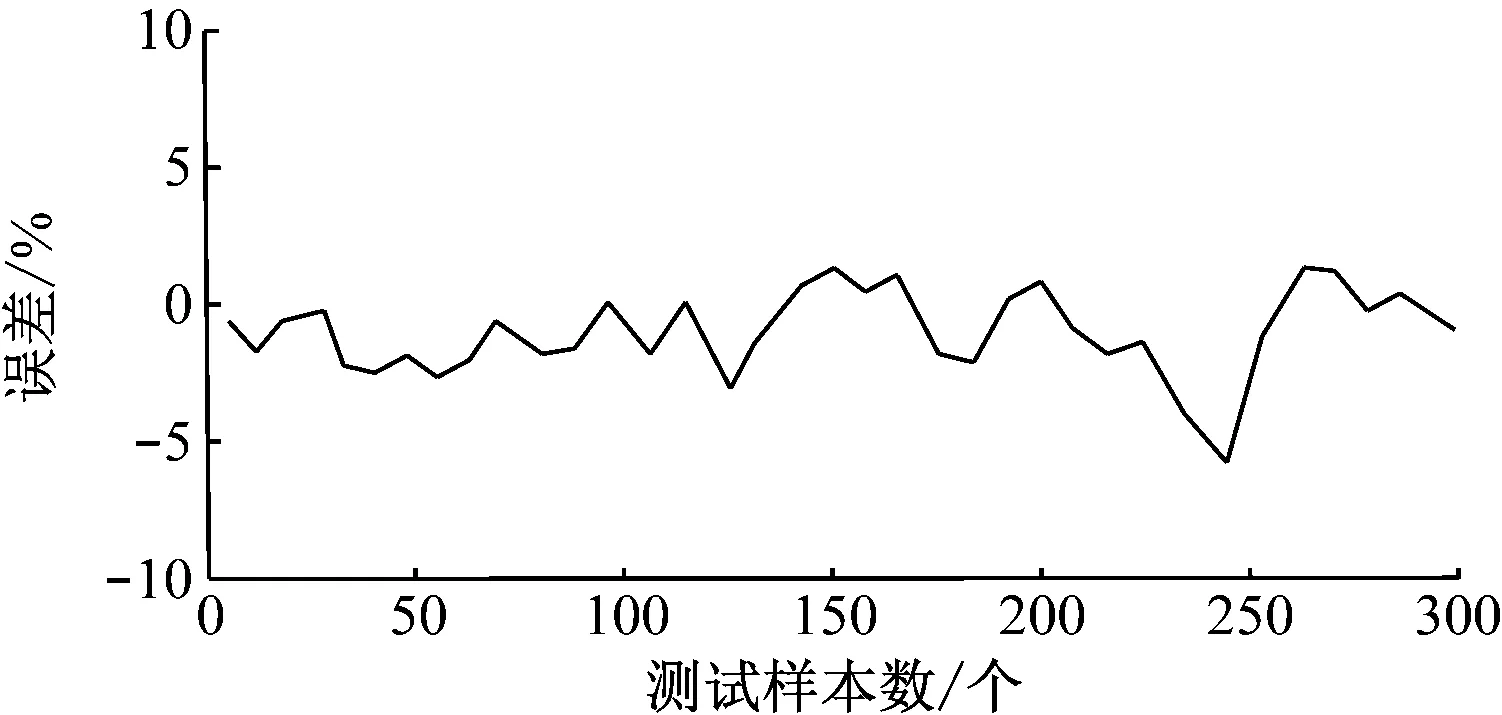
图5 改进型卷积神经网络的样本预测误差统计

4 总结

为了提升公交线路运行效率,针对公交运行时间周期预测问题,本文提出了一种基于改进型卷积神经网络的预测模型。将影响公交运行周期的关键动态因素作为输入,分析影响因素的非线性分布特征,将运行时间按照时间窗口进行划分。从卷积层数量和卷积核尺寸2个方面对卷积神经网络进行改进,并建立2条级联的数据运算通道,构成改进型卷积神经网络模型,实现对公交运行时间周期的有效准确预测,实验结果验证了该预测模型的可行性。