基于Newton-Raphson 法的非线性方程组求解研究
2024-01-12郭华毅
郭华毅
(山西药科职业学院,太原 030031)
数值计算中,最困难的问题之一是非线性方程组的求解。非线性方程组的求解由于没有指定的求解公式,因此在实际操作中很难得到精确的解〔1〕。常见的求解非线性方程组的方法有梯度法、共轭方向法、抛物线逼近法、迭代法等〔2〕。在解决实际的数学问题中,要根据不同的条件灵活运用方法,不同的求解方法有着不同的优缺点。梯度法作为求解方法中最古老的方法之一,可以任意选择初始点,并且每次迭代的计算量小,存储量也少,因此它的程序也较为简短〔3〕。可以从一个随意的甚至不好的初始点出发,开始几步迭代后慢慢逼近局部的极小点,但它也有自己的不足之处。因为它逼近的是一个局部的极小点,缺少整体性,从整体的角度来看,这不一定是收敛速度最快的方向。其次,梯度法只用到一阶导数的信息,不适合用于二阶非线性方程组的求解〔4〕。对于共轭方向法而言,则还需要选定方向,要求满足共轭条件和下降的条件,并且每一次都要重新并反复确定搜索方向,操作量比较大,在求解非线性方程组的过程中会消耗大量的时间〔5〕。为了弥补此类方程在实际解决非线性方程组解法上的不足,便可以用牛顿-拉弗森(Newton-Raphson)法,Newton-Raphson 法是求解非线性方程组最经典的方法之一。Newton-Raphson 法也叫作牛顿迭代法,它可以适用于高阶的非线性方程组,并且也不用像共轭方向法那样,周而复始地搜索方向〔6〕。Newton-Raphson 法在迭代的过程中,只需要迭代几次就可以轻松地得到非常精确的非线性方程组的解,并且通过Newton-Raphson 法还可以求方程组的重根和复根。该方法最大的特点在于将非线性问题进行线性化,简化了求解过程。Newton-Raphson 法还可以求解一些代数方程和超越方程〔7〕。本研究通过解析Newton-Raphson 法的基本原理,并结合案例分析证明该方法在非线性方程组求解中的实际应用。
1 Newton-Raphson 法的求解过程概述
1.1 Newt on-Raphson 法的迭代原理Newton-Raphson 法的基本思想:把一个非线性方程线性化,再用线性方程的解去逼近非线性方程的解。首先,针对一个一元非线性方程,在实现非线性方程的线性化过程中,可以对该非线性方程做一阶泰勒展开。对于一个一元函数f(x)=0,取x0≈x*,对f(x)在x0处做一阶泰勒展开:
其中ζ 在x0和x 之间,取x≈x*,那么把x0)2看作高阶无穷小量,则有
方程f(x)=0 可以近似地表示为f(x0)+f '(x0)(x*-x0)=0,其中f(x)=0 的根x=x*。
对于这个线性方程,可以记其近似根为x1,那么x1的计算公式为:
做k+1 次迭代,即得牛顿迭代公式
即方程f(x)=0 的根x*在几何上可理解为曲线y=f(x)与x 轴交点的横坐标。若xk是根x*的一个近似,那么过曲线上横坐标为xk的点Q(xk,f(xk))作曲线y=f(x)的切线,则这条切线lk与x 轴交点的横坐标即为xk+1,见图1。
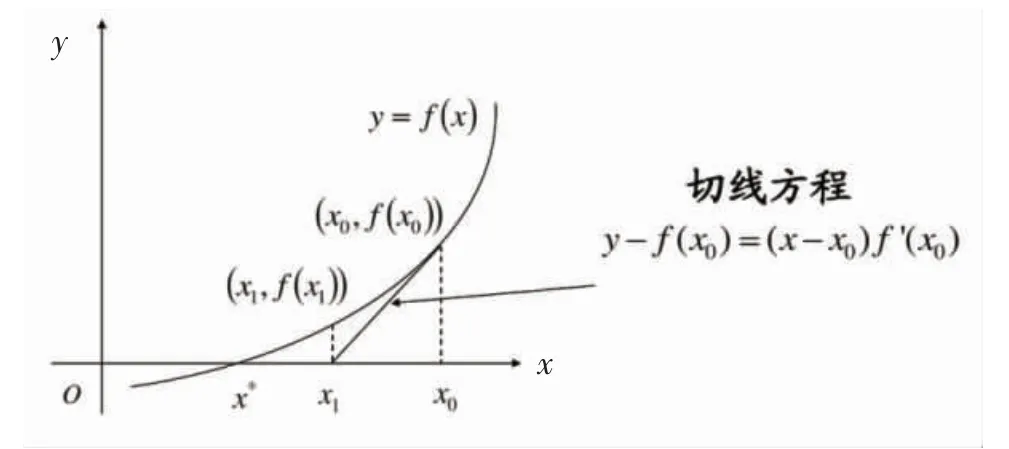
图1 Newton-Raphson 法的几何意义
1.2 Newton-Raphson 法对二元函数方程组的求解对于二元函数而言,也可通过泰勒公式展开。设z=f(x,y)在点(x0,y0)的某一邻域内连续,且直到(n+1)阶都有连续的偏导数,在该邻域上的任意一点Q(x0+h,y0+k),则有:
设z=f(x,y)在点(x0,y0)的某一邻域内连续且直到二阶有连续的偏导数,邻域内任意的一点(x0+h,y0+k),有
方程f(x,y)=0 可近似地表示为
即
同理设z=g(x,y)在点(x0,y0)的某一邻域内连续且直到二阶有连续的偏导数,该邻域内任意的一点(x0+h,y0+k),同样有
方程g(x,y)=0 也可近似地表示为
即
根据f(x,y)=0 和g(x,y)=0,通过联立方程组,转化为求解非线性方程组的问题。
得到的方程组为:
从而有
于是,可以简化方程组,
那么方程组可以改写为:
则方程组的迭代公式可以写为:
通过迭代公式(8),便可以求出当k=1,2,3,…时(xk,yk)的值,当≤δ 时,此方程组的根为(xk,yk)。
1.3 Newton-Raphson 法对多元函数方程组的求解令fi(x1,x2,…,xn),i=1,2,3,…,n 是n 个定义域在n维空间区域D 的n 元函数,且二次连续可微,它的值域也在D 内。该解可表示为,可以同样参照一元函数的求解过程,把fi在点附近的一点(x01,x02,…,x0n)进行泰勒公式展开,可得
这样完成了通过泰勒展开公式把一个非线性方程组转化为一个线性方程组的过程。对于此线性方程组的根x01,x02,…,x0n,就是原非线性方程组的根的近似值。此线性方程组中对于未知数x1,x2,…,xn的系数矩阵即可写成Jacobi 矩阵
令f=(f1,f2,…,fn)T,x=(x1,x2,…,xn)T,x0=(x01,x02,…,x0n)T,则Jacobi 矩阵可以写作f(x0)+J(x0)(x-x0)=0,对该方程进行求解得x1=x0-J-1(x0)f(x0)。反复进行求解,便可以得到对于多元方程组Newton-Raphson 法的迭代公式,即
2 数值分析
例1 用Newton-Raphson 法求解方程组
解:
令
该方程组的系数矩阵
即
选取初始值x(0)=(0,0)T,解方程J(x(0))△x(0)=-f(x(0)),即解方程组
其解为△x(0)=(0.8,0.88)T。解方程组J(x(0))△x(0)=-f(x(0)),按Newton-Raphson 法进行迭代计算,结果见表1。

表1 Newton-Raphson 法计算结果(k=0~5)
本研究通过分析牛顿迭代公式在一元非线性方程的求解过程,结合多元函数泰勒展开式给出了非线性方程的牛顿迭代公式,同时给出了非线性方程组的牛顿迭代公式,并通过具体的算例验证了方法的正确性。
