基于高考题分析高中数学解题的审题技巧

李瑞奎

【摘  要】  在高考题中数学占据较大比重，其重要性不言而喻.对于高中学生来说，通过数学知识的学习能够为物理与数学结合知识点学习提供基础，也为学生学习兴趣的提升提供有效途径.但是因高中数学具备较强的抽象性和复杂性，如果学生欠缺良好的审题技巧和解题思路，其难度较大，就会让学生逐渐产生恐惧心理，打击学生对数学学科的兴趣.

【关键词】  高中数学；审题技巧；解题技巧

正确审题是高考题解题的关键环节，如果在审题的过程中学生的思路出现偏差，将难以把握题目中所隐含的知识点，从而难以正确高效地解出正确答案.

1  把握已知條件

在数学解题中，已知条件是关键组成部分，通过对已知条件的把握才能够确定大致的解题思路，因此已知条件的把握是解题中不可或缺的步骤.

例1  （2021全国卷）在直角坐标系xOy中，⊙G的圆心为G（2，1），半径为1.

（1）写出⊙G的一个参数方程；

（2）过点F（4，1）作⊙G的两条切线，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求出这两条切线的极坐标方程.

知识点考查：曲线的极坐标方程和圆的参数方程.

解析  （1）先求出⊙G的标准方程，从而求出⊙G的参数方程.根据题目中的已知条件可知⊙G的圆心为G（2，1），半径为1，

从而得到⊙G的标准方程为

，

由此得出⊙G的参数方程为

（θ为参数）.

（2）直接求出直角坐标系中的切线方程，只有将，带入其中，从而求出这两条切线的极坐标方程.根据题目中的已知条件可知两条切线方程斜率存在，

那么设切线方程为，

那么，

圆心G（2，1）到切线的距离=1，

从而求出k的取值为±，

所以切线方程为，

因为，，

所以求出这两条切线的极坐标方程为

.

在本道题目解析的过程中主要考查圆的参数方程，普通方程与极坐标方程之间的转化以及运算求解能力.因此在解析的过程中学生要明确题目中的已知条件，从而做出正确的判断，完成题目的解答.

在上述题目解析的过程中主要是考查学生的计算能力以及各个变量的计算公式，因此在此类题型解析的过程中需要把握题目中的已知条件，正确地审题，从而得出最后的答案[1].

2  分析条件与目标联系

所有的数学问题都是由若干条件和一个核心结论组成，因此在在审查高考数学试题的过程中，要对现有的条件进行分析，通过列举的方式明确已知条件，并对条件进行分析，与此同时还要分析题目所要达成的目标，从而找出目标与条件之间的关系，通过目标和条件的列举思考解题思路和技巧，从而顺利完成题目的解答.

例2  （2021全国卷）已知集合，，则（   ）

（A）.    （B）S.    （C）T.    （D）Z.

本道题目中主要考查交集与运算，因此分别讨论当n为偶数或奇数的时候集合元素情况，之后结合集合的基本运算进行判断.

解析  当n为偶数时，设，则，当n为奇数时，设，则，则，所以答案选（C）.

分析条件与目标之间的关系是高考数学审题中较为常用的方式之一，通过列举的方式将交集中的可能性进行分析，从而求出问题的答案，因此在数学问题解析的过程中教师可以引导学生对已知条件进行分析，明确其与目标之间的关系，最后求出问题的答案[2].

3  找出隐蔽条件

在数学问题解析中，部分问题中包含较为隐蔽的条件，通过隐蔽条件的找寻能够让学生明确解题的思路，从条件推导出结论，分析条件与结论之间的关系，确定内在联系，从而准确地利用自己现有的数学知识和原理对数学问题进行解答.

例3  （2021全国高考卷）设，直线被抛物线所截，那么被截线段中点的方程式是什么？

在本题解析的过程中，学生较为容易受到惯性思维的影响，在审题时直接使用代入法，直接将直线方程代入到抛物线方程当中，利用部分韦达定理换算得出最后的结果.但是代入法在解题中步骤较为繁琐，会浪费大量的时间，因此需要合理地利用方法思维，对方程进行全面分析.

根据观察可知点在直线与抛物线上同时存在，那么可以设中点，从而得出截线段KJ的另一个端点，之后将J点的坐标代入到方程当中，从而得出中点轨迹方程.

在上述解析的过程中，我们需要先找出题目中的隐蔽条件，从而根据已知条件与结论之间的关系，明确解题思路和方法，在最短的时间内计算出问题的答案，提高解题的效率 .

4  数形结合

在数学问题解析中，数形结合也是较为重要的形式之一.因高中知识点较为抽象和复杂，因此数形结合的解题思想应用较为广泛.

例4  （2021全国卷）设，若为函数的极大值点，则（   ）

（A）.   （B）.   （C）.  （D）.

本道题目主要是利用导数研究函数的极值，主要考查三次函数的图象及性质，通过导数知识的运用和数形结合思想求解问题.

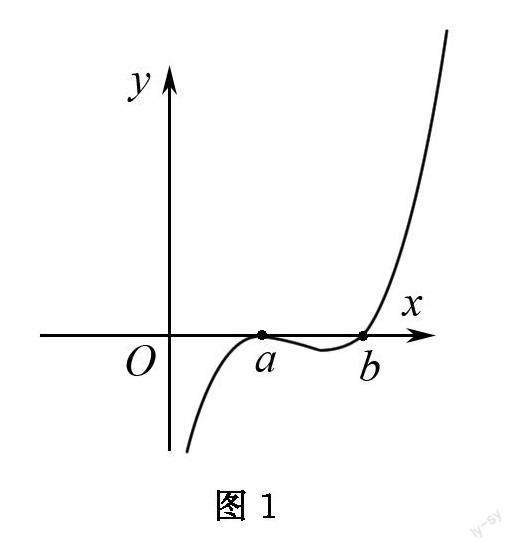
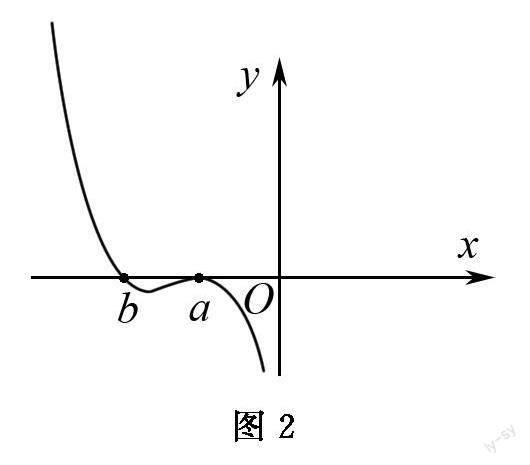
图1                           图2

解析  令，解得或者是，即及为的两个零点，当的，通过三次函数的性质可知，要使得是的极大值点，那么函数的大致图象如图1所示，则；

当的，通过三次函数的性质可知，要使为的极大值点，那么函数的大致图象如图2所示，则.

综合以上得出正确的选项为（D）.

通过上述解析过程可以看出，在高中数学函数问题中，通过数形结合的方式将原有抽象的问题变得更为直观和清楚，不仅简化了问题解决的思路，并且相对于传统的解题过程来说，将数据和图形进行结合的方式更能够让学生明确数学问题当中存在的对立关系，从而在较短的时间内掌握解题的思路和方法，为解题效率的提升提供了有效保障.

5  结语

综上所述，高考数学试题审题技巧的核心就是在基础知识全面掌握的前提下，帮助学生形成审题思路，找对方法，使其拥有良好的审题观念，从而在解题的过程中形成正确的思路和方法，尽可能拿到分，取得较好的成绩.

参考文献：

[1]钱春艳.数形结合思想方法在高中数学教学与解题中的应用[J].文理导航（中旬），2022（03）：64-66.

[2]师喜景.寻找快乐学习的钥匙——以高中数学“导学”概念教学为例[J].试题与研究，2022（04）：6-7.