高观点下几何证题中的动态方法及投影方法

徐境鸿

【摘  要】  利用动态以及投影的方法处理一类几何问题，是解初等几何题的一种重要的思想方法.本文就一道经典的关于三棱锥的数学竞赛题，通过动点轨迹的变化和顶点的不同投影等变式，利用以上两种方法展开变式探究，简单探讨如何解决高观点下的初等数学问题.

【关键词】  高中数学；动态方法；投影方法

实践证明，利用动态以及投影的方法处理一类几何问题，将收到事半功倍之效，它不失为解初等几何题的一种重要的思想方法.在数学竞赛及中高考试题中，我们经常会遇到此类问题.

1  动态以及投影方法概述

众所周知，几何学是研究几何体的性质——形状、大小和相互位置关系的一门学科.早期的人们只研究静止的图形，随着研究的深入，才逐步引入了动态的观点，把图形之间的位置关系看作是处在变化的、相互依存的状态之中.这里所说的“动”，是指欧式运动，即平移、旋转和反射三种基本运动所形成的运动群.在高等几何里，仿射变换、射影变换已有广泛应用，但这些“高观点”在中学几何上是否用得上呢？结论是肯定的.比如在中学集合中，有证明笛莎格定理等著名定理的.

所谓投影，一般有以下几种：

（1）从一点向平面所作垂线的垂足，就称这点在平面上的正投影，简称投影.

（2）一条直线在一个平面内的投影，就是这条直线上所有的点在这平面内投影的集合.因此，只需将直线上的两个点向平面作投影，则平面上连接这两点的投影的直线，叫做已知直线在平面上的投影.

（3）所谓面积投影定理，是指设一封闭图形面积为S，其在投影面M内的投影面积，封闭图形所在平面和投影面M所成之角为，则.

投影方法是实现把空间问题转化为平面问题的一种重要途径.把空间一点向平面投影，投影点落在什么位置，有时往往成为解决问题的关键.

下面我们就以一道经典的上海市中学生数学竞赛题进行简单的变式探究.

2  试题呈现

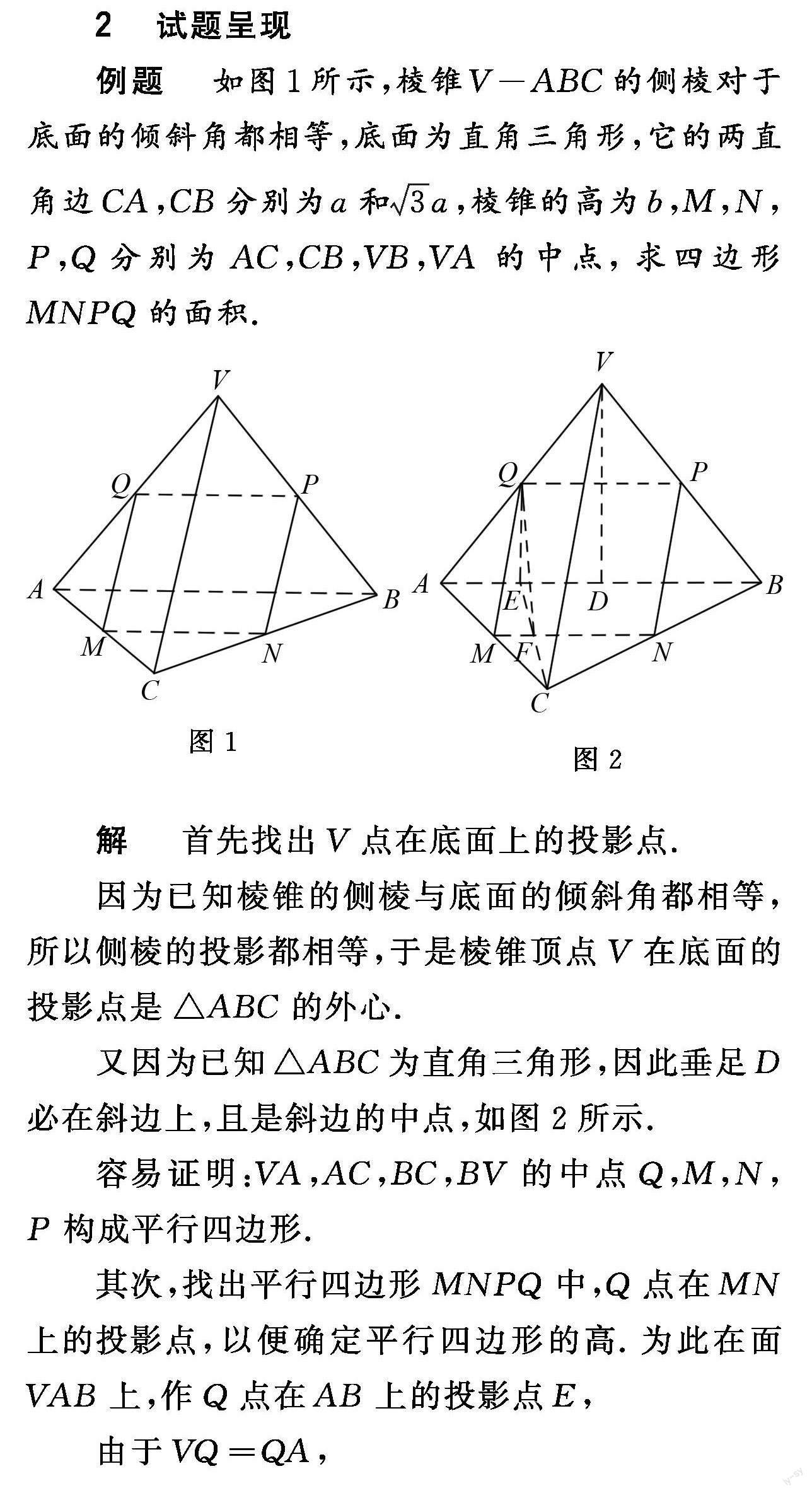
例题  如图1，棱锥V-ABC的侧棱对于底面的倾斜角都相等，底面为直角三角形，它的两直角边CA，CB分别为，又棱锥的高为b，M、N、P、Q分别为AC、CB和VB、VA上的中点，求四边形MNPQ的面积.

解  首先找出V点在底面上的投影点.

因为已知棱锥的侧棱与底面的倾斜角都相等，所以侧棱的投影都相等，于是棱锥顶点V在底面的投影点是的外心.

又因为已知为直角三角形，因此垂足D必在斜边上，且是斜边的中点，如图2.

容易证明：VA、AC、BC、BV的中点Q、M、N、P构成平行四边形.

其次，找出平行四边形MNPQ中，Q点在MN上的投影点，以便确定平行四边形的高.为此在面VAB上，作Q点在AB上的投影点E，

由于VQ=QA，

AE=ED.

如圖3，在中，，又D是斜边中点，因此为正三角形，

在中，设

，

因此QF即为平行四边形之高.这样，设平行四边形的面积为S，则

，

.

3  变式探究

3.1  动态方法：当a，b满足一定的条件时，求S的最值

（1）当在单位圆上运动时，即当时，求S的最值.

解  .

当且仅当时等式成立.但我们发现它们不可能相等，所以无最值.

（2）当在椭圆上运动时，即当时，求S的最值.

解  .

当且仅当，等式成立.

.

3.2  投影方法：当V点在底面的射影分别是三角形的垂心和内心时

3.2.1  当V点在底面的射影是三角形的垂心时

解  如图4所示，由三角形垂心的性质可知，点V在底面的投影正好是点C，

，

.

，

，

.

3.2.2  当V点在底面的射影是三角形的内心时

方法1  投影法

分析  如图5所示，V点在底面的射影即三角形ABC的内切圆的圆心，设为O.连接OA，OB，分别取它们的中点，再把连起来，则平面即为平面QPNM的射影面.设两平面所成的角为，利用射影的知识不难知道.由求，由求，在直角三角形中可求得到，关键就是求出.，所以.

详细解答过程略.

方法2  向量法

分析  以点C为原点，CB所在直线为x轴，CA所在直线为y轴，与OV平行的直线为Z轴，建立空间直角坐标系O-xyz，可求得内切圆半径即OD的长为，因此易得各点坐标.通过公式，可求得的正弦值，所以.

详细解答过程略.

3.3  其他变式：当是边长为a的正三角形时

分析  因为“三心”合一，所以不管V点在底面的射影是外心，垂心，还是内心，方法都是一样的.

如图6所示，可求得，

从而得到.

易证得四边形PQMN是矩形，

所以.

在解决三棱锥问题时常常要解决三棱锥的高，只要抓住了垂足在底面上的位置，问题就容易解决.因此，掌握在各种条件下三棱锥顶点在底面上射影位置，是解决三棱锥问题的关键.

4  教学建议

（1）动态方法可以帮助学生更好地理解几何问题的性质和关系，通过观察动态场景中的变化，可以培养学生的几何直觉和推理能力.射影方法是解决立体几何问题的重要方法，通过观察和分析投影变化，可以揭示几何体的内在本质.

（2）在教学中，可以引导学生主动构造动态场景，通过拖动和观察来解决几何问题，激发学生的兴趣和主动性.可以使用模型或计算机模拟等工具来展示几何图形在平面上的投影变化，帮助学生直观地理解射影的概念和原理.

（3）在引导学生进行动态方法解题时，可以提供一些提示和引导，帮助学生思考如何调整场景中的元素以获得更多的信息和线索.引导学生观察和思考几何图形在不同角方向和角度的投影变化，培养他们的几何直觉和推理能力.

（4）鼓励学生在解决问题过程中思考和讨论，培养他们的合作能力和团队精神，同时也可以促进他们对几何问题的深入理解.鼓励学生在解决问题过程中进行实际操作和实验，通过动手实践来加深对射影方法的理解和应用.同时，也可以引导学生进行讨论和交流，分享彼此的思考和发现.

5  结语

一个数学教师的职责之一，是“应使学生了解数学并非孤立的各门学问，而是一个有机的整体”；德国数学家克莱因指出，“有关的每一个分支，原则上应看做是数学整体的代表”，因此有众多初等数学的现象只有在非初等的理论结构内才能深刻地理解.一个称职的教师应当掌握数学的各种概念、方法及其发展与完善的过程，了解数学历史和数学教育演化的经过，基础数学的教师应该站在更高的视角（高等数学）来审视、理解初等数学问题，只有观点高了，事物才能显得明了而简单.

参考文献：

[1]Felix Klein.Elementary Mathematics from an Advanced Standpoint[M].上海：复旦大学出版社，2008.

[2]张奠宙.现代数学与中学数学[M].上海：教育出版社，1990.

[3]陶铁群.中学数学教与学（高中版）[J].江苏高教，1997（07）.