基于Mathematica的物理教学资源开发
--以波动现象的动态模拟为例
2024-01-11张斯博刘思雨宋思盈洪许海周兴玉
张斯博,刘思雨,宋思盈,洪许海,周兴玉
(辽宁师范大学 物理与电子技术学院,辽宁 大连 116029)
中共中央、国务院印发《中国教育现代化2035》指出:“信息技术促进了教育的发展,计算机辅助教学是信息化时代的必然产物”。新时代的物理教师在掌握传统教学技能的基础上,也要掌握现代化的计算机工具,大力开发数字资源,推进物理教学改革与创新,使学生切实受益。当代大学生成长于信息时代,运用计算机辅助学习已是一项基本技能。在计算物理日益重要的今天,物理学专业的大学生更要充分利用先进的计算机软件促进自己的学习,为自己将来的职业发展打下基础[1,2]。
Mathematica[3]作为一款功能强大、用法简单、语法优雅的数学软件,在理工科教学方面,特别是物理教学方面,有着广阔的应用空间[4-8]。在物理学中,有些现象比较抽象,仅依靠传统教材中的文字、公式和图片,学习者难以在脑海中构建出具体的图像,而利用Mathematica软件强大的图形绘制功能和便捷的动画合成功能将抽象枯燥的公式转化为形象直观的动画,则可以很好地解决这一问题。而且,这种方法不受实验仪器及其精度的限制,可以有效地节约成本。
波动现象是一类重要的物理现象,是大学物理教学内容的重要组成部分[9]。本文以经典物理学中几种典型波动现象的动态模拟为例,来介绍基于Mathematica的物理教学资源开发。具体而言,本研究使用Mathematica软件对声波的行波和驻波,简谐水波在多视角下的三维图像,通过单缝和双缝的光波在传播空间中的强度分布图像,以及平面电磁波的传播做动态模拟,以期得到直观形象的动态效果图,帮助学习者更好地认识波动现象和理解波动规律。
在精确模拟这些波动现象的过程中,本研究充分利用了Mathematica强大的内置函数,特别是以下五种绘图函数:ListPlot(绘制点集)、Plot3D(绘制三维图形)、DensityPlot(绘制密度图)、Graphics3D(绘制三维形状)、ParametircPlot3D(绘制三维参数图)。创作相应的动态效果图时,本文采用的一般步骤如下:首先,使用ListPlot等函数绘制某个波动现象的静态图;然后,通过Table(表格)函数控制变量生成一系列渐进变化的静态图;最后,使用Export(导出)函数将该系列静态图按顺序合成并输出为一个动态图。
1 声波的行波和驻波
根据传播方向与振动方向的关系,波可以分为横波和纵波。相比于横波,纵波的物理图像更难想象。声波是一类典型的纵波。在声速测量实验[10]中,行波法(相位比较法)和驻波法(振幅极值法)被用来测量超声波的速度。在教学过程中可以发现,对于声波之行波和驻波的传播形态,很多同学的认识比较模糊。为了帮助同学们建立清晰的物理图像,本节使用Mathematica软件对声波的行波和驻波做动态模拟,其中用到的行波和驻波的波动公式分别为
x(x0,t)=x0+Acos(ωt±kx0+φ) ,
(1)
x(x0,t)=x0+Acos(ωt±kx0+φ1)+Acos(ωt∓kx0+φ2) ,
(2)
其中,x0为质点的平衡位置,x为质点在t时刻所处的位置,A代表振幅,ω代表圆频率(ω=2πf,f为频率),k代表波数(k=2π/λ,λ为波长),φ、φ1、φ2代表相位。在此值得说明的是,本文所研究的波动现象并不局限于某一特定的时空尺度,相关物理量的绝对数值及具体单位不是影响仿真效果的核心要素,为表述方便,对于这些物理量本文采用相对数值的表达方式并省略了它们的单位。
基于波动公式(1),在Mathematica中输入并执行如下语句
A=1;ω=1;k=1;φ=0;φ1=0;φ2=0;m=270;n=20;


Table[{x0[i]+A*Cos[ω*t-k*x0[i]+φ],y0[[i]][[j]]},{i,m},{j,n}],1],
PlotRange→{{-1,6π+1},{-1.25,1.25}},
PlotMarkers→{Automatic,Tiny},PlotStyle→Black,Axes→False];
images=Table[image[t],{t,0,2π,2π/180}];
Export[“声波之行波.gif”,images,“DisplayDurations”→0.05,
ImageSize→{720,360},“Animation Repetitions”→6]
程序运行界面如图1所示,Mahtematica软件会自动显示代码中关键词的汉语翻译。输入代码后,按Shift+Enter键或直接按小键盘Enter键执行该程序,即可在当前工作目录(Windows系统中默认为“文档”文件夹)下生成gif格式的动态效果图文件:声波之行波.gif,如支持信息中动态图S1(a)所示,这里使用点集运动来表现声波之行波的运动形态,其中的“点”代表组成介质的微粒。

图1 程序运行界面
这段程序分为三个步骤。第一步的image函数定义分为三层。其中,最内一层的Table函数,用来产生图中点的集合,该函数包含以下三个参数:(1){x0[i]+A*Cos[ω*t-k*x0[i]+φ],y0[[i]][[j]]}是点的坐标表达式,其中x0[i]和y0[[i]][[j]]是第(i,j)个点的平衡位置的横纵坐标,A*Cos[ω*t-k*x0[i]+φ]是该点相对于平衡位置的振动位移;(2-3){i,m},{j,n}指定点的索引i和j的取值范围分别为1到m和1到n。中间一层是Flatten(展平)函数,用来将其第一个参数即最内一层Table函数产生的二维列表展平为一维列表,它的第二个参数指定展平层数为1。最外一层是ListPlot函数,用来生成声波之行波的一个静态图,该函数包含四个参数:(1)PlotRange→{{-1,6π+1},{-1.25,1.25}}指定横纵坐标轴的显示范围分别是[-1,6π+1]和[-1.25,1.25];(2)PlotMarkers→{Automatic,Tiny}使用默认的、微小的形状来绘制点的标记;(3)PlotStyle→Black指定绘图颜色为黑色;(4)Axes→False用来隐藏图中的坐标轴。
第二步使用Table函数产生一系列循序渐进的静态图(images)。这里的Table函数有两个参数:(1)image[t];(2){t,0,2π,2π/180}用来指定目标函数中自变量t的取值列表,其起始值为0,终止值为2π,步长为2π/180。第三步运用Export函数将系列静态图images按顺序合成并输出为一个动态图,它有五个参数:(1)“声波之行波.gif”是输出文件的名字;(2)images;(3)“DisplayDurations”→0.05指定动态图中每帧图像的显示时间为0.05秒;(4)ImageSize→{720,360}指定动态图中每帧图像的横轴像素数和纵轴像素数为720和360;(5)“AnimationRepetitions”→6指定动画重复播放次数为6。
根据波动公式(2),将上段程序代码中的A*Cos[ω*t-k*x0[i]+φ]替换为A*Cos[ω*t+k*x0[i]+φ1]+A*Cos[ω*t-k*x0[i]+φ2],并令A=0.5,即可得到声波的驻波的动态效果图,如支持信息中动态图S1(b)所示。因文章中不能展示动态图,本节仅在图2中展示声波的行波在一个周期内四种状态的静态图。从支持信息中动态图S1(a)和图2可以看出,行波是在向右“行走”的,而根据支持信息中动态图S1(b),驻波并不“行走”,只是在波腹和波节之间往复运动。

图2 声波的行波
2 简谐水波
水波是一种复杂类型的机械波,在其强度较小、波长较短时,可以近似看成沿平面传播的简谐波。生活中观察到的水波,受限于观测条件和视角,无法看到水波完整的运动状态。为此,本研究通过Mathematica绘制出多种视角的简谐水波三维动态图,以供学习者形象地认识和理解水波的运动。简谐水波的波动公式为
(3)
基于波动公式(3),在Mathematica中输入并执行如下语句
A=1;ω=1;k=1;φ=0;

RegionFunction→Function[{x,y},x2+y2<(4π)2],
PlotStyle→Hue[0.58,0.56,0.73],
Boxed→False,Axes→None,Mesh→None];
images=Table[image[t],{t,0,2π,2π/180}];
Export[“水波(45度俯视).gif”,images,“DisplayDurations”→0.05,
ImageSize→{720,360},“Animation Repetitions”→6]
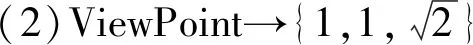
因文章中不能展示动态图,本节仅在图3中展示三张t=2π时刻的静态图。从支持信息中动态图S2(a)~(b)以及图3(a)和(b)可以看出,水波是一圈一圈向外传播的,同时从支持信息中动态图S2(c)以及图3(c)可以明显看到余弦函数图像,这是由简谐水波满足的波动公式决定的。

图3 简谐水波在多视角下的三维图像
3 通过单缝和双缝的光波
无论是在教科书上,还是在实验中,学生们观察到的只是通过单缝或双缝的光波呈现在光屏上的条纹。为了更完整地呈现光波形态,作为示例,本节通过Mathematica中的DensityPlot函数绘制了通过无限窄单缝和双缝的光波在传播空间中的强度分布图像。这里所谓的“无限窄”是当单缝和双缝宽度在理论上足够窄以致光的衍射现象可以忽略时的一种理想近似。在Mathematica中,DensityPlot函数可用颜色的明暗表达强度的大小;而在光学现象中,强度的大小又表现为颜色的明暗。因此,DensityPlot函数是实施该部分动态模拟的理想工具。作图时使用的通过单缝和双缝的光波的强度公式分别为
(4)
(5)
这里,单缝与xy平面垂直相交于(0,0)点,双缝与xy平面分别垂直相交于(x1,y1)点和(x2,y2)点。
基于光强公式(4),在Mathematica中输入并执行如下语句
A=1;B=1;x1=0;x2=0;y1=-5π;y2=5π;
ω=1;k=1;φ=0;φ1=0;φ2=0;λ=589.3;

ColorFunction→(Hue[0.7Cos[(λ-400)/170]2,1,#]&),
Frame→None,PlotPoints→100];
images=Table[image[t],{t,0,2π,2π/10}];
Export[“通过单缝的光波.gif”,images,“DisplayDurations”→0.025,
ImageSize→{720,720},“Animation Repetitions”→6]
即可得到通过单缝的光波在传播空间中的强度分布图像的动态效果图,如支持信息中动态图S3(a)所示。在此image函数的定义中,DensityPlot函数包含六个参数,上文未介绍过的参数如下:(1)ColorFunction→(Hue[0.7Cos[(λ-400)/ 170]2,1,#]&)通过Hue函数配置ColorFunction参数实现对光波颜色的精确模拟,程序开头已指定波长λ=589.3,表示将光波设置为钠灯发出的黄光,更改波长λ的数值可以得到对不同波长光波的精确仿真;(2)Frame→None用来隐藏默认的图像边框。

(a) 通过单缝的光波
4 平面电磁波
平面电磁波是麦克斯韦方程组的基础特解,是交变电磁场的基本形式,清楚地知晓平面电磁波的传播图像对于理解电磁波理论具有极其重要的意义。具体而言,平面电磁波是相互垂直且同频同相振荡的电场与磁场在空间中的传播,其电场和磁场分量可以分别表达为
E(z,t)=E0cos(ωt±kz+φ) ,
(6)
B(z,t)=B0cos(ωt±kz+φ) ,
(7)
关于平面电磁波的图像,我们通常看到的都是静态图片,为了让学习者看到更加生动的图像,本研究使用Mathematica中的三维作图函数Graphics3D和ParametricPlot3D绘制了平面电磁波传播的动态效果图。
基于公式(6)和(7),在Mathematica中输入并执行如下语句
E0=π;B0=π;ω=1;k=1;φ=0;n=2;
Emin=-1.25E0;Emax=1.25E0;Bmin=-1.375B0;Bmax=1.375B0;
zmin=-0.5π;zmax=4.25π;

Text[Style[″E″,16,Black,Bold],{0.95*zmax,0,0.2*zmin}],
Text[Style[″B″,16,Black,Bold],{0.1*Emax,0,0.2*zmin}],
Text[Style[″z″,16,Black,Bold],{0,0.2*Bmax,zmax}],
Green,Thick,Arrowheads[0.02],Arrow[{{0,Bmin,0},{0,Bmax,0}}],
Green,Thick,Arrowheads[0.02],Arrow[{{0,0,zmin},{0,0,zmax}}],
Green,Thick,Arrowheads[0.02],Arrow[{{Emin,0,0},{Emax,0,0}}],
Table[{Thin,Lighter[Red,0.2],Line[{{0,0,z},
{E0*Cos[ω*t-k*z+φ],0,z}}]},{z,0,n*2π,n*2π/100}],
Table[{Thin,Lighter[Blue,0.2],Line[{{0,0,z},
{0,B0*Cos[ω*t-k*z+φ],z}}]},{z,0,n*2π,n*2π/100}]},
PlotRange→{{Emin,Emax},{Bmin,Bmax},{zmin,zmax}},
PlotLabel→Row[{Style[“-电场分量”,20,Red,Bold],“ ”,
Style[“-磁场分量”,20,Blue,Bold]}],ViewVertical→{1,0,0},ViewPoint→{6,2,2},
Boxed→Flase,Axes→True,Ticks→None,
AxesOrigin→{0,0,0},AxesStyle→Black],
ParametricPlot3D[
{E0*Cos[ω*t-k*z+φ],0,y},{z,0,n*2π},PlotStyle→{Red,Thick}],
ParametricPlot3D[
{0,B0*Cos[ω*t-k*z+φ],z},{z,0,n*2π},PlotStyle→{Blue,Thick}]];
images=Table[image[t],{t,2π/100,2π,2π/100}];
Export[“平面电磁波.gif”,images,“DisplayDuartions”→0.05,
ImageSize→{720,540},“Animation Repetitions”→6]
即可得到平面电磁波传播的三维动态效果图,如支持信息动态图S4所示。在此image函数的定义中,Show(显示)函数用来同时显示多个由不同绘图函数生成的图像,在这段代码中它有三个参数:(1)Graphics3D函数整体,用来绘制坐标轴相关组件和电磁波电场与磁场分量的振动矢量(省略矢量箭头);(2-3)两个ParametricPlot3D函数整体,分别用来绘制电磁波的电场与磁场分量的波动曲线。其中,Graphics3D函数中的核心元素是运用Table函数、Line函数以及E0*Cos[ω*t-k*z+φ]和B0*Cos[ω*t-k*z+φ]目标函数绘制电磁波的电场与磁场分量的振动矢量。两个ParametricPlot3D函数各自包含三个参数:(1){E0*Cos[ω*t-k*z+φ],0,y}和{0,B0*Cos[ω*t-k*z+φ],z}分别用来指定电场和磁场波动曲线上点的坐标;(2){z,0,n*2π}指定图像中电磁波的传播范围;(3)PlotStyle→{Red,Thick}和PlotStyle→{Blue,Thick}分别指定用蓝色和红色的粗线来绘制电场和磁场波动曲线。
从支持信息中动态图S4可以看到平面电磁波传播的清晰图像:电场分量和磁场分量同频同相、相互垂直,且沿着与它们都垂直的方向传播。因文章中不能展示动态图,本文仅在图5中展示其在t=2π时刻的静态图。
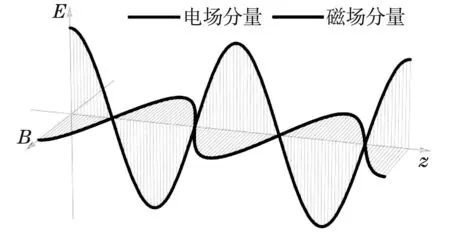
图5 平面电磁波的传播
5 结 论
本文基于Mathematica这一功能强大、用法简单、语法优雅的数学软件,动态模拟了物理学中多种典型的波动现象,其中包括:(1)声波的行波和驻波;(2)简谐水波在多视角下的三维图像;(3)通过单缝和双缝的光波在传播空间中的强度分布图像;(4)平面电磁波的传播。经过不断地学习、探索与实践,基于相关波动公式,本研究绘制出了以上各种波动现象的动态效果图。这些动画准确、直观、形象,非常有助于学习者建立清晰的物理图像,增加对上述波动现象的认识,增进对相应波动规律的理解,为物理课程增添了丰富多彩的教学资源。
本文以经典物理学中波动现象的动态模拟为例介绍了基于Mathematica的物理教学资源开发,涉及的波动公式比较简洁,相应的物理图像也较简单。然而,波动现象不仅是经典物理学的研究对象,考虑到波粒二象性,波动力学也是量子力学的主要表现形式之一。相比于经典物理学中的波动公式,量子力学中的波函数更加复杂,相关的物理图像更难想象。目前已有不少文献对量子力学中的波函数进行可视化研究[11-15],但这些研究主要集中在静态可视化方面,鉴于波函数会随时间演化,对其进行动态可视化研究,也具有重要意义,可以作为将来进行物理教学资源开发的一个拓展方向。
此外,本文充分展示了Mathematica软件强大的图形绘制功能和便捷的动画合成功能,反映了其在物理教学资源开发方面的广阔应用前景。鉴于Mathematica软件易于学习和使用,教师可以将相关知识、技能、方法和经验讲授给感兴趣的学生,使其能够面向自身学习过程中的疑难和困惑,和教师一起进行相关的物理教学资源开发。在此师生互动的教学研究实践过程中,学生能够深化对知识的理解,增强解决问题的能力,体会思考和探索的乐趣,为其成长为创新型人才奠定基础。
本文支持信息下载网址:http://dawushiyan.jlict.edu.cn/CN/10.14139/j.cnki.cn22-1228.2024.01.018
