TEB算法参数对智能车路径规划的影响仿真分析
2024-01-11廖兴华甘桦福柳皓凯
廖兴华 甘桦福 柳皓凯
摘 要:本文针对智能车在室内环境的路径规划,分析研究了TEB算法不同参数对智能小车的路径规划影响。仿真结果表明,5大参数中有部分关键参数对智能小车的路径规划生成影响重大。需要设置最优的值才能最终获得一条时间最短、距离最短、避开障碍物的最优路径。才能让智能小车进行路径规划并跟踪路径顺利到达目标点。
关键词:路径规划 TEB算法 智能车
1 引言
随着科学技术的发展,无人驾驶技术已经不是遥不可及,随着智能车走进我们日常生活,为我们提供了极大的便利。如扫地机器人的应用减轻了家务劳动。疫情期间无人送货车也发挥了巨大的作用。部分发达城市开展的无人驾驶汽车乘坐体验等。都预示着智能车技术的发展越来越成熟。而作为智能车的核心技术,路径规划和路径跟踪算法决定着智能车能否正常运行的关键。因此对算法的研究已经成为当前研究者的热点问题。本文以TEB算法为例,研究TEB算法中的参数对智能车路径规划生成和跟踪的影响。
2 路径规划算法介绍
路径规划是指在一定的环境模型基础上,给定无人驾驶汽车或智能网联汽车起始点和目标点后,按照性能指标规划出一条无碰撞、能安全到达目标点的有效路径[1]。
智能车常用的路径规划算法有A*算法,Dijkstra算法,TEB(Time Elastic Band)算法,DWA(Dynamic Window Approach)算法等。不同算法都有自己的特点。A*算法的核心部分是它对每个道路节点均设计了一个估价函数,为了保证搜索路径的最优性,通常选择启发函数h(s)为曼哈顿距离、欧几里得距离。A*算法用于规划路径缺点是拐点多、不平滑,不利于机器人的运行[2]。
Dijkstra算法核心思想是设置两个节点的集合C和O,集合C中存放已找到最短路径的节点,集合O存放当前还未找到最短路径的节点。初始状态时,集合C中只包含起始点,然后不断从集合O中选择到起始节点路径长度最短的节点加人集合C中。集合C中每加入一个新的节点,都要修改从起始点到集合O中剩余节点的当前最短路径长度值,集合O中各节点新的前最短路径长度值为原来最短路径长度值与从起始点经过新加入节点到达该节点的路径度中的较小者。不断重复此过程,直到集合O中所有结点全部加入集合C中为止[1]。
Dijkstra算法是一种贪心算法,每一步都选择局部最优解,以期望产生一个最优解。缺点是该算法执行时间长,算法较复杂,速度较慢,很难满足路径规划的实时性要求[3]。
DWA(Dynamic Window Approach)动态窗口法,动态窗口算法是由 Dieter Fox[4]等于1997年基于曲率速度思想提出的一种局部路径规划方法,考虑到运动速度、载体的运动方向和到最近障碍物的距离3个方面,通过离散搜索空间进行优化。该算法只适合全向运动机器人和差速运动机器人[5]。虽然学者们都根据需要针对特定的环境采用了不同的算法,改进了算法。但是很少有学者提出算法中设置的参数对路径规划的影响。基于以上问题,本文以TEB算法为例,研究TEB算法中的参数对智能车路径规划生成和跟踪的影响。
3 TEB算法原理
TEB(Time Elastic Band)算法俗称橡皮筋算法。连接起始、目标点,并让这个路径可以变形,变形的条件就是将所有约束当做橡皮筋的外力。中间插入N个控制橡皮筋形状的控制点,点与点之间定义运动时间time[6]-[7]。非常适合阿克曼转向车型。它的特点是[8]:
1.控制量是车速和前轮转角。
2.约束条件是:
(1)路径跟踪和避障。路径跟踪将运动物体拉向全局路径,避障又推出全局路径。(2)速度和加速度要在最大值和最小值之间。
经过上面的目标函数的约束,然后使用开源的G2O库(General Graph Optimization通用图优化法)进行优化,发送速度指令。最终获得一条时间最短、距离最短、避开障碍物且尽可能跟踪全局路径的局部路径。
基于TEB算法的以上特点,本文采用TEB算法在仿真环境中研究算法参数对阿克曼转向的智能小车路径规划的影响。
4 仿真环境搭建
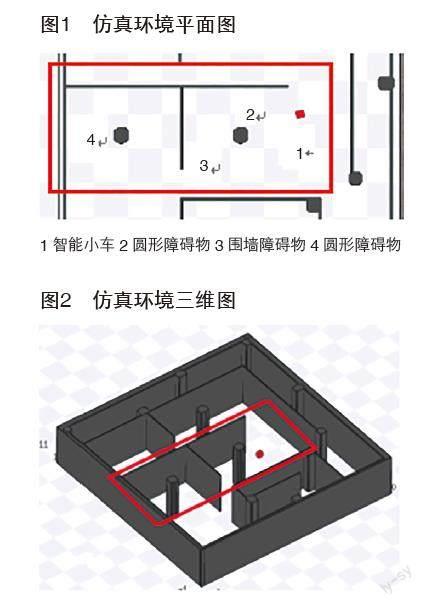
仿真环境地图是让智能小车1通过3个障碍物,其中两个圆形障碍物2和4,一个围墙障碍物3,如图1和图2所示,考察不同参数对小车的影响。
4.1 TEB算法的参数影响分析
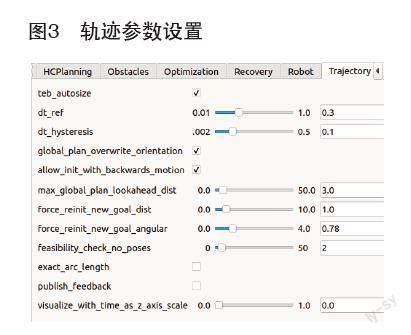
TEB算法有5大参数,分别是[9]:Trajectory(轨迹)、robot(智能小车)、GoalTolerance(目标容忍度)、Obstacles(障碍物)、Optimization(优化)。每个参数包括一系列子参数如图3所示,列出了轨迹参数的子参数。
其中Trajectory关键参数包括dt_ref:含义是局部路径规划的解析度,即两个相邻点位姿时间的分辨率[10]。保持默认设置0.3。设置过小会导致小车计算量大,速度很慢,如果设置过大导致仿真时小车无法通过转弯处并严重偏離规划轨迹。如图4所示分别设置为0.3和1的路径规划效果。
max_global_plan_lookahead_dist含义是考虑优化的全局计划子集的最大长度。决定局部规划初始轨迹的最大长度,由于局部轨迹在每个控制周期都被更新,实际执行的指令仅是轨迹上第一个点的速度值,保持默认3即可。
智能小车robot参数设置包括max_vel_x,最大x前向速度,max_vel_y,最大y前向速度,和max_vel_theta,最大转向角速度等。如图5所示。
其中,max_vel_x,x前向最大速度根据实际小车性能进行设置,默认是0.4m/s。如何设置太大会导致偏离路径规划的路线。如图6所示绿框中绿线是原定规划路径,红线是重新规划路线,设置5m/s后导致转弯时偏离轨迹。
由于仿真的小车是阿克曼转向车型,所以参数max_vel_y设置为0。参数min_turning_radius(最小转弯半径)针对阿克曼车型根据实际设置,如果是全向移动小车设置为0。
GoalTolerance(目标容忍度)参数包括xy_goal_tolerance(目标x和y方向的偏移容忍度值),yaw_goal_tolerance(目标角度偏移容忍度),free_goal_vel(允许机器人以最大速度驶向目的地)三个参数。如图7所示。
xy_goal_tolerance,值设置多少就表示小车距离目标点在这个值范围内就代表达到目的地。默认是0.2m。如果设置太小如0.001,那么小车将在目标的附近往复很多次,直到达到设定的值,浪费很多时间,如图8所示绿框处。同理yaw_goal_tolerance默认也是0.2弧度。free_goal_vel默认是false。
Obstacles(障碍物)参数用于设置环境地图中对障碍物的处理,关键参数包括min_obstacle_dist(和障碍物的最小距离),include_costmap_obstacles(是否将动态障碍物预测为速度模型),costmap_obstacles_behind_robot_dist限制机器人后方规划时考虑的局部成本地图障碍物。如图9所示。
其中,min_obstacle_dist和障碍物的最小安全距离根据需要设置,设置太大会导致小车无法通过狭小的地方。一般设置0.2m即可。include_costmap_obstacles默认是true,只有真时,小车才在行驶过程中规避实时探测到的建图时不存在的动态障碍物。 costmap_obstacles_behind_robot_dist小车在行驶途中会考虑后方障碍物与自身的安全距离值。默认是1米。
optimization(优化)参数关键参数包括no_inner_iterations(被外循环调用后内循环执行优化次数),no_outer_iterations(执行的外循环的优化次数),penalty_epsilon(对于硬约束近似在惩罚函数中添加安全范围),weight_kinematics_forward_drive(优化过程中,只让机器人选择前进方向),weight_kinematics_turning_radius(优化过程中,最小转弯半径的权重)。如图10所示。
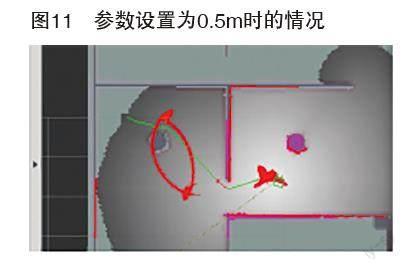
其中,no_inner_iterations和no_outer_iterations保持默认设置为5和4。penalty_epsilon参数意义为小车快到达目标点时提前减速的缓冲值,为了安全起见,该值越小越好。一般设置为0.1m。如设置过大导致小车不能按照原规划路径行驶,出现卡死现象,如图 11所示设置为0.5m,小车卡住不动,不停重新规划路径。weight_kinematics_forward_drive参数是用于抑制小车倒车的,数值越大,则小车倒车机率越小,避免小车频繁倒车。但是不能完全抑制倒车情况发生。weight_kinematics_turning_radius参数设置越大越容易达到小车的最小转弯半径,但是过大也会导致小车不停地重新规划路径,默认是1m。
5 总结
本文通过对TEB算法的5大参数的调试仿真,分析研究了不同参数对智能小车的路径规划影响。仿真发现Trajectory(轨迹)的关键影响参数是dt_ref和max_global_plan_lookahead_dist;robot(智能小车)关键影响参数是max_vel_x,min_turning_radius;GoalTolerance(目标容忍度)关键参数是xy_goal_tolerance; Obstacles(障碍物)关键参数是min_obstacle_dist、include_costmap_obstacles、costmap_obstacles_behind_robot_dist;Optimization(优化)的关键参数是penalty_epsilon、weight_kinematics_forward_drive、weight_kinematics_turning_radius。他们之间互相作用共同影响着智能车的路径规划实现。
基金项目:柳州铁道职业技术学院资助研究。
参考文献:
[1]陈慧妍,熊光明,龚建伟等.无人驾驶汽车概论[M] 北京理工大学出版社,2018.5.
[2]陈劲宇.DWA算法和VO混合路径规划算法对比研究[J].吉林大学学报(信息科学版)2022.11第40卷第6期.
[3]陈慧妍,熊光明,龚建伟.无人驾驶车辆理论与设计[M] 北京理工大学出版社,2018.3.
[4]海振洋,王健,牟思凯等.无人驾驶路径规划算法综述[J]. 农业装备与车辆工程.2022.11第60卷第11期.
[5]代婉玉. 改进TEB算法的局部路径规划算法研究[J].计算机工程与应用.2022,58(8).
[6]高胜寒.智能车辆路径规划算法研究与仿真[D].哈尔滨:东北林业大学,2022.
[7]cabinx.Timed-Elastic-Band局部路徑规划算法[EB/OL].https://blog.csdn.net/xiekaikaibing/article/details/83417223.
[8]盖军雄,雷晓春,江泽涛.基于 ROS 的阿克曼机器人室内导航实现[J].中国体视学与图像分析. 2021 年 第 26 卷 第 3 期.
[9]zhenz1996.TEB轨迹优化算法-代码解析与参数建议[EB/OL].https://blog.csdn.net/zz123456zzss/article/details/104692548.
[10] ROS.[EB/OL].http://wiki.ros.org/teb_local_planner#Parameters.
