基于滑模变结构的农机路径跟踪控制算法研究

姜龙腾,迟瑞娟,李青君,黄修炼,熊泽鑫,马悦琦,朱晓龙

(1.中国农业大学 工学院,北京 100083; 2.上海海事大学 商船学院,上海 201306)

0 引言

农机自动驾驶是实现农业机械现代化必不可少的一环,农机自动驾驶的路径规划及路径跟踪是研究农机无人驾驶技术的基础和关键[1]。路径跟踪的目的是通过跟踪算法使车辆按照预定路径轨迹行驶,主要工作模式是通过车载传感器获取当前车辆姿态及位置信息,根据创建的车辆运动学模型,通过上位机计算出车辆控制参数,从而保证车辆行驶轨迹与预设轨迹路径误差最小化[2-3]。

目前,路径跟踪算法有纯跟踪控制算法[4]、PID控制算法[5]、神经网络[6]、滑模变结构法、机器学习[7]以及前轮反馈控制算法[8]等。对于滑模变结构法的控制算法,许多学者也进行过大量研究。1978年,Young等人首先将滑模变结构控制器应用于机器人的控制中[9]。2004年,王荣本等人采用滑模变结构控制理论设计了控制器,并建立了汽车转向动力学模型,采用二次型最优设计法搭建了系统的切换超平面,并描述了切换超平面的一些选取方法,经过试验测试后,车辆具有良好的跟踪效果[10]。2013年,Guo J H 等人提出了一种横向自适应的模糊滑模控制方法[11],能够克服预瞄运动学模型中的参数不确定问题,与单纯的滑模控制相比,这种方法有利于提高汽车跟随过程中的跟踪精度,且响应时间较短,反应灵敏。

农机与汽车或机器人工作性质不同,其需要克服较为复杂的农田环境因素干扰,同时障碍物的存在会对算法修正参数产生影响[12],故选择合理的路径跟踪算法将提升农机的作业效率、改善农艺水平。为满足农机行驶的平顺性、安全性及控制精度要求,本文采取滑模变结构路径跟踪控制算法设计路径跟踪控制器,建立汽车运动学模型,并通过Simulink与CarSim进行联合仿真分析,对比分析基于PID控制算法的预瞄时间自适应模块的路径跟踪效果,以验证滑模变结构路径跟踪控制效果的理想性。

1 车辆的运动学模型

由于农田环境较为复杂,道路较为崎岖,本文采用二轮车辆模型来分析无人驾驶农机的运动情况。假设汽车始终做平行于地面的运动,速度向前为正,向后为负。车辆的运动学模型如图1所示。

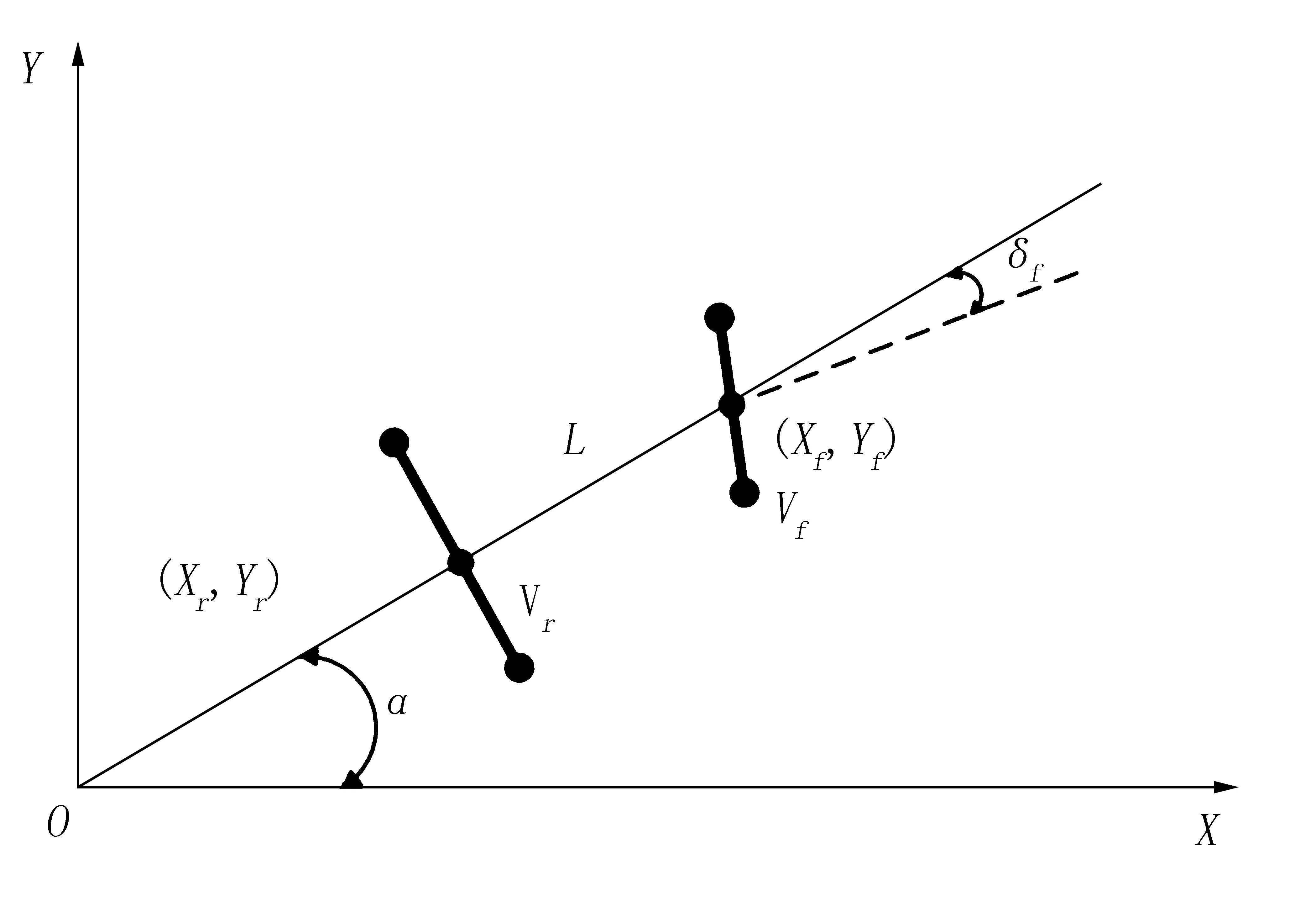
图1 车辆的运动学模型Fig.1 Kinematics model of the vehicle

以xoy为坐标系,x为汽车的横向位置,y为汽车的纵向位置,(xf,yf)为汽车前轴坐标,(xr,yr)为汽车后轴坐标,vf为汽车前轴中心的速度,vr为汽车后轴中心的速度,δf为汽车前轮转角。图1中,l为汽车前后轴距,α为汽车的航向偏角[13]。

根据车辆的运动学模型,可以得到

(1)

(2)

(3)

vr=vfcosδf

(4)

将式(1)～式(4)整理化简可以得到汽车前进和后退的运动学模型,即

(5)

(6)

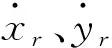
(7)

2 基于滑模变结构路径跟踪控制器设计

经典的PID控制算法虽然应用较广,技术较为成熟,但由于其对环境适应性较差,导致其跟踪精度不高。因此,设计了一种滑模变结构控制器应用于无人驾驶农机的轨迹跟踪,该算法具有对环境适应性好、抗干扰能力强等优点。

2.1 转向控制策略

滑模变结构控制器采用的转向控制策略为:将方向盘转角信号和农机上安装的各类传感器所感知的状态信号输入到农机的状态观测器,从而获得与农机稳定性相关的数值。将该数值与理想值输入到控制器中[14],经过上位机计算出的转角理想值与车载传感器输出的实际值产生一个偏差,利用该偏差来控制转向电机,电机产生一个叠加转角,该叠加转角与模拟驾驶员输入的方向盘转角之和即为农机行驶过程中总的方向盘转角,从而使农机行驶更加稳定。转向控制策略如图2所示。

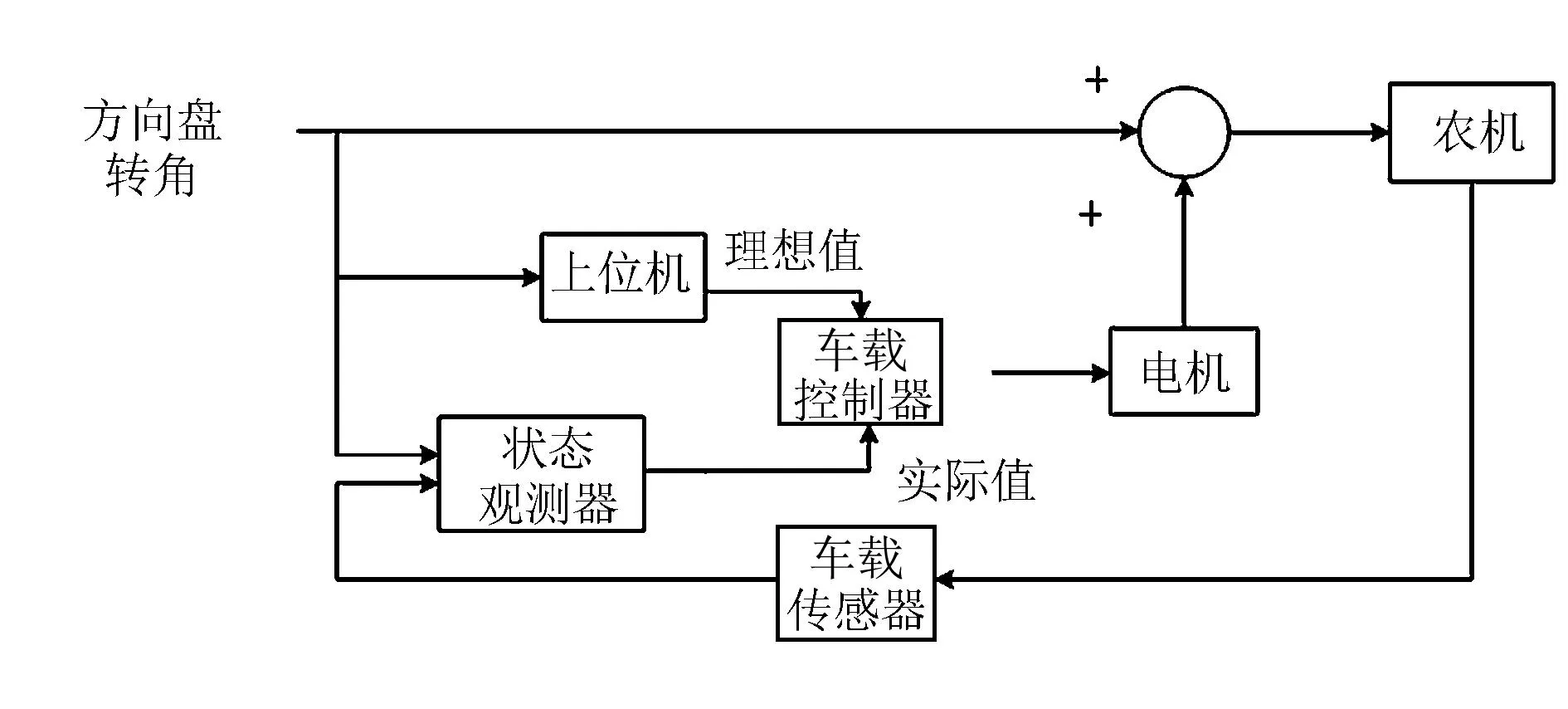
图2 转向控制策略框图Fig.2 Block diagram of steering control strategy

农机在行驶过程中,当其转向输入后会产生质心侧偏角和横摆角速度等响应,这些响应与转向输入符合线性关系,可构建该线性二自由度车辆模型为

(8)

(9)

(10)

其中,δf为前轮转角;k1为前轮的侧偏刚度;k2为后轮的侧偏刚度;x=[β,ωd]T为车辆的状态变量;β为质心侧偏角;ωd为横摆角速度。

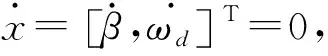
(11)

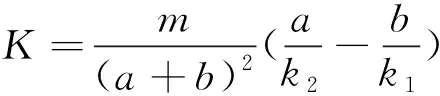
(12)

其中,μ为路面的附着系数。

2.2 滑模变结构控制器设计

根据简化农机车辆模型与线性化运动学方程,可以得到实际的横摆角速度与理想的横摆角速度之差为滑模变结构控制器的控制误差,公式为

e=ωr-ωd

(13)

其中,ωr为实际的横摆角速度;ωd为理想的横摆角速度。

理想的横摆角速度选择为

(14)

其中,LH为汽车的预瞄距离,tp定为0.6s。

滑模变结构的切换函数定义为

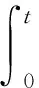
(15)

其中,λ0为加权系数,其数值为正。

式(15)进行求导可得

(16)

由式(8)可得

(17)

然后,再将式(16)代入式(17),可得

(18)

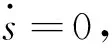
(19)

为了保证滑模变结构控制器的滑模条件可以不受系统干扰和参数变化的影响,定义滑模控制规律为

δf=δf_equ-k0sgn(s)

(20)

其中,sgn(s)为符号函数;k0为系统的工作点趋近于切换面的运动速率,其数值越大趋近速度越快。因当k0值过大时系统产生的抖动较大,故其数值的选取应满足如下条件,即

(21)

其中,η0为正实数。

为了消除控制输入所产生的振动,将符号函数sgn(·)用饱和函数sat(·)进行代替,公式为

(22)

所以,最终滑模变结构控制器的控制规律为

δf=δf_equ-k0sat(s/ε)

(23)

其中,ε为边界层的宽度。

3 路径跟踪控制算法的联合仿真分析

3.1 基于预瞄时间自适应PID的路径跟踪控制仿真分析

3.1.1 Simulink模型的建立

在PID控制算法的基础上加入了预瞄时间自适应模块,通过Simulink建立可以输出一个自适应预瞄时间,其与速度之积为自适应预瞄距离。将自适应预瞄距离作为CarSim的输入,使车辆仿真过程中能够获得最佳预瞄距离,提高其跟踪精度[15]。

首先,根据PID控制算法的规则建立Simulink模型,如图3所示。经过多次调试,最终确定比例部分Kp的数值为100,积分部分Ki的数值为15,微分部分Kd的数值为1.5。

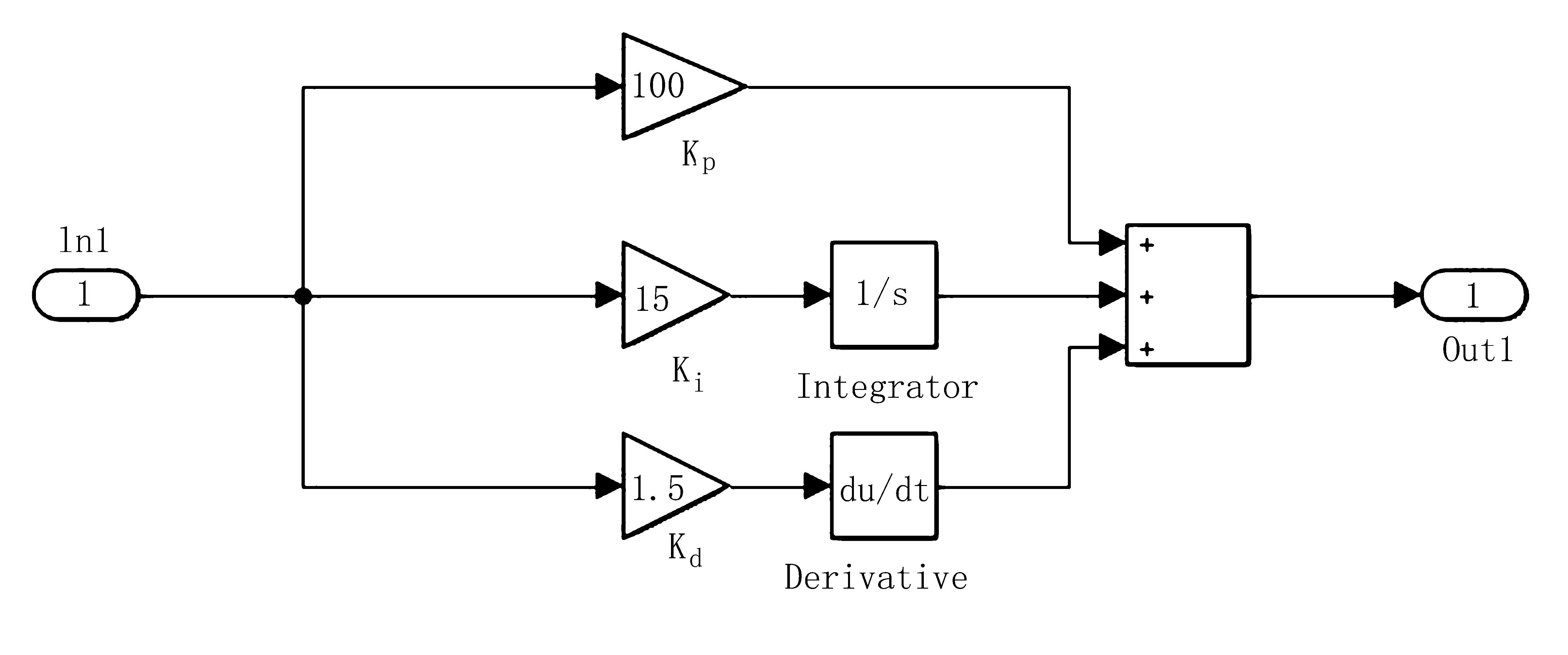
图3 PID模块的Simulink模型Fig.3 Simulink model of PID module

然后,根据预瞄时间自适应控制规律建立预瞄时间自适应控制器的Simulink模型,如图4所示。

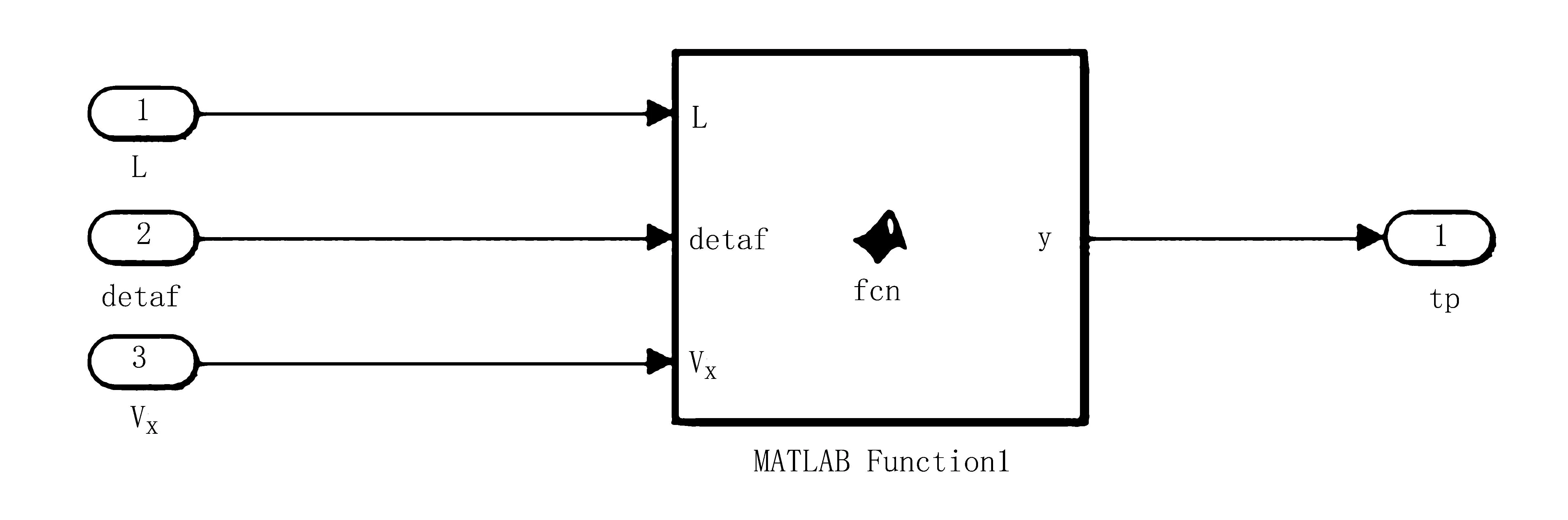
图4 预瞄时间自适应控制器的Simulink模型Fig.4 Simulink model of adaptive controller for preview time

图4中,L为质心的横向偏差;detaf为车辆的航向角偏差;Vx为车速;tp为自适应预瞄时间。

预瞄时间自适应模块的整体Simulink模型如图5所示。

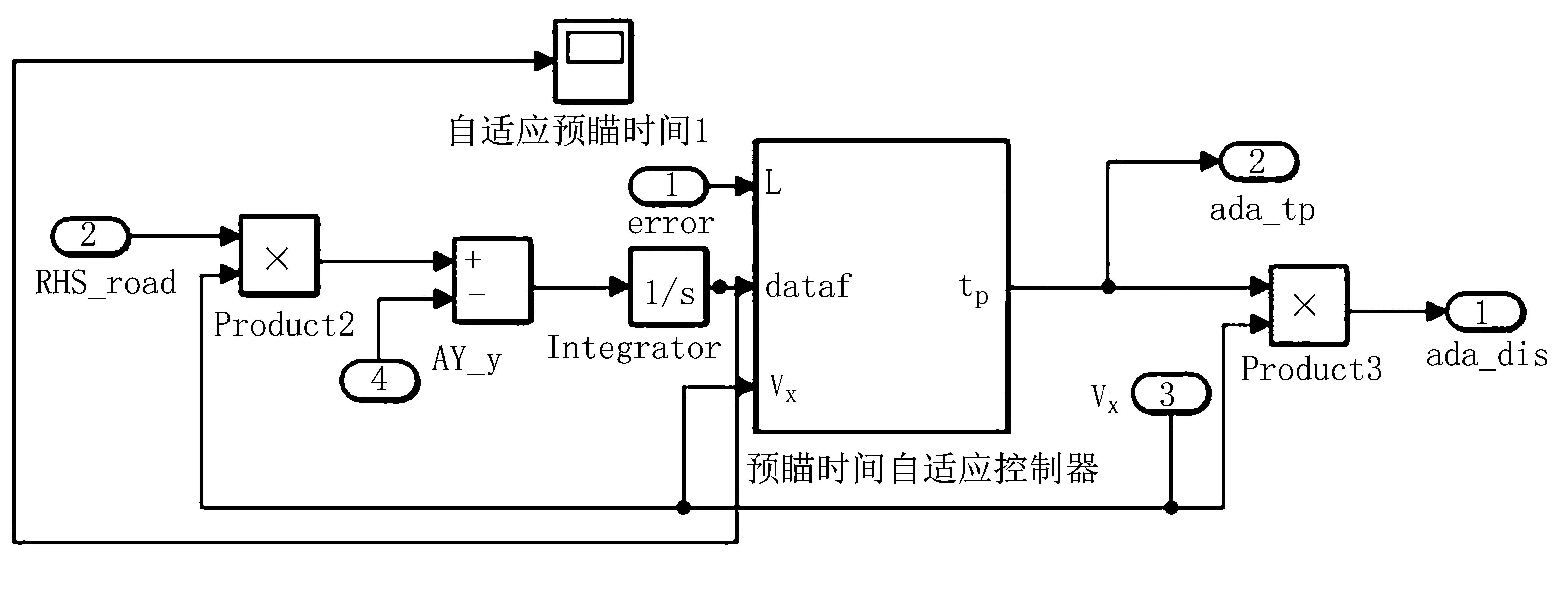
图5 预瞄时间自适应模块的Simulink模型Fig.5 Simulink model of adaptive module of preview time

图5中,RHS_road为道路的曲率;AY_y为汽车行驶时的加速度;ada_tp为自适应预瞄时间;ada_dis为自适应预瞄距离,即自适应预瞄时间与汽车行驶速度之积。

3.1.2 CarSim模型的建立

在CarSim中搭建汽车的整车模型以及道路模型,输入农机车辆参数,并设置道路图形,如图6所示。

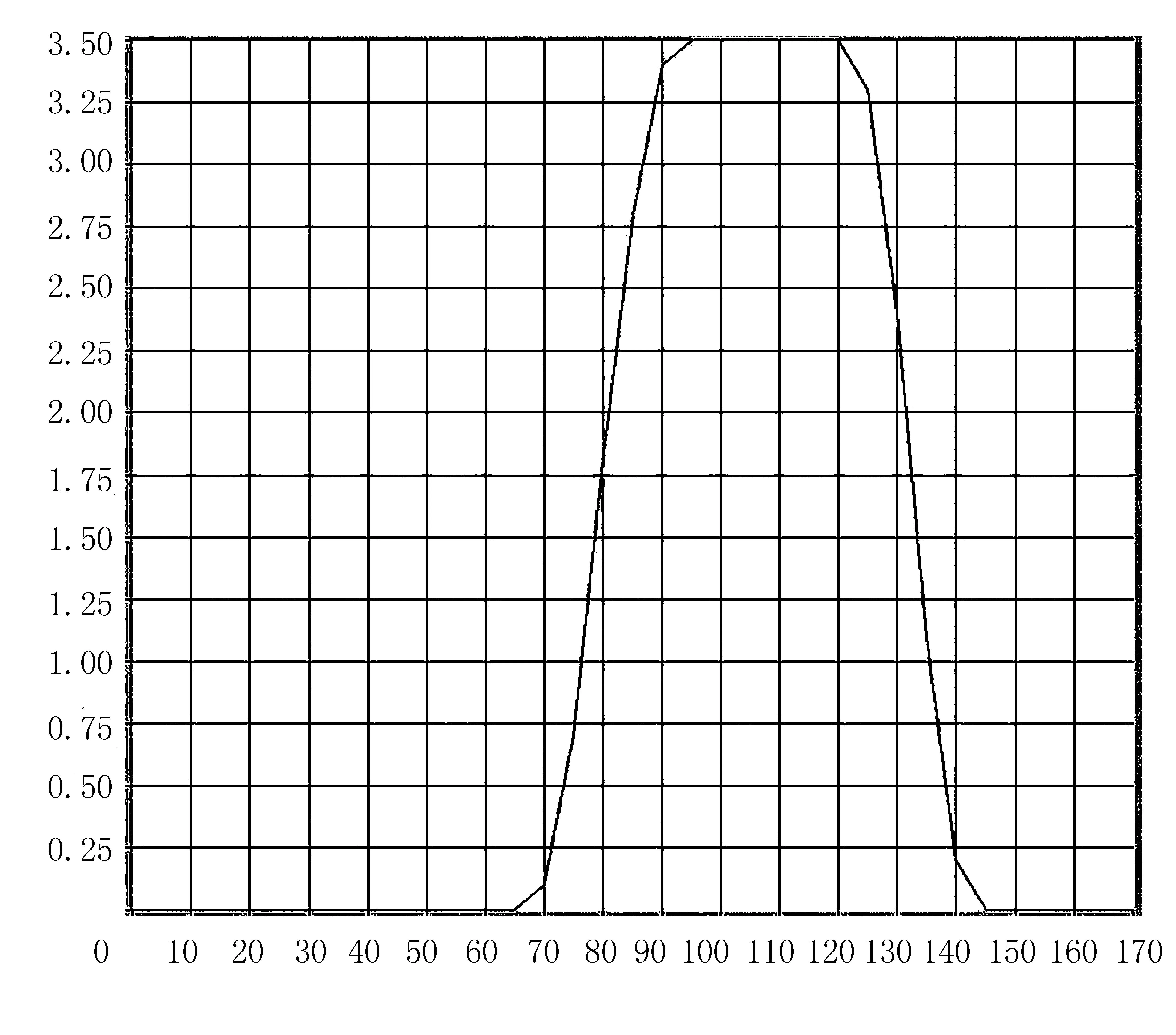
图6 PID算法的CarSim道路图形Fig.6 CarSim road graph of PID algorithm

然后,设置CarSim整车模型的输入与输出。其中,自适应的预瞄距离和方向盘转角为CarSim的输入,质心横向偏差、曲率、纵向车速、加速度、质心侧偏角、预瞄点的横向偏差、实际位置、理想位置为CarSim的输出。

在CarSim中选择“Send to Simulink”,进行联合仿真分析,结果如图7所示。

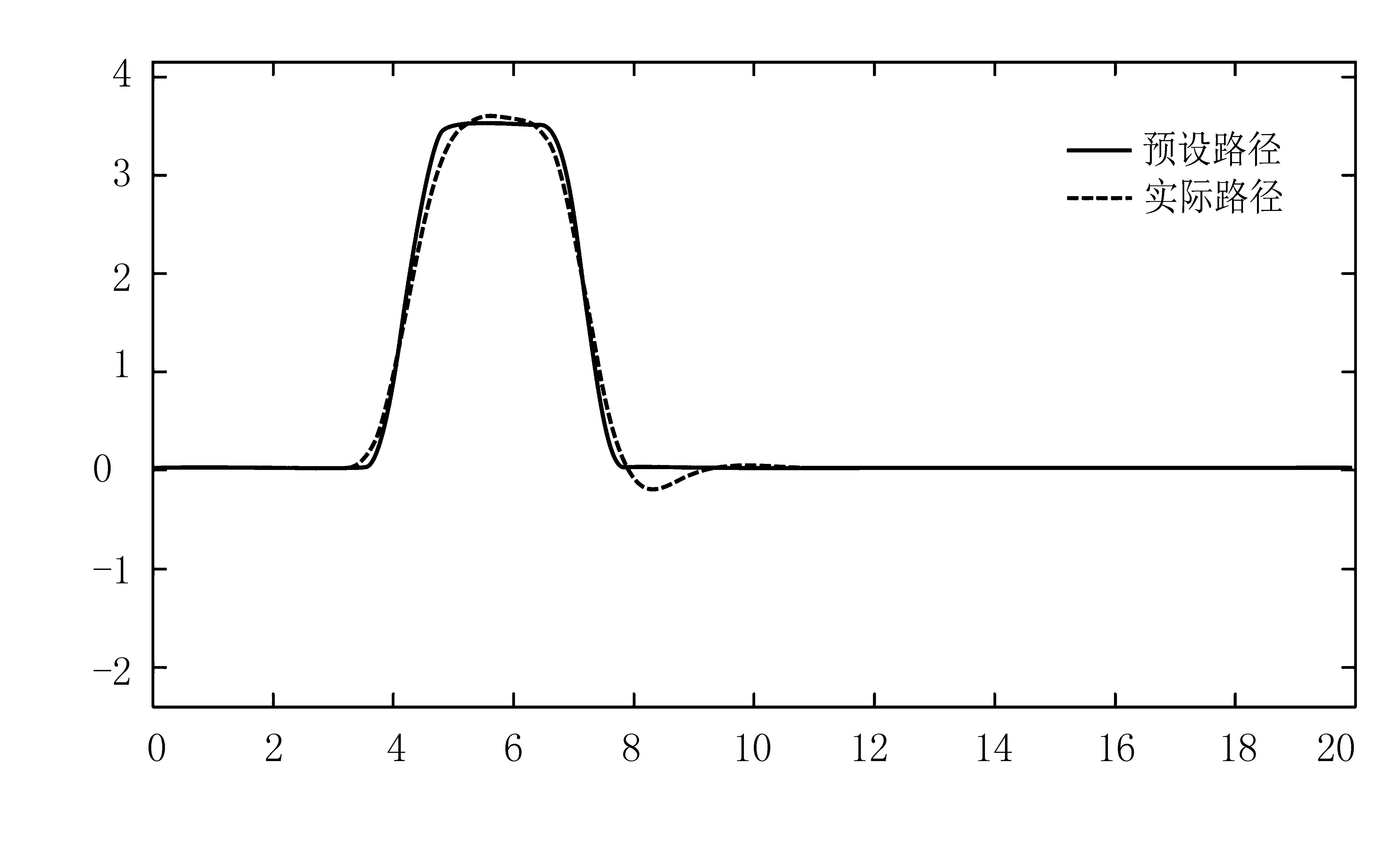
图7 实际路径与参考路径对比图Fig.7 Comparison between actual path and reference path

质心侧偏角如图8所示。由图8可知:加入预瞄模块的PID控制算法虽然简单,但是其本身对环境的变化比较敏感,质心侧偏角受转向影响较大,最大质心侧偏角在0.15°左右,抗干扰能力差以及超调量较大,其跟踪效果并不理想。

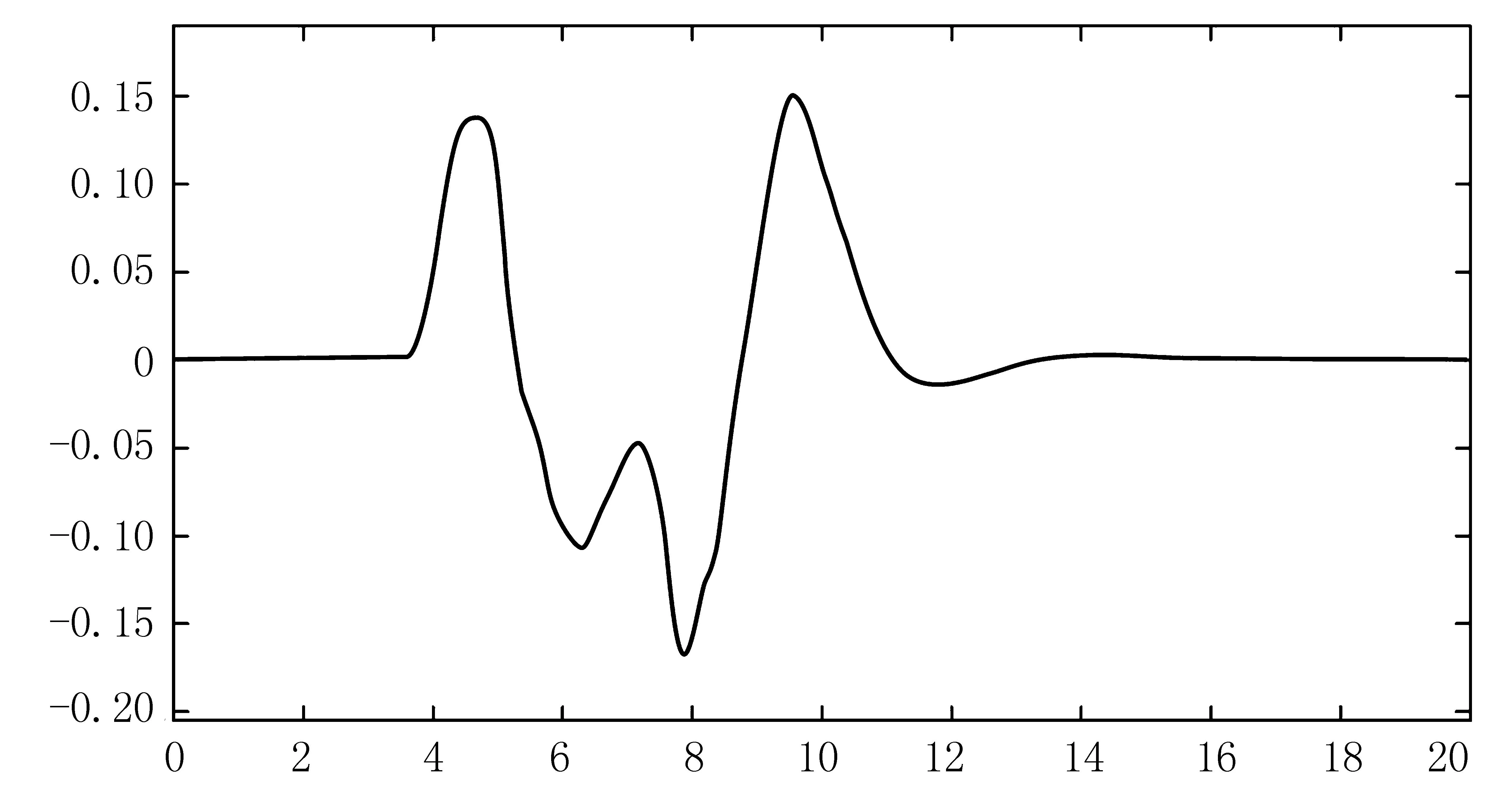
图8 质心侧偏角Fig.8 Sideslip Angle of centroid

3.2 基于滑模变结构路径跟踪控制算法的联合仿真分析

3.2.1 Simulink模型的建立

首先,建立滑模变结构控制算法控制误差的Simulink模型,即理想的横摆角速度与实际横摆角速度之差,如图9所示。

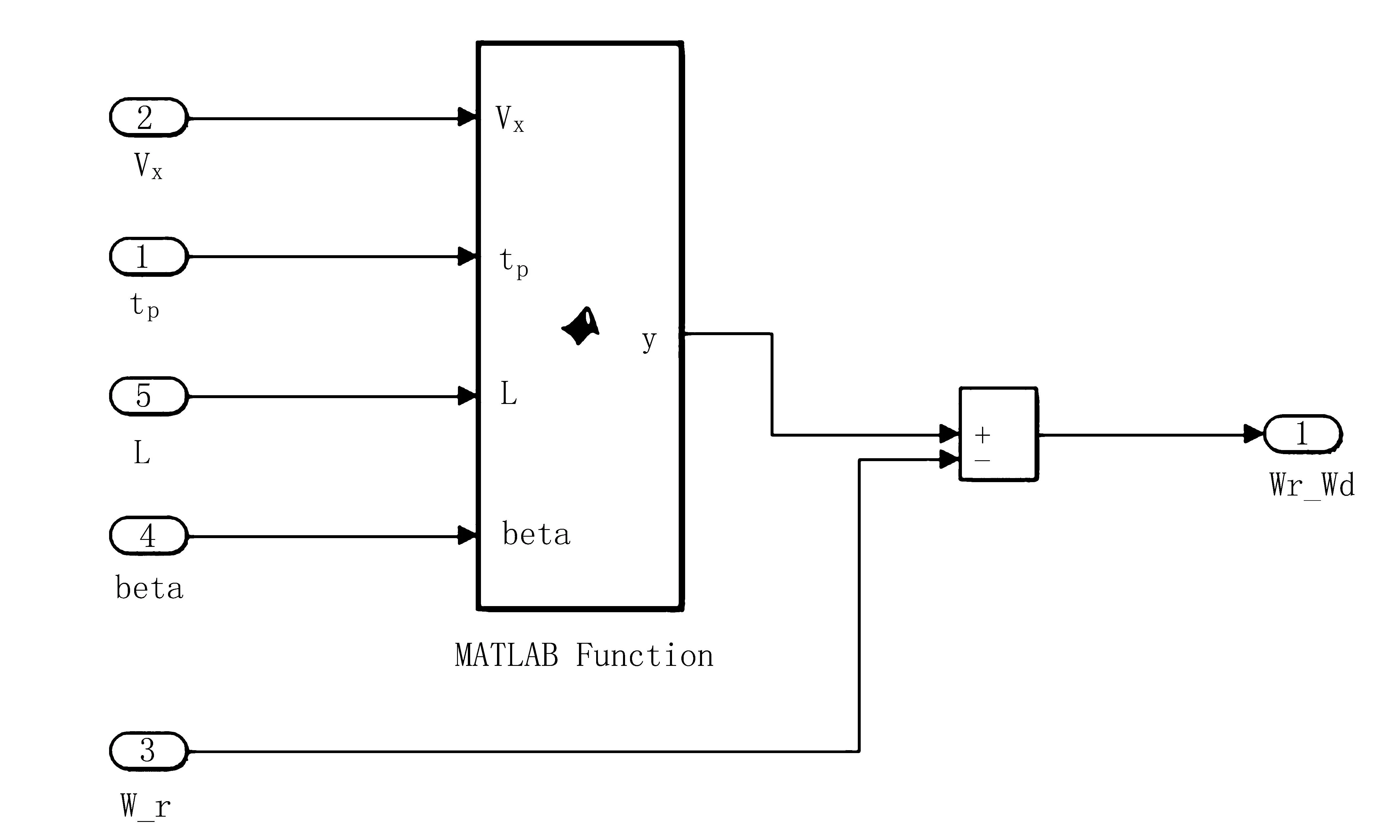
图9 滑模变结构控制误差的Simulink模型Fig.9 Simulink model of sliding mode variable structure control error

图9中,Vx为纵向车速,tp取0.6s,L为预瞄点的预瞄距离,beta为质心侧偏角,w_r为实际的横摆角速度,y为理想的横摆角速度。

根据滑模变结构控制算法的切换函数及控制规则,建立Simulink模型,如图10所示。

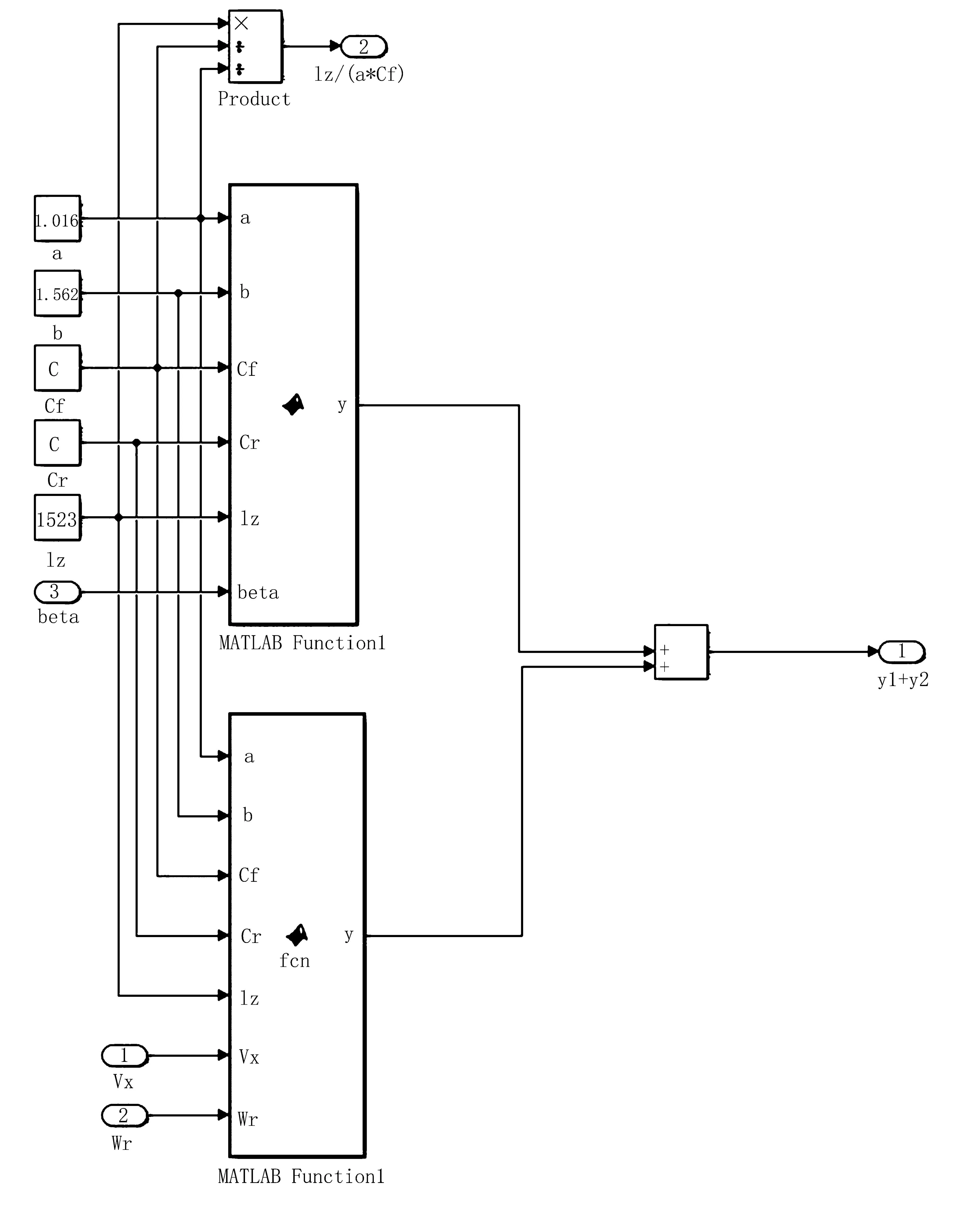
图10 滑模变结构控制的切换函数及控制规则的Simulink模型Fig.10 Simulink model of switching function and control rule of sliding mode variable structure control

根据滑模变结构控制的控制规律建立Simulink模型,如图11所示。

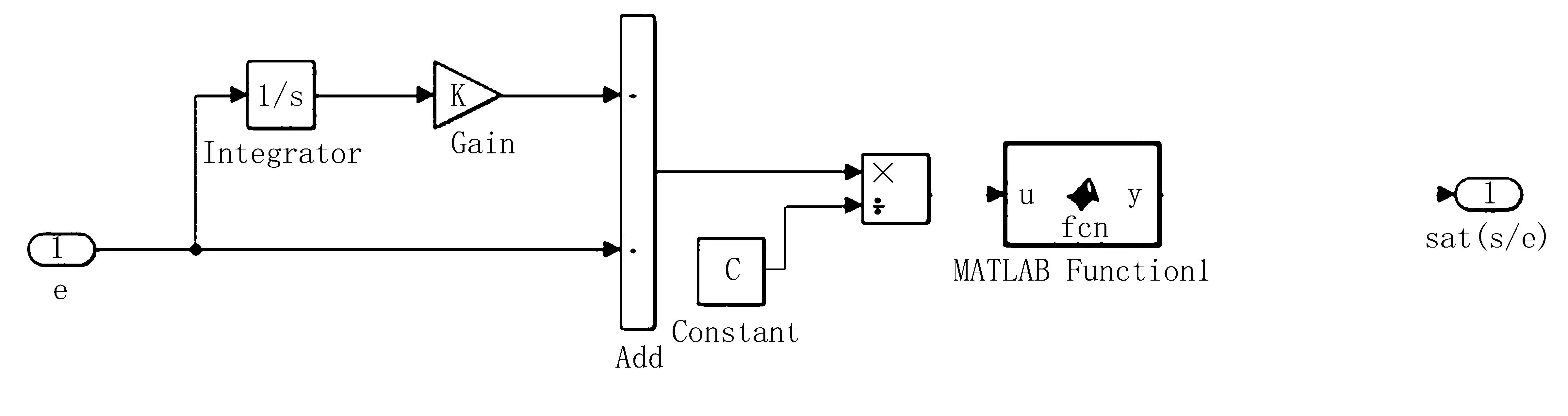
图11 滑模变结构控制规律的Simulink模型Fig.11 Simulink model of sliding mode variable structure control law

建立汽车的左(右)前轮转矩的Simulink模型,如图12所示。

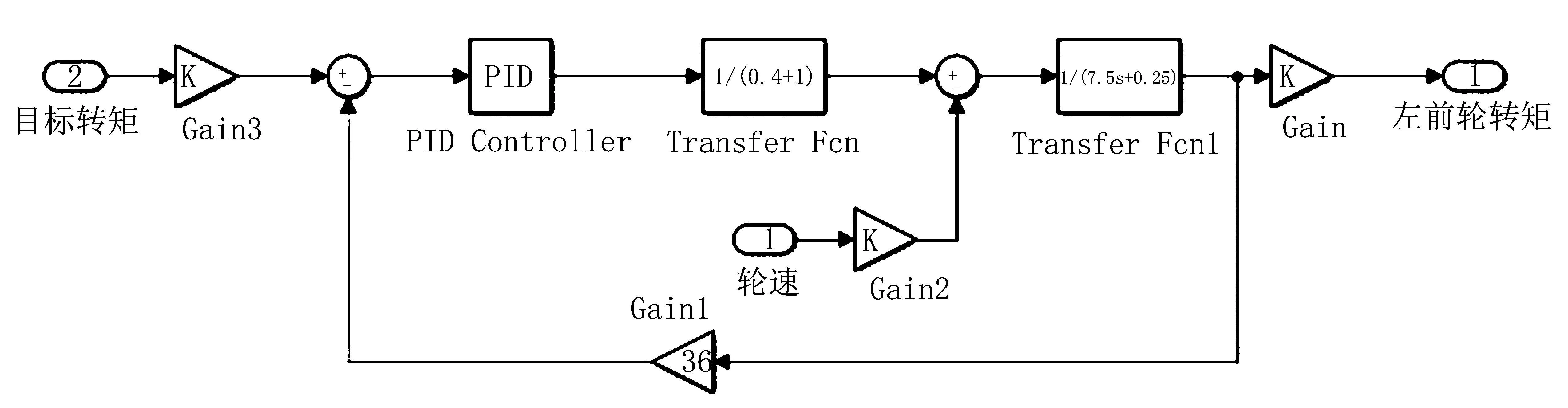
图12 整车左(右)前轮转矩的Simulink模型Fig.12 Simulink model of vehicle left (right) front wheel torque

3.2.2 CarSim模型的建立

整车参数的选择与PID算法相同,道路图形如图13所示。

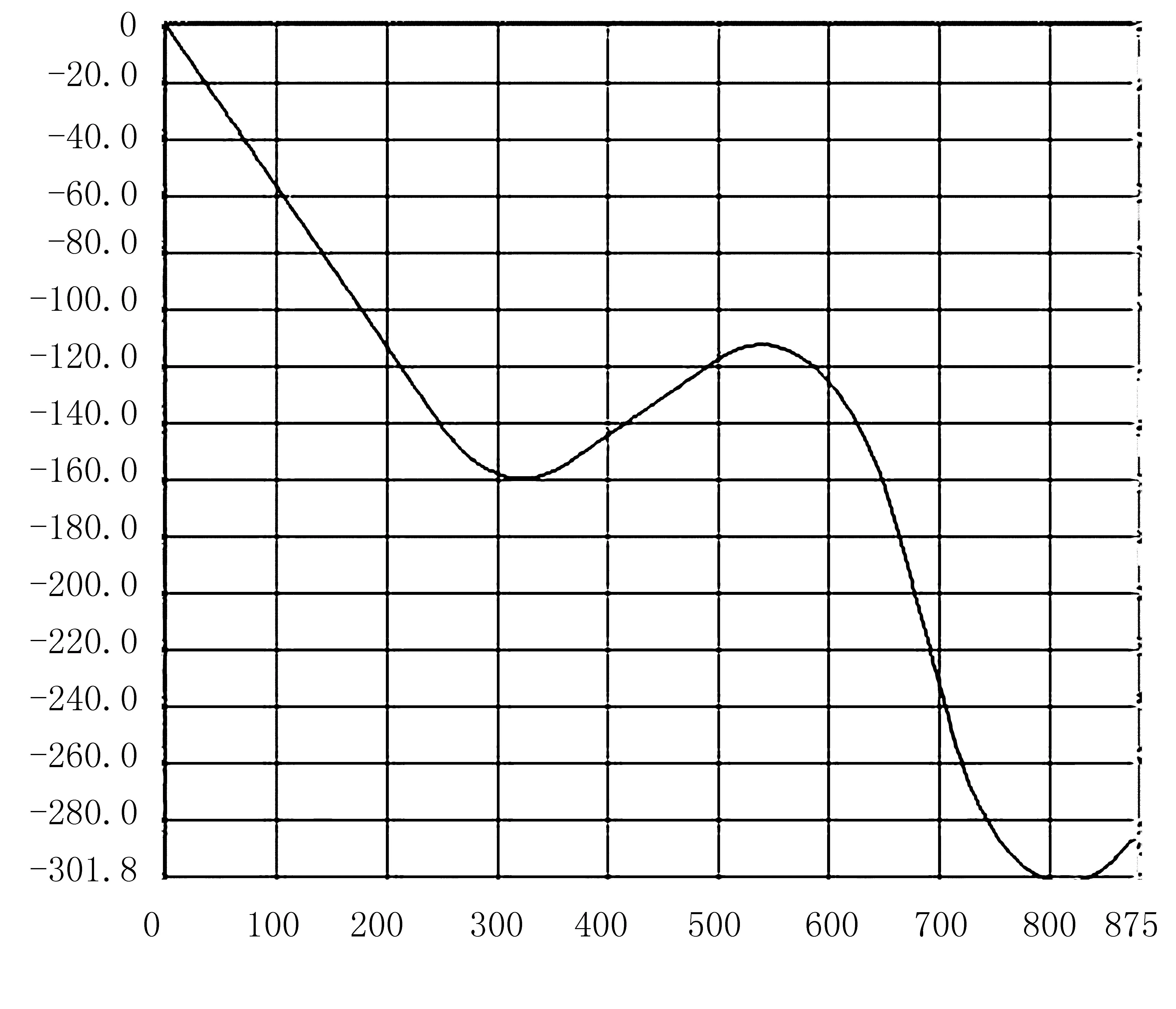
图13 滑模变结构控制算法的CarSim道路图形Fig.13 CarSim road graph of sliding mode variable structure control algorithm

方向盘转角、左前轮转矩、右前轮转矩为CarSim整车模型的输入,纵向车速、横摆角速度、质心侧偏角、预瞄点的预瞄距离、理想的X坐标、理想的Y坐标、实际的X坐标、实际的Y坐标、轮速、横向偏差为CarSim整车模型的输出。

进行联合仿真分析,结果如图14～16所示。联合仿真后,得到了两种算法的实际路径与参考路径对比图。根据曲线可知:基于预瞄时间自适应的 PID路径跟踪控制算法的图像在汽车拐弯时超调量较大,跟踪效果不理想;基于滑模变结构路径跟踪控制算法的路径图误差较小,两条曲线接近于重合状态,跟踪效果较好,车辆转弯时横向偏差控制在0.45m之内。因此,滑模变结构路径跟踪控制算法相对于PID路径跟踪算法的路径跟踪精度更高,对路况的适应性更好,更适用于无人驾驶农机车辆的路径跟踪控制。

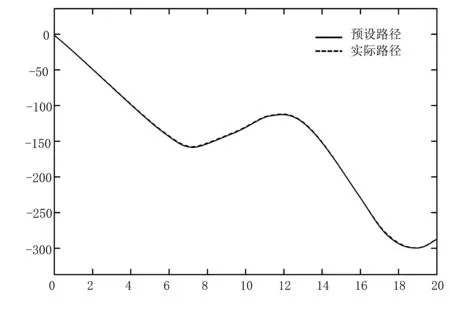
图14 实际路径与参考路径对比图Fig.14 Comparison between actual path and reference path

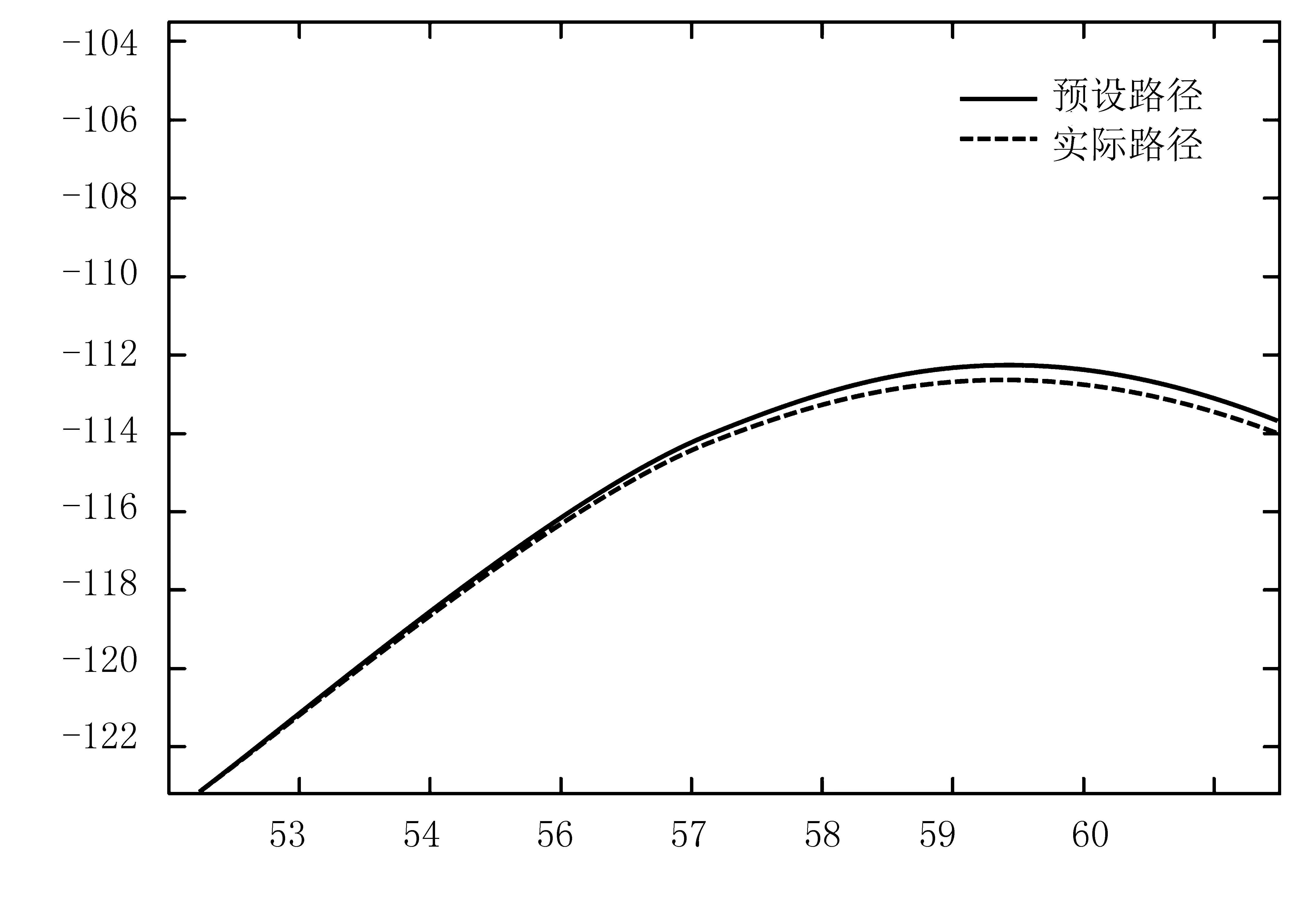
图15 实际路径与参考路径对比局部放大图Fig.15 local enlargement of comparison between actual path and reference path

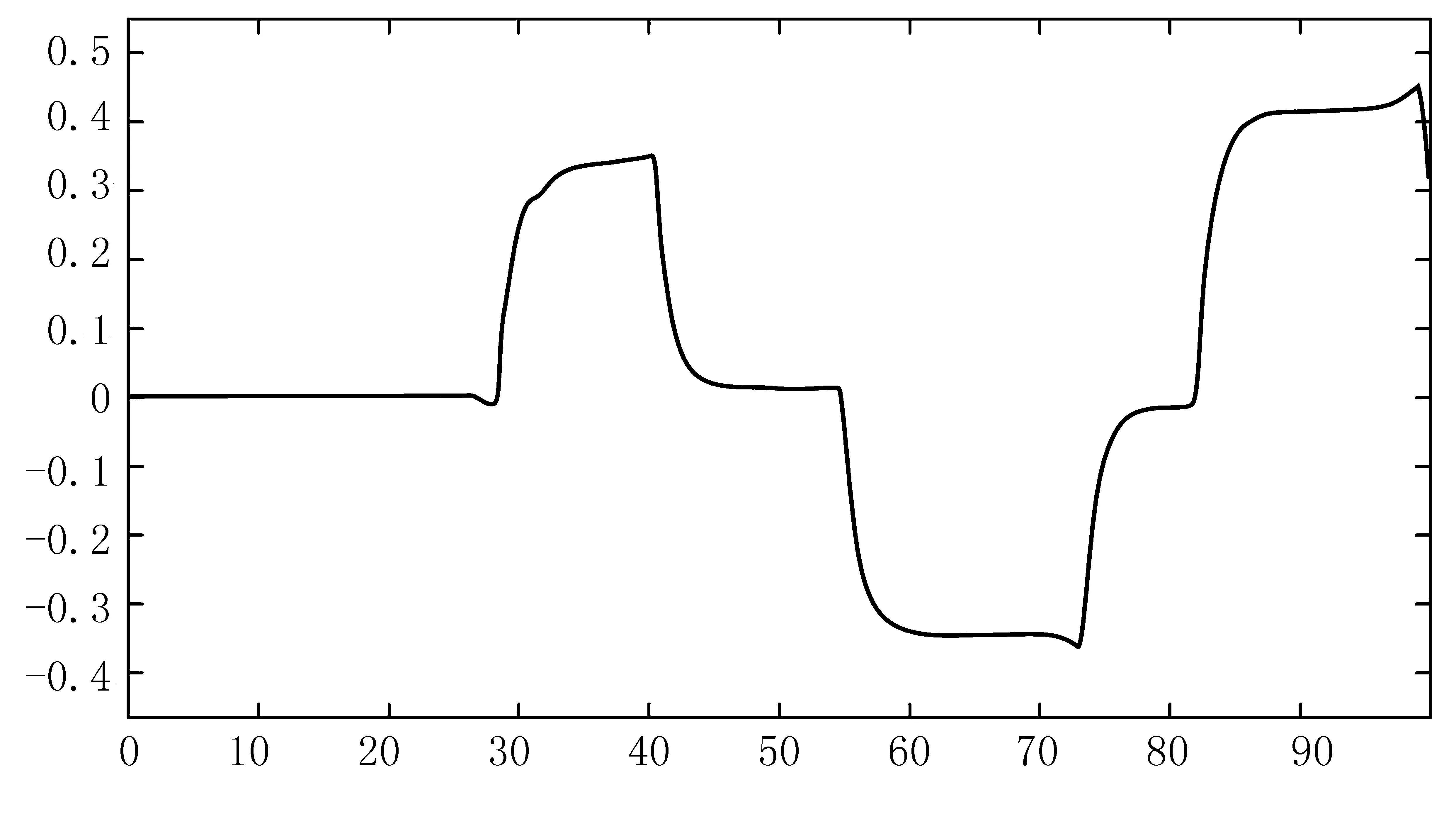
图16 横向偏差图Fig.16 Transverse deviation diagram

4 结论

1)根据车辆运动学模型与线性化二自由度模型,通过增加控制量极限约束,求解了结构控制器控制规律,建立了基于滑模变结构控制算法路径跟踪控制器,使得车辆实际转角与理想转角误差最小化,保证对路径跟踪的平稳性。

2)利用Simulink与CarSim建立联合仿真,对加入预瞄时间自适应模块的PID控制算法及滑模变结构路径跟踪控制算法进行仿真。结果表明:较加入预瞄时间自适应模块的PID控制算法,滑模变结构跟踪效果比较理想,实际路径与期望路径的误差较小,横向偏差控制在0.45m内,具有响应快、抗干扰能力强、操作简单等优点,是一种适用于农机的路径跟踪算法。