库岸滑坡涌浪链生灾害动力学研究进展*
2024-01-11徐文杰
徐文杰
(清华大学,清华大学水圈科学与水利工程全国重点实验室,北京 100084,中国)
0 引 言
滑坡涌浪是近水滑坡灾害链上的一个重要致灾方式,一直以来是国内外工程地质、水利工程领域等研究的难点和热点。尤其,随着大规模水电工程建设的不断开展,库区滑坡及涌浪灾害问题将直接影响水域航道、库区沿岸居民及工程安全,甚至大坝和电站安全运营。
滑坡涌浪灾害在国内外时有发生。1958年美国Lituya海湾发生的大型滑坡(3060×104m3,岩质)(图1),涌浪在对岸爬升达524m,波速达到150~200km·h-1(Fritz et al.,2009); 1959年意大利的庞特塞拱坝库区发生滑坡(300×104m3,岩质)形成20m高的涌浪,使坝体漫顶; 1963年意大利瓦伊昂水库左岸滑坡(近3×109m3,岩质)形成250m高的涌浪,震惊整个工程技术界(钟立勋,1993); 2017年6月格陵兰岛海岸的Nuugaatsiaq村发生大型滑坡(5800×104m3,岩质),形成100余米高的涌浪(Quirin,2017)。
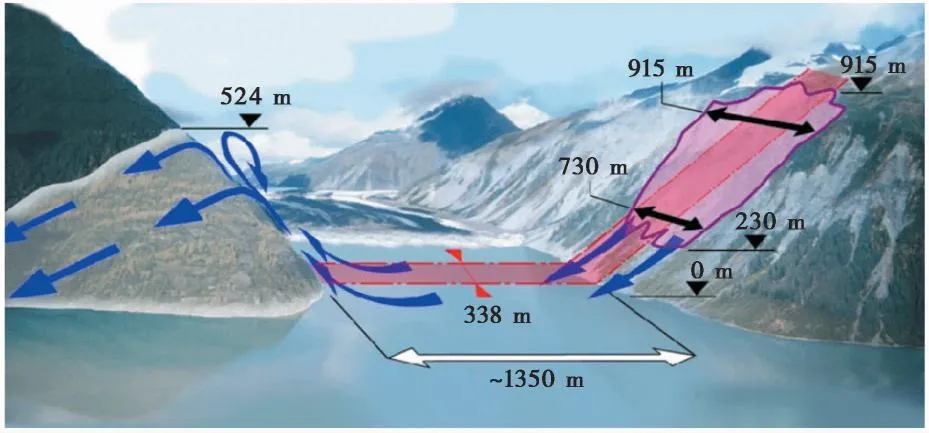
图1 1958年美国Lituya海湾的滑坡涌浪(Fritz et al.,2009)
我国随着水电工程建设的飞速发展,因库区滑坡涌浪而带来的灾害损失更是屡见不鲜。1961年2月柘溪水库蓄水期间,近坝库区右岸发生滑坡(165×104m3)形成21m高的涌浪,3.6m高的涌浪翻过正在施工的坝体(杜伯辉,2006); 2007年6月水布垭库区的大堰塘滑坡(300×104m3)涌浪在对岸爬坡高达50m 左右,下游20.8km 大坝处涌浪爬坡仍高4m左右(殷坤龙等,2008)。2009年7月小湾电站库区坝上游的荒田滑坡(300×104m3),造成30余米高的涌浪(吴佳壕,2011)。此外,据统计1982~2001年期间三峡库区发生地质灾害70余次,其中规模较大的有40余次(国土资源部,2001),如:1982年7月的鸡扒子滑坡(1500×104m3),将滑坡前缘长江岸坡向江中推进50余米,并形成巨大涌浪(李玉生,1984); 1985年6月的新滩滑坡(3000×104m3),形成涌浪在对岸最大爬坡高度达近50m(骆培云,1988); 2003年的千将坪滑坡(2400×104m3),形成近30m高的涌浪(王治华等,2003); 2008年龚家方滑坡(38×104m3),形成涌浪在对岸最大爬坡达13余米,影响范围超过10km(Huang et al.,2012); 2015年6月巫山县大宁河江东寺北岸发生滑坡(2.4×104m3)涌入库区形成6m高涌浪(Huang et al.,2016)。
库岸边坡的失稳及涌浪是一个涉及滑坡动力学、岩土力学及流体力学等多学科的链生灾害动力学问题,也是一个复杂的“流-固”耦合问题(图2):一方面,库水位波动、降雨等水力条件是影响库区滑坡稳定性及灾变的重要因素; 另一方面,形成涌浪的过程实质上是高速运动的滑坡体(固体)与水体(流体)相互作用的复杂过程; 其次,涌浪在传播过程中遇到岸坡、船舶及大坝等工程结构时产生的冲击、爬坡等灾害效应也是“流体”与“固体”的相互耦合过程。随着一些灾难性滑坡涌浪事故的发生,库岸滑坡涌浪问题的研究逐渐被国内外众多学者所关注,并纷纷从不同角度开展了相关研究工作。
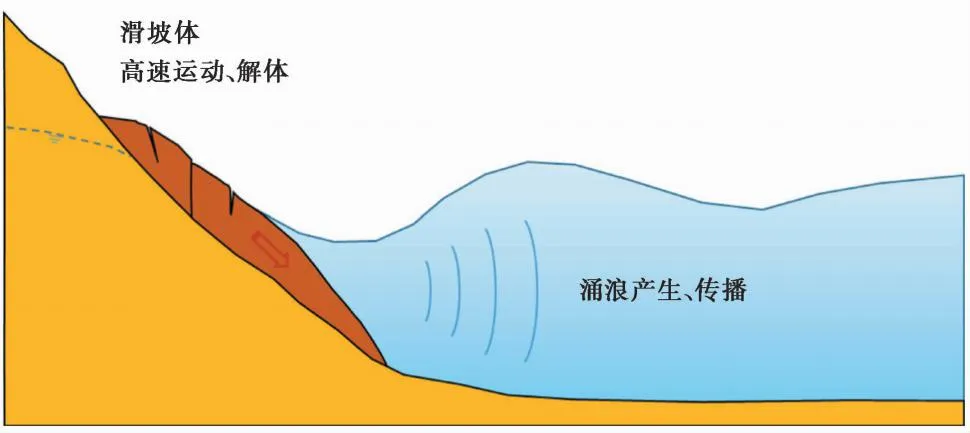
图2 滑坡涌浪过程示意图
为了进一步推动滑坡涌浪灾害的分析方法的发展,本文系统地归纳总结了国内外现有库岸边坡稳定研究现状,以及滑坡涌浪分析的3大类方法,即:物理模型试验法、解析法及数值模拟法。并对现有研究的成果和不足进行了分析,在此基础上探讨了滑坡涌浪分析的关键问题及前沿方法,提出了基于FEM-SPH-DEM耦合的库岸滑坡涌浪分析方法。
1 水动力环境下库岸边坡稳定分析
库岸边坡的失稳破坏是诱发涌浪的触发因素。降雨、库水位变动等水动力环境是诱发库岸边坡失稳的一个的重要外部因素(中村浩之等,1990; 薛果夫,等1998; Fiorillo et al.,2004; Mikos et al.,2004; 闵弘等,2004; Chang et al.,2005; Crosta et al.,2006)。
在降雨诱发土石混合体滑坡灾方面,国内外众多学者在该领域开展了大量的研究工作。胡明鉴等人(2002),通过大型野外人工降雨试验模拟研究了土石混合体斜坡暴雨、滑坡及泥石流的共生关系。俞伯汀等(2006)采用室内物理模型试验研究了土石混合体边坡内存在的地下水管道排泄系统形成过程及对斜坡稳定的影响。周中(2006)采用室内及现场试验方法也研究了土石混合体的渗透破坏特性。Sassa(1998)在对日本发生的泥石流研究的基础上,提出滑体的运动使得滑面处颗粒的破碎,从而导致滑面处土体液化,进而造成滑体的高速、远程滑动现象。Wang et al.(2003)通过室内环剪试验揭示了滑坡触发泥石流演变模式及形成机理,指出了孔隙水压力的产生是滑坡突变失稳的动因。Chae et al.(2012)指出降雨引起的滑坡体的体积含水率变化比孔隙水压力波动更加明显,提出将边坡的体积含水率梯度作为滑坡预测的失稳阀值。汪丁建等(2016)基于Green-Ampt(GA)模型,同时考虑湿润锋以饱和带渗流作用,推导了一种新的滑坡降雨入渗函数,弥补了GA 模型只适用于无限长坡的不足。
在库水位变动作用下滑坡灾害研究方面,王士天等(1997)通过大量的实际资料研究指出水库滑坡有两种:一种是库水位达到敏感水位后滑体内孔隙水压力分布达到新的平衡过程中产生的滑坡; 一种是发生在库水位消落时的滑坡。Luciano(2007)研究表明水库蓄水引起的孔隙水压力变化控制着边坡位移与力学变化行为。贺可强等(2017)针对库水涨落诱发滑坡致灾机理,提出了以库水位下降引起的边坡下滑动力增量作为边坡的加载动力参数。胡修文等(2005)、Timpong et al.(2007)、贾官伟等(2009)、赵代鹏等(2013)、黄佩伦等(2020)、肖捷夫等(2020)分别采用模型试验的方法,分析了库水位变动作用下坡体内地下水位和有效应力变化情况,在此基础上对滑坡失稳机理进行了探讨。柴军瑞等(2004)、郑颖人等(2004)、刘新喜等(2005)及汪斌等(2007)分别采用有限元数值计算的方法系统研究了库水位变动环境下坡体内地下水位变化及对边坡稳定的影响。
水库蓄水后库岸岩土体的水-岩相互作用是一个复杂的物理-力学-化学耦合过程,将导致其物理力学状态的劣化。尤其水库长期运行过程中,消落带范围内的岩土体,一方面受强烈水动力作用的影响,导致内部细小矿物颗粒不断带走、掏空; 另一方面,岩体在强烈干-湿循环作用下,强度不断降低。这两种作用相互促进,加速岩土体的劣化发展。徐文杰等(2006)通过对天然及浸水后土石混合体的野外试验研究表明,浸水后由于细粒被带走导致黏聚力降低而摩擦角略有提升。此外,对水-岩作用下砂岩(刘新荣等,2008; 邓华锋等,2015)、千枚岩(崔凯等,2019)及红层软岩(谢小帅等,2019)等劣化规律进行了实验研究。殷跃平等(2021)通过调查研究发现三峡库区水位消落带岩体劣化松动使得部分岸坡加速朝不稳定方向演化,给溶蚀岩体岸坡带来了工程灾变效应问题; 并通过对三峡库区的灰岩浸泡-风干循环后力学参数研究表明,平均每循环下降率约为0.7%,随着循环次数的增加岩样强度下降可用指数函数形式拟合(黄波林等,2019)。
徐文杰等(2009)基于有限元及强度折减法对库水位骤降过程中的流-固耦合及相应的稳定性变化特征进行了系统研究,表明库水位作用下库岸边坡的稳定性演化是水动力环境与边坡岩土体强度相互博弈的过程:库水位骤降对边坡稳定性影响较大,且其稳定系数下降随着骤降幅度的增大而增大; 而库水位上升过程中,边坡的稳定性有所下降,当上升至某一临界水位后边坡稳定系数达到最低值,而后随着库水位的上升其稳定系数有所回弹(图3)。当然这种演化规律还取决于具体的边坡工程地质结构特征及与库水位的空间关系。
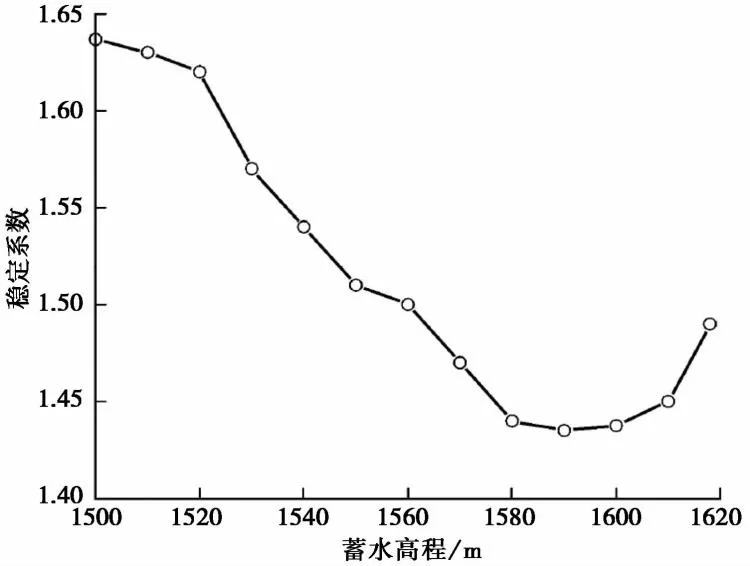
图3 边坡稳定系数随蓄水高程的变化曲线(徐文杰等,2009)
在近几年来,随着我国大型水电工程的建设越来越多的学者开始关注降雨与库水位共同作用下滑坡灾害问题。李晓等(2004)针对降雨和库水位变动联合作用下滑坡地下水动力场计算问题,提出了一种考虑降雨与库水位逐日变化的库岸地下非稳定渗流场的计算模式。罗先启等(2005)、李卓等(2017)开展了降雨及库水位共同作用下滑坡大型模型试验研究,系统分析了降雨及库水位共同作用库岸滑坡的灾害机理。在数值计算分析方面,刘新喜(2003)采用自编计算机程序开展了库水位骤降与降雨耦合作用下滑坡体稳定性计算; 连志鹏等(2011)、郑慧等(2012)、周永强等(2014)、王力(2014)及方四发(2016)等基于饱和-非饱和渗流理论分析了在降雨和库水位变化的同时作用下,滑坡体内地下水渗流场及斜坡稳定系数的变化; 朱鹏谱(2008)、张桂荣等(2011)基于极限平衡法,对不同降雨强度及库水位变动条件下的滑坡进行了稳定性分析,以研究最不利滑坡稳定的工况。
2 滑坡涌浪模型试验研究
物理模型试验是滑坡涌浪研究的重要手段,以揭示滑坡涌浪灾害机理与规律,同时在此基础上提出相应的解析计算公式。Wiegel et al.(1970)利用水动力模型试验研究了滑坡涌浪与滑块宽度、弗劳德数、水深及滑体速度等之间的关系。Kamphis et al.(1971)通过试验的方法指出涌浪高度主要取决于滑体的体积及滑体的弗劳德数,并建立了相关关系。Enet et al.(2003),Fritz et al.(2003)、Altaie-Ashtiani et al.(2008)、Marcello et al.(2009)及Heller et al.(2015,2016)也分别采用不同形式的室内模型试验研究了影响滑坡涌浪高度的因素、涌浪传播特征及机制等; 尤其Ataie-Ashtiani et al.(2008)通过120组模型试验分别从坡角、水深、入水速度、滑体几何形状(8种)、滑体密度及变形特性等影响因素着手开展研究,提出了涌浪波幅与周期的经验公式。Heller et al.(2015)基于滑坡涌浪三维模型试验研究了水体几何特性对近场及远场涌浪的影响,并提出了相应的经验公式,同时基于SPH数值计算揭示了滑坡滑动及涌浪的动力学特性(Heller et al.,2016)。为研究松散滑坡涌浪特性,Ball(1970)、Davidson(1975)等率先开展了相关研究工作; Heller et al.(2011)通过200多组矩形水槽模型试验,研究了静水深度、冲击速度、冲击角度、滑坡厚度、体积、密度及粒度组成等对涌浪的影响,建立了滑坡涌浪波幅及周期与冲击波参数的半经验关系。Huber et al.(1997)开展了1000组2D和3D的散体颗粒涌浪模型试验,指出涌浪波高主要取决于滑体体积与宽度之比。Fritz et al.(2004)和Mohammed(2010)开展了松散滑坡的2D和3D涌浪大型模型试验,并将粒子图像测速(PIV)技术、多重声学传感测量技术、激光测距仪、波高仪、高速摄像机等应用于试验全过程量测,系统研究了滑坡体体积形状、冲击速度等对涌浪的影响,并根据试验结果提出了首波波幅的衰减及波长和周期方程。Mulligan et al.(2017)在二维模型试验的基础上研究了散体滑坡入水过程中滑坡体与水体间的动量传递,并提出了相应的用于预测近场涌浪波幅的半经验公式。Francesco et al.(2017,2021)研发了用于模拟高速散体滑坡涌浪的室内模型试验装置(图4),并首次采用计算机视觉、PIV等技术实现涌浪的三维量测,通过40多个模型试验提出了滑坡体参数与涌浪首波波幅、传播特征及能量的关系; 通过对滑坡涌浪过程中能力转换分析表明,52%消耗于滑坡体与滑动面的摩擦,42%消耗于湍流等过程,而只有6%传递给形成的涌浪(Francesco et al.,2021)。
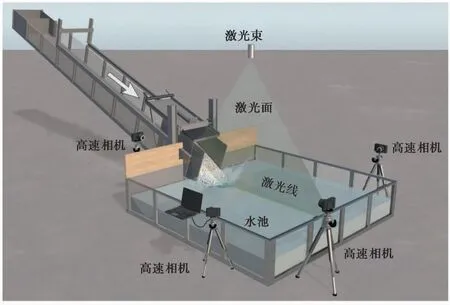
图4 Francesco et al.(2021)采用的滑坡涌浪模型试验装置图
伴随着大型水电工程建设,我国学者也开展了系列滑坡涌浪模型试验研究。如,殷坤龙等(2012)采用室内大型模型实验,研究了滑坡规模、入水速度、滑动面倾角、水深、岸坡坡角等因素对涌浪高度的影响; Wang et al.(2017),Huang et al.(2020)通过室内模型试验对滑坡涌浪形成机制和传播衰减效应开展了系统的研究; 韩林峰等(2018)基于浅水区和深水区的滑坡涌浪模型实验,基于动量守恒原理,提出了最大近场拨付的预测模型。此外,针对水电工程库区遇到的一些滑坡,也开展了针对具体库区滑坡的涌浪模型试验研究(如,小浪底水利枢纽(叶耀琪,1982)、李家峡电站(陶孝铨,1994)、三峡库区(黄波林等,2013; 何庆,2014)、古水电站(丁军浩等,2017)等),以研究库区滑坡可能产生的涌浪灾害。
3 基于解析法的滑坡涌浪研究
在滑坡涌浪早期的预测分析中主要为解析法。Kennard(1949)从流体力学的连续方程和运动方程出发提出了运动物体产生的表面波的解析工程,Noda(1970)在此基础上考虑了滑坡体垂直下落和水平推动两种极端情况,给出了运动物体引起涌浪高度与水深及运动速度的简单关系式; 后续许多学者又基于Noda法进行了改进和发展,包括我国的潘家铮(1980)和陈学德(1984)等。Slingerland et al.(1979)、Frite et al.(2003)对滑坡涌浪及传播函数等进行了探讨。此外,基于实际工程案例及模型试验成果,许多学者也提出了相应的经验公式法,如:Ataie-Ashtiani et al.(2007)通过大量滑坡涌浪模型实验数据,提出了大型滑坡涌浪波高的经验关系; Wiegel et al.(1970)基于模型试验提出了滑坡涌浪与滑体宽度、水深、Froude数及滑体速度等因素的关系; Valentin(2009)在总结部分经验公式的基础上,提出了不同类型滑坡涌浪的最大浪高、传播浪浪高及爬高等的计算公式。黄种为等(1983)根据3个工程的模型试验,初步探讨了滑坡涌浪的计算方法,并指出滑速和滑体体积是影响滑坡涌浪高度的主要因素,并提出了较为简单的估算方法; 汪洋等(2004)从明渠非恒定流出发,提出了滑坡失事点涌浪的衰减变化规律,并据此进行涌浪高度的叠加以得到滑坡失事点最终涌浪高度的方法。黄波林(2014)将水波动力学模型应用于滑坡涌浪灾害模拟,并将其应用于三峡库区龚家方滑坡涌浪灾害模拟取得了较好的效果。
4 滑坡涌浪数值模拟方法
随着数值计算技术的发展,在滑坡涌浪模拟方面取得了飞速的发展,尤其近几年来许多学者开展了相关研究,大致可以分为基于单一流体动力学和基于流-固耦合的方法两大类。
4.1 基于单一流体动力学的滑坡涌浪数值分析
基于单一流体力学计算方法,将滑体视为刚形体或非牛顿流体,从而大大简化了滑坡涌浪数值分析方法。这方面的主要有:Davidson et al.(1975)及 Raney et al.(1976)利用有限差分法和实验模拟计算对滑坡涌浪问题进行了研究,得出滑体最大速度与涌浪高度的关系; Pastor et al.(2009)采用欧拉算法将滑体和水分别视为两种流体,对滑坡的涌浪问题进行了分析;Serrano-Pacheco et al.(2009),Basu et al.(2009),Abadie et al.(2010),Bosa et al.(2011)采用有限体积的方法对滑坡涌浪问题进行了模拟,Basu et al.(2009)和Bosa et al.(2011)分别将其应用于Lituya滑坡及瓦伊昂库区滑坡涌浪灾害; Cremonesi et al.(2011)采用拉格朗日有限元方法对滑坡涌浪问题进行了模拟;Zhao et al.(2016,2017)将滑坡体简化为非牛顿流,基于有限元法提出了一种改进的水平集守恒法用于三维滑坡涌浪与传播过程的三相流模拟(滑坡体、水与空气)。Xiao et al.(2015)提出了一种用于模拟流体和类流体运动的Tsunami Squares方法,将其应用于三峡库区龚家方滑坡运动、涌浪及传播全过程的模拟。
近几年来,光滑粒子流体动力法(SPH)在流体分析领域有了广泛的应用和发展。Altaie-Ashtiani et al.(2008a,2008b)、Shi et al.(2016)、Shahab et al.(2017)将数值试验与物理模型试验进行了对比验证取得了较好的效果,Vacondio et al.(2013)将其应用于瓦伊昂滑坡涌浪产生、传播及冲击坝体溃坝过程研究(图5)。
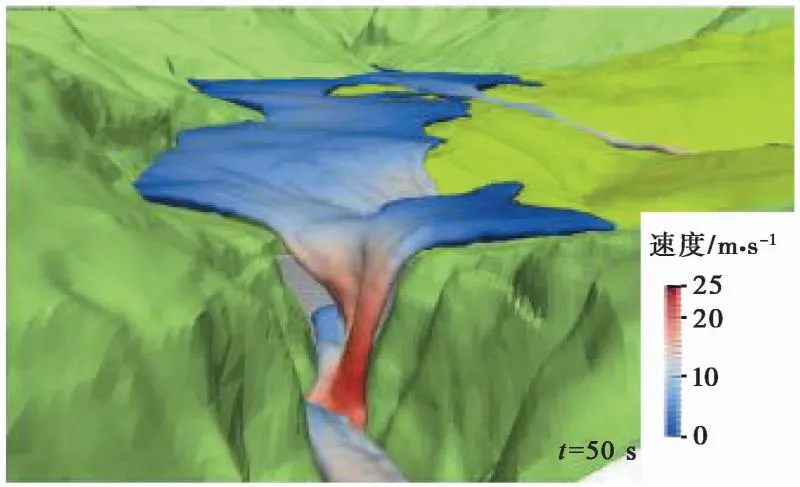
图5 Vacondio et al.(2013)基于SPH方法得到的Vajont滑坡涌浪速度(50s)
4.2 基于流-固耦合的滑坡涌浪数值分析
滑坡涌浪是一个复杂的流-固耦合过程。为了更好地描述滑坡体(固体)与水体(流体)间的相互作用,充分利用不同的计算方法各自的优势,基于固体力学与流体力学耦合的计算分析方法成为一个新的研究方向。徐文杰在(2012)探讨了耦合的欧拉与拉格朗日算法(CEL)在滑坡涌浪研究应用中的可行性。离散元法(DEM)、大变形不连续分析(DDA)在滑坡动力学模拟中有强大的优势,并取得了很好成果。Mikola et al.(2014)、Wang et al.(2016)采用DDA及Tan et al.(2017)采用DEM来模拟滑坡体,并与SPH(模拟水体)进行耦合,模拟滑体入水涌浪,并与物理实验进行了对比验证,取得了较好的效果。此外,Zhao T et al.(2016)采用CFD-DEM耦合的方法分析了Vajont 滑坡涌浪过程。
Xu et al.(2021)研发了基于GPU加速并行的SPH-DEM耦合模拟程序CoSim-SPHDEM(图6),并通过与Fahad(2010)的模型实验对比,系统地验证了SPH-DEM耦合法在滑坡涌浪分析中的可行性,并对体积相同的散体滑坡(Sg)、矩形块体(Sc)、前缘为45°的楔形体(Sw)、两个块体(St)及4个块体(Sf)等5种模型开展了数值实验分析,研究了滑坡体的形态、类型等对滑坡涌浪过程中的能量转化机制及涌浪特征的影响(图7)。研究表明:滑坡体产生的涌浪首波传播速度为Sf>St>Sc>Sw>Sg; 形成的涌浪首波波幅,为Sf>St>Sc≈Sw>Sg。
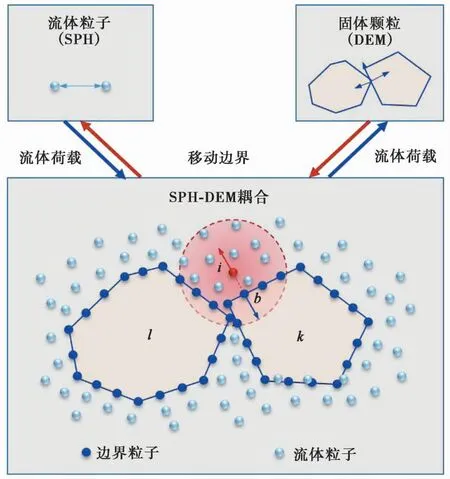
图6 CoSim中SPH-DEM耦合图示
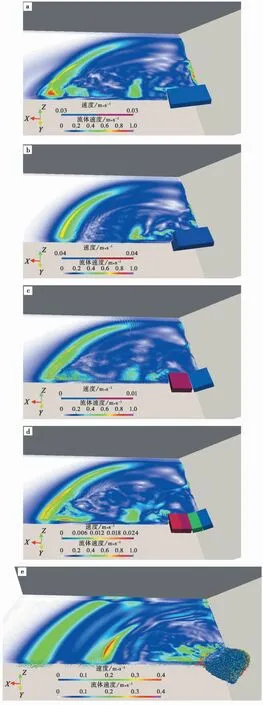
图7 相同体积不同类型滑坡涌浪分析(Xu et al.,2021)
5 基于FEM-DEM-SPH耦合的滑坡涌浪分析
纵观目前对滑坡涌浪的分析方法可以看出,数值计算尤其是基于流体-固体耦合的数值计算方法(如,SPH-DEM,CFD-DEM等)可以较好的模拟滑坡体的变形破裂过程、又可以实现滑坡体与水体的强烈的非线性耦合作用,进而实现涌浪的流体动力学模拟,从而为滑坡涌浪分析提供了强有力的支撑。与基于有限体积(FVM)的流体动力学(CFD)数值计算方法相比,基于粒子的SPH数值方法可以较好地实现滑坡冲击水体及涌浪过程中的“碎波”。
滑坡的范围、变形及破坏过程等特征是涌浪形成的诱发因素。因此,滑坡这些特征的精细化模拟与分析是滑坡涌浪分析的关键。DEM虽然在模拟滑坡灾害动力方面有较好的优势,但是由于其细观参数选取方面存在一定的瓶颈,在实现滑坡体稳定性定量分析时依然有不同的观点。而相交于DEM而言,基于FEM的强度折减法则在滑坡稳定性定量评价及滑动面预测等方面有了很好的应用。
因此,构建多种方法的耦合(联合)分析(图8),充分利用不同分析方法的优势,实现滑坡涌浪的不同阶段、不同过程的分析,是建立合理的滑坡涌浪分析和评价方法的关键。针对具体的滑坡体,基于FEM法开展降雨及库水位变动等水动力环境下库岸边坡稳定性的演化过程、失稳范围及失稳机制的定量分析和评价; 在此基础上,基于DEM实现构成滑坡体的颗粒接触参数的反演与分析,从而实现灾害动力学过程的模拟与预测; 最终,基于SPH-DEM方法实现滑坡涌浪、涌浪传播等链生灾害动力学全过程的模拟与分析。
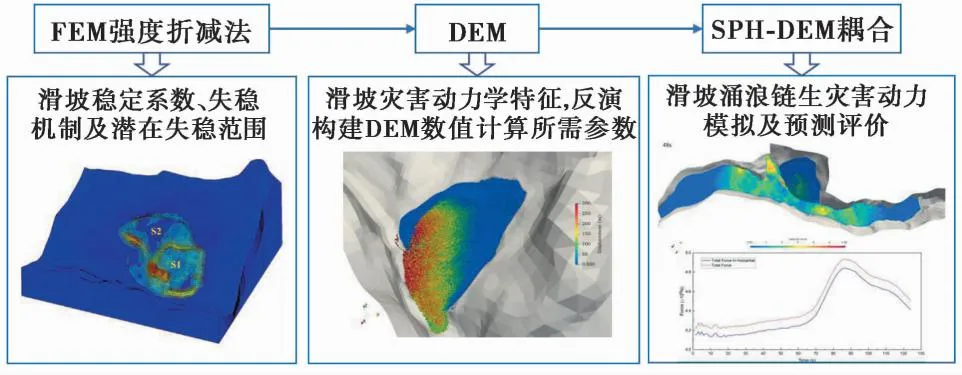
图8 FEM-SPH-DEM滑坡涌浪链生灾害动力学分析思路
6 结 论
随着世界各国水电工程建设的不断发展,尤其是梯级水电工程群的建设,滑坡涌浪链生灾害动力学过程是影响甚至至于水电工程(群)稳定性的重要因素。建立合理的分析与评价方法,将对于优化工程建设、防灾减灾具有重要的理论意义和工程价值。
水动力环境的剧烈变化是影响库岸边坡稳定性的重要外部诱发因素。因此,构建水-岩耦合的数值分析方法,是目前库岸滑坡稳定性演化及评价的发展趋势。
在滑坡涌浪灾害方面的研究:解析法通常将滑坡体视为一个刚性体或刚性条块集合,通过研究刚体质心的运动,将其视为移动的边界,极大地忽略了滑体与水体间的强耦合作用; 物理模型试验的方法固然能够在解决滑坡涌浪问题方面具有一定的优势,但是由于其试验费用较高,而且模型的缩尺效应在一定程度上也会影响试验的结果; 数值计算方法为深入研究滑坡涌浪问题开辟了新的方法,尤其是近些年来随着计算机技术及数值算法的不断发展,在滑坡涌浪灾害分析方面体现了强大的优势,当然由于涉及岩土体-水耦合、多相流及流体自由面等复杂的数值计算问题也给数值计算带来了新的挑战!
滑坡体的运动状态对其涌浪起决定性作用,滑坡变形破坏机理是研究其运动状态的重要基础。滑坡体的渐进破坏和启动取决于自身的地质条件及外动力诱发因素; 运动过程滑坡将不断破裂、解体,这种结构的改变进而又影响着外动力对其运动状态的影响。滑坡的灾害过程也是滑坡与外动力(如,降雨、地下水、地表水等)的强耦合过程。传统的滑坡涌浪灾害研究中,将滑坡体视为刚性体或非牛顿流体,忽略了滑坡灾害机理,甚至忽略了滑坡体与库水间的耦合作用,从而给滑坡体灾害动力学特性研究带来很大误差甚至错误。运用滑坡灾害动力学、流体力学及流-固耦合理论,从灾害全过程角度揭示水动力环境下滑坡体渐进破坏、启动、高速运动、到涌浪形成、传播与爬坡灾害链效应,是进行滑坡涌浪灾害研究的关键。
基于先进的数值计算分析方法,从滑坡涌浪灾害全过程的物理力学机制出发,构建多种方法的耦合(联合)分析,充分利用不同分析方法的优势,实现滑坡涌浪的不同阶段、不同过程的分析,对于深入揭示水动力环境下库岸滑坡动力学、涌浪灾害机理及灾害链效应,同时对于发展现代岩土灾害分析理论方法,及指导滑坡涌浪灾害防治具有理论和工程意义。
