基于逆向挤出的七孔发射药口模设计

2024-01-11刘欢欢张江波麻明阳马中亮

火炸药学报 2023年12期

刘欢欢,张江波,侯龙,麻明阳,马中亮

(中北大学环境与安全工程学院,山西太原 030051)

引言

传统的发射药等高聚物挤出模具设计普遍采用试错法,具有很大的经验性,而且生产周期很长,成本较高,适应性差[1-2]。发射药从模具挤出会发生黏性流动,离模膨胀[3]和挤出偏孔是使得发射药的实际截面尺寸与挤出口型尺寸不符的主要原因,也是导致口型设计困难的主要原因之一[4]。

因为发射药的流动过程符合高分子聚合物的流动特征[5-8],为了研究发射药在模具挤出过程中的流变状况,很多研究者使用Polyflow[9]对发射药进行了挤出模拟。王倩等[10]模拟计算了单孔和七孔发射药流道内的速度和压强分布,讨论了药料黏度、松弛时间、入口体积速率等因素对流道内药料流动参数的影响;张丹丹等[11]试验验证了单孔发射药挤出模拟的准确性并利用Polyflow初步研究了3个单孔发射药同时成型及花边37孔发射药的挤出模拟;季丹丹等[12]采用Polyflow模拟了发射药模具收缩角、压缩段高度、成型段长度对挤出成型的影响并对模具进行了结构优化;分析了某高黏度19孔发射药模具压缩比、成型段长度和针架结构对挤出的影响[13];朱春鸠等[14]建立了考虑壁面滑移修正的发射药流动的数学模型,提高了数值仿真的精确度。大多研究者是通过调整收缩角、压缩段长度,成型段长度等进行直接挤出模拟来优化模具结构,对发射药挤出过程中存在的偏孔问题关注较少。有研究表明发射药偏孔会使发射药的燃烧渐增性变差、装药的初速温度系数和装药量增加,最大膛压降低,最终影响到其弹道性能[15]。因此本研究尝试通过逆向挤出模拟设计发射药模具的口模形状。

为了得到所需的挤出物形状而预测所需的模具形状即为逆向挤出。逆向挤出模拟在塑料橡胶等高分子聚合物的模具设计领域已取得了广泛研究。薛平等[16]对工字形木塑异型材料的口模进行逆向设计和分析,论述了Polyflow逆向数值计算在口模设计上的合理性;Y.K.Dai等[17]通过逆向模拟设计出汽车橡胶EPDM密封件的挤出模具,并对其进行了试验验证;姜波等[18]针对轮胎胶料的挤出胀大现象,通过逆向数值计算得到挤出口型,并使用正向仿真验证了其合理性;Sujit Sharma等[19]对汽车上一种复杂橡胶进行了正向挤出模拟和逆向挤出模拟,比较得出逆向挤出模拟比正向挤出模拟在口模设计上更加有效。发射药实际也是一种高分子材料,因此逆向挤出模拟也可用于发射药的口模设计。

本研究为了改善发射药挤出后的偏孔问题和探索逆向挤出的可行性,以七孔发射药为例进行了正向模拟与逆向模拟,研究药料在模具中的流动状况并分析了偏孔原因,并通过逆向模拟设计了模具口模形状,从模拟上验证了逆向挤出设计的口模有望改善发射药的挤出偏孔,以期为更复杂的多孔发射药的挤出偏孔问题提供另一种新的解决思路。

1 模型建立及求解

1.1 数学模型

流体的流动过程可以看作是无数质点的运动过程,因此也遵循运动过程的三大守恒定律:能量守恒定律、动量守恒定律和质量守恒定律,在此基础上推导出聚合物流体运动的基本微分方程:连续性方程、动量方程和能量方程[4]。

(1)连续性方程:

假设流场中某一区域流体的质量为M,g;体积为Ω,cm3;密度为ρ,g/cm3,则:

(1)

根据质量守恒定律可得到:

(2)

式中:∇为哈密尔顿算符;v为速度,m/s。

假定被积函数连续并且流体不可压缩可简化为:

∇·v=0

(3)

(2)动量方程:

流体在流动过程中动量的变化同样遵循动量守恒定律:流体中的任意体积微元单位时间内增加的动量等于同体积微元在单位时间内的受力总和,由此得出:

(4)

式中:P为流动方向上的压力,Pa;τ为应力张量,Pa;g为重力加速度,N/kg。

(3)能量方程:

根据能量守恒方程:总能量=动能+内能。假设流体不可压缩,在体积内没有热源时,能量方程的张量表达式为:

(5)

式中:Cp为流体的比热容,J/(kg·℃);D为形变速率张量,s-1;k为导热系数;T为开尔文温度,K。

1.2 流变模型

本试验中的药料为棉溶比1/1.35的单基发射药,使用MLW-400流变仪(长春市智能仪器设备有限公司)测出药料的流变数据。图1为25℃时药料的流变曲线,由图1可知,药料的黏度随剪切速率的增大而减小,表现出更接近假塑性流体的特征。选择Bird-carreau law模型[11]对流变数据进行拟合,其聚合物的黏度与剪切速率关系如下:

(6)

图1 药料流变曲线Fig.1 Rheological curves of propellant paste

对发射药流变数据进行拟合,拟合结果:η0=3.0584×105Pa·s,η∞=1Pa·s,λ=5.0s,n=0.188

1.3 几何模型

图2为使用Unigraphics NX软件[10]建立的七孔发射药的挤出模具模型,模具主要由模腔、模针、针架组成,图中模具主要结构参数为:压缩段长度L1=12mm,成型段长度L2=36mm,模针间距L3=2.8mm,模具入口直径D1=30mm,成型段截面直径D2=10mm,模针直径d=1mm。

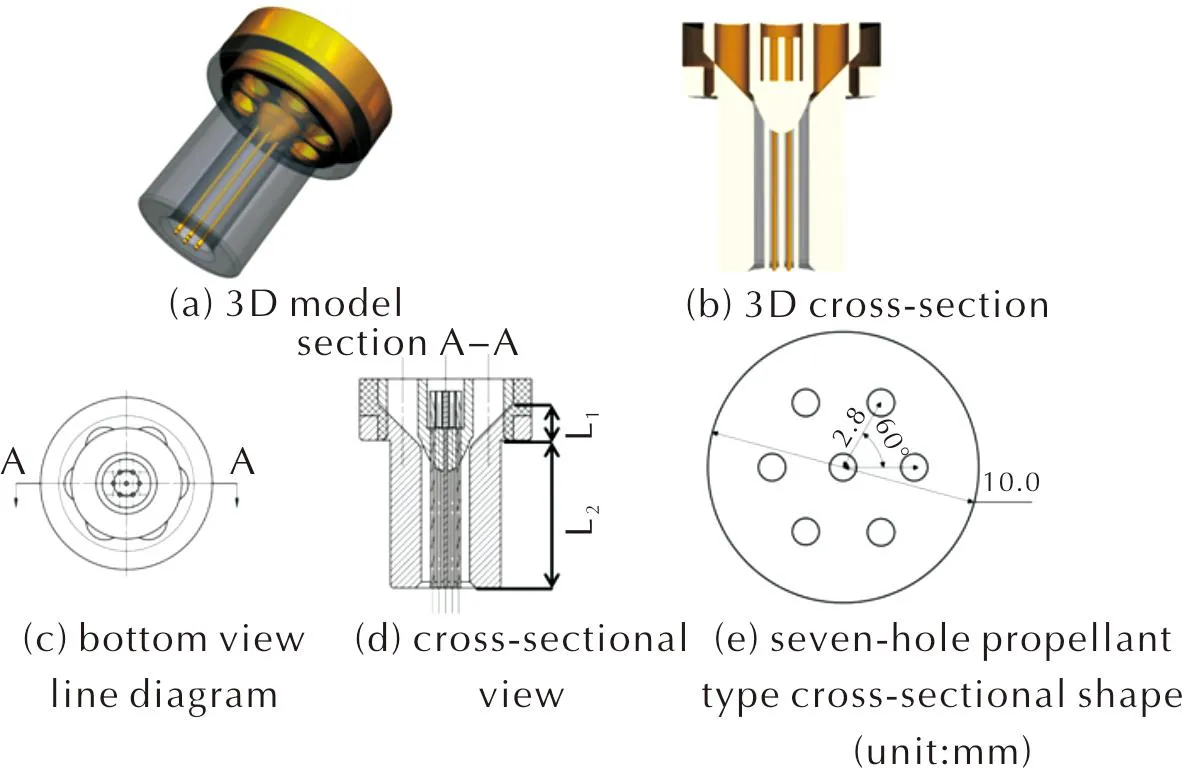
图2 七孔发射药挤出模具Fig.2 Extrusion die of seven-perforated propellant

1.4 网格划分

发射药的内流道模型主要包括压缩段、成型段和自由段。由于压缩段对偏孔变形的影响最小,可以忽略不计[20],为简化计算,根据七孔发射药的模具对内流道的成型段和自由段进行建模并划分网格,如图3所示。

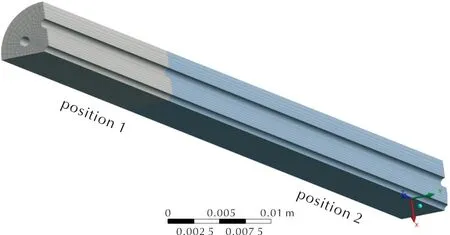
图3 七孔发射药网格划分Fig.3 Seven-perforated propellant meshing

在数值计算中,可根据几何模型的形状对模型进行简化,如对于对称模型只用计算其一半,由这一半的结果对称得到整个结果,可大大减少计算时间,提高计算效率。因为七孔发射药为高度对称几何体,表面粗糙度Ra为1.5。为简化计算,取模型的1/4进行网格划分并进行计算,由图3可知,利用Meshing进行网格划分,共包含127032个节点,110209个单元。网格为六面体主导,部分区域用四面体网格填充,形状规整。网格的单元质量平均为0.85、偏度平均为0.21,说明网格质量较高。计算区域由区域1和区域2组成,其中区域1长36mm,为模具内接触壁面的流体区域,为成型段;区域2长80mm,为模具外自由表面的挤出物区域,为自由段。

1.5 边界条件

边界条件类型包括:流动入口Inflow、作用法向速度和切向速度Normal and tangential velocities imposed、作用法向力和切向力Normal and tangential force imposed、作用法向速度和切向力Normal velocities and tangential force imposed、作用法向力和切向速度Normal force and tangential velocities imposed、对称面Plane of symmetry、自由表面Free Surface、流动出口Outflow、滑移边界条件Slip Conditions等。结合实际情况,七孔发射药内流道模型的边界如图4所示,结合实际情况设置如下边界条件:

图4 内流道边界Fig.4 Inflow channel boundaries

边界1:流动入口Inflow。设置入口体积流速Q=2×10-8m3/s。

边界2:模具壁面。假设壁无滑移vS=0,vn=0。

边界3:对称面。Plane of symmetry,fS=0,vn=0。

边界4:自由表面。Free Surface,指定边界2和边界4的交界面为自由表面的初始位置;并定义自由表面出口。

边界5:流动出口。作用零法向力和零切向力fS=fn=0。

1.6 基本假设

根据七孔发射药的药料流变性,在计算时做出以下假设:(1)用于模具中挤出的七孔发射药药料为不可压缩的高黏度非牛顿流体;(2)药料在模具中流速较慢,采用恒温药缸使其为等温流动,且与壁面无滑移;(3)药料在模具中流动为等温稳态层流流动,且在流道中全充满;(4)由于药料的黏度很大(约为1×105Pa·s),相对于黏性,重力和惯性的影响很小因此忽略。

2 仿真结果及分析

2.1 内流道的正向挤出模拟

使用正向模拟计算能够很好地预测药料在模具中的流动情况,通过研究药料在模具内的流动情况为模具的改进提供支撑,并能预测挤出物的挤出形变,挤出结果如图5所示。图5(a)～(e)分别为直接挤出药料流动过程中的速率、压力、黏度、剪切速率、流线等变化图,图中标尺由大到小用颜色由红至蓝表示,即红色区域表示最高的流速、压力、黏度、剪切速率、速度矢量;蓝色区域表示最小的。直接挤出模拟预测出了发射药的挤出形状,如图5(f)所示,填充的绿色实体表示挤出发射药的横截面,黑色轮廓即模具出口的横截面,由图5(f)可以很明显看出,发射药经模具挤出后出现了胀大与偏孔、除中心位置的圆孔外,其余圆孔的形状都发生了明显形变,变为椭圆形。在挤出过程中,流速均匀性是挤出的关键[21],因此重点对内流道的流速进行分析。

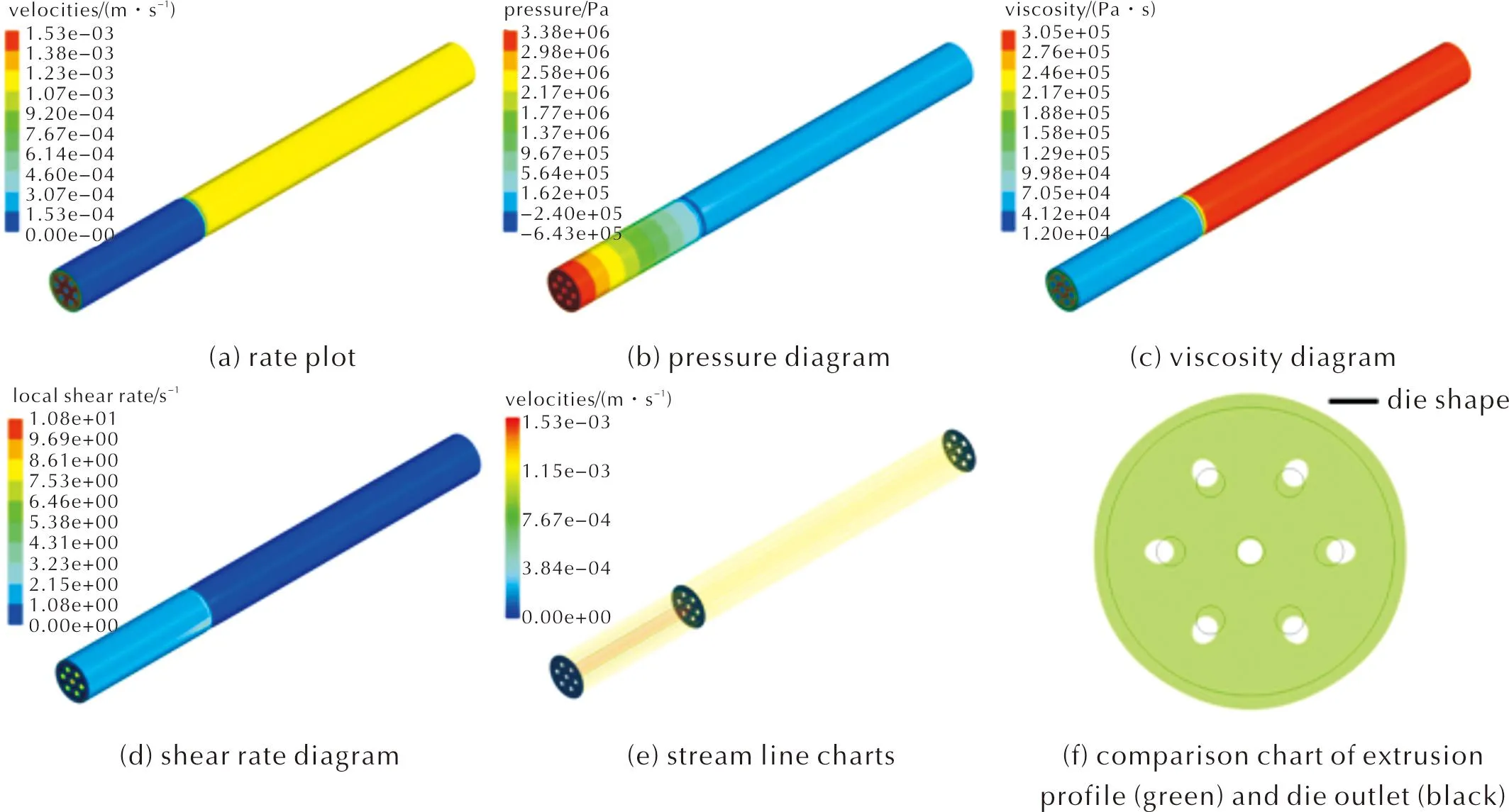
图5 挤出结果Fig.5 Extrusion results

在流体中心平面内插入曲线1～曲线6见图6(a),输出每条线上的流速如图6(b)所示。可明显得出挤出过程流速变化规律,呈现如下特点:同一水平截面药料流速由中心处至边缘呈梯度下降,越靠近壁面模针处流速越低,最大流速约1.53×10-3m/s,最小约为1.02×10-3m/s,最大流速约为最小流速的1.5倍;成型段内同一直线上的流速几乎不变(图中Z=0～3.0×10-2m);流速变化存在一个过渡区,过渡区约在Z=3.1×10-2～4.1×10-2m即模具出口前的0.005m和出口后的0.005m之间。此区间内不同位置的流速达到一致,约为1.15×10-3m/s,形变基本完成。

图6 流速曲线Fig.6 Flow velocity curve

2.2 内流道的逆向挤出模拟

虽然通过构建的内流道模型进行正向挤出计算可以求解出药料的流动状况来预测产品的出口形状,通过反复改变模具结构使挤出产品口型达到预期,但这样的过程需要耗费大量的时间精力,且效果并不一定理想。使用逆向挤出模拟有望很好地解决这一困扰。两种模拟的示意图如图7所示。

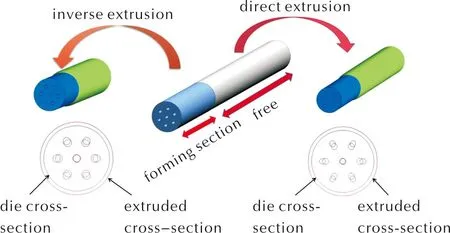
图7 逆向挤出(左)与正向挤出(右)对比示意图Fig.7 Schematic diagram of inverse extrusion(left) and direct extrusion(right)

逆向挤出的原理类似于正向挤出,区别在于正向挤出是根据模具的形状预测产品形状,即入口形状已知,预测出口形状;逆向挤出根据产品形状预测模具形状,出口形状已知且固定,预测入口形状从而到达设计模具口模的目的。在实际应用中对发射药内流道模型进行如图3所示同样的网格划分和边界条件设置,区域1为模具内流体,区域2为模具外流体。除此之外还需要进行如下不同设置:

(1)定义自由表面出口。单击Kinematic condition菜单栏中的Outlet(Inv.Prediction),选择边界5为自由表面的出口。

(2)设置完边界条件后,返回子任务设置菜单,点击Global remeshing(整体网格重置)定义网格重置方法。

(3)设置逆向分析。点击Inverse prediction management(逆向预测管理)→Enable inverse extrusion(使用逆向挤出)。随后返回主菜单。

(4)区域1网格重置。网格重置技术适用于存在自由表面或移动界面的问题,由于自由表面或移动界面处的网格会因为自由表面位置的变化而发生变化,而网格重置技术可以根据边界点的位置变化重新定义内部网格节点,点击1-st local remeshing命令,选择区域1,再选择Optimesh-3D(extrusion only)作为网格重置方法,然后在打开的界面中,选择不同的边界为网格重置的入口与出口。

(5)区域2网格重置。点击 Creation of a local remeshing(创建新局部网格重置),选择区域2为网格重置区域,选择Constant section for prediction选项作为网格重置方法。

通过这些设置,将模具外挤出流体的网格形状固定,再根据流体的流变性进行逆向计算使本该固定的模具内流体的网格进行收缩或膨胀,以达到设计模具的形状的目的。

挤出结果如图8所示。分别为逆向挤出药料流动过程中的速率、压力、黏度、剪切速率、流线等变化图,图中标尺由大到小用颜色由红至蓝表示,红色区域表示最高的流速、压力、黏度、剪切速率、速度矢量;蓝色区域表示最小的。图8(f)中黑色轮廓为针对挤出偏孔逆向补偿设计的口模,蓝色填充物代表药料的挤出形状。

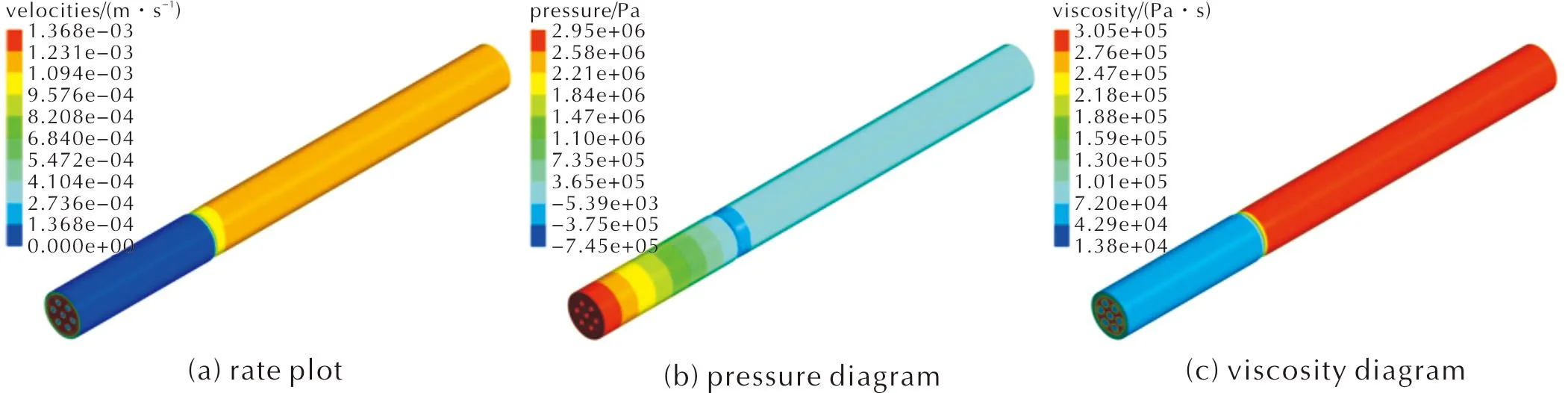
图8 挤出结果Fig.8 Extrusion results

2.2.1 流速分布

为了更细致地研究药料在模具中的流动变化及产生形变的原因,在挤出结果的中心面处即模针附近插入一平面如图9(a)所示,模针内外两侧的流速如图9(b)所示。在水平平面上由内而外做6条直线1～直线6,见图10(a)。其中线段1～线段3在模针的内侧,之间间隔0.0005m,线段4～线段6在模针外侧,同样间隔0.0005m,线段6在壁面处,绘制线段1～线段6的流速曲线如图10(b)所示;图11为入口处流速分布等线图;结合图9(b)、图10(b)以及图11可以看出,药料在模具内挤压过程中(即从Z=0到Z=0.036m的过程中)流速较为均匀,模针内侧的流速基本维持在1.36×10-3m/s附近;外侧流速维持在1.17×10-3m/s附近,壁面处流速约为1.0×10-3m/s;并在模具内挤压过程中变化不大,但不同位置的流速分布并不均匀,靠近壁面及模针处流速小,模针内侧的流速基本大于模针外侧流速,同一截面流速的不一致是导致挤出形变的重要因素。挤出模具后在0.005m内流速均降落在1.10×10-3m/s;壁面处上升至1.10×10-3m/s,这个区间为挤出后的过渡区,此区间过后流速基本不再变化。

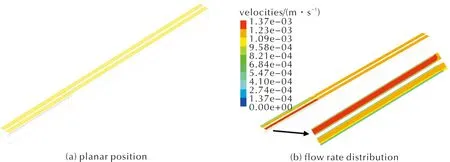
图9 平面上的流速分布Fig.9 Flow velocity distribution on a flat surface

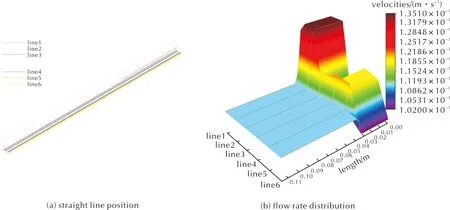
图10 线段1～线段6不同位置的流速对比Fig.10 Comparison of flow rates at different positions of line 1—line 6

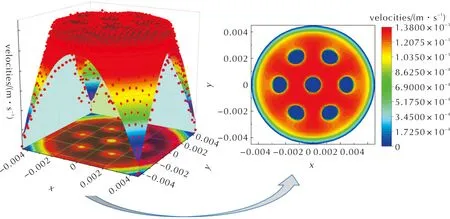
图11 逆向挤出入口流速等线3D图Fig.11 Inverse extrusion inlet flow velocity isoline 3D plot

2.2.2 压力分布

图12为流道中心平面上线段1～线段6的压力曲线,结合图10(b)与图12可发现药料在模具中的压力变化规律:同一水平截面处的压力几乎一致;入口处压力达到整个挤压过程中的最大值,约为2.9×106Pa,在此后挤压过程中呈现线性下降趋势;药料挤出模具后,自由段的药料不再收到挤压作用,压力降到0趋于稳定,整个挤压过程压力变化较为规律。

图12 压力曲线1～线段6Fig.12 Line 1—line 6 pressure curve

2.2.3 剪切速率分布

挤出过程中药料入口处的剪切速率分布如图13所示。由图13中左侧3D示意图可明显看出,挤压过程中药料在壁面与模针处的剪切速率较大,其中越靠近模针处剪切速率越大,最大处剪切速率在8.520s-1以上,入口处除模针与壁面处外,其余区域剪切速率梯度较小。图14为整个挤压过程中1/4内流道药料的剪切速率分布。由图14可知,中心处模针相较于外侧模针的剪切速率更大,颜色为红色,剪切速率约为9.023s-1;并且还可看出整个挤压过程中同一位置的剪切速率几乎与其入口处的剪切速率保持一致,因此剪切速率的变化可能对挤出偏孔的影响较小。

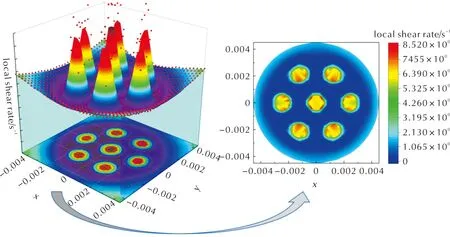
图13 逆向挤出入口处剪切速率等线3D图Fig.13 Isolinear 3D plot of shear rate at inverse extrusion inlet

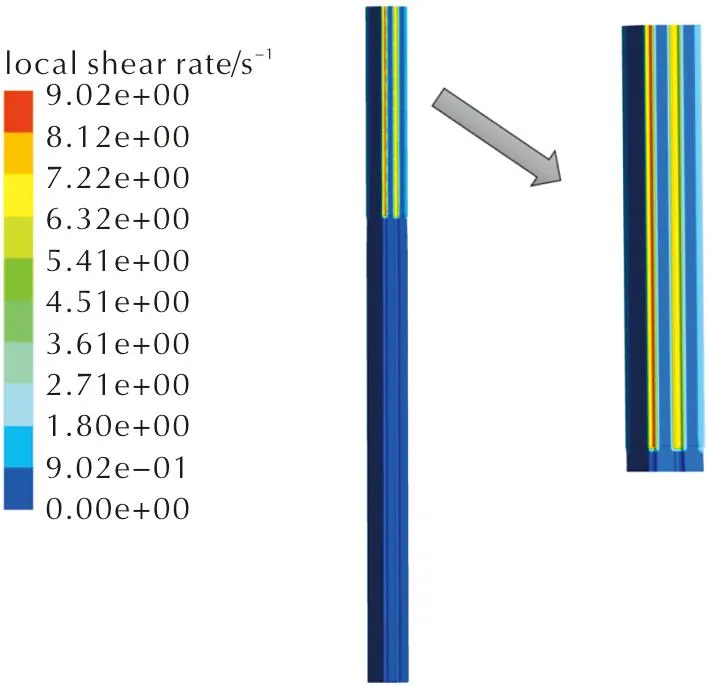
图14 内流道剪切速率分布Fig.14 Internal channel shear rate distribution

通过分析逆向挤出过程中流速、压力和剪切速率分布规律,得出在挤压过程中相较于压力、剪切速率,流速的分布不均可能对于挤出形变的影响更大。根据模具入口处截面的速度分布可以看到药料入口处的流速分布是不同的,靠近壁面处流速低,模针与模针之间流速高。药料离开成型段后在过渡区中不再受到模具壁面的约束且同一截面的流速还未达到一致,根据伯努利定理,流速大的地方压强小,流速小的地方压强大,压强的不同导致药料外形和孔发生变形。挤出末端流速变为恒定值,离开模具后大部分区域流速变小,其中流速快的部分因为流速降低导致面积增加,流速慢的区域因为流速增大导致面积减小,速度的重新分配引起自由表面的挤出变形。

虽然在挤出过程中很难人为地对流速进行控制,但是通过逆向数值计算对挤出后形变的区域在模具中进行逆向的补偿设计。设计后的模具口形如图15所示,黑色轮廓为逆向挤出设计的口模,与原来形状相比,原来的面积为73.0420mm2,设计后的面积变小,为67.8468mm2,以补偿发射药离开模具后的膨胀;同时设计后的模针间距约为2.43mm,模针也由圆形设计为不规则的扁圆,并与图5(f)中直接挤出后的椭圆形内孔方向相反,同样是为了补偿挤出后的内孔形变。

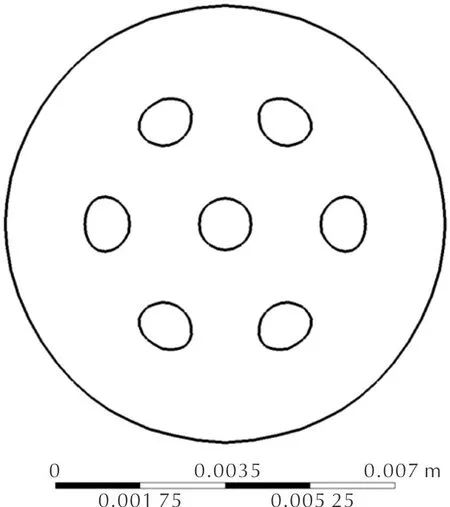
图15 设计后的模具口形Fig.15 The shape of the die mouth after design

2.3 挤出模拟验证

使用UG或其他建模软件打开Ansys Polyflow生成的口模文件(IGES文件),根据设计后的口模建立修正后的发射药内流道模型,划分网格如图16所示、设置同正向模拟同样的边界条件进行挤出模拟验证。

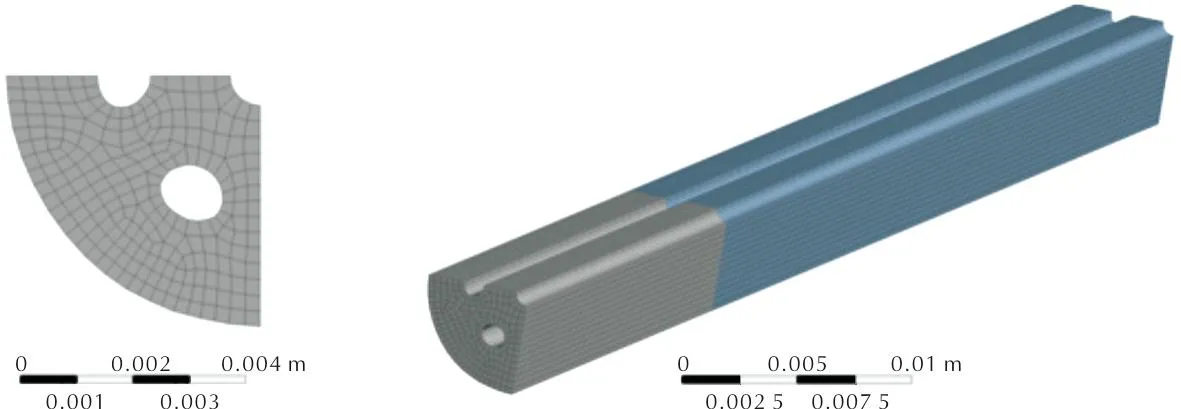
图16 网格模型局部视图(左)与整体视图(右)Fig.16 Mesh model partial view(left) and global view(right)

挤出后的结果如图17所示,其中黑色区域为挤出轮廓,红色线框为入口轮廓。由图17可以看出,修正后的口模挤出后虽然同样出现了挤出偏孔,但是偏孔后的孔形更趋近于圆形,与初始的挤出物[见图5(f)]相比更加规整,这是因为设计的口模形状虽然不能阻止发射药挤出偏孔这一行为,但是却能通过研究发射药挤出时在模具内的流动性掌握其偏孔规律使偏孔朝着理想的方向偏孔。从理论上证明了逆向模拟设计的口模对七孔发射药的偏孔问题具有改善作用,后续进一步改善边界条件等参数有望使挤出物更加规整。

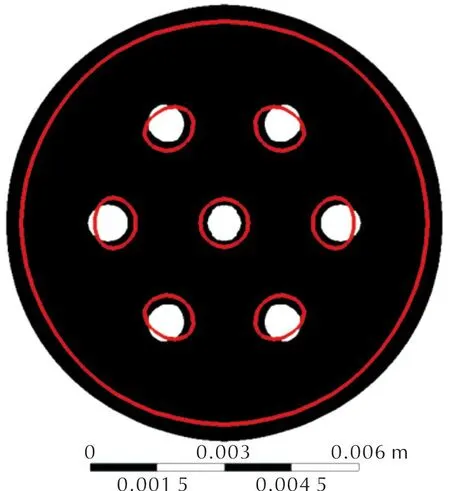
图17 挤出轮廓(黑)与入口轮廓(红)Fig.17 Extrusion profile(black) and inlet profile(red)

2.4 与试验结果的对比分析

将设计后的口模进行挤出试验,并与目标发射药进行对比分析,分析结果见表1。表1中序号1[20]和序号2[22]为七孔硝基胍发射药,模针间距挤出误差约为10%左右,序号3为使用逆向模拟设计后的模具挤出误差约为5.3%,使误差进一步缩小。也有研究者[23]针对19孔发射药使用试错法不断调整模针位置来优化挤出偏孔问题,虽然调整后的误差满足要求,但该过程需要耗费大量的精力来不断试错。使用逆向模拟有望能显著缩短该研究时间,提高研究效率。

表1 试验结果与设计目标的误差对比分析Table 1 Comparative analysis of the error between the test results and the design objectives

2.5 试验验证

使用目前常用的模具进行正向挤出试验,挤出结果如图18所示。

由图18可知,目前正向挤出的发射药仍有改进的空间,较容易出现偏孔、孔大小不均匀等问题,逆向挤出设计的模具有望提高发射药的挤出质量。但由于现有的实验条件以及药料均匀性、收缩率、溶剂含量等的影响,目前逆向挤出试验较难成功,但这一逆向挤出的思路有望对后续研究人员提供帮助,能够在更加成熟的条件下进行挤出验证,也希望能够对更复杂的发射药模具设计提供帮助。