基于储能的电力系统潮流协调优化控制策略

2024-01-11李美妍吴俊玲陆润钊秦晓辉

东北电力大学学报 2023年6期

李美妍,吴俊玲,陆润钊,秦晓辉,张健

(1．东北电力大学电气工程学院,吉林吉林 132012;2．中国电力科学研究院有限公司,北京 100192)

0 引言

在构建新型电力系统的背景下,风电、光伏等新能源的装机占比不断增高,以输送新能源为主的跨区直流输电支路容量也不断增加。一方面,新能源发电具有随机性和波动性等特点,使得新能源富集地区送出通道发生短时受阻;另一方面,大容量直流接入的送、受端电网在发生交、直流故障后,都将会引发大规模潮流转移,导致正常运行支路发生短时过载等问题,成为制约新能源发展和限制交直流输电能力的重要因素[1-4]。

为应对上述风险,规划和运行中采取的措施通常包括建设新的输变电设备、限制新能源的最大接入容量以及预控直流的输送功率等预防性措施或切负荷等紧急控制措施[5]。这些措施一方面制约了新能源的开发规模或降低电网设施的利用率,另一方面也对故障后运行方式的调整提出了更高的要求。在高比例新能源电网中,储能设备将大量接入[6-7],基于变流器控制的现代储能具有快速的双向功率吞吐能力,全功率响应时间小于100 ms,且目前大容量电力储能的时长可以达到数小时。因此,通过采用定制化的控制策略,电网中的储能设备不仅能参与系统全局的功率平衡,同时也能参与到局部电网的潮流控制中,解决新能源集中外送地区输送功率短时受阻或故障后局部断面短时过载等问题,对高比例新能源交直流混联电网的安全稳定运行和发展具有重要的实际意义。

目前,利用储能进行潮流控制的研究和应用较少。在传统的潮流控制方面,被广泛认可的控制算法主要有灵敏度法[8-11]和优化规划法[12-16]。其中,灵敏度法存储量小,计算简单且速度快,但需要多轮调整,并且在调整过程中可能会产生新的过载问题。优化规划法通过对数学模型的构建和求解,得到控制方案,最终消除支路潮流越限问题。文献[12]构建双目标模型,并通过遗传算法进行求解,确定控制方案。但缺少对控制设备的预处理,所需设备涉及系统所有可控机组。

本文为最大化的发挥储能的作用,以储能作为主要的潮流越限控制措施,将灵敏度法与优化规划法相结合,提出一种储能和发电机组合控制的潮流越限分散协调优化方法。首先,根据综合控制灵敏度优选可控储能点,同时考虑了储能可用功率和待调整支路的负载程度;其次,以总控制代价最小为目标,建立系统总调整量最少和总控制节点数最少的优化模型,并采用大M法进行线性化处理;最后,基于改进的IEEE RTS24节点系统进行仿真验证,验证所提措施的有效性以及方法的合理性。

1 待调整支路和可控储能节点的确定方法

1.1 待调整支路集

待调整支路集指由网络中各支路出现重载或过载情况的支路所构成的集合。本文通过计算网络中各支路的负载率,确定待调整支路集。负载率指标为

(1)

设支路安全监测阈值为γ,根据公式(1),通过此时的潮流分布,计算各支路的负载情况,确定过载支路集合SL1和重载支路集合SL0。

(2)

其中,γ的取值决定了对重载支路的监测范围,通过设定γ值的大小,适当扩大对重载支路的监测范围,能够尽可能的减少在控制过程中支路发生新的过载问题,有助于优化计算收敛;待调整支路集合为SL=SL1∪SL0。

1.2 可控储能节点集

虽然系统中每一个可控储能节点都可以对支路潮流进行控制,但是针对于某一特定支路,不同节点的控制效果不同。因此,应选择控制效果较好的可控储能和发电机节点进行控制,既降低了控制策略的复杂性,也提高了计算效率。

在电力系统中,当控制节点的功率调整量为单位功率时,电网中各支路的有功功率变化量即为控制节点对各支路的功率控制灵敏度。功率控制灵敏度计算公式如公式(3)所示。

(3)

公式中:SL,i为控制节点对支路L的功率灵敏度;ΔPi为控制节点的出力调整量,ΔPL为被控支路功率变化量。

节点对支路的控制效果不仅与功率控制灵敏度有关,还与该节点的可用功率有关。当节点注入功率增加时,将各支路感受到的功率变化量定义为支路所受到的冲击。记各可控储能节点对支路的冲击能量为

(4)

公式中:i为储能节点;ΔPi_C_max为储能节点i的最大可调充电功率;ΔPi_DC_max为储能节点i的最大可调放电功率;SLk,i为储能节点i对支路k的功率控制灵敏度。由CLk,i可知,储能i的可调功率越大,支路k感受到的冲击能量就越大。

在实际电网中,由于系统规模庞大,储能电站与网络支路数量众多,有必要根据控制效果对参与潮流控制的储能设备进行初步筛选。为此本文基于上述冲击能量的概念提出储能对各待调整支路的综合控制灵敏度的计算方法。

根据待调整支路集合中各支路的重载程度计算各支路的权重系数,如公式(5)所示。

(5)

则综合控制灵敏度表达式为

XLk,i=CLk,iHLk

(6)

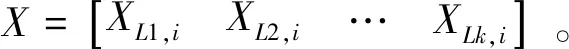
即节点i的综合控制灵敏度记为

(7)

为了优化控制节点数,可以根据综合控制灵敏度的大小对控制效果较弱的节点进行剔除。

2 基于储能的电网潮流控制优化模型

2.1 目标函数

基于储能的支路潮流优化控制目标是在各控制措施中选择使系统稳定且控制代价最小的控制组合[17-19]。潮流控制采取储能的有功功率出力调节,发电机机组平衡出力,最终实现系统功率平衡,进而阻断支路潮流越限。采用大M法[20-22]转化后的多目标线性优化模型为

(8)

其中,

(9)

(10)

公式中:F为过载控制的总控制代价;n和m分别为参与控制的储能电站数和发电机机组数;CS为储能单位容量控制成本;CG为发电机单位容量控制成本;ΔPSi为储能节点i参与控制的调整量;ΔPGj为发电机节点j参与控制的调整量;Δt为储能参与控制的时间,可根据潮流越限的场景需要确定;Ii和Ij为状态变量,分别表示储能和发电机的启停状态;M为发电机参与控制的惩罚系数,当M为一个极大的正数时,储能出力的优先级高于发电机出力的优先级。

其中,CSk表示为储能参与控制的惩罚系数,代表了调用储能电站的通信成本、寿命损耗以及运行维护成本、回收价值等,惩罚系数的大小制约了参与控制的储能电站的数量。

2.2 约束条件

为了避免在调节过程中可控节点控制量不足、产生新的支路越限等情况,优化规划需要考虑保证系统稳定运行的各类约束条件。

2.2.1 节点注入功率约束

储能的充放电约束

-Pess_i_max≤Pess_i≤Pess_i_max

(11)

(12)

(13)

公式中:Pess_i为储能机组i的功率值;Pess_i_max为储能机组i的最大充放电功率;SOC0为储能初始荷电状态;Δt为持续时间;E为储能存储的总能量;SOCmin一般取0.1～0.2,SOCmax一般取0.8～0.9。

发电机出力约束

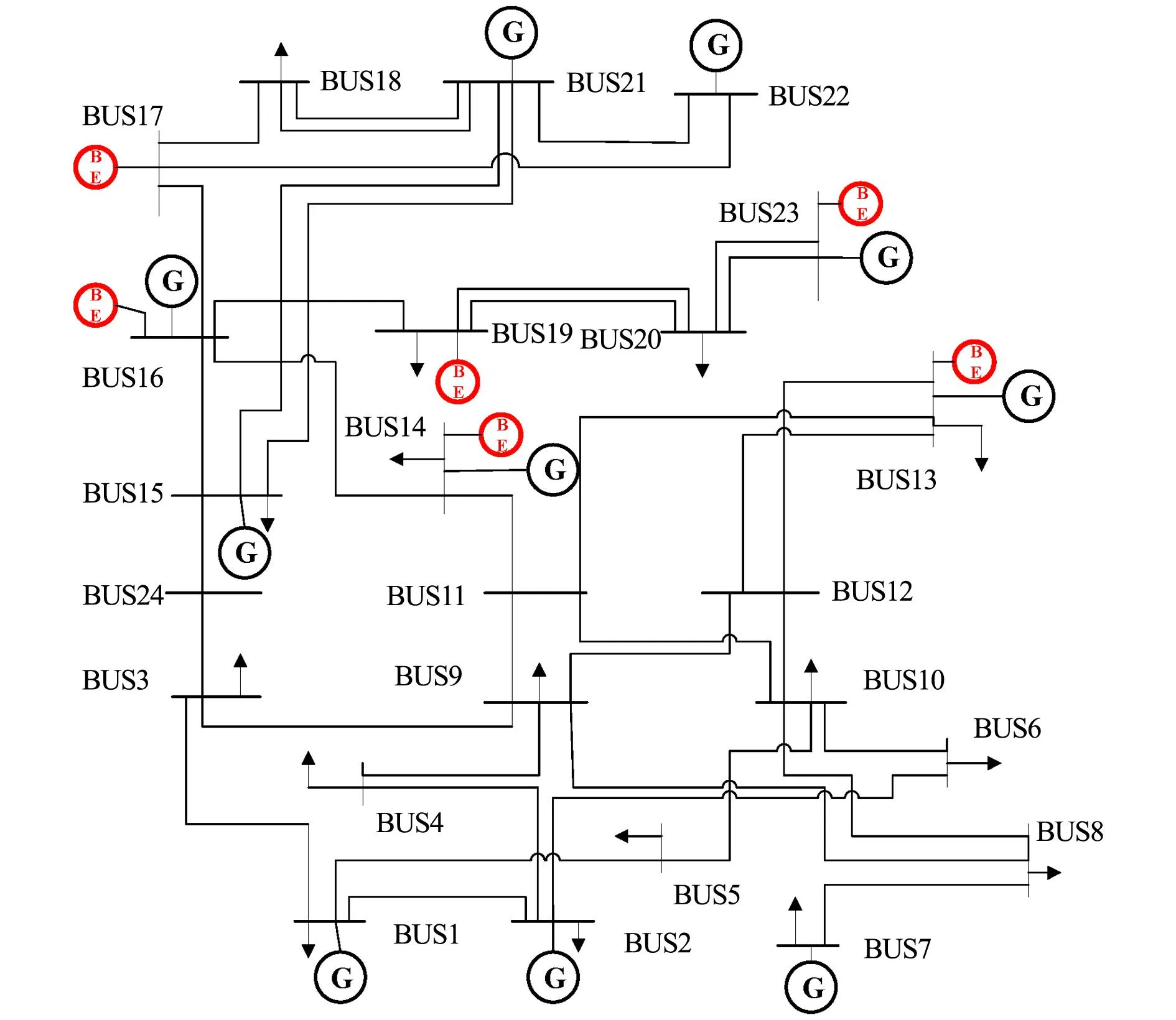
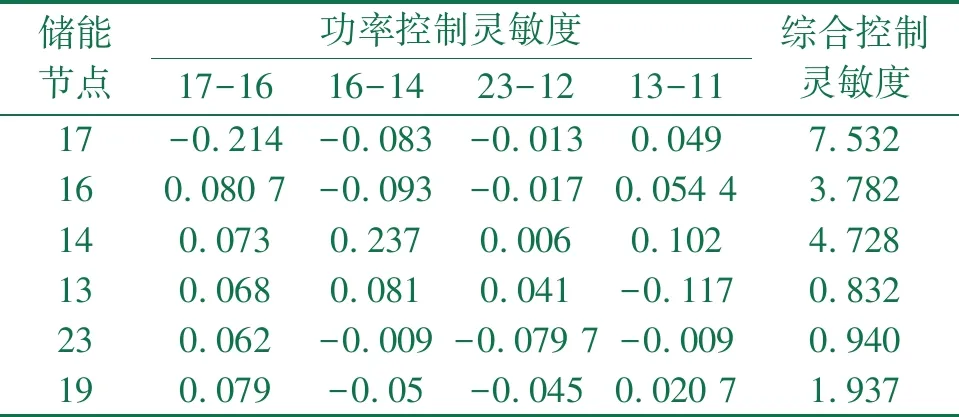
PGj_min-PGj<ΔPGj

(14)

公式中:PGj为发电机j当前的有功功率出力值;PGj_max为发电机j的最大有功功率出力值;PGj_min为发电机j的最小有功功率出力值;

2.2.2 支路最大传输功率约束

对于系统中的任意支路L,满足约束

PL+ΔPL≤ηPLmax

(15)

公式中:PL为支路L的有功功率初始值;ΔPL为控制后支路L有功功率的变化量;η为支路安全阈值。

2.2.3 系统功率平衡约束

储能放电时的功率平衡约束:

(16)

储能充电时的功率平衡约束:

(17)

公式中:PG,i为节点i处电源的有功功率;PS,i为节点i处储能充放电功率;PL,i为节点i的有功负荷;θ为节点电压相位角;Bij为支路导纳矩阵的虚部。

2.2.4 节点电压和相角约束

节点电压幅值约束

Ui_min≤Ui≤Ui_max

(18)

公式中:Ui为节点i的电压值;Ui_max和Ui_min分别为节点i允许的最大和最小电压值;

支路首末两端相角约束

(19)

公式中:θij为支路两端的初始相角差;Δθij为越限控制后支路相角差的变化量;θij_max为允许支路两端相角差的最大差值;

3 算例分析

为验证本文方法的有效性,采用仿真工具MATLAB基于改进的IEEE RTS24节点系统进行仿真分析,接线图如图2所示。该系统共有6个储能电站,分别接入节点14、16、17、19、13和23;6台发电机,分别接入节点1、2、7、15、21和22。根据前文所提方法和模型,对系统支路潮流越限进行控制,并对结果进行分析。以电池储能为例,储能的单位功率成本(CS)为0.52元/kW·h,发电机单位功率成本(CG)为0.26元/kW·h,惩罚系数M和CSk分别取1 000和2 000。储能和发电机节点的初始状态,如表1和表2所示。

图1 改进的IEEE RTS24节点系统

表1 储能节点的功率

表2 发电机节点的功率

系统中支路15-21因故障从系统切除后,将使系统潮流重新分布,导致支路17-16和16-14出现不同程度的越限。根据公式(1)计算潮流转移后各支路的负载率,结合公式(2)确定待调整支路集合,表3为待调整支路集信息,其中,安全监测阈值取0.9,安全阈值取0.95。根据公式(3)计算各储能对待调整支路的功率灵敏度如表4所示。

表3 待调整支路集的信息

表4 待调整支路的灵敏度

为了验证所提综合控制灵敏度方法的合理性,将该方法确定的控制节点集与优化所确定的控制节点集合进行对比分析。根据公式(6)计算综合控制灵敏度,以剔除总控制节点的40%为例,将综合控制灵敏度较小的储能节点进行剔除,确定储能节点的最优控制集。如表2所示,剔除综合控制灵敏度较小的储能节点为13和23,因此,确定最优控制节点集合为[17 14 16 19]。

根据公式(7)给出的优化模型,求解得到支路潮流越限调整方案以及调整效果,如表5和表6所示。算例系统所示场景为故障后潮流短时越限的场景,储能参与控制时间取30 min。由表5可知优化确定的控制储能节点集合为[17 14 19],因此,优化确定的可控储能节点集为综合控制灵敏度法所确定可控储能节点集的子集合。同时,剔除控制效果较弱的储能节点后,优化时间较未剔除节点的优化时间提高了12.2%,说明该方法的优化策略是合理的。

表5 调整方案

表6 调整效果

表6所示的调整结果验证了本文所提控制措施的有效性。越限支路17-16和16-14的负载率分别由1.028和1.041降至0.95,且重载支路负载率均在安全监测阈值内。

为了说明本文所提方法的优势,将前文所提目标函数的优化(A)与单一目标函数的优化(A1:总控制调整量最小)进行对比分析,表7和表8分别给出了以A1为优化目标的调整方案和调整效果。由表8可知以A1为目标函数的优化控制仍可解决支路潮流越限问题,但将两种目标函数的优化结果进行对比如表9所示,以A为目标函数的优化控制经济性更高。根据表9可知,如果以A1为目标函数,总控制调整量较以A为目标函数的控制调整量仅降低了0.519 MW,但是以增加两台储能参与控制为代价,且部分储能的调整量很小,降低了经济性。与单一目标函数的优化控制相比,本文所提目标函数的优化控制能在实现控制调整量最小的同时使参与调整的节点数最少。