基于SA-RF的公路隧道交通流数据修复模型研究
2024-01-10付立家陈丽阳
付立家, 陈丽阳, 尚 康
(1.招商局重庆交通科研设计院有限公司, 重庆 400067; 2.重庆交通大学 交通运输学院, 重庆 400074)
公路隧道配备了大量机电设施和交通感知设备,以全方位获取隧道交通信息、环境信息和结构信息,为公路隧道智能化管理和控制提供数据支撑。但因隧道运行环境复杂、设备检查维护不及时、通信质量不稳定等因素,或多或少导致隧道交通流数据缺失,降低了数据的完整性和准确性。为解决此类问题,对隧道内环境、交通状态等各类运营数据进行实时、完整获取并深入挖掘,以提高应急处置能力,实现运营安全预警[1],需对交通流缺失数据修复方法开展研究,为公路隧道运营管理提供稳定的数据保障。目前,针对缺失数据的修复方法主要包括统计学方法和机器学习方法,前者包括EM(Expectation Maximization)填充算法[2]、回归分析法[3]、多重插补[4]等,但因该方法未考虑数据类别的差异性,致使修复效果精度较低;机器学习方法是以分类、聚类和回归方法修复缺失数据集,主要包括KNN(K-Nearest Neighbor)算法[5]、K-means算法[6]、贝叶斯网络[2,7]、支持向量机SVM(Support Vector Machine)算法[8]和随机森林RF(Random Forest)算法[1,9]等,该方法在交通领域研究与应用较多。邵毅明等[9]在随机森林模型基础上采用遗传算法进行优化调参;曾小华等[10]采用插补缺失与神经网络集成方法预测修复公交客车行驶工况的缺失数据;张壮壮等[11]采用时空卷积神经网络预测模型,从时间和空间相关性预测修复路网交通流数据。上述预测修复方法主要从时间、空间相关性的视角进行修复,而从时空相关性视角针对交通流数据的缺失率和缺失模式研究报道较少。
为此,本文从时空相关性视角,建立基于SA-RF的公路隧道交通流缺失数据修复模型。根据数据缺失模式,先分别从时间相关性建立单变量修复模型和空间相关性建立多变量修复模型,然后将两者结合,建立时空相关性的综合修复模型,修复交通流数据的一般数据缺失模式,并在不同缺失率下验证修复模型的准确性和可靠性。
1 基于SA-RF的公路隧道交通流修复方法
RF模型中有许多重要超参数,而超参数的取值不同致使模型预测修复精度不同。为得到更精准的交通流预测修复模型,需对RF模型的参数进行多次调整,并训练和验证修复效果。传统方法如网格搜索法、随机搜索法等存在训练步骤复杂、时间长、效率低等问题,而模拟退火算法SA(Simulated Annealing)能够同时优化多个参数、避免陷入局部最优解、高效寻找最优参数。为此,本文以SA算法对RF模型的主要参数进行寻优,并根据最优参数建立SA-RF模型预测修复缺失交通流。
1.1 模拟退火算法SA
模拟退火算法[12-13]是借鉴固体退火原理的一种通用概率演算法。该算法需设定初始高温、降温速率和结束低温,在每阶段中,以固定速率降低当前温度,并判断是否以新解替换当前最优解。如果得到随机新解优于当前最优解,则以新解替换当前最优解;如果得到随机新解不优于当前最优解时,则以Metropolis准则的接受概率p判断是否接受新解替换当前最优解。其中接受概率p见式(1):
(1)
式中:Ci,Ci+1分别为目标函数在第i次和i+1次的迭代值;T为当前温度,在迭代过程中T值逐步缓慢减小,当T值变化太快,会使目标函数陷入局部极值点。
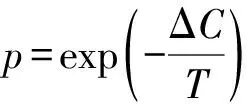
1.2 随机森林算法RF
随机森林是一种统计学理论,其基本思想是根据Bootstrapping重抽样方法依次建立多个分类或回归树,对多个决策树的输出结果进行集成,最终得到分类或回归预测结果。大量的理论和实证研究都证明了RF具有很高的预测准确率,对异常值和噪声具有很好的容忍度,且不容易出现过拟合[14]。
RF算法基本步骤:1) Bootstrapping重抽样,从训练样本数据中随机抽样一部分数据,用于训练决策树;2) 使用随机抽样数据构建决策树,包括ID3、C4.5、CART等算法;3) 计算决策树的每个预测结果,对于每棵决策树,根据特征的取值、分支条件等规则,将该样本划分到对应的叶子节点中;4) 计算RF结果,统计所有决策树中该样本所在的叶子节点的预测结果,按照预测结果的投票数或概率进行加权平均,得到最终的预测结果。
1.3 交通流修复方式
数据缺失模式大致分为单变量缺失、多变量缺失、单调缺失和一般缺失[15]4类,如表1所示。
在公路隧道采集的交通流数据中,缺失数据随机分布在不同属性之间,往往伴随着单变量和多变量缺失模式,符合一般缺失模式。因此将单变量和多变量修复模型相结合,从时空相关性构建基于SA-RF的综合修复模型,用于修复常见的一般缺失模式。

表1 缺失模式及修复方式
2 交通流修复流程
SA-RF修复模型主要包括数据处理模块、SA-RF参数寻优模块和SA-RF预测修复模块,流程如图1所示。数据处理模块是剔除异常值、缺失值、标准化处理、划分训练数据集和测试数据集;SA-RF参数寻优模块是以SA模型寻找RF模型4个主要参数,并确定最优参数组合,包括决策树个数(n_estimators)、决策树最大深度(max_depth)、节点可分的最小样本数(min_samples_split)和叶子节点含有的最少样本(min_samples_leaf);SA-RF预测修复模块是根据最优参数组合和训练数据集建立SA-RF交通流修复模型,预测修复交通流缺失值。
2.1 交通流数据处理模块
由于公路隧道采集的交通流存在异常值,为保障训练及测试数据集的完整性,在数据处理阶段剔除包含缺失和异常值的数据条。根据单变量和多变量修复模型划分对应的训练集和测试集,并训练SA-RF修复模型和参数寻优。
1) 单变量修复模型数据集
单变量修复模型是根据时间相关建立预测修复模型,在完整的数据集上,设定时间窗口的维度为k、步长为1,滑动提取交通流数据时间序列样本量为t+1,构建k×t维时间序列特征矩阵X和目标向量

图1 SA-RF修复流程
标签Y,见式(2)。
Y=[y1,y2…yk]T
(2)
式中:xij为第i个样本的第j维数据;yi为第i个样本的目标值;X为时间序列特征矩阵,即修复模型自变量;Y为目标向量标签,即修复模型因变量。
2) 多变量修复模型数据集
多变量修复模型是根据空间相关性建立预测修复模型,利用交通流各参数间非线性关系,以多变量预测方式修复交通流缺失数据。在完整数据集上,构建特征矩阵X,见式(2),其中k为交通流参数维度,t为交通流数据量,即采集样本量。
3) 修复模型训练集与测试集
为验证预测修复模型的修复效果,根据单变量和多变量修复模型数据集,以9∶1分别划分相应的训练数据集和测试数据集。其中训练数据集用于SA-RF模型的训练和参数寻优,测试数据集的目标向量标签Y需人为随机缺失部分数据,用于验证模型修复效果。
4) 误差函数
以均方误差(MSE)计算训练过程中损失值,表示预测值与真实值之间匹配度,计算公式如下:
(3)
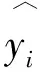
以平均绝对百分比误差(MAPE)衡量修复值与真实值间的相对偏差,计算公式如下:
(4)
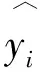
2.2 SA-RF参数寻优模块
单变量和多变量修复模型在SA-RF模型中训练方法相同,但训练数据集不同,导致不同的训练结果。按照图1的训练流程,将单变量和多变量修复模型训练数据集分别作为输入量训练SA-RF模型。在训练过程中以SA算法不断迭代优化,寻找单变量和多变量修复模型的最优参数组合。在寻参过程中以RF模型预测值与真实值的MSE作为目标函数,快速、准确寻求最优参数组合,整个过程是一个求解全局最优问题。
2.3 SA-RF预测修复模块
公路隧道采集的单条数据中会存在数据未缺失、单变量缺失和多变量缺失,因此,在实际应用中综合2种模式对缺失数据进行修复。通过训练数据集和最优组合参数对SA-RF模型进行训练,利用训练好的预测模型对缺失验证数据集进行修复,应用MAPE评估修复效果。以交通流参数的车流量(Q)、平均车速(V)和时间占有率(Oc)为参数,确定缺失数据综合修复步骤。
公路隧道部分检测数据如表2所示。表2中,缺失数据用null表示;t+2、t+3…t+n时刻为单变量数据缺失;t+5、t+n-1时刻为多变量数据缺失。单变量修复模型需满足该时间序列前k个数据未缺失,而多变量修复模型需满足待修复变量的其他变量数据均未缺失。

表2 缺失示例数据
SA-RF综合修复模型的修复步骤:1) 提取公路隧道交通流缺失数据,记录缺失时间Ti、缺失变量(Q/V/Oc),并存储在lose_data中;2) 判断lose_data中第i个交通流数据缺失类型(单变量缺失/多变量缺失);3) 根据缺失类型建立待修复特征向量Xi,单变量缺失根据Ti时刻其他变量数据建立待修复特征向量,多变量缺失根据前k个数据建立待修复特征向量;4) 以SA-RF预测修复值,多变量预测修复模型修补单变量数据缺失,单变量预测修复模型修补多变量数据缺失;5) 以修复值补全交通流缺失值,并删除lose_data中Ti时刻元素,若lose_data中元素个数为0,则完成所有缺失值修复,否则转回步骤2)。
3 实例验证
3.1 公路隧道交通流概况
为验证综合修复模型的准确性和可靠性,以重庆某公路隧道为研究对象,在同一时间和区域内持续收集交通流数据。采样时间为2021-07-02—2021-09-17,采样间隔1 h,共计采样1 848组数据,如图2所示。由于采样交通流数据存在异常和缺失问题,需预处理原始采样数据,包括剔除缺失值、异常值和标准化处理,同时按照9∶1划分训练数据集和测试数据集。训练数据集用于SA-RF参数寻优和训练修复模型;测试集划分3%、5%、10%和15%缺失比例,用于验证模型的准确性。

(a) 交通量
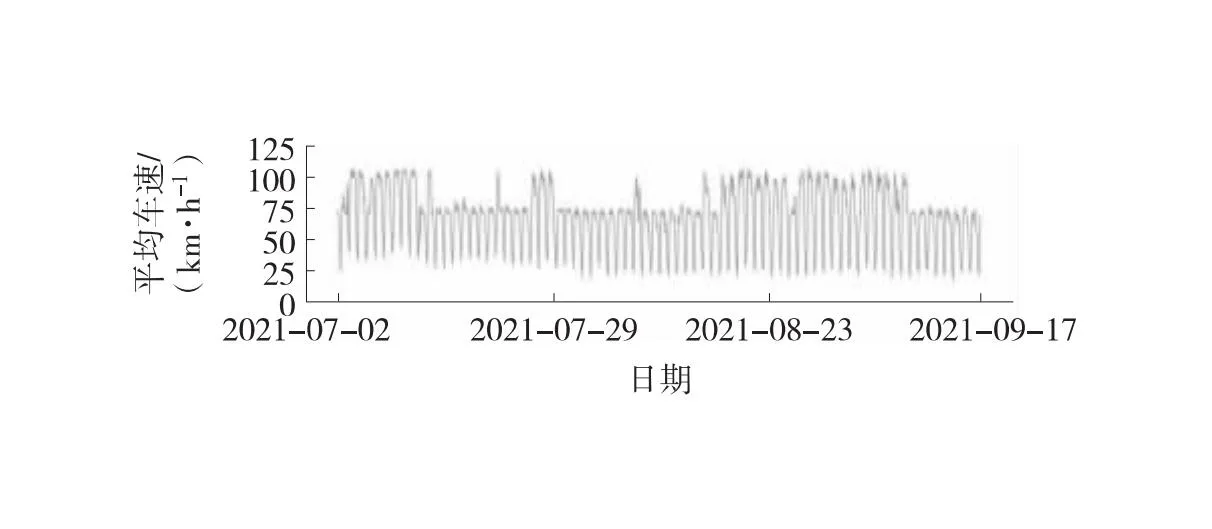
(b) 平均车速
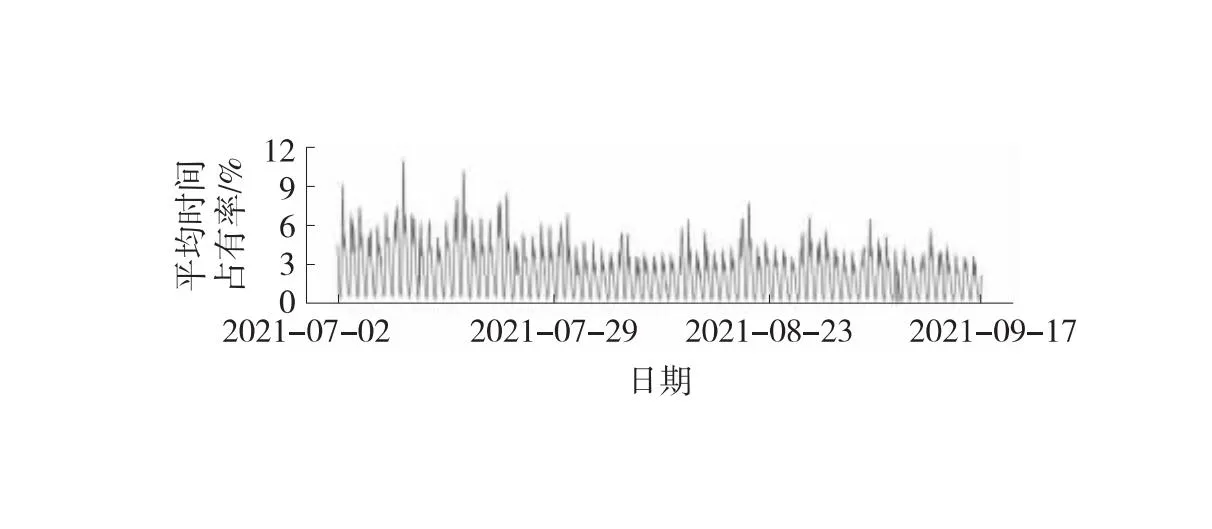
(c) 平均时间占有率
3.2 训练SA-RF修复模型
1) 参数寻优
在模型训练阶段应用MSE误差函数计算模型损失值,可有效评估训练模型准确性。以SA算法对RF模型参数寻优,调整主要参数和搜索空间,如表3所示。在SA算法中,以RF预测值与真实值的MSE作为目标函数,衡量在每种参数组合下的目标函数值,全局搜索最小MSE的参数组合。其中设置初始温度100 ℃,退火速率0.99,结束低温0.01 ℃。
2) 训练单变量或多变量修复模型
根据单变量修复模型数据集,设定时间窗口k=24,即待修复数据前24个时刻交通流数据作为特征训练向量,分别形成3条单变量训练数据集,每个数据集包含1 521条训练特征向量。分别对交通流参数Q、V、Oc训练SA-RF单变量修复模型,并寻找最优参数。经过训练后,结果如图3所示。图3中,从左到右分别为Q、V、Oc序列的SA-RF模型迭代误差曲线,最终趋向与x轴平行的曲线为SA-RF最优迭代误差曲线。
同理,针对多变量修复模型,设置空间特征维度k=2,构建对应训练数据集,分别对交通流参数(Q,V)-Oc、(Q,Oc)-V、(Oc,V)-Q训练SA-RF多变量修复模型,并寻找最优参数,单变量和多变量的最优参数如表3所示。
3.3 SA-RF综合修复模型
由于修复模型存在前置限制条件,单变量修复模型要求完整时间序列的交通流数据,可用于修复单变量和多变量数据缺失模式;多变量修复模型要求同一时间维度的其他交通流特征未缺失,可用于修复单变量缺失模型。公路隧道交通流缺失数据具有随机性、复杂性和时空性,缺失模型存在单变量缺失和多变量缺失共存的情况,从表3中可知,多变量修复效果远高于单变量修复效果。因此,以多变量修复模型为主,单变量修复为辅,建立基于SA-RF的综合修复模型,全方位、高精度修复公路隧道缺失数据。
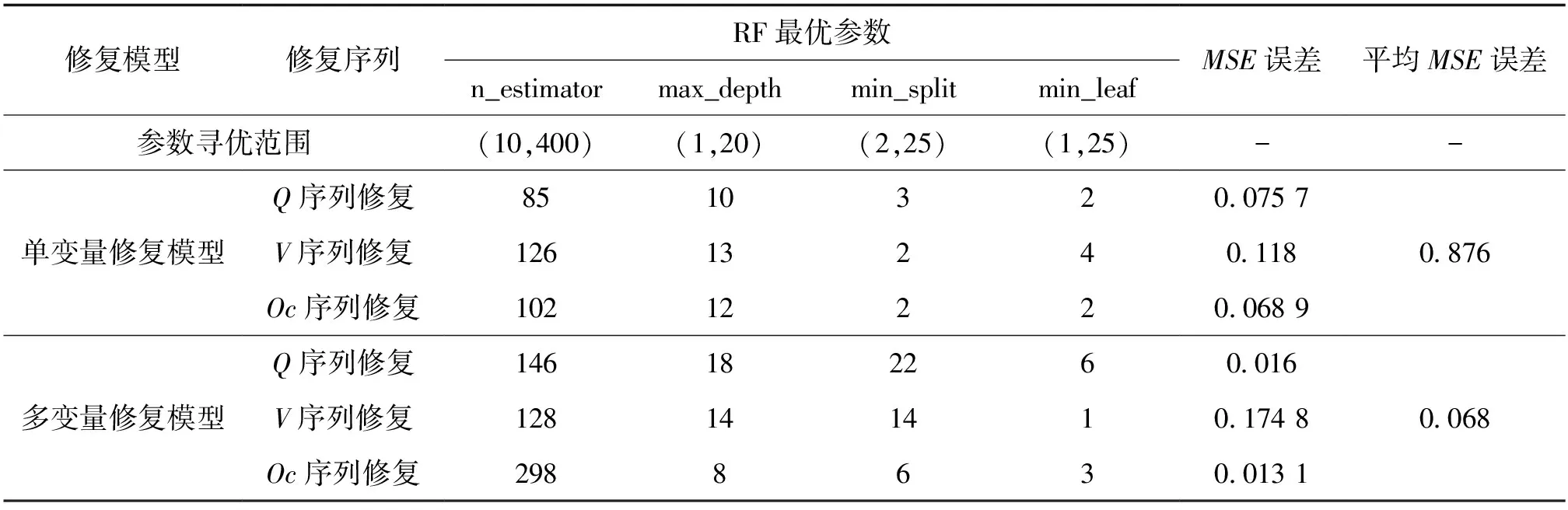
表3 SA-RF修复模型最优参数与误差
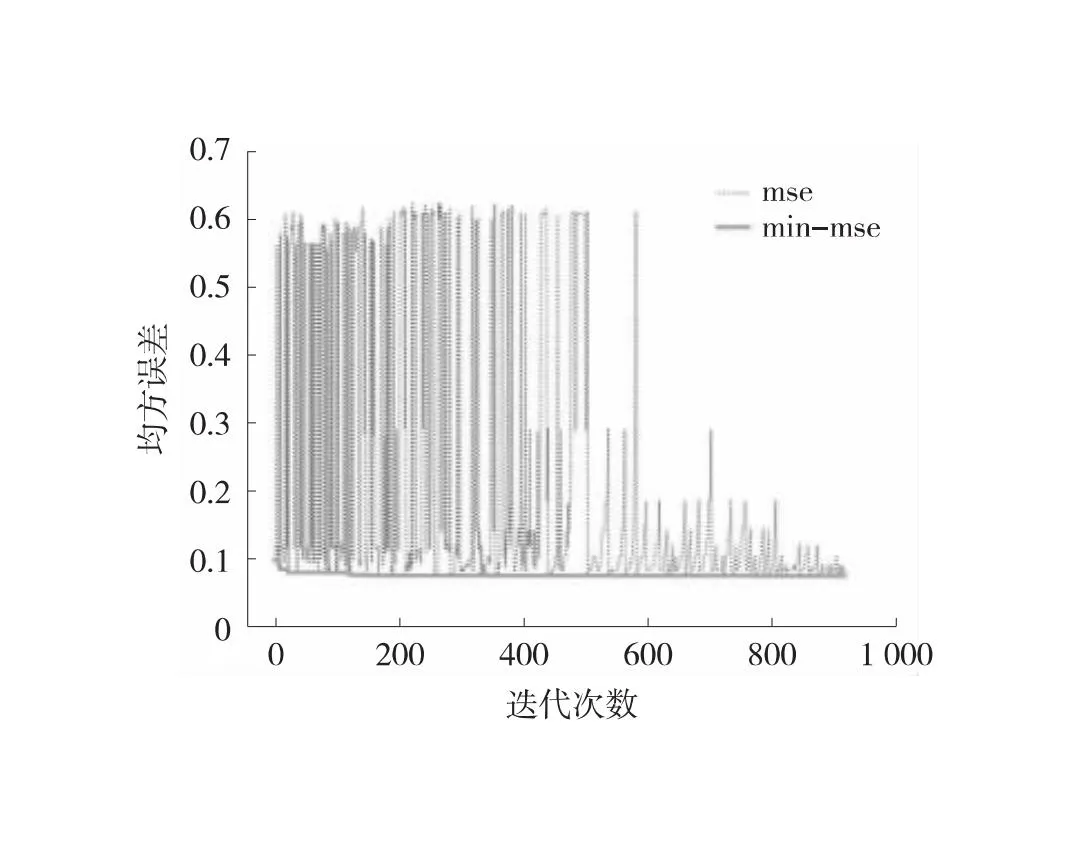
(a) Q序列

(b) V序列
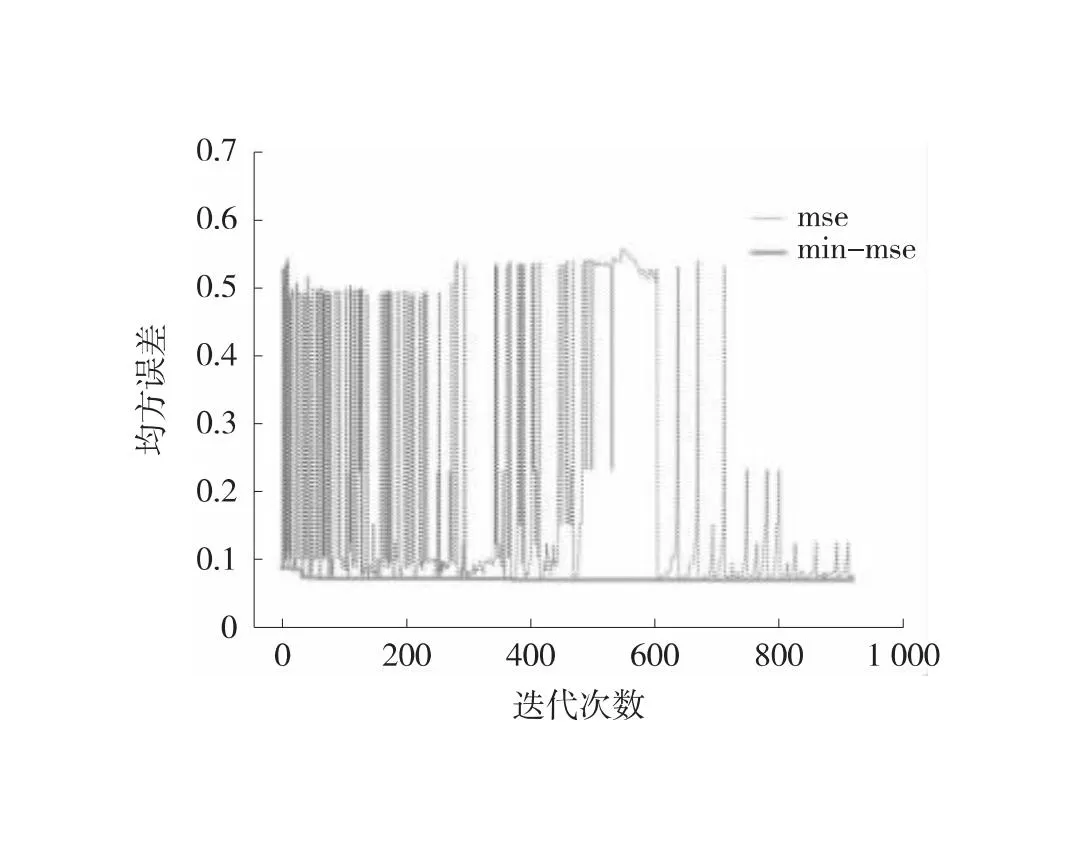
(c) Oc序列
在交通流测试集上分别构建3%、5%、10%和15%缺失比例的随机缺失数据,利用SA-RF模型分别对4种缺失率下的测试集进行修复,其修复效果如图4所示。图4中,曲线表示缺失交通流数据和修复交通流数据曲线。从图4中可见,SA-RF模型预测修复曲线贴近于原始交通流曲线,大部分修复值点靠近真实值点,甚至部分点位重合,修复效果较好。

(a) 交通量(3%缺失率)
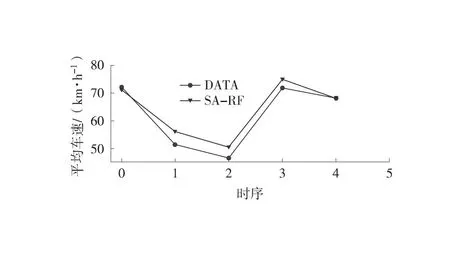
(b) 平均车速(3%缺失率)
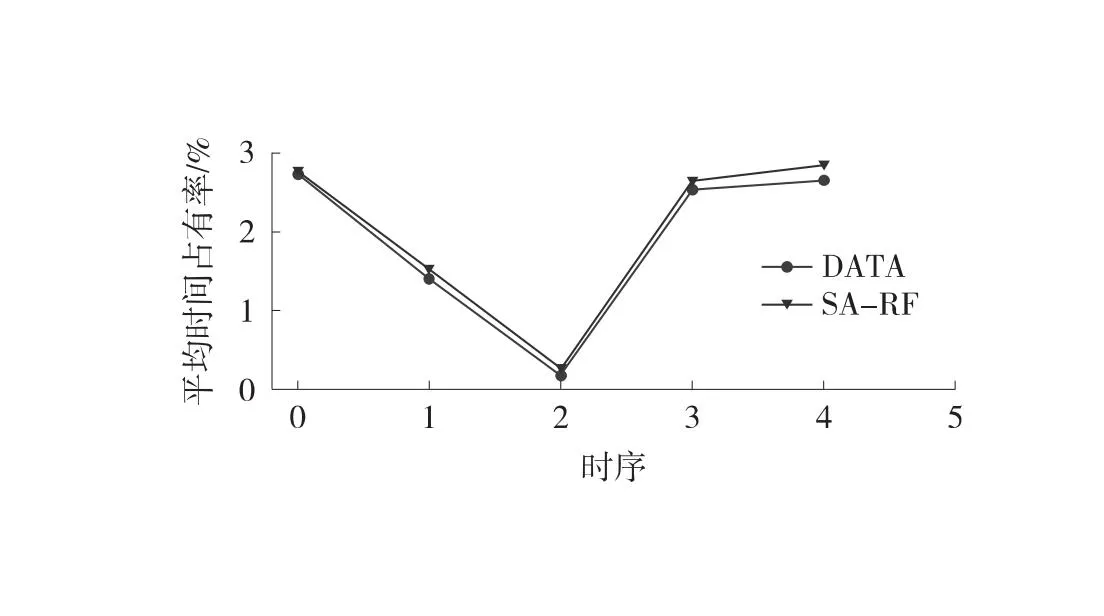
(c) 平均时间占有率(3%缺失率)
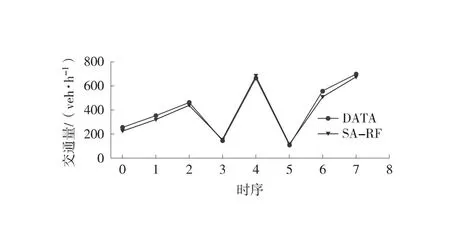
(d) 交通量(5%缺失率)
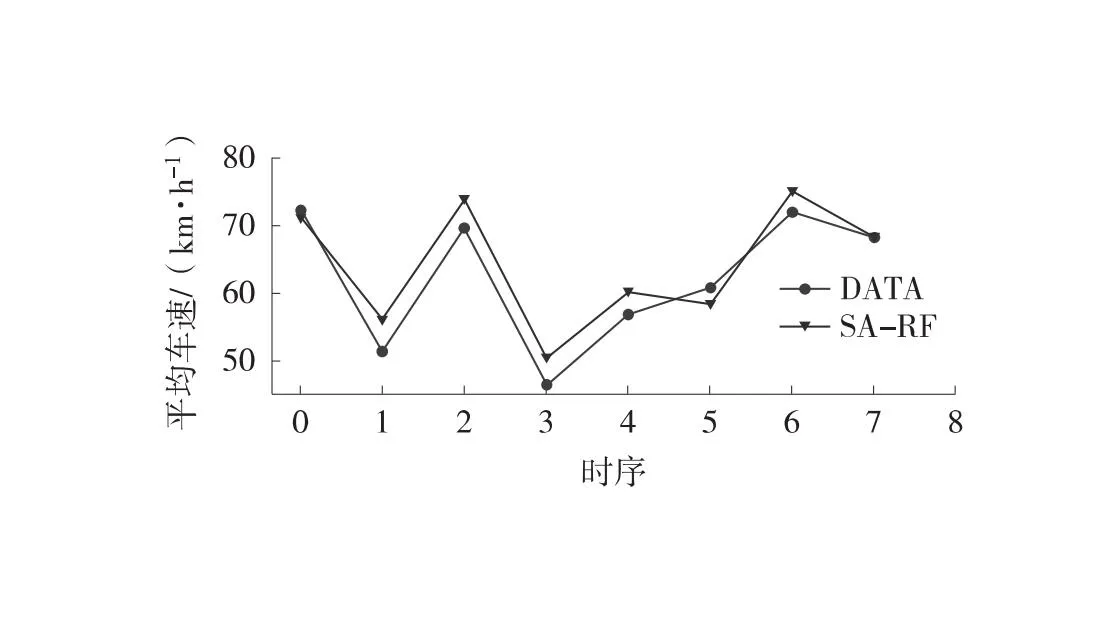
(e) 平均车速(5%缺失率)
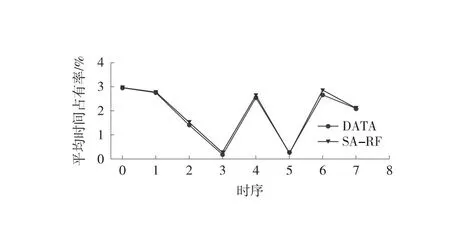
(f) 平均时间占有率(5%缺失率)
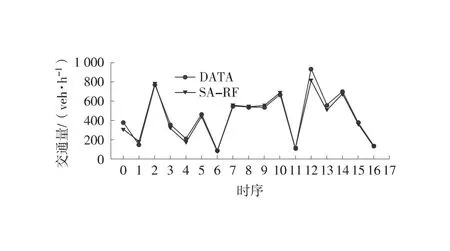
(g) 交通量(10%缺失率)

(h) 平均车速(10%缺失率)
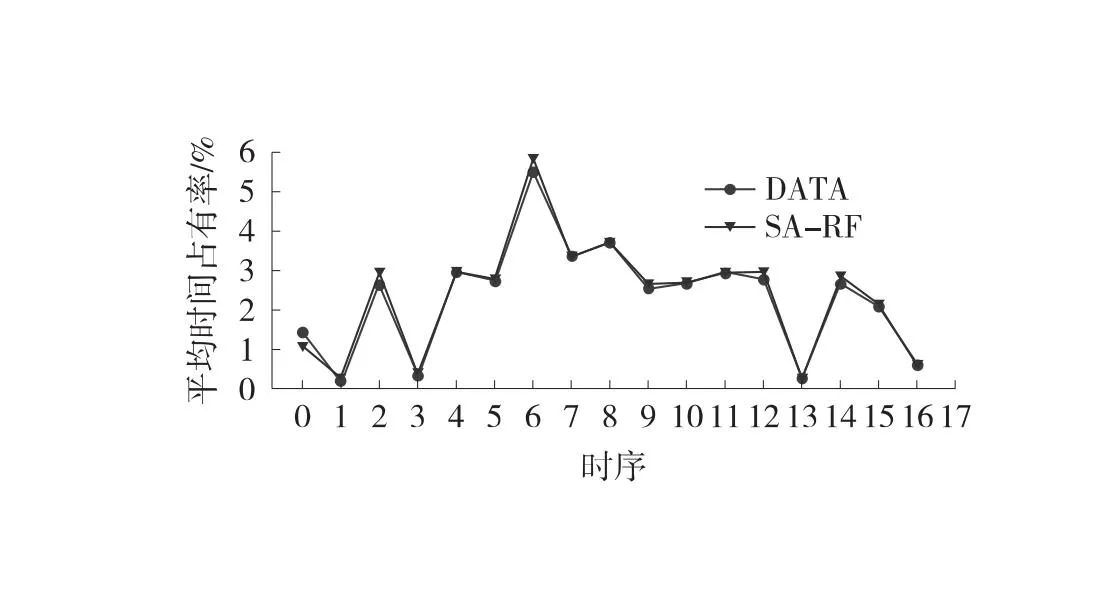
(i) 平均时间占有率(10%缺失率)

(j) 交通量(15%缺失率)
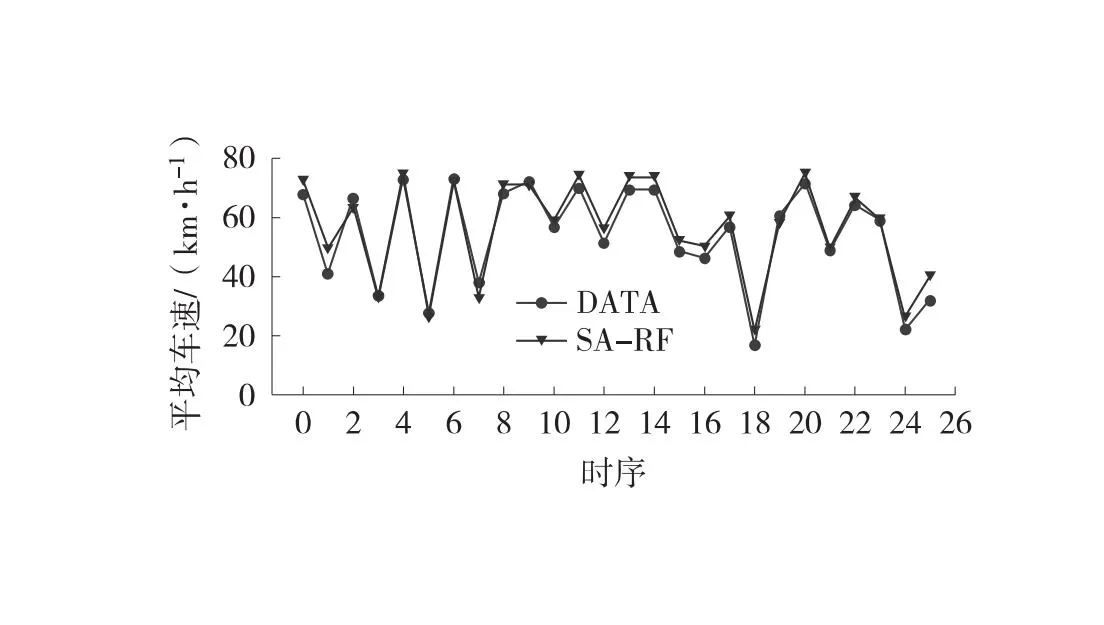
(k) 平均车速(15%缺失率)
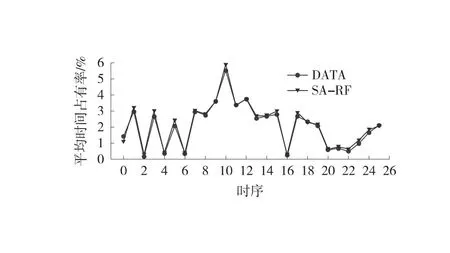
(l) 平均时间占有率(15%缺失率)
3.4 修复模型对比分析
为验证基于SA-RF的综合修复模型的准确率,选取RF、LSTM、均值插补修复模型对比分析,通过相同的训练数据集进行训练,按照随机缺失率3%、5%、10%、15%划分测试集,并预测修复缺失值。为综合比较交通流修复效果,避免MSE会惩罚大偏差,以MAPE衡量交通流修复效果,结果如表4、图5所示。
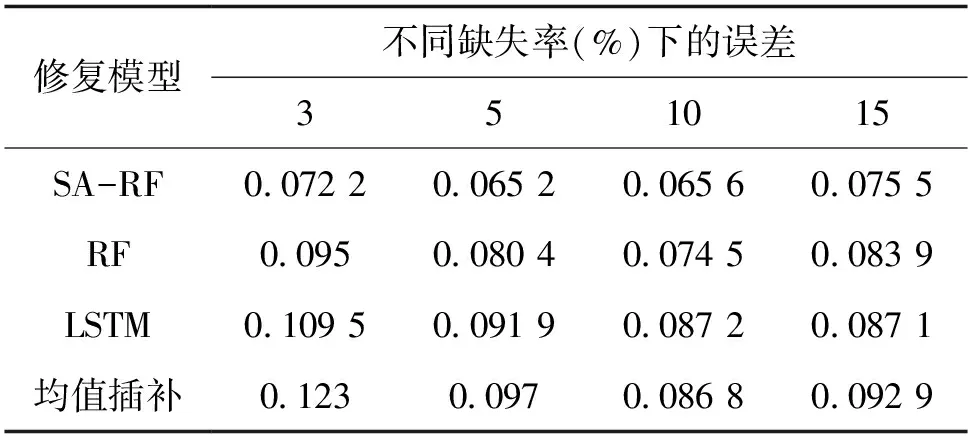
表4 不同缺失率、修复模型的误差

图5 不同修复方法的MAPE对比
MAPE反映修复数据偏离真实值的相对程度,MAPE值越小则修复值与真实值的相对偏差越小,修复精度越高。从图5中可知,经SA模型调参优化,RF在不同缺失率下修复精度均得到提升,在3%缺失率时,SA-RF模型较未调参RF模型的MAPE降低24%。4种缺失率下使用SA-RF修复模型的MAPE值均低于RF、LSTM和均值插补修复模型,SA-RF修复曲线更贴近原始数据曲线。其中,在3%缺失率下,SA-RF修复模型相较RF、LSTM和均值插补办法,修复效果分别提升了24%、34.06%和41.3%。对比不同缺失率下的SA-RF修复模型效果,结果表明,在5%缺失率时修复效果最好,相较15%缺失率,修复效果提升了13.64%,修复效果显著。
4 结论
1) 基于模拟退火算法优化的随机森林预测模型(SA-RF)能很好实现对低缺失率(5%)的交通流数据修复。
2) SA-RF模型预测效果优于传统RF模型,在一定程度上通过SA模型进行参数寻优,可降低RF模型的修复误差,提升模型预测准确性。
3) 根据交通数据的时间相关性和空间相关性分别建立单变量和多变量修复方式,构建相应训练数据集、训练和预测模型,将2种修复方式相结合建立SA-RF综合修复模型。该模型可实现高精度和高鲁棒性修补交通流数据。
4) 在交通流缺失率为3%、5%、10%和15%时,对比SA-RF修复模型与其他模型的修复效果,结果表明,SA-RF在不同缺失率下均可高精度修复交通流缺失数据,且修复误差指标MAPE均低于同等缺失率的RF、LSTM、均值插补修复模型。
