超临界CO2再热再压缩布雷顿循环火力发电系统分析

2024-01-10刘国浩余廷芳

南昌大学学报（工科版） 2023年4期

刘国浩,余廷芳

(南昌大学先进制造学院,江西南昌 330031)

能源问题是当前世界关注的焦点问题,超临界CO2(supercritical carbon dioxide,SCO2)布雷顿循环因其诸多优点,具有巨大的发展前景[1],在太阳能发电[2]、核能发电[3]、余热发电[4]等领域受到国内外学者的广泛关注。

SCO2布雷顿循环由Sulzer在20世纪40年代最先提出,20世纪60年代Angelino[5]和Feher[6]开始关于SCO2发电技术的研究。直到2004年Dostal[7]提出再压缩布雷顿循环,并且与传统的朗肯循环相比,SCO2布雷顿循环不仅能在较低的涡轮进口温度(550 ℃)下达到较高的热效率(45.3%),而且具有体积小,结构紧凑,可以降低发电厂的成本等优势,SCO2发电技术才被学者所重视。目前,在简单布雷顿循环的基础上,SCO2循环已经演变出42种独立循环模式和38种联合循环模式[8],其中代表性的有:1)日本东京工业大学提出的用于气冷快堆和热反应堆的部分冷却循环,可以减少热量的损失,在650 ℃的中等温度条件下达到较高的热效率[9];2)美国爱达荷国家实验室和麻省理工学院联合开发的用于铅-铋合金冷却反应堆的SCO2循环,增加了中间换热器,有利于热量交换[10]。郑开云对SCO2循环的冷端温度进行优化[11],同时研究发现,相比于再压缩循环,部分冷却循环与锅炉集成时能有效解决工质进入锅炉温度高,吸热温度区间窄,流量大的问题[12]。周昊等[13]建立了SCO2布雷顿再压缩循环塔式太阳能光热系统,并对影响系统性能的关键参数进行优化。张一帆等[14]利用Fortran语言建立SCO2布雷顿循环火力发电系统的计算模型,并对影响系统性能的关键参数进行了分析。

可以看出,国内外对SCO2布雷顿循环的研究主要集中在对再压缩布雷顿循环的热力分析,对含有再热的布雷顿循环研究较少。而与无再热的布雷顿循环相比,有再热的布雷顿循环的热效率普遍高出1～2个百分点,再热温度升高可提高循环效率,但再热温度的提高受到透平和入口管材料的限制,通常会选择高压透平的入口温度为再热温度[15]。此外,以往学者的研究大多是针对太阳能、核能、余热利用等领域,而对火电系统的SCO2布雷顿循环研究鲜有报道。

火用分析方法以热力学第二定律为分析基础,相比于热效率分析法,能更全面揭示能量损失的环节及其损失的原因,为提高能量利用率指明方向。因而本文建立了SCO2一次再热再压缩布雷顿循环火力发电系统性能计算及火用分析模型,深入分析了系统的火用损分布及各关键参数对循环性能的影响,指出了系统的火用损关键环节,为系统的参数优化及性能改进提供参考。

1 SCO2一次再热再压缩布雷顿循环

SCO2一次再热再压缩布雷顿循环示意图如图1所示。循环流程主要为:从低温回热器(low temperuture reheater,LTR)中定压放热(10→11)出来的工质进行分流,一部分工质直接进入再压缩机压缩(11→12),另一部分工质经过预冷器冷却(11→1),状态参数略高于临界状态(31.1 ℃,7.38 MPa),然后进入主压缩机进行压缩(1→2),后进入低温回热器吸热(2→3),再与直接被再压缩机压缩的工质混合进入到高温回热器(high temperuture reheater,HTR)中加热(4→5),之后工质在锅炉中吸热(5→6),一次工质进入到高压膨胀机中做功(6→7),做功完成的二次工质再次进入到锅炉中进行加热(7→8)温度升高到高压膨胀机的进口温度,随后进入低压透平中做功(8→9)并带动发电机工作,做功完成的乏汽回到高温回热器中放热(9→10),再进入低温回热器中进行热交换(10→11),最终完成闭式布雷顿循环。

2 数学模型

2.1 模型的建立

为了简化热力学计算模型,作如下假设:1)系统处于稳定流动状态;2)循环过程不考虑压降;3)忽略工质的动能和位能;4)系统各部件绝热。循环的数学模型如式(1)～式(15)所示。

吸热量

Q=qm[(h6-h5)+(h8-h7)]

(1)

输入火用

Ein=Q/ηr

(2)

透平输出功

Wt=qm[(h6-h7)+(h8-h9)]

(3)

主压缩机耗功

Wc1=xqm[(h2-h1)]

(4)

再压缩机耗功

Wc2=(1-x)qm[(h12-h11)]

(5)

各状态点的火用

ei=(hi-h0)-T0(si-s0)

(6)

锅炉火用损率

Ir={qm[(e5-e6)+(e7-e8)]+Ein}/Ein

(7)

透平火用损率

It={qm[(e6-e7)+(e8-e9)]-Wt}/Ein

(8)

高温回热器火用损率

IHTR=qm[(e9-e10)-(e5-e4)]/Ein

(9)

低温回热器火用损率

ILTR={qm[(e10-e11)-xqm(e3-e2)]}/Ein

(10)

主压缩机火用损率

Ic1=[Wc1-xqm(e2-e1)]/Ein

(11)

再压缩机火用损率

Ic2=[Wc2-(1-x)qm(e12-e11)]/Ein

(12)

预冷器火用损率

Ip=[xqm(e11-e1)]/Ein

(13)

发电机火用损率

Ie=(Wt-Wc1-Wc2)(1-ηe)/Ein

(14)

系统火用效率

η=(Wt-Wc1-Wc2)ηe/Ein

(15)

式(1)～式(15)中:qm为工质的质量流量,单位为kg·s-1;x为分流比,流经主压缩机的质量流量与总质量流量的比值;Q为热量,单位为kJ·s-1;Ein为系统输入火用,单位为kJ·s-1;h为比焓,单位为kJ·kg-1;s为比熵,单位为kJ· (kg·K)-1;e为比火用,单位为kJ·kg-1;T0为环境温度,单位为K;h0和s0为环境的比焓和比熵;η为效率;I为火用损率;W为功率,单位为kW。下角标,i表示各状态点,t表示透平c1表示主压缩机,c2表示再压缩机,r表示锅炉,p表示预冷器,e表示发电机,HTR表示高温回热器,LTR表示低温回热器。SCO2各点的状态参数利用MATLAB调用REFPROP数据库获得。

2.2 计算模型的验证

为了验证计算模型,选用文献[16]中再热模型的实验数据进行验证。参照文献中系统部件的参数设置,将压缩机和透平的效率设为0.92和0.94,发电机效率设为0.95,质量流量设为1 395 kg·s-1,分流比设为0.73,夹点温差设为5 ℃。计算结果与文献[16]中的实验数据对比如表1和表2所示。

3 计算结果及分析

3.1 系统设计参数

系统对应的主要基准参数如表3所示。

表3 系统主要基准参数

3.2 分流比对火用效率的影响

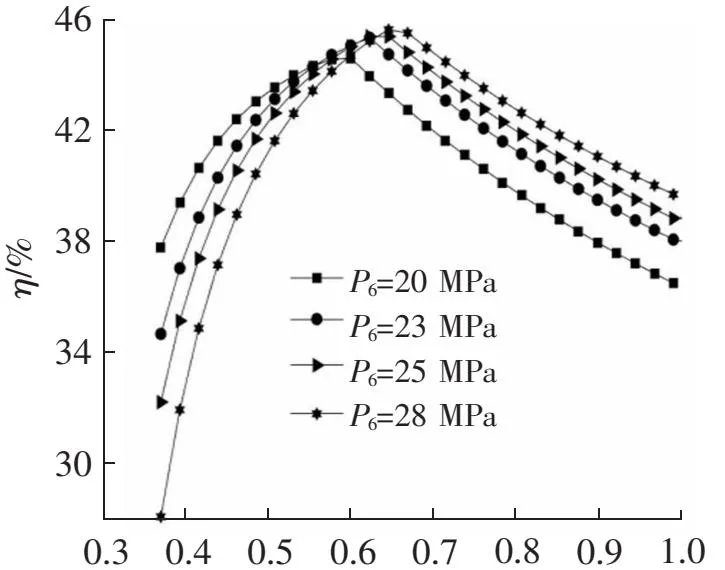
采用分流再压缩,一方面可以减少进入预冷器工质的质量流量,减少放热量,另一方面可平衡低温回热器两侧的温升,提高低温回热器的回热度,故分流比是影响循环性能的关键参数。图2是分流比对系统火用效率的影响,随着分流比的增大火用效率先增加后减少,存在一个最佳分流比,此时循环的火用效率达到最大值。这是因为回热器的回热度对循环的火用效率影响较大,当分流比取最佳值时,回热器的回热度α最高。回热度α的计算式如下:

(16)

式中:Thin为回热器高温侧入口温度,单位为K;Thout为回热器高温侧出口温度,单位为K;Tcin为回热器低温侧入口温度,单位为K。

以图2中透平入口压力P6=20 MPa为例,回热器的回热度随分流比的变化如表4所示。从表4的数据可以看出,当分流比小于0.599时,随着分流比的增大高温回热器和低温回热的回热度都增加,因此循环的火用效率增加。当分流比大于0.599时,随着分流比的增加,低温回热器的回热度(αLTR)从0.925增加到0.955,增幅为3.24%。高温回热器的回热度(αHTR)从0.976减少至0.785,减幅为19.57%。高温回热器回热度的减幅大于低温回热器回热度的增幅,因此系统的火用效率下降。分流比0.599为该组工况下的最佳分流比。

表4 不同分流比下回热器的回热度及火用效率

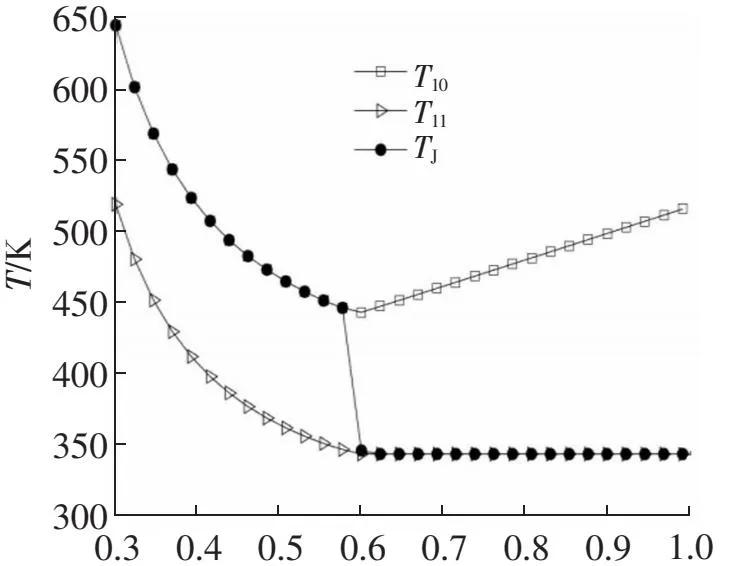
以往的有关研究[3,17-18]认为低温回热器的内部出现夹点会使其回热度降低,影响循环性能,因此相关学者的研究都是基于夹点位于低温回热器高温侧的出口进行的。图3(P6=20 MPa)为低温回热器的夹点位置随分流比的变化情况,图中TJ表示夹点。回热器的夹点先位于低温回热器高温侧的进口,当分流比为0.599～0.622之间时,夹点位于低温回热器的内部,最后夹点位于低温回热高温侧的出口。从本文结论来看,夹点位于低温回热器的内部时循环的火用效率最高,因此要使循环达到真正的最优工况,应综合考虑高温回热器和低温回热器回热度对循环性能的影响。

由图2可知,不同透平入口压力下系统的最佳分流比也不同。透平入口压力为20、23、25、28 MPa时,最佳分流比分别为0.599、0.615、0.622、0.645,透平入口压力越高,最佳分流比越大。这主要是因为在不同的压力下,二氧化碳的物性不同,当回器的回热度最大时,低温回热器冷、热流体的比例不同,即最佳分流比不同。

3.3 分流比对各部件火用损分布的影响

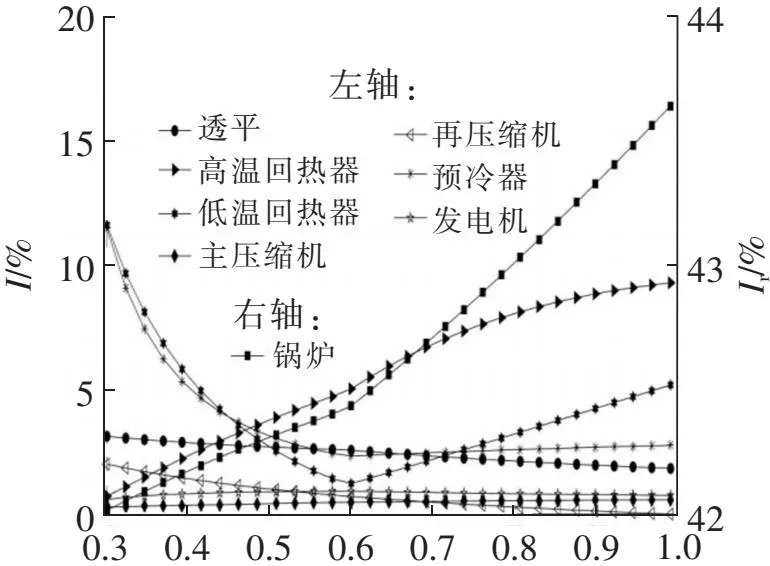
表5为不同分流比下部件火用损分布及火用效率,图4为系统各部件的火用损率随分流比的变化。可见,锅炉、回热器、预冷器的火用损率受分流比的影响最大。随着分流比的增加锅炉的火用损率显著增加,这是因为分流比的增加使工质进入预冷器的质量流量增加,系统放热量增多,一次工质进入锅炉中的吸热温度降低,从而导致工质与热源间的温差加大。另外,一次工质温度下降意味其在锅炉中的吸热量更多,燃煤的质量流量也随之增加,这就导致了燃料燃烧时的不可逆火用损失加大。从表5及图4还可以看出,锅炉的火用损占据了整个系统火用损的绝大部分,这也是因为燃烧是典型的不可逆反应,燃烧过程中会有大量的火用损失。对于回热器,高温回热器的火用损率也是一直增加,这是因为高温回热器内工质间的温差不断增大,使其火用损增加。而低温回热器内夹点随着分流比的增加从高温侧的进口向出口移动,内部温差先减少后增加,低温回热器的火用损率也呈现相同的变化趋势。对于预冷器,工质与冷源之间的温差先减少后不变,但预冷器的质量流量一直增加,因此火用损系数先减少后缓慢增加。

表5 不同分流比下的火用损分布和火用效率

表6 不同主压缩机入口温度下回热器回热度和火用效率

分流比对透平、压缩机和发电机火用损率的影响并不显著。分流比增加,系统输入火用增加,而透平做功与分流比无关,因此透平的火用损率减少。对于压缩机,随着分流比的变化,工质进入主压缩机和再压缩机的质量流量不同,其火用损率也呈现出不同的变化趋势。

3.4 再热参数对火用效率的影响

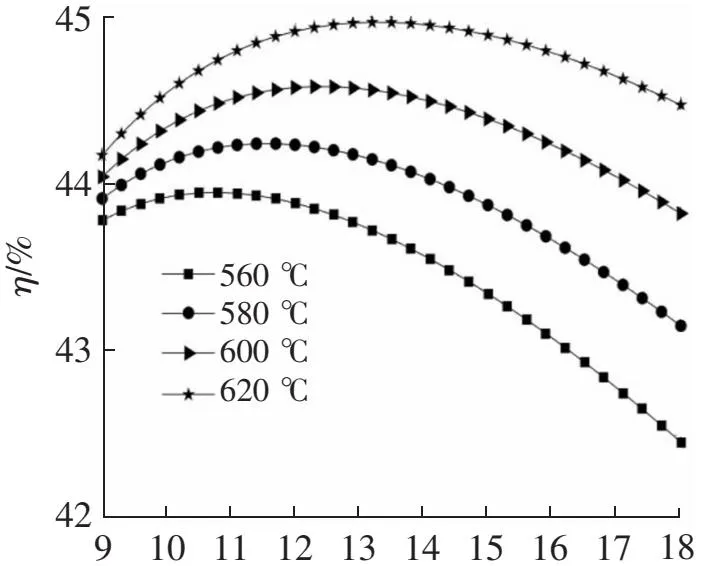
含有再热的布雷顿循环,再热参数会对循环性能产生直接的影响。图5给出了不同再热温度下,火用效率随再热压力Pr的变化规律。数值模拟结果表明,再热压力增加,系统的火用效率先增加后减少,存在一个最佳的再热压力。再热温度为560、580、600、620 ℃时,对应的最佳再热压力分别为10.8、11.7、12.3、13.5 MPa,随着再热温度的升高,最佳再热压力也随之升高。这是因为再热温度升高,二次工质的品质提高,做功能力加强。此时,增加再热压力,适当的减少高压透平压降在透平总压降的比例,有助于提高系统的火用效率,即在系统最低压力不变时,适当的提高再热压力可以提高系统的火用效率。

Pr/MPa

3.5 主压缩机出口压力对火用效率的影响

主压缩机的出口压力是循环过程中的最高压力,对系统火用效率会产生重要的影响。对含分流再压缩的布雷顿循环而言,系统的火用效率并不会像简单布雷顿循环那样随着循环最高压力的提高而一直上升。这是因为循环的最高压力和分流比会互相约束,只有两者都取合适的值时,系统的火用效率才能达到最高。

图6给出了不同分流比下,主压缩机出口压力P2对系统火用效率的影响。由图6可知,当分流比较大时(分流比等于0.699或0.799),系统的火用效率受主压缩机出口压力的影响较大,火用效率随出口压力的增加而增大,这与简单布雷顿循环的变化规律一致。当分流比变小时,主压缩机出口压力对系统火用效率的影响也随之减少,出口压力变大,火用效率并不是单调递增,而是先增加后减少。这是因为:以分流比等于0.599为例,主压缩机出口压力小于20 MPa时,主压缩机出口压力提高,工质参数提升,系统效率也随之升高,且此时的分流比接近最佳分流比(循环最高压力20 MPa,最佳分流比为0.599);主压缩机出口压力继续升高,最佳分流比增大,诺分流比继续保持为0.599,会使系统的火用效率降低,且降低的幅度大于工质参数提升所带来的系统火用效率提升的幅度。因此,当主压缩机出口压力继续升高时,会使系统的火用效率下降。

P2/MPa

3.6 主压缩机入口温度对火用效率的影响

为了确保工质在整个循环过程中都处于超临界状态,本文仅讨论主压缩机入口温度t1大于等于32 ℃的工况。图7为不同分流比下,主压缩机入口温度t1对火用效率的影响。从图7可以看出,当分流比等于0.599时,系统的火用效率随主压缩机入口温度的升高而下降。这是因为当分流比等于最佳分流比(0.599)时,回热器的回热度最高,升高主压缩机入口温度,会使回热器冷侧工质温度升高,工质的物性也随之改变,回热器的回热度下降,系统的火用效率下降。当分流比不等于最佳分流比时,系统的火用效率随主压缩机入口温度的升高,先上升后下降。

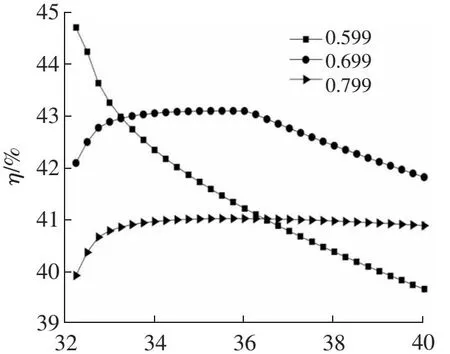
t1/℃

表7给出了分流比为0.699时,不同主压缩机入口温度对应的回热器的回热度和火用效率。当t1从32 ℃升高至36 ℃时,高温回热器回热度上升,低温回热器回热度下降,回热器的总回热度上升,此时系统的火用效率随t1的升高而上升。当t1从36 ℃升高至40 ℃时,高温回热器的回热度基本保持不变,低温回热器的回热度下降,回热器的总回热度下降,此时系统的火用效率随t1的上升而下降。