一种工业补燃燃烧器导流设计与强度分析

占双剑,孙仁权,黄晓明,陈滢

(1.苏州先机动力科技有限公司,江苏 苏州 215123;2.安德森热能科技(苏州)有限责任公司,江苏 苏州 215123;3.华中科技大学能源与动力工程学院,湖北 武汉 430074)

燃气-蒸汽联合循环电站是目前国际上发展最快的发电形式之一,具有发电效率高、建设周期短、操作方便、调峰能力强等优点。当燃气轮机的排气温度不能满足产生数量足够多和温度足够高的蒸汽时,业界基本采用安装余热锅炉(heat recovery steam generator,HRSG)的办法。作为常规的燃机余热锅炉,燃机的排气参数决定了余热锅炉的蒸汽产出。而当对余热锅炉的蒸汽参数要求更高时,比如蒸汽产量要求增加,或蒸汽温度要求较高,这就要考虑到增加补燃来实现,在具有补燃型余热锅炉的联合循环系统中,燃烧器用于补燃,以增加燃机排气所含的热量,提高下游HRSG的出力。其补燃设备-燃烧器系统的正确设计可以提高联合循环电站的变工况特性,同时过渡烟道的设计及其中部件在余热锅炉中的布置对余热锅炉的安全运行起到了重要的作用,这也将直接影响余热锅炉的安全性和使用寿命[1]。

目前,常规烟道的设计只需要考虑燃机出口到受热面模块进口这段烟道的流动均匀性,而补燃式烟道,要考虑补燃器前后的流场均匀。为提高传热效率,在过渡烟道入口处增设导流板用于引导烟气流场,保证气流在较短的扩散烟道中快速扩散均匀[2],再经由燃烧器提高补燃温度,补燃后的混合烟气抵达一级受热面时流场须均匀稳定,以保证燃烧器后的受热面的传热效果。

在传统的设计过程中,无论是针对风道结构的改善还是加装的导流结构合理性验证,只能通过反复的实验进行摸索,整个过程会消耗极大的人力、物力以及时间,联合循环系统的落地过程也会因此进展十分缓慢。随着计算力学技术的日益发展,基于仿真的分析手段在工程应用中不断取得成功,国内外科研单位和工程师开始逐渐将数值模拟技术应用于余热锅炉领域。如导流板的形状、导流板的位置、燃烧器距受热面的距离等设计与优化,都可以采用数值计算模拟或流体模型试验来验证,将燃烧器内气体流场进行可视化,从而直观地反映流体的流动特征,为燃烧器的设计优化提供有力的理论参考依据。

本文基于高精度三维流场仿真结果,设计合理的导流板模型,采用MATLAB程序算法,将温度和压力场映射到导流板结构上,基于HyperMesh-ABAQUS联合仿真先后对其进行常温静力和带温分析用以校核结构强度,研究结构静力可靠性和在高温稳态环境下该结构设计的承载能力和变形合理性,并基于计算结果给出优化意见,从而为研究余热锅炉设计提供参考。

1 模型的建立

在热应力的有限元分析中,对于静态或准静态的问题,可以单纯地考虑温度场对位移场的影响。但在发生热冲击引起高速热应变的情况下,必须考虑变形功对温度场的影响[3-4]。当物体各部分有同样温升时,热膨胀是均匀的,若物体受外界约束,则处于各方向应变都相同的常应变状态,不会产生内部应力。当物体受热,又受到外界约束时,或者内部受热不均匀,则内部会产生内应力。总应变应为热应变和弹性应变之和。1956年,Biot放弃了“体积不变”的假定,考虑变形功的影响导出了带有应变参数的热传导方程[5]。这一方程只适用于一维弹性问题。1977年,竹内洋一郎推导并得到了适用于二维、三维问题的耦合热传导方程[6],但仍然停留在弹性范围内;同时它忽略了温度对材料热物理性能和力学性能的影响。之后的热力耦合分析,或者只在弹性范围内进行分析,或者根本不考虑变形功的影响[7]。

1.1 热力耦合模型

根据胡克定律,得到结构单元的几何方程和用应变表示的热弹性力学物理方程:

(1)

δij=2Gεij+(λ-βT)δij

(2)

由结构单元的平衡方程得到热弹性力学的平衡微分方程:

(3)

式中:fi为坐标轴上单位体积力的分量(i=x,y,z);T为温度;ui为节点位移。

从几何方程、物理方程中消去位移和应变,得到变形协调方程,应用平衡微分方程简化为:

(4)

式中:δi为主应力;

εkk=εxx+εyy+εzz;

总结以上各式得到热-力耦合条件下的表达式为[8-9]:

(5)

式中:M为质量矩阵;C为结构阻尼矩阵;Ct为比热矩阵;K为结构刚度矩阵;Kt为热传导矩阵;F为总等效节点力矩阵;Q为总等效节点热流率向量。

1.2 横向冲击力

烟气通过流道时,导流板在高温热冲击下横向受力。基于动量定理,物体在一个过程中动量的变化量,等于它在这个过程中所受力的冲量:

m·Δv=FΔt

(6)

换算之后,表现为导流板横向受力等于流体质量流量与流度的乘积。累积质量流量为

ml=m/Δt

(7)

联立式(6)、式(7),可求得横向受力为

F=ml·Δv

(8)

1.3 湍流模型

基于物理模型的复杂性,本文采用的是SSTk-ω(shear stress transport)湍流模型。该模型最先由Menter[10-12]提出,其综合了原始k-ω模型[13]在近壁面区域和k-ε模型在远场计算的优点,同时增加了交叉扩散项,在湍流黏性系数的定义中考虑了湍流剪切应力,扩大了模型的应用范围。现有研究表明,SSTk-ω湍流模型相较其他传统湍流模型,具备更好的工程可用性[14-15]。

SSTk-ω湍流模型以湍动能k和其比耗散率ω为求解变量。其中

(9)

湍动能k的输送方程如下所示:

(10)

比耗散率ω的输送方程如下所示:

(11)

式中:右侧前3项分别为生成项、耗散项和扩散项,比耗散率ω方程中的第4项为交叉扩散项;ρ为密度;μ为动力黏度;υt为湍流运动黏度;uj(j=1,2,3)为速度分量;β、σω、σk、σω2,为封闭常数,F1为加权函数。

2 结构设计及材料参数

在烟道折角位置添加导流板来优化此过渡段流场的均匀性,避免气流对下部管道过度冲刷,而上部又没有充足的烟气参与燃烧和换热;同时可以避免气流因为缺乏引导而形成乱流,降低系统效率。导流板的结构设计(图1)是基于过渡段的偏转角度来展开的。烟道中共布置有22块导流板,沿流动纵截面对称布置,每侧11块。所有导流板的折点都与烟道转折点保持一致。

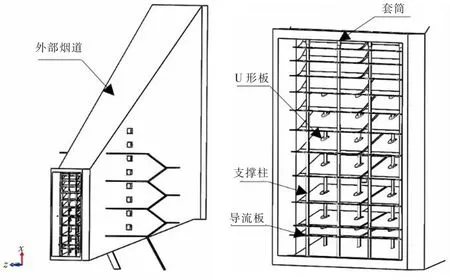
(a) 道结构 (b) 导流板结构

考虑到整体流场的均匀性,首先按照距烟道上端的距离平均排布导流板,计算发现整体的流场均匀导流的效果较不理想,出口截面处的速度分布也不够均匀,在风道末端出现了部分回流,如图2所示。

图2 平均距离的流场分布

为满足过渡烟道流场中流场一致性和流动均匀性的要求,通过调整距离和角度,利用计算流体动力学(computational fluid dynamics,CFD)多次迭代计算,得出了导流板的最佳间隔、最佳的折角角度以及通过计算流速和质量流量后的横向受力,结果如表1所示。按照设计的导流板引流后,到达燃烧器与预定受热面处的流场都呈现较为均匀的状态,这说明导流效果理想,烟气经过导流板之后流动的贴合度很好,没有局部乱流和流动分离,如图3所示。

表1 导流板设计参数

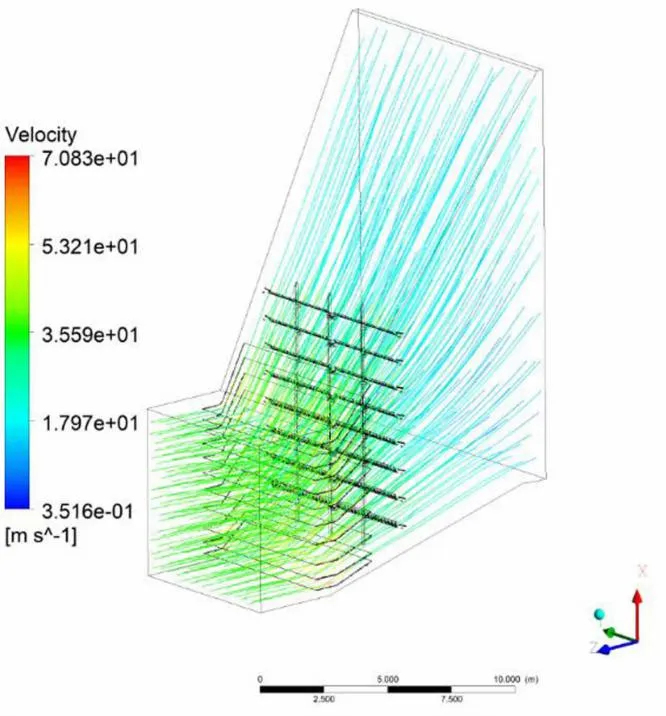
图3 过渡烟道流场分布

过渡烟道入口面的长和高皆为7 380 mm,基于导流板形状使用4根不锈钢空心支撑柱将其贯穿成一列,支撑柱壁厚等相关参数根据设计公式计算得出。考虑到横向受力的影响,为避免圆筒与烟道直接接触产生较大的应力以及摩擦力,在烟道上下相应位置分别设有8个内陷管道凹槽,并且在上端相应位置装有套筒。同时为防止高温热膨胀导致的变形,管径与凹槽皆设有间隙。在每块导流板上下分别加装8块U形夹板来加强导流装置的稳定性。最终设计结构如图1所示,导流板长3 350 mm,宽1 445 mm,厚5 mm,每块导流板分别置于4根支撑柱上,再分别由8块U形夹板固支,组成阵列式导流结构。

对于非定常温度场中的弹性体,温度的变化在弹性体中产生热变形和热应力的同时,也将引起材料性能的改变,并且温度本身的变化也受到弹性体变形及变形速率的影响。因此,热弹性问题中需要考虑热和变形的相互转化关系,相应热传导方程和热弹性运动方程则必须将位移分量和温度变化作为耦合热弹性问题求解。此外,还要考虑物性随温度而变化的影响。文中结构材料皆采用304不锈钢,作为应用最广泛的钢种,其耐热性、耐腐蚀性、强度等特性都较好,具体相关材料参数见表2。

表2 304不锈钢材料强度参数

2.1 有限元分析模型的建立

有限元网格模型(包括节点数据、单元信息、物理特性、材料特性)的建立是用有限元法求解问题的先决条件,在整个求解过程中,它通常具有最大的工作量。值得注意的是,尽管有限元网格自动生成技术有了很大的发展,但是对于大型的复杂结构,仍然存在不少困难。主要表现在2个方面:一是几何特征过多或者过复杂,二是几何特征间尺寸的大小相差悬殊,如一些细节部分,导致网格划分失败或生成网格的质量很差[16]。本文中建立的导流结构的一种实体模型有22块导流板、176块U形板、套筒和支撑柱各8根。要生成其有限元网格,尤其是高质量的结构化网格需要耗费大量时间,对计算机配置要求也比较高。

考虑到只需计算导流板相关区域的应力情况,我们只截取囊括上述导流板结构的部分烟道来构建有限元模型。在此过程中,有限元网格的划分尤为重要,其质量直接关系到计算的精度和速度。本文采取HyperMesh来生成高质量的结构化网格单元。

在进行有限元网格划分时,首先必须确定单元类型。其中导流板与U形夹板可视为薄板结构,采用二维单元划分,其余均使用Sweep方法生成均匀的六面体单元。U形夹板采用刚性连接的方式连接支撑柱,整体网格模型有6 780 001个单元,有限元模型如图4所示。

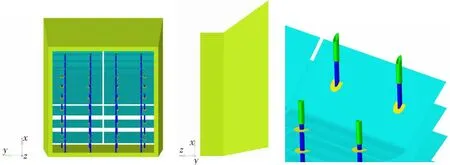
(a) 正视图 (b) 侧视图 (c) 局部结构

2.2 网格收敛性研究

单元类型与单元技术的选择直接影响有限元计算结果的准确性,采用有限元进行压力容器分析设计中,需要得到较准确的应力分布或需得到峰值应力[17]。考虑到网格数量对计算精度的影响,为了保证仿真结果的准确度,需对结构化网格,尤其应力集中区域做网格无关性分析。考虑到导流板形状与导流效果的一致性,通过对最下层板进行试算,对其施加重力和横向受力载荷,从图5观察到导流板与U形夹板接触区域出现应力集中现象,对于该监测区域需要进行网格加密并观察应力收敛情况,如图6所示。

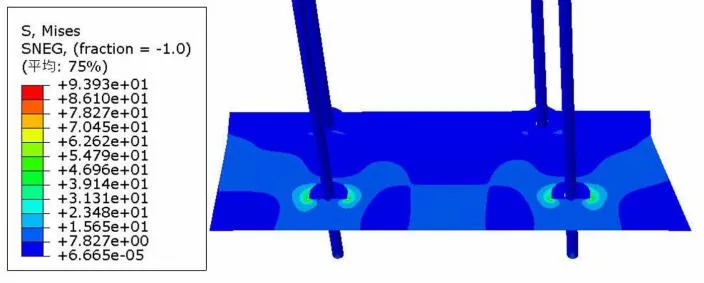
图5 单层板应力云图

图6 应力集中区域

对该区域分别划分5种网格密度进行测试,如表3所示,同时考虑到计算效率,其余区域的网格皆采用10 mm单元尺寸均匀划分。

表3 网格无关性验证

可以看到,随着该区域的网格数量增加,应力水平也随之增大,直到将该层导流板网格增加到106数量级,应力分布趋近于恒定值。综合考虑计算结果精度和计算资源消耗,本文取第四种网格用于接下来的数值模拟。

2.3 常温静力与热力耦合计算

在结构设计之后需要校核装配组件在自重条件下的应力水平,用以分析结构设计的可靠性。同时上述内容表明,导流板系统置于燃机烟道入口处,在工作时受到高温热力的冲击。考虑到温度场计算结果的精度,基于CFD计算出温度场的分布结果,通过MATLAB程序算法将温度场点对点映射到有限元模型上,使输出和输入结果完全匹配,示例如图7所示。

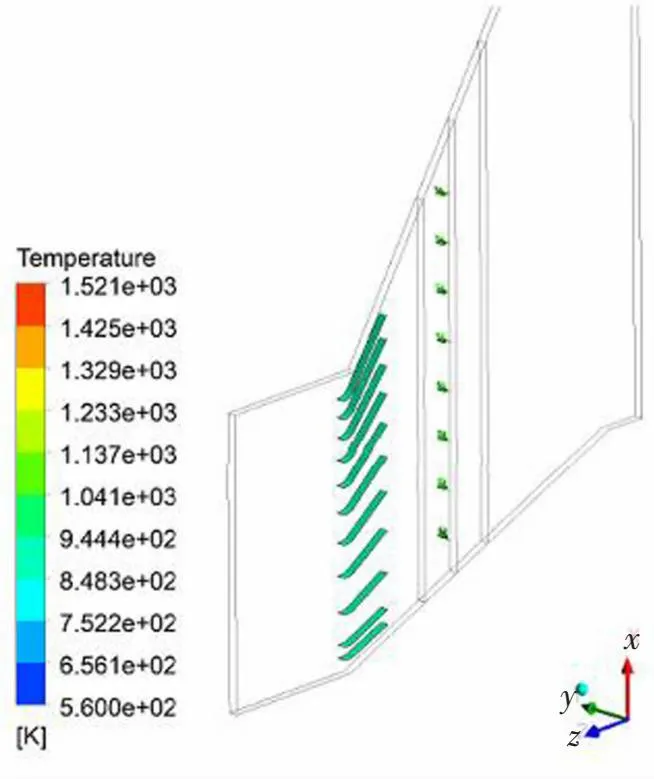
(a) 单列导流板温度场分布

考虑到热求解过程与应力状态无关,应力依赖于热产生,而热并不依赖于位移。将所获取的温度场作为一个预定义场加载到模型当中,再加载横向受力进行顺序耦合热应力分析。

3 结果分析

3.1 自重分析

按照上述的结构模型和描述,计算该结构装配后在自身重力影响下的可靠性。如图8所示,该结构在自重载荷下的位移情况,最大位移8.23 mm发生在自上而下第1层导流板边缘角处,此处是距离支撑板的最远端。

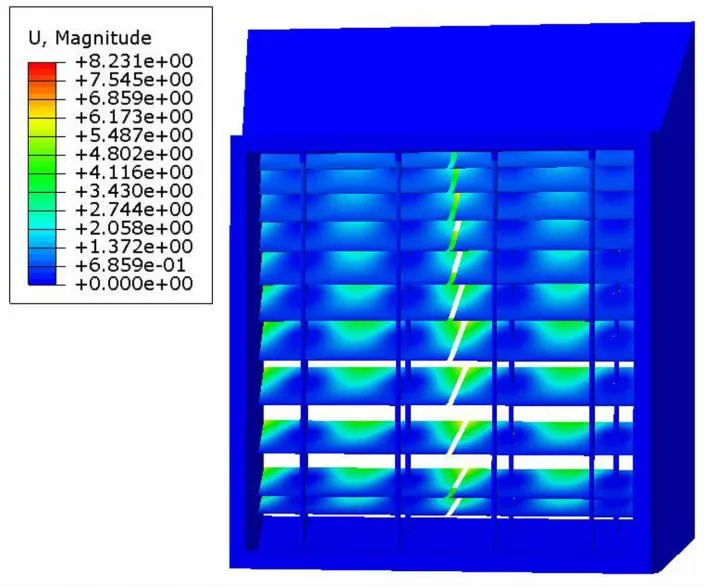
图8 自重分析位移云图

如图9所示,经过计算最大等效应力81.3 MPa发生在由上往下第1层导流板上,其折角角度也最大,等效应力值远小于屈服强度205 MPa,表现为该结构设计在力学性能上的合理性,现有的结构能够正常承载。

图9 自重分析应力云图

3.2 热力分析

在确定结构设计的可靠性之后,对其进行热力耦合分析用以计算真实工况下的应力水平。如图10所示,可以看到最大等效应力245.9 MPa发生在由上往下的第7层导流板上,该位置是所受冲击最大的区域。结果显示应力水平已超出结构材料屈服强度并且出现应力集中的现象,表现为结构无法承载高温的热冲击。

图10 热载荷分析应力云图

经过仿真计算,该结构仅承受静载荷时强度足够,但在高温603.8 ℃环境下,无法承受过大的热冲击,产生较大的翘曲变形。原因不单在于材料性能,也与结构物理性能有关。板材的厚度也会直接影响热变形的程度[18],在工程设计中需着重考虑这些因素。

针对以上计算结果,为避免尖角接触产生的应力集中问题,对导流板进行倒圆角处理,圆角半径取5 mm,同时再进行计算。如图11所示,可以看到应力水平明显下降,最大应力依然发生在由上往下的第7层导流板上,如图12所示,并且在夹板和导流板接触区域的应力趋于平缓,可见在实际工程应用中,受力区域的接触的结构设计还需要多考虑受力状态的影响。

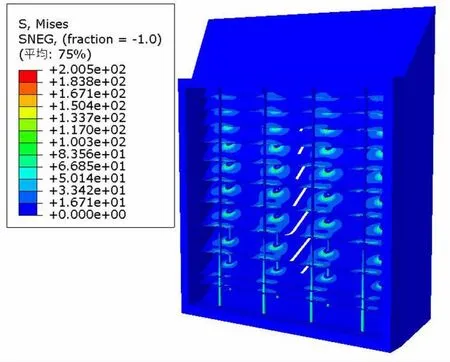
图11 圆角处理后的应力云图

图12 最大应力区域局部

4 结论

1) 通过对流场压差、流速的分析找到导流板最佳的导流角度,根据现有烟道结构设计出合理的导流板模型,并进行常温自重和高温热冲击结构分析。

2) 仿真结果表明,在高温热冲击下导流板出现局部应力集中的现象,高应力区位于U形夹板尖端。可见在工程实施过程中,该种类型的结构,尤其相互接触区域的倒角处理不可忽略。

3) 热冲击载荷下的等效应力稍高于材料屈服强度,原因在于高温下U形板出现翘曲变现,可以考虑适当增加该板的厚度来降低变形程度[19],即可降低整体应力水平。

4) 基于上述结果,可以看到材料在高温载荷下等效应力近乎等同屈服强度,可以考虑更换使用Q345或20MnTiB等耐高温钢材[20]。

5) 本文为基于使用状态的余热锅炉导流板优化设计提供了标准化参考流程。