The Topology Optimization Under the Static Loads

LI Zhibin

(Zhangjiakou Xuanhua Huatai Mining & Metallurgical Machinery Co., Ltd., Zhangjiakou 075100, China)

Abstract：The method of the structural topology optimization is often used to design machine in the early stage of the mechanical design. And one mechanical structure use the topology design to produce a new still and lightweight assembly.

Keywords：mechanical design; FEA; von Mises stress; comparison; topology optimization

1 Introduction

In the early stage of the structural design, the topology optimization is an effective approach, through which a stiff and lightweight machine can be produced. One mechanical structure is used the method of the structural topology optimization to create machine. This paper describes a problem of size optimization, which is about a linear programming problem with stress constraints.

The mechanical structure, described in this paper is part of the working assembly. The topology optimization process given in Figure 1 the process diagram, consists of five steps.

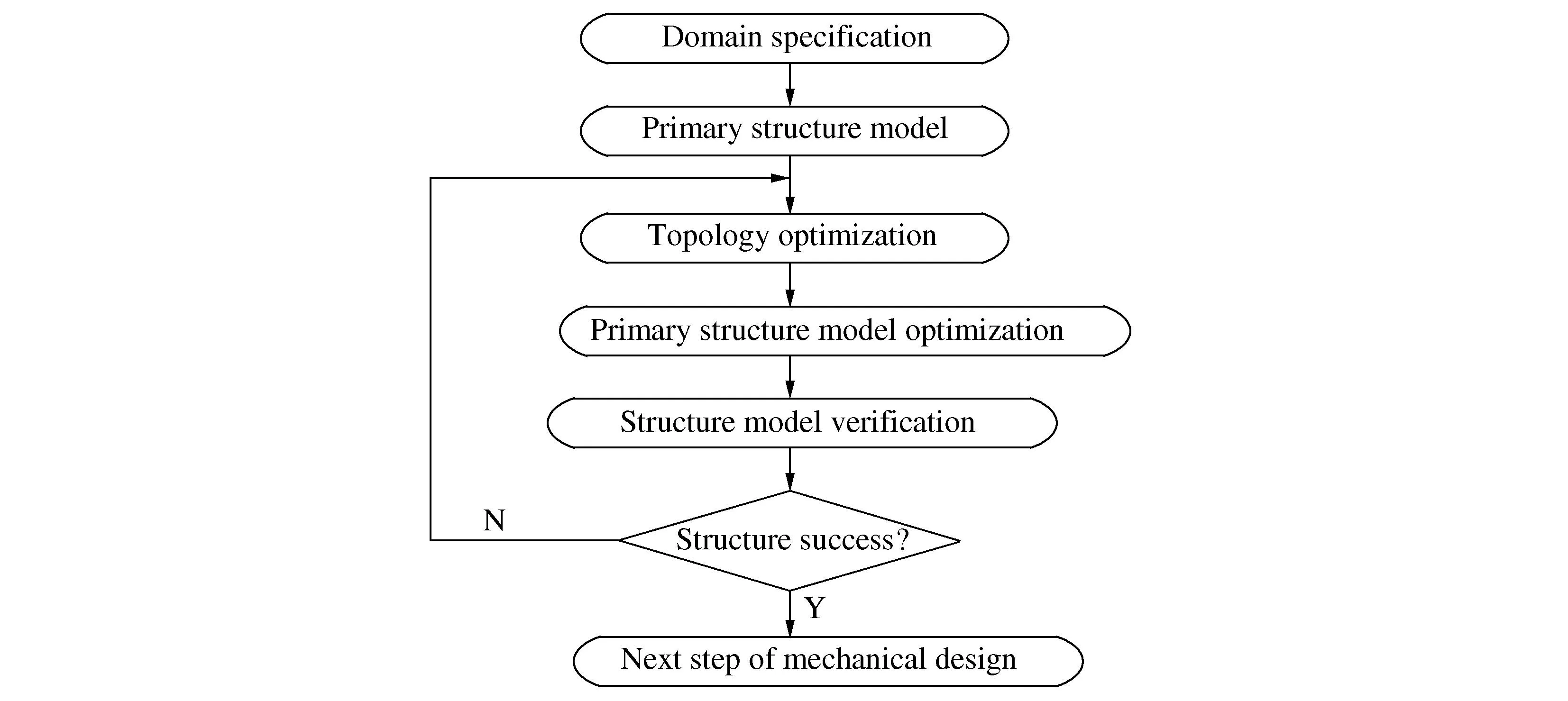
Figure 1 The process diagram

The first step is domain specification. The location of the supports on the working arm has been determined, and the magnitude and direction of the loads[1]are determined by the working state on the step. The material information is known.

The second step is primary structure model, where the initial 3D model is created. The model built is the maximum size allowed according to the working arm and the working condition. The finite element analysis is used for this structure.

The third step is topology optimization. The topology and size optimization is carried out.

The fourth step is primary structure model optimization. According to the result of the topology optimization, the geometry structure model is modified for the initial model on the second step.

The fifth step is structure model verification. The new structure model is analyzed by finite element method. The values of the result are compared to the result of the original structure. If the structure is no success, the third step is carried out again. The type of the response constraint is also mass. While the value of the percent to retain is changed. If the value of the result is little than the original, the next step of mechanical design is carried out, including refined the structure according to the manufacturing situation.

2 The topology optimization of the structure

The initial mode of the mechanical structure has been determined, as shown in the Figure 2. According to the realistic conditions and the materials of other structures of the working arm, the material of the mechanical structure is steel. And the fixed support position of the structure is consistent with the corresponding working assembly. That is the surface of the label A on the Figure 2 the initial model.

Figure 2 The initial model

The location of the oil cylinders mounted on this mechanical structure. So the oil cylinder determines the domain loading. According to the actually working condition, and the pressure of the hydraulic system, the value of loading can be calculated. While The locations of the loading[1]is also known.

The two inner circle on the right side of the Figure 2 the initial model, which is labeled point B, are acted on the force and moment[2]. The force act on the B inner surface in the y direction, the magnitude of which is -30 000 N. And the direction of the moment, acted on the B inner surface, is on the x axis. The value of the moment is 60 Nm. There are four inclined holes in the structure, which are labeled C on the Figure 2 the initial model. These four inclined holes is used to install two shaft, in order to mounting two oil cylinder on this structure. So there are forces, acted on the label C circular surface. The value of these forces are -10 000 N on the x direction and -30 000 N on the direction of the z axis[3].

The structural static analysis[3]is used for the original model. According to the condition of the loading, the von Mises stress[4]of the initial model is calculated through the method of the finite element analysis, shown in Figure 3. The maximum value of the von Mises stress is 33 MPa.

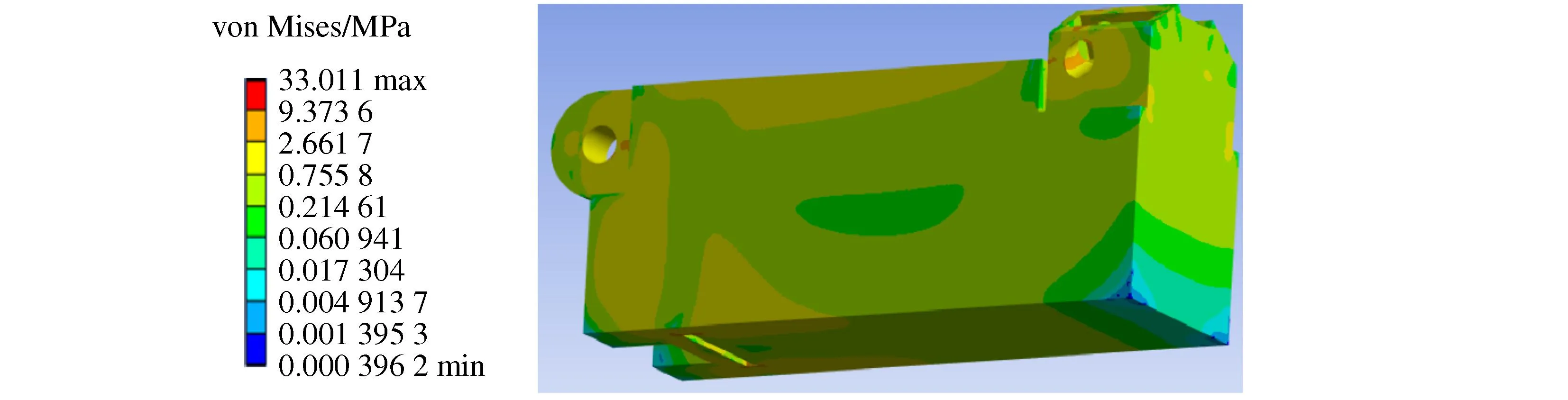
Figure 3 Original stress

Then structure topological optimization[3,5]is carried out. Click on objective underneath structural optimization in the outline tree. The compliance is chose for the static structural underneath the response type in the worksheet. Click on response constraint underneath structural optimization in the outline tree. In the details of "Response Constraint", the mass is chose for response. And the value 40% enter for the percent to retain.

The solution is retrieved to create an optimal shape. 40% mass is suggested for the design under the given loads as shown in Figure 4. While the front and back of the structure should be connected to the other structures, so as to form a complete working mechanism. This optimal structure makes it no possible. Because the back part of the optimal structure, the white circle area of the Figure 4, have no space to install the other one, which is used to support each other. So this result can not be applied to the real world. There is no need to continue with the forth step and the fifth step of the topology optimization process.

Next the parameter of the response constraint to retain mass[6], should be adjusted. The value of the parameter is reduced to 20%, the solution of the optimization see the Figure 5.

Figure 5 20% mass

Based on the structure optimization[6]of the 20% retain mass, the structure optimization model is created again and verified. The optimization structure is created according to the solution of the optimization simulation. And the loads acting on the optimization structure. The support location is same as the original position of the initial structure.

The method of the finite element analysis is used on the optimization structure. The result of the von Mises stress[2,7]is shown as Figure 6 the optimization structure stress. And the maximum von Mises stress is reduced to 15 MPa.

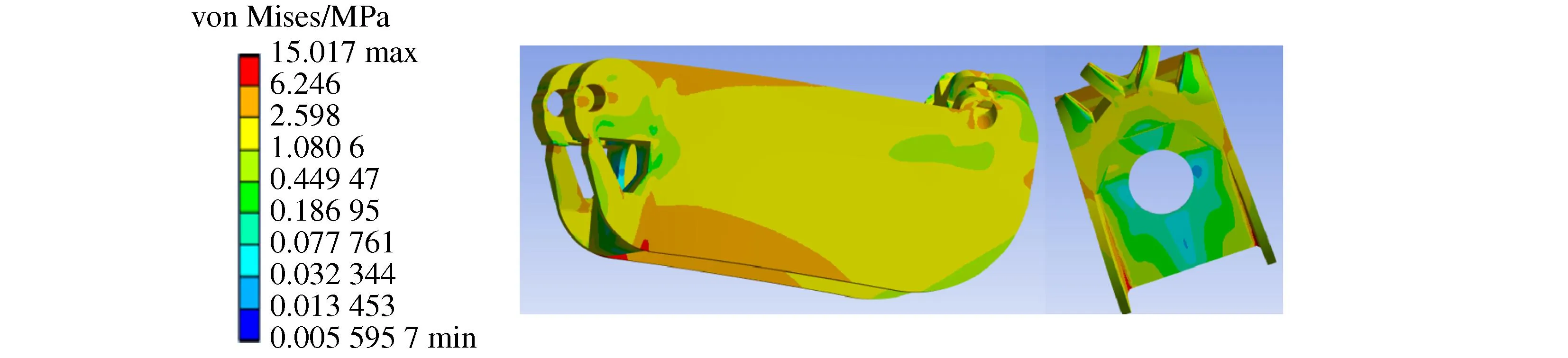
Figure 6 The optimization structure stress

3 Conclusion

The maximum von Mises stress of the initial structure model is 33 MPa. Through topology optimized twice, the mass retains 20% of the all weight. The topology optimization structure is created. Its maximum von Mises stress is 15 MPa. The two numbers are compared. The value of the optimization structure is less than the number of the initial structure. Any other values of the solution about statics analysis, are compared with the two different structure. So this topology optimization process is successful for the working arm.