一类恒成立问题的多解探究与思考*
2024-01-09福建省福清融城中学350300林世平
福建省福清融城中学 (350300) 林世平
福建省福清市教师进修学校 (350300) 林新建
不等式恒成立问题一直是高考热点之一,因其考查的视角宽、灵活多变而成为重点考查内容;这类问题有一定的难度,对学生的能力要求较高,更是各地高三模拟卷中压轴客观题的常客之一.本文以2023年2月福州市普通高中毕业班质量检测第22题中第二题的第一问为例,在充分挖掘图像特征的基础上,优化解题途径,通过一题多解的方式进行探究与思考.
1 问题呈现
例(2023年2月福州市普通高中毕业班质量检测第22题) 已知函数f(x)=(x+1)lnx-ax+a.
(1)若a=2时,试判断f(x)的单调性,并证明你的结论;
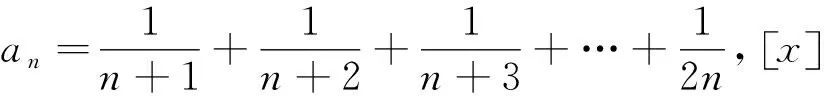
本题题干简练,又以我们熟悉的问题方式呈现,入口较宽,易于上手,且解法多样.在考查基础知识的同时,注重考查推理论证能力、运算求解能力,突出考查数学理性思维以及对数学本质的理解,着重考查化归与转化思想、数形结合思想和逻辑推理、数学运算等核心素养.
2 解法探析


(1)当2-a≥0,即a≤2时,得f′(x)≥0,故f(x)递增,则f(x)min=f(1)=0,即当x>1时,f(x)>0恒成立.
(2)当2-a<0,即a>2时,得f′(x)<0,说明f′(x)由负到正,则不妨令x=x0时,f′(x0)=0,可知当1
综上所述,a的取值范围为a≤2.

上述两种方法均是按照常规套路分析,在分类讨论中又要虚设零点进行计算,这无形增加了我们的思想负担;而分离参数后,要用到更为陌生的洛必达法则求解,显然更不容易解决问题.其实在求导之前,我们先从“直观上”探析题设条件,就会有意外惊喜.
直观之一:当x>1时,f(x)>0恒成立;即函数f(x)在(1,+∞)上的图像位于x轴的上方(可以与x轴有交点,又x=1时,f(1)=0),只是此时函数f(x)的图像不容易画出来.
直观之二:进一步感知f(x)>0,实际上就是(x+1)lnx>ax-a恒成立,而且它们的零点均是1,函数y=(x+1)lnx与y=a(x-1)的图像在相切时取最值.
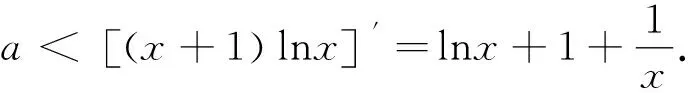
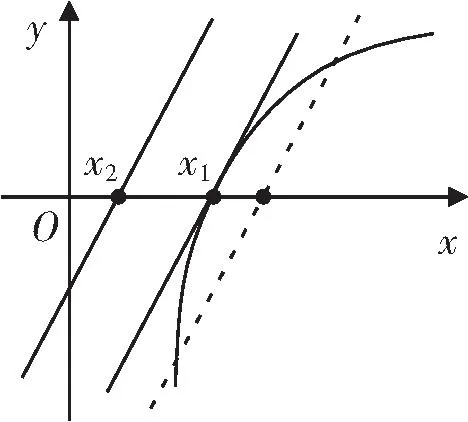
解法4:(切线放缩)由x>1时,f(x)>0恒成立,实际上就是(x+1)lnx>ax-a恒成立,由解法3可知,左右两函数刚好在(1,0)相切.易证得当x≥1时,(x-1)≥lnx,故当a>0时,(x+1)lnx>a(x-1)≥alnx.因为x>1,lnx>0, 则(x+1)>a,求得a的取值范围为0 评析:本题属于一类不等式恒成立问题,经常以考查参数的取值形式出现,主要考查学生的理性思维以及数形结合、化归与转化思想,着重考查逻辑推理和数学运算等核心素养. 由上述探究可以发现,这类可转化成ax+b≤f(x)(一般为凹函数)或ax+b≥f(x)(常为凸函数)的恒成立问题,只要我们能够根据数形结合思想,直观图像的特征,挖掘其性质,就可优化解决问题的途径.如,不等式ax+b≤f(x)恒成立(如图1),即曲线恒在直线的上方;不等式ax+b≥f(x)恒成立(如图2),就是直线恒在曲线的上方. 当直线y=ax+b与x轴交点在曲线包围的区域中时,是不可能存在实数a,b满足恒成立要求的,如图1、2中虚线所示. 图1 图2 直观分析图像特征,发现问题还可化为函数y=f(x)(具有凹凸性)和y=ax+b的两个零点大小比较,这样就可以轻松解决问题;显然等号成立时,是处于零点的相切状态.倘若曲线函数无零点时,就可转化为相切类型求解. 不等式恒成立的求参问题往往让学生望而生畏,尤其是较为复杂不等式,在化简过程中经常出现问题,使得学生一碰到不等式问题就没有信心去解决问题.因此教学中要多探究新的方法,简便的方法,重树解决问题的自信心. (1)求f(x)的解析式及单调区间; 直观之一:要使ex≥(a+1)x+b恒成立,必须(a+1)>0,要使(a+1)b最大,须b>0. 直观之二:画出图象,如图3,可直观感知,函数y=ex与y=(a+1)x+b的图像必须相切.从而明确了为何题设中给出的已知函数与所求问题的关系,探求到问题的本质,进而快捷解决问题. 图3 解决相对比较复杂的函数的性质问题时应先直观分析函数结构特点,转化为比较熟悉的函数间的关系,再画出函数的图像,将函数的性质问题转化成图像之间的相交或度量关系等问题,以探清问题的本质,从而轻松解决问题.若问题给出的函数无法离析出几个简单函数间的关系,则再考虑用含参讨论或分离参数的方法解决问题.教师在课堂教学中一定要坚持素养导向、能力并重的原则,加强培养学生的应用意识和创新意识,提升学生的思维灵活性,发展学生的核心素养.3 感悟反思

4 应用赏析
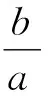
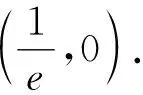

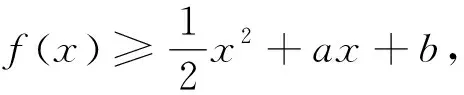


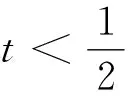
5.结语
