例析线段调和分割背景下的圆锥曲线问题

浙江省衢州第二中学 (324000) 万 祺

浙江省衢州市教育局教研室 (324000) 叶水爱

调和点列是射影几何中的重要内容,本文阐述圆锥曲线中的调和分割及其简单性质,并探寻一类以此为背景的圆锥曲线问题的命题依据.

1 调和分割的定义及性质

1.2 线段调和分割的性质:如图1,点C,D调和分割线段AB的充要条件是满足如下条件之一:

图1

(1)点A,B调和分割线段CD;

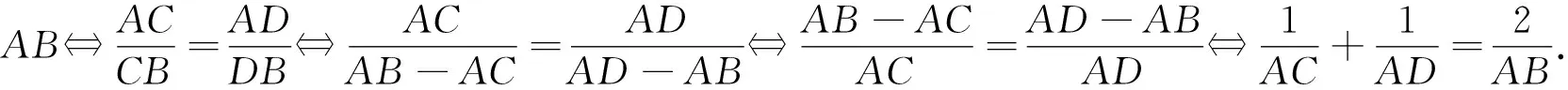
1.3 调和线束的定义:如图2,若直线l上四点A,C,B,D是调和点列,过直线l外一点P,分别引射线PA,PC,PB,PD,则PA,PC,PB,PD是一簇调和线束.

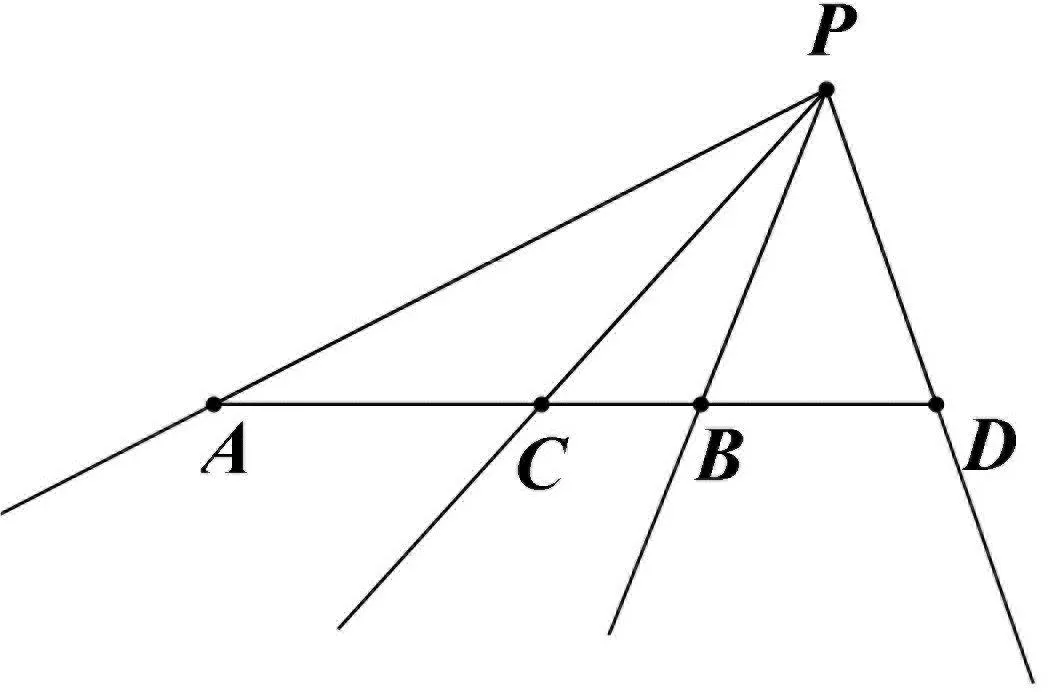
图2

1.4 调和线束的性质:若PA,PC,PB,PD是一簇调和线束,(1)如图3,不同于直线l的直线m分别交直线PA,PC,PB,PD于点A′,C′,B′,D′,则A′,C′,B′,D′成调和点列;

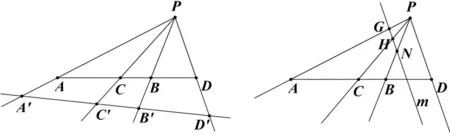
图3 图4

(2)若直线m与PA,PC,PB,PD之一平行,则m被其他三条直线截成相等的两段(如图4,m//PD,且m分别交PA,PC,PB于点G,H,N,则HG=HN,事实上性质(2)是性质(1)的特例,即G,H,N,Q成调和点列,这里Q在直线GN上的无穷远处);

(3)PC平分∠APB当且仅当PC⊥PD.

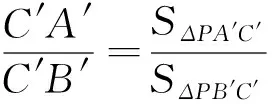
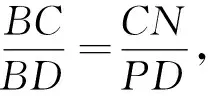
(3)过C作GN//PD,交PA,PB于点G,N,由性质(2)可知CN=CG,结合∠APC=∠BPC知PC⊥GN,故PC⊥PD;反之由PC⊥PD亦可推出∠APC=∠BPC,故命题成立.

2 圆锥曲线中的调和点列

若点P和直线l是圆锥曲线Γ的一对极点和极线(P不在曲线Γ上且不是曲线Γ的中心),过P作一直线交Γ于M,N两点,交直线l于点H,则P,H调和分割MN.

下面以椭圆为例,给出证明.

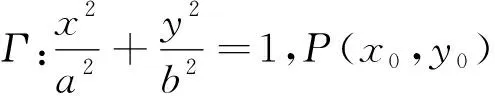
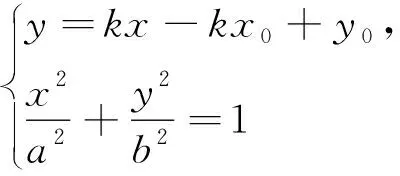
3 真题探析

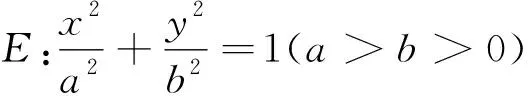
(1)求椭圆E的方程;

(2)过点P(-2,1)作斜率为k的直线与椭圆E交于不同的两点B,C,直线AB,AC分别与x轴交于点M,N,当|MN|=2时,求k的值．

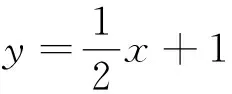
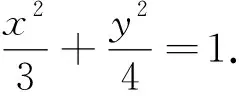
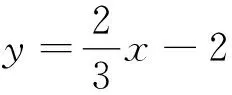
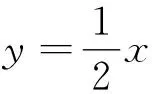
简析:(1)易得斜率k∈(-∞,-3)∪(-3,0)∪(0,1).

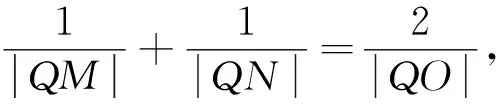
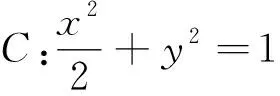
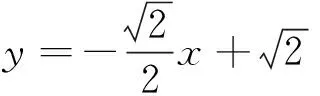
(2)点F(1,0)的极线m方程为x=2,记AB∩m=G,则F,G调和分割AB,故MA,MF,MB,MG成调和线束,又MF⊥MG,由调和线束性质(3)知MF平分∠AMB,即∠OMA=∠OMB.

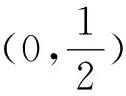
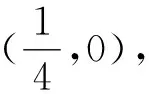
4 应用举例

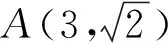
(1)求双曲线C的标准方程;

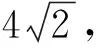
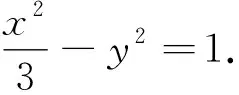
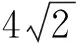
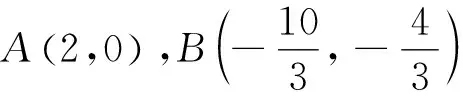
5 结语

波利亚曾说:“我们熟悉题目要注意题目条件和问题背景,解完题目后要注意回顾.”事实上,数学问题的解决只是解题的一部分,更重要的是探寻题目的背景与内涵,进一步提炼数学思想方法,并将其联系起来,推动思维发展.