回归定义 选择优化 联想类比--一道三角形周长最值问题的探究与变式

江苏省海门中学 (226100) 张 婕

本文从一道解三角形周长最值问题出发,分析如何帮助学生转化问题的难点,从哪些角度对问题进行深入的思考探究.

1.题目

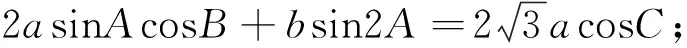
从三个条件中任选一个,补充在下面的问题中,并解答.

问题:在△ABC中,角A,B,C所对的边分别为a,b,c,满足:________.

(1)求角C的大小;

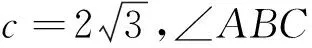
注:如果选择多个条件分别作答,按第一个解答计分.

本题采用结构不良,考查学生对三个条件的选择与优化.第(2)小问在已知条件上有所创新,需要学生分析其中的关系,进而构建数学模型,同时设问是求三角形周长的最值,考查学生对于解题方法的选择与优化.

2.解题思路

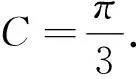
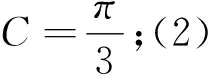
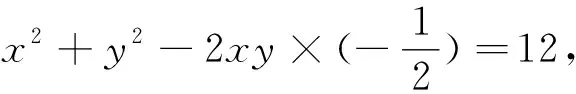
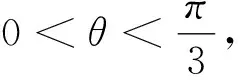
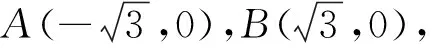
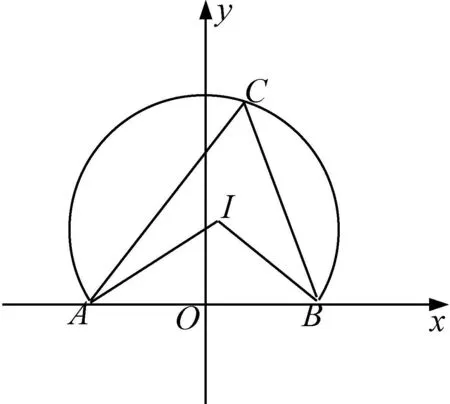
图1

3.思考探究

面对原问题,从哪些角度提出新的问题,背后反映出来的是学生的数学思维方法的运用.所谓创新,就是在微小的地方做改变,因此在教学过程中,教师要学会运用数学思维引导学生进行微探究,提出新问题.

思考1:(1)问题(2)中求△ABI周长的最值,运用类比思想,能否求△ABI周长的取值范围呢?

(2)问题(2)中求△ABI周长的最值,同样运用类比,能否求△ABI面积的最值和取值范围呢?

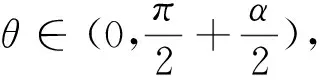
对于最值问题的解决,选择基本不等式求解来的更省时高效,对于周长的取值范围问题,一般选择设变量,构造函数将问题转化为求函数的值域.

思考2:由法三,可知点I在圆弧x2+(y+1)2=4(y>0)上,点C在圆弧x2+(y-1)2=4(y>0)上,因此若D为边AB上一点,且满足AD=2DB,则DI存在最小值,因此可得:

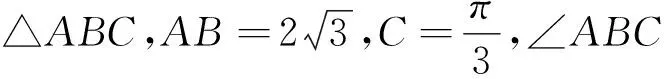
思考3:运用类比,改变问题的已知条件,若G为CA,CB两条边上中线的交点,能否求△ABG的周长与面积的最值和取值范围呢?

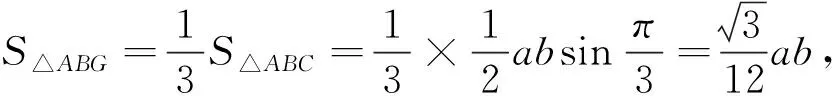
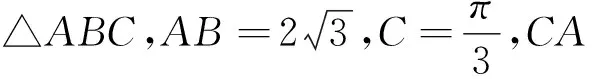
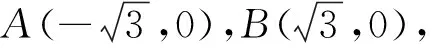
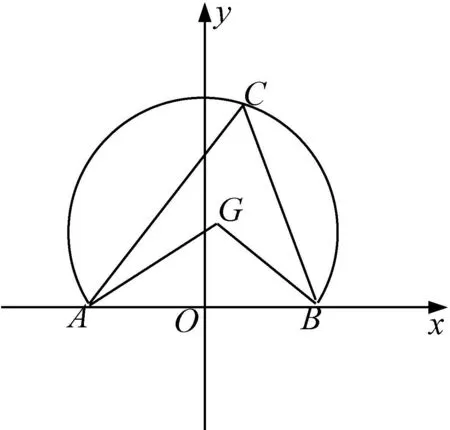
图2

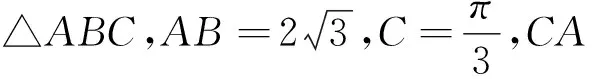
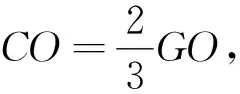
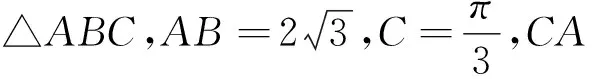
思考4:再次运用类比想法,若H为CA,CB两条边上高的交点,能否求△ABH的周长与面积的最值和取值范围呢?

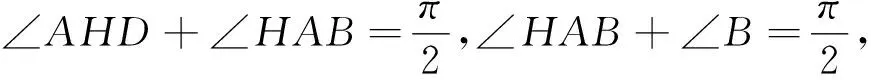
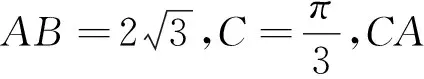
进一步,若CA,CB边的中垂线交于点O,此时O为△ABC的外心,△ABO的面积和周长均为定值.

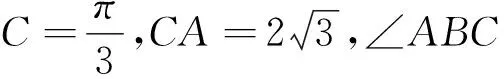
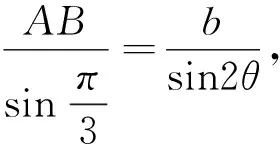
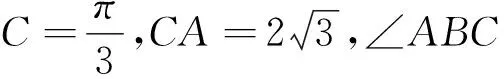
当然,运用类比的思维还可以在原问题的基础上提出更多的问题,限于篇幅,不再赘述.

4.结语

一道让学生感到困难的问题,对于课堂教学来说,就是一个宝藏.它能反映出学生的思维障碍,教师要做的就是创设桥梁让学生突破障碍、掌握方法.它能帮助学生积累数学探究的经验,对某个条件或问题进行变换,就是给学生创造探究的机会,提升学生探究的意识,从而促进学生数学探究能力的提升.