“拾级而上”巧设问 “固本溯源”求本质*

浙江省绍兴市越州中学 (312075) 张 颖 何建东

问题解决是数学教学的核心和灵魂,分析、解决问题的过程是数学教学中师生交流的重要载体．而如何有效地设计问题链以引起学生的思考,是保证课堂教学有效性的基础和关键．新课程、新教材、新高考(“三新”)背景下,数学教师通过巧妙设计问题来引导学生思考,通过探求知识本质来促进学生思维,最终达到发展学生核心素养的目的．本文结合笔者在“数列通项”专题复习教学实践,设计了“基础型、发展型、拓展型”三种层次的问题链,在此基础上对相关知识的内涵与外延进行更本质的梳理与概括．

1 “明晰内容”细解析

《普通高中数学课程标准(2017年版2020年修订)》对数列内容教学定位是:探索并掌握等差数列和等比数列的变化规律,建立通项公式和前n项和公式;能运用等差数列、等比数列解决简单的实际问题和数学问题,感受数学模型的现实意义与应用;了解等差数列与一元一次函数、等比数列与指数函数的联系,感受数列与函数的共性与差异,体会数学的整体性;能在具体的问题情境中,发现数列的等差关系和等比关系,并解决相应的问题．

正因为数列问题的分析与解决可以考查学生的逻辑推理、数学运算、数据分析等多种核心素养,是新高考的重要内容.数列问题除了考查等差数列和等比数列两种最特殊最基本数列的知识、概念与公式外,数列通项和数列求和是非常重要的两大问题类型,它们也是更高难度要求的分类讨论、数列放缩、数列与函数等其他内容结合的综合性问题的重要桥梁纽带．正因此,好的问题教学设计更能达到好的教学效果.

2 “拾级而上”巧设问

基于“三新”背景的高中数学教学更应侧重科学有效的问题链设计,根据数列通项的内容解析,笔者认为可以设计如下三种问题链:

(1) 基础型问题链,这类问题链侧重于基础知识检查巩固与基本方法尝试掌握.

问题1已知数列{an}满足a1=1,an+1=an+2,求an．(答案:an=2n-1)．

问题2已知数列{an}满足a1=1,an+1=2an,求an． (答案:an=2n-1)．

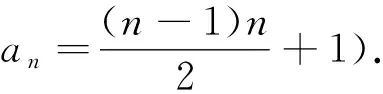
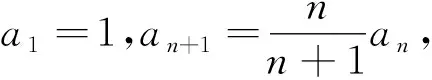
问题5 已知数列{an}的前n项和Sn=2n2+3n+1,a1=6,求an．

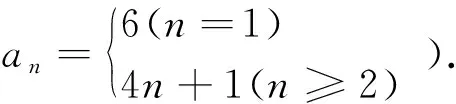
(2)发展型问题链,这类问题链侧重于基本能力适度提高与基本思想灵活运用.

问题7 已知数列{an}满足a1=1,an+1=2an+3,求数列{an}的通项公式．(答案:an=2n+1-3)．

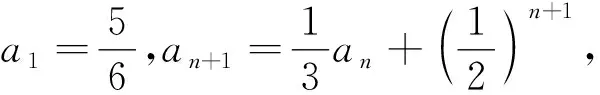
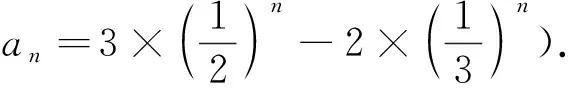
问题9 已知数列{an}满足a1= 1,an + 1= 10an2,求数列{an}的通项公式．

(答案:an=102n-1-1)．

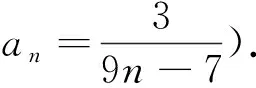
(3)拓展型问题链,这类问题链侧重于发展理科高阶思维与拓展强化核心素养．

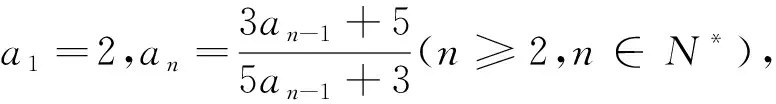
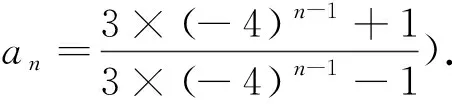
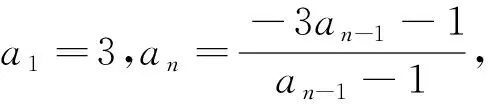
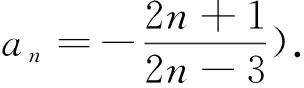
问题13 已知数列{an}满足a1=a2=5,且an+1=an+6an-1,求数列{an}的通项公式．

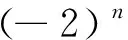
问题14已知数列{an}满足a1=1,a2=6,an+1=4an-4an-1,求数列{an}的通项公式．

(答案:an=n·2n-2n-1)．

3 “固本溯源”求本质

数列通项的求解由易及难,从知识、方法到能力、思想,再到思维、素养,可以进行探求,形成系列.

(1)定义法:形如an+1=an+m或an+1=man(n∈N+下同,m为常数),可根据定义判定为等差数列或等比数列,然后直接利用定义求得通项．

(2)累加法:形如an+1=an+f(n),可利用累加法消去等号两侧相同的项,得到通项．

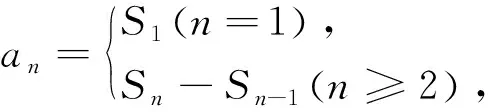
(5)待定系数法:某些特别形式的递推关系可以通过待定系数法,将数列关系转化为整体的等差或等比数列,进行求解,常见题型有:

题型一an+1=pan+q(p,q均为常数且pq(1-p)≠0)．

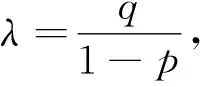
题型二an+1=pan+rεn(p,q,r为常数,pqr≠0且p≠q)．

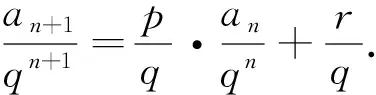
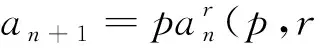
处理方法:等式左右两边同时取常用对数得lgan + 1= lg(panr) = lgp+rlgan,令bn=lgan,m=lgp,则bn+1=rbn+m(m,r为实数且mr(1-r)≠0)即变为形式一,再用待定系数法处理．

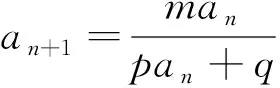
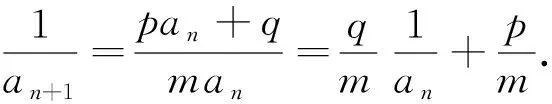
(7)特征根法:形如an+1=pan+qan-1(p,q为常数)的数列通项问题可以用特征根法进行求解,其特征根方程为x2=px+q,即x2-px-q=0．