从一题多解到多题一解--由一道高考题引发的思考

江苏省常州高级中学 (213003) 李泊明

为了更好地备考,笔者认为我们要研读课程标准、高考评价体系,并以高考真题为重要载体研究高考,并把高考的要求落实到平时的复习中去,切实提高学生的核心素养.本文以新高考I卷第18题为例,提出笔者对解三角形一轮复习的一些思考.

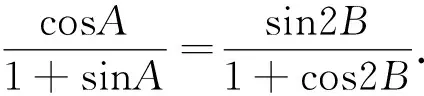
点评:本题是一道典型的解三角形综合题,涉及到的知识点很多,有诱导公式、两角和差公式、二倍角公式、正弦定理、基本不等式等,深度考查了考生的分析问题、解决问题能力.其中第(2)问思路较为狭窄,需要考生突破思维定势,果断利用正弦定理化边为角,再利用第(1)问中推出的C、B两角之间的关系消元.

分析完高考真题,笔者在今年的高三一轮复习解三角形模块中进行了如下的从一题多解到多题一解的问题链设计,供大家参考.

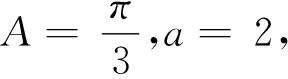
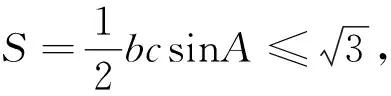
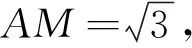
对于以上三种解法,解法1利用余弦定理化角为边,得到关于b,c的等式,再利用基本不等式直接得出bc的最大值,简洁明了;解法2利用正弦定理化边为角,再利用三角恒等变换将目标化为单变量B的函数,进而求得结果.这对三角恒等变形要求较高,但解法2的好处是,当对△ABC的形状再加一些限制时,我们很容易由B的精确范围得到△ABC面积的更精细的范围;解法3固定B、C两点,得到A点的轨迹,再利用几何直观得到△ABC面积的最大值,可以说计算量最小,但因为用到几何直观,更适合客观题.

为了更好地体会以上一题多解之间的优劣以及适用情形,在详细分析完例1后,给出了下面的一系列变式题.

分析:由于是求S的取值范围,最优的做法是利用正弦定理化边为角,再消元得到单变量的函数.

分析:由于是求S的取值范围,并且还有锐角三角形的限制.最优的做法还是利用正弦定理化边为角,再消元得到单变量的函数.

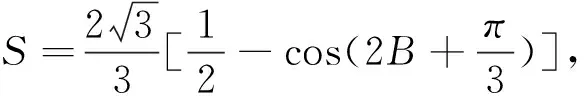
分析:l=2+b+c,只要求b+c最大值,最优的解法是由余弦定理化角为边,利用基本不等式求最值.

分析:由于是求l的取值范围,并且还有锐角三角形的限制.最优的做法还是利用正弦定理化边为角,再消元得到单变量的函数.

分析:若用余弦定理得到4=b2+c2-bc,再求b+2c的最大值需构造不等式,这有一定技巧,而如果用正弦定理化边为角就没有难度了.

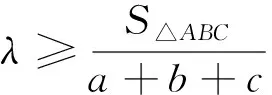
点评:以上6个变式将已知三角形的一角及其对边这一经典模型讨论的非常充分了,通过分析,我们对于正弦定理、余弦定理的使用和选择认识更加深刻了.但实际解题中,我们会碰到很多有别于以上经典模型的题目,我们又该如何选择合适的方法呢?

于是笔者又设计了以下的两个例题.

点评:思路一可行,但运算量明显大,实际解题时应该回避,选择思路二.

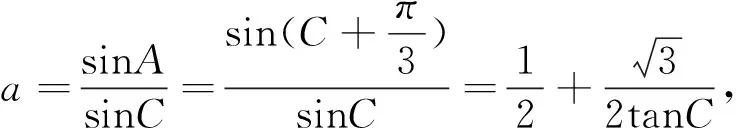
点评:思路一和思路二运算量差不多,但思路二目标更明确,刻画锐角三角形更简单,是解三角形中求取值范围问题的通法.

结束语解三角形是高考的重要考点,解三角的题目又灵活多变.一个三角形,角有三个,边有三条,每个角又有三个三角函数值,既有正弦定理,又有余弦定理,还有几何直观,面积还有很多表达形式,三角恒等变换的公式等．教师要精选例题,通过一题多解让学生掌握解决问题的常见思想方法.并且通过辨析多种解法的优劣,引导学生根据具体问题的个性化结构,全方位、多角度地观察和分析问题,让学生抓住问题的关键,明确问题的核心.还要从一题多解过渡到多题一解,掌握不同问题的通性通法,追求一般的思维方式,挖掘方法背后的思想,发挥思想的统领作用, 最终使学生能够从数学思想方法的视角出发,分析和解决问题,并使之成为学生思考和解决问题的一种自觉习惯.