再议“齐次化”方法解决定点定值问题

浙江省宁波市第四中学 (315016) 蒋亚军

定值定点问题是解析几何中的典型问题,不仅是各类模考题的热点,也是高考题的高频考点,是学生既熟悉又头疼的问题,熟悉在于平时经常会遇见,头疼在于有思路没答案、会而不对.在文[1]中有过介绍,对圆锥曲线上一定点M(x0,y0)和两动点A,B(异于点M),已知动直线l过定点,求kMA+kMB或kMA·kMB为定值,已知kMA+kMB或kMA·kMB为定值求动直线l过定点.即定点求定值和定值找定点两种不同类型.“齐次化”是解决围绕着斜率和(积)为定值直线过定点的一种优化通法.

1 直接利用“齐次化”

评注:解析几何中的定点定值问题,利用“齐次化”的方法是一种降低思维难度优化数学运算的通性通法.其本质是整体代换的思想设目标斜率式的直线方程,将圆锥曲线的方程转化为关于斜率的一元二次方程,从而直接利用韦达定理处理斜率之积(和)为定值的问题[2].

2 转化后用“齐次化”

图1

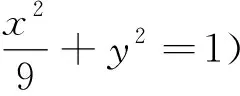
(2)证明:直线CD过定点.

3 对“齐次化”再认识

例4 如图2,过抛物线E:x2=4y上的点A(2,1)作斜率分别为k1,k2的直线,分别交抛物线E于B,C两点.若k1+k2=k1k2,证明:直线BC过定点.

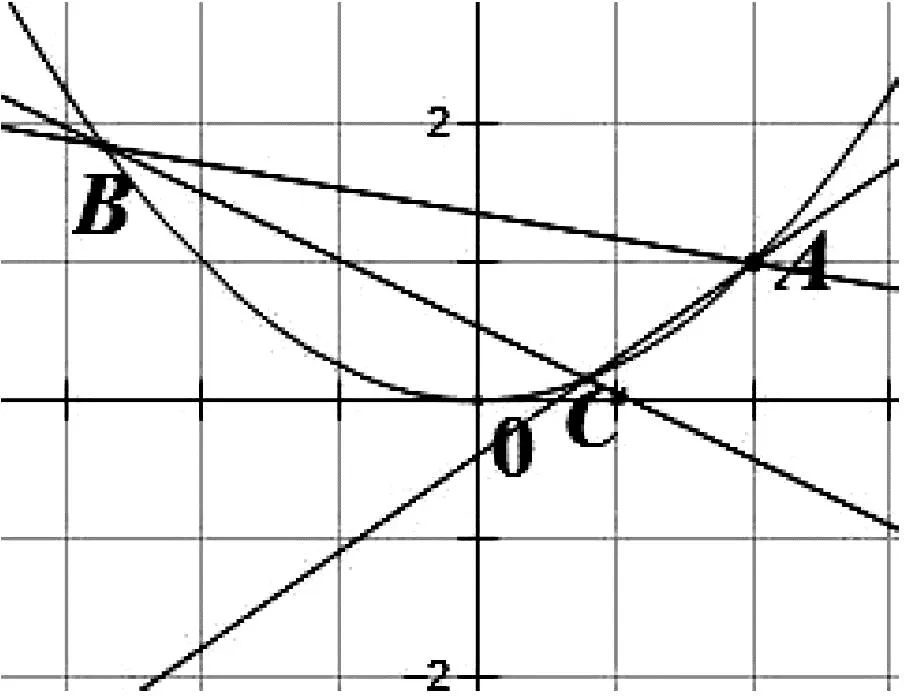
图2

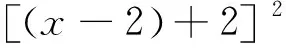
证明:设直线CD:m(x-2)+ny=1,代入

4 总结与反思

解析几何蕴含着丰富的数学思想,是落实学生数学运算素养的重要载体.通过对“齐次化”的学习和再认识,学生不仅学会利用“齐次化”解决的定点定值模型,而且还掌握利用“齐次化”解决“双斜率问题”的常见变形的方法,挖掘题干条件(隐含),构造目标式的齐二次方程. “齐次化”的方法对解决定点定值引发的双斜率问题,可以起到降低思维难度、简化运算的效果.在教学中要回归知识本质,强化通性通法,体会思维过程,着眼素养提升.