四新高考背景下一道质检试题赏析

福建省泉州市第七中学 (362000) 吴宝树

近年来,随着新高考综合改革工作的推行,各地迎来了“四新”高考,也就是新高考方案、新课程标准、新课程方案、新高考教材．《普通高中数学课程标准(2017年版2020年修订)》指出数学教育帮助学生掌握现代生活和进一步学习所必需的数学知识、技能、思想和方法;提升学生的数学素养,引导学生会用数学眼光观察世界,会用数学思维思考世界,会用数学语言表达世界;数学学科核心素养是数学课程目标的集中体现,是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现,是在数学学习和应用的过程中逐步形成和发展的.数学学科核心素养包括:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.这些数学学科核心素养既相对独立、又相互交融,是一个有机的整体.自2020年起,考试大纲和考试说明取消,考生在备考时只能根据课程标准进行．课程标准更侧重能力和核心素质的培养和考查,考生也就面临着更多的新变化、新问题,整个高考形势都发生了变化,教师与考生面临着以往未曾遇到过的难题,因此课程标准下的命题研究已成为热点,各地的质检卷无疑是这一研究成果的很好的体现．本文以一道福建省质量监测试题为例,谈谈新课程背景下,如何深入挖掘质检试题价值,培养学生的数学核心素养的考查及一类问题的解答策略．

1．试题呈现

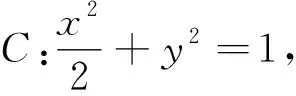
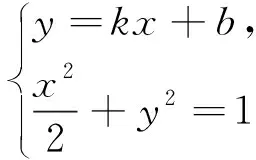
本题巧妙的糅合了椭圆和圆两种曲线,考查了数学抽象、 逻辑推理、直观想象、数学运算和数据分析等核心素养．解析几何的核心问题是用代数的方法处理几何问题．本题利用了“若圆O上一点Q的切线l1交椭圆C于点A,B,则OA⊥OB”这一几何关系来构造的.

探寻试题的背景及其背后的性质是试题研究的重要方法．那么本题中的这一几何关系在一般圆锥曲线中是否成立?

2.问题推广

将本题中的椭圆和圆一般化,可以得到一般性结论.

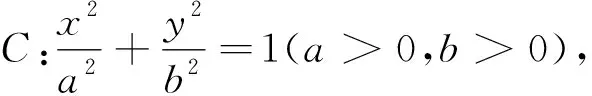
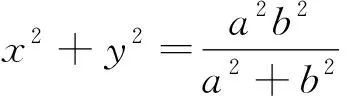
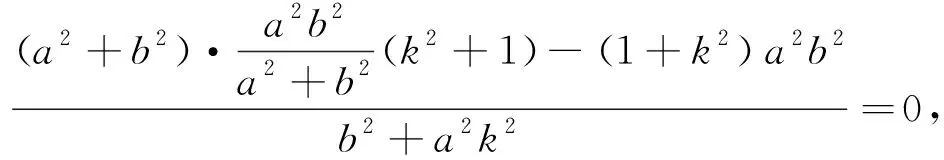
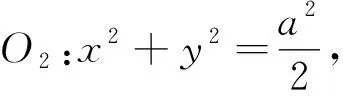
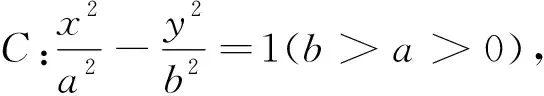
推广4 已知抛物线y2=2px(p>0),点圆O:(x-2p)2+y2=0上一动点M做点圆O的切线,该切线与抛物线C相交于A,B两点,则以AB为直径的圆过定点(0,0)．

3.尝试改编

基于以上一般性质,笔者尝试通过变换曲线类型、改变设问方式等形式,对这类试题进行适当改造,充分挖掘试题价值,举一反三.

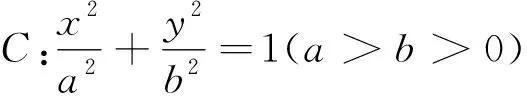
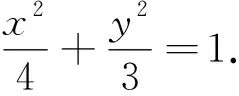
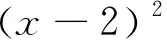
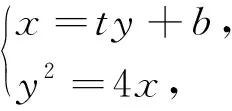
《普通高中数学课程标准(2017年版2020年修订)》中平面解析几何学业要求这部分指出:能够根据几何问题和图形的特点,用代数语言把几何问题转化成为代数问题;根据对几何问题 (图形)的分析,探索解决问题的思路;运用代数方法得到结论;给出代数结论合理的几何解释,解决几何问题.重点提升直观想象、数学运算、数学建模、逻辑推理和数学抽象素养.本文基于以上要求,以一道省适应性考试试题为例,阐述了在四新高考背景下,如何充分挖掘试题价值,考查学生核心素养,精准备考.